헤테로 접합

헤테로 접합은 서로 다른 반도체의 두 층 또는 영역 사이의 인터페이스입니다.이 반도체 재료들은 호모 접합과는 반대로 밴드 갭이 일정하지 않다.반도체 레이저, 태양전지 및 트랜지스터를 포함한 많은 솔리드 스테이트 디바이스 애플리케이션에서 전자 에너지 대역을 엔지니어링하는 것이 종종 유리합니다.디바이스에서 여러 개의 헤테로 접합을 조합하는 것을 헤테로 구조라고 부릅니다만, 이 두 용어는 일반적으로 서로 교환할 수 있습니다.각 재료가 동일하지 않은 밴드 갭을 가진 반도체여야 한다는 요건은 다소 느슨하다. 특히 전자적 특성이 공간적 특성에 따라 달라지는 작은 길이의 스케일에서는 더욱 그러하다.헤테로 접합의 보다 현대적인 정의는 금속, 절연, 고속 이온 전도체 및 반도체 재료의 결정 및 비정질 구조를 포함한 두 개의 고체 물질 사이의 인터페이스입니다.

제조 및 응용 프로그램

헤테로 접합 제조에서는 일반적으로 증착 두께를 정밀하게 제어하고 깔끔하게 격자 매칭된 갑작스러운 인터페이스를 만들기 위해 분자선 에피택시(MBE)^[1] 또는 화학증착(CVD) 기술을 사용해야 합니다.최근 연구 중인 대안은 적층된 재료를 반데르발스 헤테로 ^[2]구조로 기계적으로 쌓는 것입니다.

비용에도 불구하고, 헤테로 접합은 고유한 특성이 중요한 다양한 전문 애플리케이션에서 사용되고 있습니다.

태양전지:헤테로 접합은 일반적으로 태양전지의 결정성 실리콘 기판과 비정질 실리콘 패시베이션층의 계면을 통해 형성된다.HIT(Intelligent Thin-Layer) 태양전지 구조와의 헤테로 접합은 1983년에^[3] 처음 개발되어 Sanyo/Panasonic에 의해 상용화되었다.HIT 태양 전지는 현재 26.^[4]^[1]^[5]7%의 변환 효율로 가장 효율적인 단일 접합 실리콘 태양 전지의 기록을 보유하고 있습니다.
레이저: 레이저에 헤테로 접합을 사용하는 것은 1963년 이 분야의 저명한 과학자 Herbert Kroemer가 인구 반전이 헤테로 구조에 의해 크게 강화될 수 있다고 제안했을 때 처음 [6] 제안되었습니다.AlAs와 같은 두 개의 큰 밴드 갭 층 사이에 GaAs와 같은 작은 직접 밴드 갭 소재를 포함시킴으로써 캐리어를 구속할 수 있으므로 역치 전류가 낮은 실온에서 레이싱이 발생할 수 있습니다.헤테로 구조 제작의 재료 과학이 Kroemer의 아이디어를 따라잡는 데 오랜 시간이 걸렸지만, 지금은 업계 표준이 되었습니다.밴드 갭은 양자 우물 헤테로 구조의 양자 크기 효과를 이용하여 제어할 수 있다는 것이 나중에 밝혀졌다.또, 헤테로 구조는, 반도체 레이저에서의 사용에 있어서의 또 다른 큰 장점인, 계면에서 발생하는 인덱스 스텝의 도파로로 사용할 수 있다.CD, DVD 플레이어에 사용되는 반도체 다이오드 레이저와 광섬유 트랜시버는 다양한 III-V, II-VI 화합물 반도체의 교대로 층을 만들어 레이싱 헤테로 구조를 형성한다.
바이폴라 트랜지스터:헤테로 접합을 바이폴라 접합 트랜지스터의 베이스-이미터 접합으로 사용하면 포워드 게인이 매우 높고 리버스 게인이 낮습니다.즉, 매우 양호한 고주파 동작(수십~수백 GHz의 값)과 낮은 누설 전류로 해석됩니다.이 소자는 헤테로 접합 바이폴라 트랜지스터(HBT)라고 불립니다.
전계효과 트랜지스터:헤테로 접합은 상당히 높은 주파수(500GHz 이상)로 동작할 수 있는 HEMT(High Electron Mobility Transistor)에 사용됩니다.적절한 도핑 프로파일과 밴드 얼라인먼트는 산란이 거의 발생하지 않는 도판트 프리 영역 내에 2차원 전자 가스를 생성함으로써 매우 높은 전자 이동성을 발생시킵니다.

에너지 밴드 얼라인먼트

밴드 얼라인먼트에 의해 정리된 세 가지 유형의 반도체 헤테로 접합.

평형에서의 n-n 반도체 헤테로 접합에 대한 밴드 다이어그램.

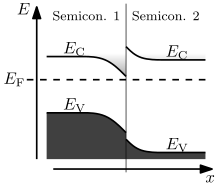
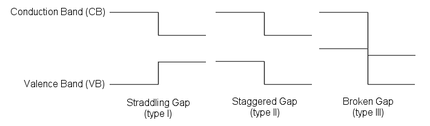
반도체 접합부의 동작은 인터페이스에서의 에너지 대역의 정렬에 의해 결정적으로 좌우됩니다.반도체 인터페이스는 ^[7]그림과 같이 스트래들링 갭(타입 I), 시차 갭(타입 II) 또는 파손 갭(타입 III)의 3가지 유형의 헤테로 접합으로 구성할 수 있습니다.밴드 벤딩은 접합부를 벗어나 포아송 방정식을 푸는 일반적인 절차에 따라 계산할 수 있습니다.

밴드 정렬을 예측하기 위해 다양한 모델이 존재합니다.

가장 간단한(그리고 정확도가 낮은) 모델은 Anderson의 법칙으로, 진공-반도체 계면의 특성(특히 진공 전자 친화성)에 기초하여 밴드 정렬을 예측합니다.주된 한계는 화학적 결합을 소홀히 한다는 것이다.
음이온 밴드가 음이온 상태와 관련이 있기 때문에 음이온이 동일한 재료는 매우 작은 양의 음이온 밴드 오프셋을 가져야 한다고 추측하는 공통 음이온 규칙이 제안되었습니다.그러나 이는 데이터를 설명하지는 못했지만 음이온이 다른 두 물질이 전도 대역 오프셋보다 더 큰 원자가 대역 오프셋을 갖는 경향과 관련이 있다.
Tersoff는^[8] 숏키 장벽 높이의 차이로 전도 대역 오프셋이 주어지는 보다 친숙한 금속-반도체 접합에 기초한 갭 상태 모델을 제안했다.이 모델은 한 물질의 전도 대역에서 다른 물질의 갭으로 전자 터널링에서 발생하는 두 반도체 사이의 계면에 쌍극자 층을 포함한다(금속 유도 갭 상태와 유사).이 모델은 GaAs/AlGaAs와 같이 두 소재가 격자 형태로^[9] 밀접하게 일치하는 시스템과 잘 어울립니다.
60:40 법칙은 반도체 GaAs와 합금 반도체 AlGaAs_x_1−x 사이의 접합에 대한 특정 사례에 대한 휴리스틱입니다.AlGaAs측의_x_1−x x가 0 ~1로 변화하고 있기 때문에, $\Delta E_{C}/\Delta E_{V}$ E $\Delta E_{C}/\Delta E_{V}$ / $\Delta E_{C}/\Delta E_{V}$ $\Delta E_{C}/\Delta E_{V}$ V \ $displaystyle$ \ $Delta E_{C}/\ Delta E_{V}$ 의 $\Delta E_C/\Delta E_V$ 비율은 60/40을 유지하는 경향이 있습니다.비교를 위해 Anderson의 규칙은 GaAs/Alas 접합부(x=^[10]^[11]1)에 대해 $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ E $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ / $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ V $=$ / $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ . $\Delta E_{C}/\Delta E_{V}=0.73/0.27$ ${displaystyle \Delta E_{C}/\Delta E_{V$ }= $0.73/0.27}$ 을 $\Delta E_C / \Delta E_V = 0.73/0.27$ 예측합니다.

밴드 오프셋을 측정하는 일반적인 방법은 발광 ^[11]스펙트럼의 여기자 에너지 측정에서 밴드 오프셋을 계산하는 것이다.

유효 질량 불일치

서로 다른 두 개의 반도체에 의해 헤테로 접합이 형성되면 밴드 구조의 차이로 양자 웰을 제작할 수 있다.달성된 양자 우물 내의 정적 에너지 레벨을 계산하기 위해, 헤테로 접합에 걸친 유효 질량의 변화 또는 불일치를 이해하는 것이 상당해진다.헤테로 접합에 정의된 양자 우물은 l $l_{w}$ 의 $폭을 갖는$ 유한 우물 전위로 취급할 수 있다 $l_{w}$ 또한 1966년 콘리 등 ^[12]및 벤다니엘과^[13] 듀크는 벤다니엘로 알려진 양자 우물의 외피 함수에 대한 경계 조건을 보고했다.듀크 경계 조건.이에 따르면 가공된 양자우물의 외피함수는 $)\style$ \ $psi(z)}$ 와 $\psi (z)$ 1m $∗$ z ${\frac {1}{m^{*}}}{\partial \over {\partial z}}\psi (z)\,$ z $)\$ {1 $}{m^{*}{\partial$ z $}}\$ psi( $z$ 가 모두 연속된 경계조건을 만족해야 $한다.$

양자 우물 예제를 위해 수학적 세부 사항이 적용되었습니다.

폭이 $l_{w}$ {\ $displaystyle l_{w}}$ 이고 $l_w$ 중심이 0인 유한 웰에 대한 슈뢰딩거 방정식을 사용하면 달성된 양자 웰에 대한 방정식을 다음과 같이 쓸 수 있습니다.

{\displaystyle - {\frac ^{2}}{2m_{b}^{*}{\frac {mathrm {d}^{2}\psi(z)}{\mathrm {d}z^{2}}+V\psi(z)=E\psi (z)\quad \quad {}z <-{\frac {l_{w}}{2}}\quad \quad (1)

\displaystyle \text - {\frac ^{2} {2m_{w}^{*}}{\frac {mathrm {d}^{2}\psi(z)}=E\psi(z)\text{}-{\frac {l}{w}}{\frac {\w}}{\frcl}{{\frc}}}}{{{{\frc}}}}}}}}{\mathrac {\mathrc}}}}}{{{{{\c

- {\frac ^{2}}{2m_{b}^{*}{\frac {mathrm {d}^{2}\psi(z)}{\mathrm {d}z^{2}}+V\psi(z)=E\psi (z)\quad {}z}+{\frac {l_{w}}{2}\quad \quad (3)

위의 방정식에 대한 해법은 k( $\kappa$ )와 k $({displaystyle \kappa})$ 만 있는 것으로 알려져 있습니다.

k

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

폭

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

b (

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

-

k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(V-E)}}{\hbar }}\quad \quad (4)

)

ℏ

4

（

4 ）{

display

k =

display

k

=

display

frac

{ 2 m _ {

w }

} {\ hbar }

=

display

frac { 2 m

_

b

（ V - E ）

}

} \

hbar }

z $+{\frac {l_{w}}{2}}$ + $+{\frac {l_{w}}{2}}$ w $({$ { $l_{w}}{2}})$ 에서 $+ \frac {l_w} {2}$ 균등화 솔루션을 얻을 수 있습니다.

A\cos({\frac {kl_{w}}{2}})=B\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (5)

=

B\

exp

(-{\frac

{

kappa l_{w}}{2}})\syslog \exp

(5

A\cos({\frac {kl_{w}}{2}})=B\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (5)

(5)의 도함수를 구하여 ${\frac {1}{m^{*}}}$ 에 ${\frac {1}{m^{*}}}$ †({ $displaystyle {1}{m^{*}})$ 를 곱하면 된다.

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

A

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

（

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

2

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

） = -

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

m b

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

（ -

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

l w

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

) ( 6 )

-{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)

（

display

- { \

frac

{

kA

} {

m

_ { m _ { w

}^{

* } } } \ sin ( { \

frac

{ \

frac

{ w } { { { { { {

b

} {

b

} { b } { m } ) } ) ）

=

{ m }

(6)을 (5)로 나누면 짝수 패리티 솔루션 함수를 얻을 수 있다.

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

)

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

-

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

w

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

tan

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

(

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

w

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

) -

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

m

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

(

=

0 (

f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)

) {

display

f ( E ) = - { \

frac

{

k

} {

m

_ w }{ * } \

tan

\

frac

{

tan

_ {

w

} { { {

b

} } { \

frac

{\ frac { tan _ { w } } } } }

{\

frac {\

frac

} } } {\

frac

} { tan _ {

tan

_

w

} } } {

마찬가지로 홀수 패리티 솔루션의 경우

f

(

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

)

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

- k

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

cot

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

(

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

w

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

) +

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

m

f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)

0 (

8

)

=

- { \

frac

{ k } { m _ { w

}{

* } \ cots \

frac

{

cat

_ { w } {

b =

} * { \

frac

{

cat

_ { w } } }

수치 해법의 경우, (7)과 (8)의 도함수를 구하면 다음과 같이 된다.

짝수 패리티:

{\displaystyle\frac{df}{dE}}=sec frac {1}{*}{\frac {dk}{dE}}\tan({\frac {m_{w}}{2})+{\frac {k}{*}}\sec ^2}({\frac {w}{w}}}}{lc}}{\frac}}{\tan}}{\timesec}{frac}}{dk}}}}}}{frac}}{frac}}}{\frac}}}{\frac}}}}}}}{\frac}

홀수 패리티:

{\displaystyle\frac{df}{dE}}=flac {1}{m_{w}{*}}{\flac {dk}{dE}}\cot({\frac {kl_{w}}{2})-{\frac {k}{*}}\csc ^{2}({\frac {kl_{w}}{2})\times {l_{w}}{2}}{\frac {d}{d}}{d}}}{\ccc}E}}+{\frac {1}{m_{b}{*}}{\frac {d\kappa}{dE}}\quad \quad (9-2)}

${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ 서 d ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ d ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ m ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ 2 ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ d ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ - ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ m ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ 2 ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ - ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ ${\$ \ $displaystyle$ \ $frac$ { $dk$ } { $d$ $E}}$ = $flac {2m_{w}^*}$ { $2mrt {E}$ \ $hbar$ } } $\\$ \ $frac$ { $d\ kappa$ } { $dE$ } = - { \ $frac$ { $2m$ _ { $b$ } { 2m _ $b$ } } { $2mrcrt$ { V - $E$ } } } ${\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {V-E}}\hbar }}$ } } } } } $。$

재료 간 유효 질량의 차이는 지면 상태 에너지의 차이를 더 크게 만든다.

나노스케일 헤테로 접합

TEM으로 촬영한₃₄ 산화철(FeO-구)과 황화카드뮴(CdS-로드) 사이의 나노 크기의 헤테로 접합 이미지.이 엇갈린 간격(타입 II) 오프셋 접합은 2007년 어바나-샴페인 일리노이 대학의 Hunter McDaniel과 Moonsub Shim 박사에 의해 합성되었습니다.

양자 도트에서 밴드 에너지는 양자 크기 효과로 인해 결정 크기에 의존합니다.이를 통해 나노 크기의 헤테로 구조에서 밴드 오프셋 엔지니어링이 가능합니다.동일한 재료를 사용할 수 있지만^[15] 관련된 결정의 크기 또는 두께를 변경함으로써 예를 들어 접합부의 유형을 스트래들링(타입 I)에서 스태그드(타입 II)로 변경할 수 있다.가장 일반적인 나노 스케일 헤테로 구조 시스템은 가로 간격(타입 I) 오프셋을 가진 CdSe(CdSe@ZnS)의 ZnS입니다.본 발명의 시스템에서는 훨씬 큰 밴드갭 ZnS가 형광 CdSe 코어의 표면을 패시브화함으로써 발광의 양자 효율을 높인다.ZnS 쉘의 밴드 갭이 커짐에 따라 접착력이 강해지기 때문에 열 안정성이 향상됩니다.CdSe와 ZnS는 모두 아연블렌드 결정상에서 성장하며 격자적으로 밀접하게 일치하기 때문에 코어 셸 성장이 바람직하다.다른 시스템 또는 다른 성장 조건에서는 오른쪽 그림과 같은 이방성 구조를 성장시킬 수 있습니다.

이들 구조에서 전도대역 간 전하 전달의 원동력은 전도대역 오프셋인 것으로^[16] 나타났다.Robel ^[16]등은 TiO에서₂ 자라는 CdSe 나노결정 크기를 줄임으로써 전자가 높은 CdSe 전도 대역에서 TiO로₂ 더 빨리 전달된다는 것을 발견했다.CdSe에서 양자 크기 효과는 원자가 대역보다 유효 질량이 작기 때문에 전도 대역에서 훨씬 두드러지며, 대부분의 반도체가 그러하다.그 결과, 일반적으로 나노 크기의 헤테로 접합에 의해 전도 대역 오프셋의 엔지니어링이 훨씬 쉬워집니다.시차적(타입 II) 오프셋 나노스케일 헤테로 접합의 경우, 광유발 전하 분리가 발생할 수 있습니다. 왜냐하면 홀의 에너지 상태가 접합의 한쪽에 있는 반면 전자의 에너지 상태가 가장 낮기 때문입니다.광촉매, 특히 태양 에너지로 물을 쪼개기 위해 이방성 시차 간격(타입 II) 나노 크기의 헤테로 접합을 사용할 수 있다고 제안되어^[16] 왔다.

「」를 참조해 주세요.

Homojunction, p-n junction - 동일한 반도체의 두 가지 유형을 포함하는 접합입니다.
금속-반도체 접합: 금속과 반도체의 접합.

레퍼런스

^ ^a ^b 스미스, C.G(1996년)"저차원 양자 소자"프로그 의원신체 59(1996) 235282, 페이지 244.
^ Geim, A. K.; Grigorieva, I. V. (2013). "Van der Waals heterostructures". Nature. 499 (7459): 419–425. arXiv:1307.6718. doi:10.1038/nature12385. ISSN 0028-0836. PMID 23887427. S2CID 205234832.
^ Okuda, Koji; Okamoto, Hiroaki; Hamakawa, Yoshihiro (1983). "Amorphous Si/Polycrystalline Si Stacked Solar Cell Having More Than 12% Conversion Efficiency". Japanese Journal of Applied Physics. 22 (9): L605–L607. doi:10.1143/JJAP.22.L605.
^ Yamamoto, Kenji; Yoshikawa, Kunta; Uzu, Hisashi; Adachi, Daisuke (2018). "High-efficiency heterojunction crystalline Si solar cells". Japanese Journal of Applied Physics. 57 (8S3): 08RB20. doi:10.7567/JJAP.57.08RB20.
^ "HJT - Heterojunction Solar Cells". Solar Power Panels. Retrieved 2022-03-25.
^ Kroemer, H. (1963). "A proposed class of hetero-junction injection lasers". Proceedings of the IEEE. 51 (12): 1782–1783. doi:10.1109/PROC.1963.2706.
^ Ihn, Thomas (2010). "ch. 5.1 Band engineering". Semiconductor Nanostructures Quantum States and Electronic Transport. United States of America: Oxford University Press. pp. 66. ISBN 9780199534432.
^ J. Tersoff (1984). "Theory of semiconductor heterojunctions: The role of quantum dipoles". Physical Review B. 30 (8): 4874–4877. Bibcode:1984PhRvB..30.4874T. doi:10.1103/PhysRevB.30.4874.
^ 팔랍, 바타차랴(1997), 반도체 광전자 장치, 프렌티스 홀, ISBN 0-13-495656-7
^ Adachi, Sadao (1993-01-01). Properties of Aluminium Gallium Arsenide. ISBN 9780852965580.
^ ^a ^b Debbar, N.; Biswas, Dipankar; Bhattacharya, Pallab (1989). "Conduction-band offsets in pseudomorphic InxGa1-xAs/Al0.2Ga0.8As quantum wells (0.07≤x≤0.18) measured by deep-level transient spectroscopy". Physical Review B. 40 (2): 1058–1063. Bibcode:1989PhRvB..40.1058D. doi:10.1103/PhysRevB.40.1058. PMID 9991928.
^ Conley, J.; Duke, C.; Mahan, G.; Tiemann, J. (1966). "Electron Tunneling in Metal–Semiconductor Barriers". Physical Review. 150 (2): 466. Bibcode:1966PhRv..150..466C. doi:10.1103/PhysRev.150.466.
^ Bendaniel, D.; Duke, C. (1966). "Space-Charge Effects on Electron Tunneling". Physical Review. 152 (2): 683. Bibcode:1966PhRv..152..683B. doi:10.1103/PhysRev.152.683.
^ 그리피스, 데이비드 J. (2004)양자역학 입문 (제2판)프렌티스 홀.ISBN 0-13-11892-7
^ Ivanov, Sergei A.; Piryatinski, Andrei; Nanda, Jagjit; Tretiak, Sergei; Zavadil, Kevin R.; Wallace, William O.; Werder, Don; Klimov, Victor I. (2007). "Type-II Core/Shell CdS/ZnSe Nanocrystals: Synthesis, Electronic Structures, and Spectroscopic Properties". Journal of the American Chemical Society. 129 (38): 11708–19. doi:10.1021/ja068351m. PMID 17727285.
^ ^a ^b ^c Robel, István; Kuno, Masaru; Kamat, Prashant V. (2007). "Size-Dependent Electron Injection from Excited CdSe Quantum Dots into TiO2Nanoparticles". Journal of the American Chemical Society. 129 (14): 4136–7. doi:10.1021/ja070099a. PMID 17373799.

추가 정보

Bastard, Gérald (1991). Wave Mechanics Applied to Semiconductor Heterostructures. Wiley-Interscience. ISBN 978-0-470-21708-5.
Feucht, D. Lion; Milnes, A.G. (1970). Heterojunctions and metal–semiconductor junctions. New York City and London: Academic Press., ISBN 0-12-498050-3.응용 프로그램에 관한 다소 오래된 참고 자료이지만, 항상 헤테로 접합 장치의 기본 원리를 잘 소개합니다.
R. Tsu; F. Zypman (1990). "New insights in the physics of resonant tunneling". Surface Science. 228 (1–3): 418. Bibcode:1990SurSc.228..418T. doi:10.1016/0039-6028(90)90341-5.

[:0-1] 스미스, C.G(1996년)"저차원 양자 소자"프로그 의원신체 59(1996) 235282, 페이지 244.

[GeimGrigorieva2013-2] Geim, A. K.; Grigorieva, I. V. (2013). "Van der Waals heterostructures". Nature. 499 (7459): 419–425. arXiv:1307.6718. doi:10.1038/nature12385. ISSN 0028-0836. PMID 23887427. S2CID 205234832.

[3] Okuda, Koji; Okamoto, Hiroaki; Hamakawa, Yoshihiro (1983). "Amorphous Si/Polycrystalline Si Stacked Solar Cell Having More Than 12% Conversion Efficiency". Japanese Journal of Applied Physics. 22 (9): L605–L607. doi:10.1143/JJAP.22.L605.

[4] Yamamoto, Kenji; Yoshikawa, Kunta; Uzu, Hisashi; Adachi, Daisuke (2018). "High-efficiency heterojunction crystalline Si solar cells". Japanese Journal of Applied Physics. 57 (8S3): 08RB20. doi:10.7567/JJAP.57.08RB20.

[5] "HJT - Heterojunction Solar Cells". Solar Power Panels. Retrieved 2022-03-25.

[6] Kroemer, H. (1963). "A proposed class of hetero-junction injection lasers". Proceedings of the IEEE. 51 (12): 1782–1783. doi:10.1109/PROC.1963.2706.

[7] Ihn, Thomas (2010). "ch. 5.1 Band engineering". Semiconductor Nanostructures Quantum States and Electronic Transport. United States of America: Oxford University Press. pp. 66. ISBN 9780199534432.

[8] J. Tersoff (1984). "Theory of semiconductor heterojunctions: The role of quantum dipoles". Physical Review B. 30 (8): 4874–4877. Bibcode:1984PhRvB..30.4874T. doi:10.1103/PhysRevB.30.4874.

[pallab-9] 팔랍, 바타차랴(1997), 반도체 광전자 장치, 프렌티스 홀, ISBN 0-13-495656-7

[10] Adachi, Sadao (1993-01-01). Properties of Aluminium Gallium Arsenide. ISBN 9780852965580.

[Debbar-11] Debbar, N.; Biswas, Dipankar; Bhattacharya, Pallab (1989). "Conduction-band offsets in pseudomorphic InxGa1-xAs/Al0.2Ga0.8As quantum wells (0.07≤x≤0.18) measured by deep-level transient spectroscopy". Physical Review B. 40 (2): 1058–1063. Bibcode:1989PhRvB..40.1058D. doi:10.1103/PhysRevB.40.1058. PMID 9991928.

[12] Conley, J.; Duke, C.; Mahan, G.; Tiemann, J. (1966). "Electron Tunneling in Metal–Semiconductor Barriers". Physical Review. 150 (2): 466. Bibcode:1966PhRv..150..466C. doi:10.1103/PhysRev.150.466.

[13] Bendaniel, D.; Duke, C. (1966). "Space-Charge Effects on Electron Tunneling". Physical Review. 152 (2): 683. Bibcode:1966PhRv..152..683B. doi:10.1103/PhysRev.152.683.

[14] 그리피스, 데이비드 J. (2004)양자역학 입문 (제2판)프렌티스 홀.ISBN 0-13-11892-7

[15] Ivanov, Sergei A.; Piryatinski, Andrei; Nanda, Jagjit; Tretiak, Sergei; Zavadil, Kevin R.; Wallace, William O.; Werder, Don; Klimov, Victor I. (2007). "Type-II Core/Shell CdS/ZnSe Nanocrystals: Synthesis, Electronic Structures, and Spectroscopic Properties". Journal of the American Chemical Society. 129 (38): 11708–19. doi:10.1021/ja068351m. PMID 17727285.

[Robel-16] Robel, István; Kuno, Masaru; Kamat, Prashant V. (2007). "Size-Dependent Electron Injection from Excited CdSe Quantum Dots into TiO2Nanoparticles". Journal of the American Chemical Society. 129 (14): 4136–7. doi:10.1021/ja070099a. PMID 17373799.

[1]

[2]

[3]

[4]

[5]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[15]

[16]

Search

헤테로 접합

네임스페이스

더

목차

제조 및 응용 프로그램

에너지 밴드 얼라인먼트

유효 질량 불일치

나노스케일 헤테로 접합

「」를 참조해 주세요.

레퍼런스

추가 정보

Search

헤테로 접합

제조 및 응용 프로그램

에너지 밴드 얼라인먼트

유효 질량 불일치

나노스케일 헤테로 접합

「 」를 참조해 주세요.

레퍼런스

추가 정보

「」를 참조해 주세요.