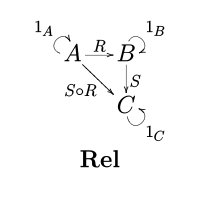
관계 카테고리

수학에서 범주 Rel은 집합의 클래스를 개체로, 이진 관계는 형태소로 가집니다.

형태론(또는 화살표) R : 이 범주에서 A → B는 집합 A와 B 사이의 관계이므로 R a A × B이다.

두 관계 R: A → B 및 S: B → C의 구성은 다음과 같이 주어진다.

(a, c) B, (a, b) R 및 (b, c) ^[1]S에 대하여 S o R for

Rel은 "집합 대응 범주"^[2]라고도 불립니다.

특성.

범주 Rel에는 (넓은) 하위 범주로 설정된 집합의 범주가 있습니다. 여기서 집합의 화살표 f : X → Y는 (x, y) f F f f(x) = ^[3][4]y로 정의된 F x X × Y 관계에 해당합니다.

Rel의 모르피즘은 관계이며, Rel과 반대 범주의 대응하는 모르피즘은 화살표가 반전되므로 역관계이다.따라서 Rel은 그 반대이며 자기 이중적입니다.^[5]

역관계로 표현되는 혁명은 Rel을 단검 카테고리로 만들기 위한 단검을 제공합니다.

범주는 호름 함수에 의해 주어진 두 개의 함수자를 가진다. 즉, 이진 관계 R a A × B와 그 전치^T R b B × A는 R^T R 또는 R R로^T 구성될 수 있다.첫 번째 구성은 A에 균질한 관계를 가져오고 두 번째 구성은 B에 있습니다.이러한 홈 펑터의 이미지는 Rel 자체이므로 이 경우 홈은 내부 홈 펑터입니다.내부 홈 펑터를 갖춘 Rel은 닫힌 카테고리이며 단검 컴팩트 카테고리입니다.

범주 Rel은 함수자가 멱집합에 해당하는 모나드의 Kleisli 범주로 설정된 범주에서 얻을 수 있으며, 이는 공변 함수자로 해석됩니다.

Rel의 곱은 (세트와 같은 데카르트 곱이 아니라) 분리된^{[5]: 181} 결합에 의해 제공되며, 공동 생산물도 제공된다는 사실이 언뜻 보기에 조금 놀랍다.

Rel은 단상 폐쇄형이며, 단상 생성물 A a B와 내부 홈 A b B는 모두 집합의 데카르트 곱에 의해 주어진다.

범주 Rel은 피터 J.의 우화라고 불리는 대수 구조의 원형이었다. 1990년 프레이드와 안드레 세드로프.^[6]정규 범주 및 펑터 F: A → B로 시작하여 유도 펑터 Rel(A,B) → Rel(FA, FB)의 특성을 기록합니다.예를 들어 구성, 변환 및 교차점을 보존합니다.그런 특성들은 우화에 대한 공리를 제공하기 위해 사용된다.

오브젝트로서의 관계

David Rydehored와 Rod Burstall은 Rel이 동질적인 관계를 갖는 객체를 가지고 있다고 간주합니다.예를 들어 A는 집합이고 R ⊆ A × A는 A 위의 2진 관계이다.이 범주의 모피즘은 관계를 유지하는 집합 간의 함수입니다.예를 들어, S ⊆ B × B는 제2의 관계이며, f: A → B는 ${\displaystyle x}$ ${\displaystyle R}$ ${\displaystyle ⟹f}$ (${\displaystyle x}$ ) ${\displaystyle S}$f (${\displaystyle y}$)$$, { $displaystyle xRy\implies$ f$(x) Sf($^[7]y$)},$ f는 형태소이다.

Adamek, Herrlich 및 Strecker에 의해 동일한 아이디어가 제시되어 객체(A, R) 및 (B, S)를 지정하고 집합과 관계를 ^[8]지정한다.

레퍼런스

• Francis Borceux (1994). Handbook of Categorical Algebra: Volume 2, Categories and Structures. Cambridge University Press. p. 115. ISBN 978-0-521-44179-7.