
바람에 날리는 기의 표면은 변형 다지관의 예다. 이동 표면의 미적분(CMS)은 다지관을 변형시키기 위한 고전적인 텐서 미적분의 확장이다. CMS의 중심에는 Jacques Hadamard에 의해 원래 정의가 제시된 Tensorial Time Derival 이(가) 있다. 텐서(tensor)에 적용했을 때 텐서tensor)를 생성한다는 점에서 차동 다지관의
Tensorial Time Derival 이(가) 있다. 텐서(tensor)에 적용했을 때 텐서tensor)를 생성한다는 점에서 차동 다지관의 공변량 파생상품 {\과 유사한 역할을 한다.
공변량 파생상품 {\과 유사한 역할을 한다.

자크 살로몬 하다마르, 1865–1963 CE 프랑스 수학자 이(가) 시간 유사 t 에 의해 색인화된 표면 의 진화라고
색인화된 표면 의 진화라고 가정합시다
가정합시다 표면 속도 및
표면 속도 및 연산자 {\의 정의는 CMS의 기하학적 기초가 된다
연산자 {\의 정의는 CMS의 기하학적 기초가 된다 . 속도 C는 표면 의
. 속도 C는 표면 의 순간 정상 방향의 변형률이다. 점 에서
순간 정상 방향의 변형률이다. 점 에서 의 값은 한계로 정의됨
의 값은 한계로 정의됨

여기서 는 P 지점에서
P 지점에서 에 수직인 직선에 있는 the
에 수직인 직선에 있는 the t 의 포인트다. 이 정의는 아래의 첫 번째 기하학적 도형에 설명되어 있다. 속도 은
t 의 포인트다. 이 정의는 아래의 첫 번째 기하학적 도형에 설명되어 있다. 속도 은 서명된 수량: ∗이(가) 선택한 정상 방향으로 가리킬
서명된 수량: ∗이(가) 선택한 정상 방향으로 가리킬 때 양이고, 그렇지 않을 경우 음이다. 와
때 양이고, 그렇지 않을 경우 음이다. 와 의 관계는 기초 미적분학에서 위치와 속도 사이의 관계와 유사하다
의 관계는 기초 미적분학에서 위치와 속도 사이의 관계와 유사하다 . 두 가지 양을 알면 분화 또는 통합으로 다른 것을 구성할 수 있다.
. 두 가지 양을 알면 분화 또는 통합으로 다른 것을 구성할 수 있다.

불변 필드 F의 / t -변환성의 기하학적 구조
기하학적 구조 에 정의된 스칼라 필드 F에 대한 Tensorial Time 파생상품 은
Tensorial Time 파생상품 은 (는) 순간적으로
(는) 순간적으로 방향으로 F {\의 변화율이다.
방향으로 F {\의 변화율이다.

이 정의는 두 번째 기하학적 그림에도 설명되어 있다.
위의 정의들은 기하학적이다. 해석적 설정에서는 이러한 정의를 직접 적용할 수 없을 수 있다. CMS는 미적분학 및 미분 기하학으로부터의 기초적 연산의 관점에서 C와 에 대한 해석적 정의를 제공한다.
C와 에 대한 해석적 정의를 제공한다.
분석적 정의
및 의 분석적 정의에 대해서는 다음이 하는
의 분석적 정의에 대해서는 다음이 하는 S 의 진화를 고려하십시오
S 의 진화를 고려하십시오

여기서 Z는 일반 곡선 공간 좌표, S은
일반 곡선 공간 좌표, S은 표면 좌표다. 관례에 따라 함수 인수의 텐서 인덱스는 삭제된다. 따라서 위의 방정식은 이 아니라
표면 좌표다. 관례에 따라 함수 인수의 텐서 인덱스는 삭제된다. 따라서 위의 방정식은 이 아니라 을(를) 포함한다
을(를) 포함한다 속도 객체 = i {}}은 부분파생물로 정의된다
속도 객체 = i {}}은 부분파생물로 정의된다 .
.

속도 은 공식으로 가장 직접적으로 계산할 수 있다 .
.

여기서 는 정규 벡터 → {\vec의 공변량 성분이다

Also, defining the shift tensor representation of the Surface's Tangent Space  and the Tangent Velocity as
and the Tangent Velocity as  , then the definition of the 변수
, then the definition of the 변수 F 읽기용 파생 모델
F 읽기용 파생 모델

여기서 은 S의 공변량 파생물이다.
S의 공변량 파생물이다.
텐셔너의 경우 적절한 일반화가 필요하다. 대표적인 텐서 에 대한 적절한 정의
대한 적절한 정의

where  are Christoffel symbols and
are Christoffel symbols and  is the surface's appropriate temporal symbols (은 표면의 곡률 모양 연산자를 행렬로 표현한 것이다
is the surface's appropriate temporal symbols (은 표면의 곡률 모양 연산자를 행렬로 표현한 것이다 .)
.)
-파생물의 속성
속성
}} -분열은 수축과 함께 통하며, 모든 지수 수집에 대한 제품 규칙을 만족한다.
수축과 함께 통하며, 모든 지수 수집에 대한 제품 규칙을 만족한다.

공간 텐셔너의 표면 제한에 대한 체인 규칙을 준수한다.

체인 규칙은 공간 "메트릭스"의 device가 사라지는 것을 보여준다.
사라지는 것을 보여준다.

where  and
and  are covariant and contravariant metric tensors,
are covariant and contravariant metric tensors,  is the Kronecker delta symbol, and
is the Kronecker delta symbol, and  and
and  are the Levi-Civita 기호. Levi-Civita 기호에 관한 주요 기사는 그들을 데카르트 좌표계에 대해 설명한다. 앞의 규칙은 일반 좌표에서 유효하며, 여기서 Levi-Civita 기호의 정의는 공변량 미터법 텐서 의 결정요인의 제곱근을 포함해야 한다
are the Levi-Civita 기호. Levi-Civita 기호에 관한 주요 기사는 그들을 데카르트 좌표계에 대해 설명한다. 앞의 규칙은 일반 좌표에서 유효하며, 여기서 Levi-Civita 기호의 정의는 공변량 미터법 텐서 의 결정요인의 제곱근을 포함해야 한다
}} -분해성 표
표
surface 주요 표면 객체의 파생 모델은 매우 간결하고 매력적인 공식으로 이어진다. 공변량 지표면 텐서 및
매우 간결하고 매력적인 공식으로 이어진다. 공변량 지표면 텐서 및 반대방향 지표면 텐서 에 적용하면 다음과 같은 ID가 나타난다
반대방향 지표면 텐서 에 적용하면 다음과 같은 ID가 나타난다
![{\displaystyle {\begin{aligned}{\dot {\nabla }}S_{\alpha \beta }&=0\\[8pt]{\dot {\nabla }}S^{\alpha \beta }&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a5f6e7f6ec7eae3edd762cb8941e78157ec50ef)
여기서 과 (와) 은
(와) 은 공변량 2배이고 곡률도 2배이다. 이러한 곡률 텐서뿐만 텐서 B β α {\ B_ }^{\도 충족한다
공변량 2배이고 곡률도 2배이다. 이러한 곡률 텐서뿐만 텐서 B β α {\ B_ }^{\도 충족한다
![{\displaystyle {\begin{aligned}{\dot {\nabla }}B_{\alpha \beta }&=\nabla _{\alpha }\nabla _{\beta }C+CB_{\alpha \gamma }B_{\beta }^{\gamma }\\[8pt]{\dot {\nabla }}B_{\beta }^{\alpha }&=\nabla _{\beta }\nabla ^{\alpha }C+CB_{\gamma }^{\alpha }B_{\beta }^{\gamma }\\[8pt]{\dot {\nabla }}B^{\alpha \beta }&=\nabla ^{\alpha }\nabla ^{\beta }C+CB^{\gamma \alpha }B_{\gamma }^{\beta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f2e2b5072dab70f45f0a4d67650ce163479475c)
시프트 텐서 i 과 (와) 정상 N이
(와) 정상 N이 (가) 충족됨
(가) 충족됨
![{\displaystyle {\begin{aligned}{\dot {\nabla }}Z_{\alpha }^{i}&=N^{i}\nabla _{\alpha }C\\[8pt]{\dot {\nabla }}N^{i}&=-Z_{\alpha }^{i}\nabla ^{\alpha }C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04583f21c0d1c60912dadb938116e2c2c65a548d)
마지막으로 표면 Levi-Civita 기호 β {\  β \이 충족된다
β \이 충족된다 .
.
![{\displaystyle {\begin{aligned}{\dot {\nabla }}\varepsilon _{\alpha \beta }&=0\\[8pt]{\dot {\nabla }}\varepsilon ^{\alpha \beta }&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dace09f2d05c3613013ee0373e46cfbbfe808fa)
통합의 시간 차별화
CMS는 볼륨과 표면 통합의 시간 분화를 위한 규칙을 제공한다.
참조










 P 지점에서
P 지점에서

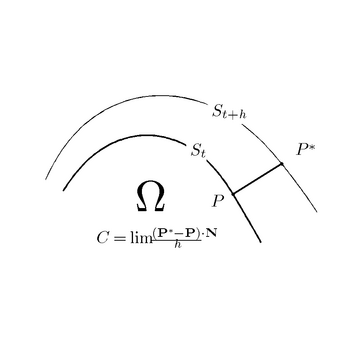




 S
S 
 일반
일반  표면 좌표다. 관례에 따라 함수 인수의 텐서 인덱스는 삭제된다. 따라서 위의 방정식은
표면 좌표다. 관례에 따라 함수 인수의 텐서 인덱스는 삭제된다. 따라서 위의 방정식은 







 대한 적절한 정의
대한 적절한 정의 













![{\displaystyle {\begin{aligned}{\dot {\nabla }}S_{\alpha \beta }&=0\\[8pt]{\dot {\nabla }}S^{\alpha \beta }&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a5f6e7f6ec7eae3edd762cb8941e78157ec50ef)
 (와)
(와)  공변량
공변량 ![{\displaystyle {\begin{aligned}{\dot {\nabla }}B_{\alpha \beta }&=\nabla _{\alpha }\nabla _{\beta }C+CB_{\alpha \gamma }B_{\beta }^{\gamma }\\[8pt]{\dot {\nabla }}B_{\beta }^{\alpha }&=\nabla _{\beta }\nabla ^{\alpha }C+CB_{\gamma }^{\alpha }B_{\beta }^{\gamma }\\[8pt]{\dot {\nabla }}B^{\alpha \beta }&=\nabla ^{\alpha }\nabla ^{\beta }C+CB^{\gamma \alpha }B_{\gamma }^{\beta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f2e2b5072dab70f45f0a4d67650ce163479475c)
 (와) 정상
(와) 정상  (가) 충족됨
(가) 충족됨 ![{\displaystyle {\begin{aligned}{\dot {\nabla }}Z_{\alpha }^{i}&=N^{i}\nabla _{\alpha }C\\[8pt]{\dot {\nabla }}N^{i}&=-Z_{\alpha }^{i}\nabla ^{\alpha }C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04583f21c0d1c60912dadb938116e2c2c65a548d)


![{\displaystyle {\begin{aligned}{\dot {\nabla }}\varepsilon _{\alpha \beta }&=0\\[8pt]{\dot {\nabla }}\varepsilon ^{\alpha \beta }&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dace09f2d05c3613013ee0373e46cfbbfe808fa)


