판의 진동 은 기계적 진동 에 관한 보다 일반적인 문제의 특별한 경우입니다.판의 움직임을 지배하는 방정식은 판의 한 치수가 다른 두 치수보다 훨씬 작기 때문에 일반적인 3차원 물체에 비해 간단하다. 이것은 2차원 판 이론 이 판과 같은 물체의 실제 3차원 움직임에 대해 훌륭한 근사치를 제공할 것이라는 것을 시사하며,[1]
판의 움직임을 설명하기 위해 개발된 몇 가지 이론이 있다. 가장 일반적으로 사용되는 것은 키르히호프-러브 [2] [3] [4] 후자의 이론은 엘리샤코프 에 [5] 이 이론들에 의해 예측된 지배 방정식에 대한 해법은 우리에게 자유 조건과 강제 조건 모두에서 판 과 같은 물체의 행동에 대한 통찰력을 줄 수 있다. 여기에는 파동의 전파와 평판의 정파 및 진동 모드에 대한 연구가 포함됩니다. 판의 진동에 대한 주제는 레이사,[6] [7] [8] [9] [10] [11] [12] [13] [14]
키르히호프 러브 플레이트 키르히호프-러브 플레이트의 역학에 대한 지배 방정식은 다음과 같습니다.
N α β , β = J 1 u ¨ α M α β , α β + q ( x , t ) = J 1 w ¨ − J 3 w ¨ , α α 디스플레이 스타일 N_{\alpha \lapa },\lapa }~{\ddot {u}}_{\M_{\alpha \lapa }+q(x,t)&= J_{1}~{\dot {w}}-J_{3}~{\ddot {w}}_{,\alpha \alpha }\end{aligned}}} 여기 uα {\ displaystyle u_{\alpha } w displaystyle } displaystyle 3 가리키는 뜨거운 힘과 순간은 다음과 같이 정의된다.
N α β := ∫ − h h σ α β d x 3 그리고. M α β := ∫ − h h x 3 σ α β d x 3 . {\displaystyle N_{\alpha \displaystyle }:=\int _{-h}^{h}^{h}\display M_{text_{3}\display M_{\alpha\display}=\int _{-h}^{h}x}~{\displaystyp}_{\display}. } 플레이트의 두께는 2시간 (\displaystyle 2h) β sigma {\alpha \beta } 지배 방정식의 도함수는 다음과 같이 정의된다.
u ˙ i := ∂ u i ∂ t ; u ¨ i := ∂ 2 u i ∂ t 2 ; u i , α := ∂ u i ∂ x α ; u i , α β := ∂ 2 u i ∂ x α ∂ x β {\displaystyle\dot {u}_{i}: =paramfrac({param u_{i}}{\param t}}~;~{\ddot {u}}_{i}): = specfrac {\spec ^{2}u_{i}~;~u_{i,\alpha}:= specfrac {\spec u_{i}}~;~u_{i,\alpha }{i}~;~u_pec frac {\spec t^{2}u_{{i}_{i}}{i}{i}{i}} {\alpha } 여기서 라틴 지수는 1에서 3으로, 그리스 지수는 1에서 2로 이동합니다. 반복된 지수에 대한 합계가 암시된다. x ({ displaystyle x_{3}) 반면 ({displaystyle x_1 및 x displaystyle x_{ 두께 2시간 (\displaystyle 2h) δ\displaystyle \rho
J 1 := ∫ − h h ρ d x 3 = 2 ρ h 그리고. J 3 := ∫ − h h x 3 2 ρ d x 3 = 2 3 ρ h 3 . {\displaystyle J_{1}:=\int _{-h}^{h}\rho ~2\rho h\text {and}}\rho J_{3}:=\int _{-h}^{h}x_{2}~\rho ~\rho_{3}^{ho}, {3}. } 등방성 키르히호프-러브 플레이트 등방성 및 균질판의 경우 응력-변형 관계는 다음과 같다.
[ σ 11 σ 22 σ 12 ] = E 1 − ν 2 [ 1 ν 0 ν 1 0 0 0 1 − ν ] [ ε 11 ε 22 ε 12 ] . {\displaystyle {bmatrix} \\displaystyle _{11} \\display _ {12} \end {bmatrix} = displayac {E} {1-\nu ^{2}} {\displaystyle {bmatrix} 1 & 0\nu & 1&0&0&1-nu\nu {b} } 여기서 α displaystyle \varepsilon {\alpha \beta displaystyle \nu} 비율 입니다. Kirchhoff-Love 플레이트의 변형-변위 관계는 다음과 같습니다.
ε α β = 1 2 ( u α , β + u β , α ) − x 3 w , α β . {\displaystyle \varepsilon _{\alpha \alpha } = specfrac {1}{2} ( u _ { \ alpha } + u _ { \ alpha } 、 w _ { , \ alpha } 、 } 따라서 이러한 응력에 대응하는 모멘트는 다음과 같습니다.
[ M 11 M 22 M 12 ] = − 2 h 3 E 3 ( 1 − ν 2 ) [ 1 ν 0 ν 1 0 0 0 1 − ν ] [ w , 11 w , 22 w , 12 ] {\displaystyle {bmatrix} M_{11}\M_{22}\M_{12}\end{bmatrix}=-{\cfrac {2h^3}E}{3(1-\nu ^{2}}}}}~{\cfrac {bmatrix}1&0\nu} 평면 내 변위 u α displaystyle u_{\alpha \beta
D ∇ 2 ∇ 2 w = q ( x , t ) − 2 ρ h w ¨ {\displaystyle D\nabla ^{2}w=q(x,t)-2\rho havdot {w}}, 여기 (\displaystyle ) 두께 2시간 (\ 2h D := 2 h 3 E 3 ( 1 − ν 2 ) . {\displaystyle D:=cfrac {2h^{3}E}{3(1-\nu ^{2}}}}, 위의 방정식은 대체 표기법으로도 쓸 수 있습니다.
μ Δ Δ w − q ^ + ρ w t t = 0 . \displaystyle \mu \Delta w-{\hat {q}}+\rho w_{tt}=0,} 고체역학 에서 판은 종종 2차원 탄성체로 모델링되는데, 그 전위 에너지는 판이 늘어나는 방식보다는 평면 구성에서 어떻게 구부러지는지에 따라 달라집니다(드럼헤드 같은 막의 경우).이 때 진동판 은 진동 드럼과 같은 형태로 모델화할 수 있다. 그러나 평형위치에서 판의 수직변위 w에 대한 편미분방정식 은 2차식이 아니라 w 의 라플라시안 제곱을 포함한 4차식이므로 그 질적 거동은 원형막 드럼과 근본적으로 다르다.
등방성 판의 자유 진동 자유진동의 경우 외력q 는 0이며 등방성 플레이트의 지배방정식은 다음과 같이 감소한다.
D ∇ 2 ∇ 2 w = − 2 ρ h w ¨ {\displaystyle D\nabla ^{2}\displayla ^{2}w=-2\rho h2dot {w}} 또는
μ Δ Δ w + ρ w t t = 0 . \displaystyle \mu \Delta w+\rho w_{tt}=0,} 이 관계는 플레이트의 [15] 플레이트의 전위 에너지 밀도는 플레이트의 변형 방법과 플레이트의 평균 곡률 및 가우스 곡률에 따라 달라집니다. 작은 변형의 경우, 평균 곡률은 운동 평형으로부터의 판의 수직 변위인 w 로 표현되며, δw, w 의 라플라시안, 가우스 곡률은 Monge-Amper 연산자xx yy 2 xy 따라서 플레이트 δ의 총 위치에너지는 다음과 같은 형태를 가진다.
U = ∫ Ω [ ( Δ w ) 2 + ( 1 − μ ) ( w x x w y y − w x y 2 ) ] d x d y {\displaystyle U=\int _{\Omega }[((Delta w)^2}+(1-\mu)(w_{x}w_{y}-w_{xy}^2}) >,display,dy} 전체적인 필수적이지 않은 정규화 상수를 제외하고요. 여기서 μ는 재료의 특성에 따른 상수이다.
운동 에너지는 형태의 적분에 의해 주어진다.
T = ρ 2 ∫ Ω w t 2 d x d y . {\displaystyle T=black {rho }{2}\int _{\Omega }w_{t}^{2},dy. } 해밀턴의 원리 는 w가 총 에너지 T+U 의 변화 에 관한 정지점이라고 주장 한다.결과적으로 생기는 편미분 방정식은
ρ w t t + μ Δ Δ w = 0. \displaystyle w_{tt}+\mu \Delta w=0., 원형 플레이트 자유롭게 진동하는 원형 플레이트의 경우 = w r t displaystyle =w(r,t
∇ 2 w ≡ 1 r ∂ ∂ r ( r ∂ w ∂ r ) . \displaystyle \frac {1} {r} {\frac r} {\frac r} \ left ( r frac w } {\fright ) 。 } 따라서 2시간 (\displaystyle 2h)
1 r ∂ ∂ r [ r ∂ ∂ r { 1 r ∂ ∂ r ( r ∂ w ∂ r ) } ] = − 2 ρ h D ∂ 2 w ∂ t 2 . {\displaystyle {\frac {1}{r}{\frac r}\left[rfrac {\frac {1}{\frac r}{\frac r}{\frac w}{\frac r}\left(rfrac w}{\frac w}{\fright}\frac r}\frac =\fright } 확장,
∂ 4 w ∂ r 4 + 2 r ∂ 3 w ∂ r 3 − 1 r 2 ∂ 2 w ∂ r 2 + 1 r 3 ∂ w ∂ r = − 2 ρ h D ∂ 2 w ∂ t 2 . \displaystyle {\frac r^{4}{\frac r^{4}+{\frac {2}{r}{\frac r^{3}w}-{\frac {1}{r^{2}}{\frac {\frac {\frac ^2}{\frac {\frac } {\frac {\frac} } 이 방정식을 풀기 위해 우리는 변수 분리 개념을 사용하고 형태의 해법을 가정한다.
w ( r , t ) = W ( r ) F ( t ) . \displaystyle w(r,t)=W(r)F(t), } 이 가정된 솔루션을 지배 방정식에 연결하면
1 β W [ d 4 W d r 4 + 2 r d 3 W d r 3 − 1 r 2 d 2 W d r 2 + 1 r 3 d W d r ] = − 1 F d 2 F d t 2 = ω 2 (\displaystyle {1}{\beta W}}\left[{\frac {d^{4}) }W}{dr^{4}}+{\frac {2}{r}}{\frac {d^{3} }W}{dr^{3}}-{\frac {1}{r^{2}}{\frac {d^{2}W}{dr^{2}}+{\frac {1}{r^{3}}{\frac {dr}}\right}=-{\frac}{frac {F}{f}}}{frac}{frac}}{frac {fr}}}{frac}}}}}}}{frac}}}}{{fr}}}}}}}}}{{{fr}}}}}}}}} }F}{dt^{2}}=\obega^{2}} 여기서 θ (\ displaystyle \obega 2}) 상수 = 2 µ D (\display \display 2\rho .
F ( t ) = 레 [ A e i ω t + B e − i ω t ] . {\displaystyle F(t)=context{Re}}[Ae^{i\omega t}+Be^{-i\omega t}], } 왼쪽 방정식은 다음과 같이 쓸 수 있습니다.
d 4 W d r 4 + 2 r d 3 W d r 3 − 1 r 2 d 2 W d r 2 + 1 r 3 d W d r = λ 4 W {\displaystyle\frac{d^{4} }W}{dr^{4}}+{\frac {2}{r}}{\frac {d^{3} }W}{dr^{3}}-{\frac {1}{r^{2}}{\frac {d^{2}W}{dr^{2}}+{\frac {1}{r^3}}{\frac {dr}}=\lambda ^{4} W} 여기서 λ = β ω displaystyle displayda display obega 플레이트에 적합한 이 고유값 문제에 대한 일반적인 해법은 다음과 같은 형태를 가진다.
W ( r ) = C 1 J 0 ( λ r ) + C 2 I 0 ( λ r ) {\displaystyle W(r)=C_{1}J_{0}(\lambda r)+C_{2} I_{0}(\lambda r)} 여기 ({ displaystyle J_{0}) 0차 베셀 함수 I displaystyle I_{0}) 0차 변형 베셀 함수입니다.상수 ({ displaystyle C_{ 및 C displaystyle C_{ 둘레가 고정된 반지름 displaystyle )
W ( r ) = 0 그리고. d W d r = 0 에 r = a . \displaystyle W(r)=0\quad\text{dW}{dr}=0\quadr=a, } 이러한 경계 조건으로부터 우리는 다음을 알 수 있습니다.
J 0 ( λ a ) I 1 ( λ a ) + I 0 ( λ a ) J 1 ( λ a ) = 0 . {\displaystyle J_{0}(\lambda a) I_{1}(\lambda a)+ I_{0}(\lambda a) J_{1}(\lambda a)=0,} 이 방정식은 δn displaystyle \displayda {n}( δn = β displaystyle \displayda {n displayda ^{ displayrt }}}} }
w ( r , t ) = ∑ n = 1 ∞ C n [ J 0 ( λ n r ) − J 0 ( λ n a ) I 0 ( λ n a ) I 0 ( λ n r ) ] [ A n e i ω n t + B n e − i ω n t ] . {\displaystyle w(r,t)=\sum _{n=1}^{\infty}C_{n}\left[ J_{0}(\lambda_{n}r)-{\frac {J_{0}(\lambda_{n}a)}{ I_{0}(\lambda_{n}a)}} I_{0}(\lambda_{n}r)\right][ A_{n}e^{i\omega_{n}t}+B_{n}e^{-i\omega_{n}t}], } 소정의 주파수 displaystyle\obega_{ 푸리에 = 초기조건 계수 A n displaystyle A_{n}, n displaystyle B_{n} displaystyle C_{n} 값
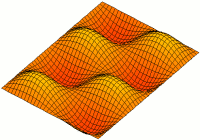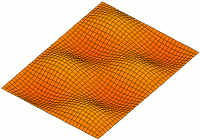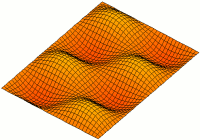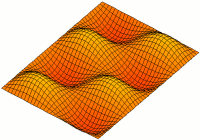
직사각형 플레이트 ( x x x x_{1}, x_{2}) 치수 a displaystyle \times ) x displaystyle x_{3 두께 displaystyle ) 플레이트의 자유 진동 모드를 찾습니다.
형상의 변위 필드를 가정합니다.
w ( x 1 , x 2 , t ) = W ( x 1 , x 2 ) F ( t ) . {\displaystyle w(x_{1},x_{2},t)= W(x_{1},x_{2}) F(t), .} 그리고나서,
∇ 2 ∇ 2 w = w , 1111 + 2 w , 1212 + w , 2222 = [ ∂ 4 W ∂ x 1 4 + 2 ∂ 4 W ∂ x 1 2 ∂ x 2 2 + ∂ 4 W ∂ x 2 4 ] F ( t ) \displaystyle \displayla ^{2}\displayla ^{2}w_{,111}+2w_{,1212}+w_{,2222}=\left[\frac {\displaystyle ^{4} W}{\partial x_{1}^{4}}+2{\frac {\partial ^{4} W}{\partial x_{1}^{2}\partial x_{2}^{\frac {\partial ^{4}+ W}{\partial x_{2}^{4}}\right]F(t)} 그리고.
w ¨ = W ( x 1 , x 2 ) d 2 F d t 2 . {\displaystyle {w}}=W(x_{1},x_{2}){\frac {d^{2} }F}{dt^{2}}, } 이것들을 지배 방정식에 대입하면
D 2 ρ h W [ ∂ 4 W ∂ x 1 4 + 2 ∂ 4 W ∂ x 1 2 ∂ x 2 2 + ∂ 4 W ∂ x 2 4 ] = − 1 F d 2 F d t 2 = ω 2 {\displaystyle {D}{2\rho hW}}\left[{\frac {\partial ^{4} W}{\partial x_{1}^{4}}+2{\frac {\partial ^{4} W}{\partial x_{1}^{2}\partial x_{2}^{\frac {\partial ^{4}+ W}{\partial x_{2}^{4}}\right]=-{\frac {1}{F}}{\frac {d^{2} }F}{dt^{2}}=\obega^{2}} 여기 (\ displaystyle \obega 2}) (\displaystyle ) , 오른쪽 x1 , x2 displaystyle x_1}, x_{2
F ( t ) = A e i ω t + B e − i ω t . {\displaystyle F(t)= Ae^{i\omega t}+Be^{-i\omega t}, } 왼쪽부터.
∂ 4 W ∂ x 1 4 + 2 ∂ 4 W ∂ x 1 2 ∂ x 2 2 + ∂ 4 W ∂ x 2 4 = 2 ρ h ω 2 D W =: λ 4 W 디스플레이 스타일 W}{\partial x_{1}^{4}}+2{\frac {\partial ^{4} W}{\partial x_{1}^{2}\partial x_{2}^{\frac {\partial ^{4}+ W}{\partial x_{2}^{4}}=blac {2\rho h\omega ^{2}}{D}}W=:\lambda ^{4} W} 어디에
λ 2 = ω 2 ρ h D . {\displaystyle \displayda ^{2}=\Omega {frac {2\rho h}{D}}, } 위의 방정식이 바이하모닉 고유값 문제이기 때문에, 우리는 형태의 푸리에 확장 해법을 찾는다.
W m n ( x 1 , x 2 ) = 죄 m π x 1 a 죄 n π x 2 b . {\displaystyle W_{mn}(x_{1},x_{2})=\sin {frac {m\pi x_{1}{a}}\sin {frac {n\pi x_{2}}{b}}, } 이 솔루션이 단순히 지지된 가장자리로 자유롭게 진동하는 직사각형 플레이트의 경계 조건을 충족하는지 확인할 수 있습니다.
w ( x 1 , x 2 , t ) = 0 에 x 1 = 0 , a 그리고. x 2 = 0 , b M 11 = D ( ∂ 2 w ∂ x 1 2 + ν ∂ 2 w ∂ x 2 2 ) = 0 에 x 1 = 0 , a M 22 = D ( ∂ 2 w ∂ x 2 2 + ν ∂ 2 w ∂ x 1 2 ) = 0 에 x 2 = 0 , b . {\displaystyle {arged}w(x_{1},x_{2},t)=0&\display {at}\display x_{1}=0,a\display x_{2}=0,b\ M_{11}=D\left({\frac {{2}w}{\frac x_{1}^{2}w}+\frac {\frac x_{2}^{2}}\right)=0&\frac {\text}\frac x_{1}=0,a\frac M_{22}=D\left({\frac {{2}w}{\frac x_{2}^{2}w}+\frac {\frac x_{1}{2}}\right)=0&\frac {\text{at}\frac x_{2}=0,b. \end { aligned}} 용액을 바이하모닉 방정식에 연결하면
λ 2 = π 2 ( m 2 a 2 + n 2 b 2 ) . {\displaystyle \pi da ^{2}=\pi ^{2}\frac {m^{2}}{a^{2}}+{\frac {n^{2}}{b^{2}}\right}, } § 2 displaystyle \lambda 2})
ω m n = ( m 2 a 2 + n 2 b 2 ) D π 4 2 ρ h . {\displaystyle \mega _{mn}=\leftfrac {m^{2}}+{\frac {n^{2}}{b^{2}}\right}{\fracrt {D\pi ^{4}}{2\rho}}}, } 따라서 플레이트 방정식의 일반적인 해는
w ( x 1 , x 2 , t ) = ∑ m = 1 ∞ ∑ n = 1 ∞ 죄 m π x 1 a 죄 n π x 2 b ( A m n e i ω m n t + B m n e − i ω m n t ) . ({displaystyle w(x_{1},x_{2},t)=\sum _{m=1}^{\infty}\sin {frac {m\pi x_{1}{a}}\sin {frac {n\pi x_{2}}{b}\lefty(A_mne})_mni}_{mni}_mn}_mnfty}_mn}\sin {mn} } A n displaystyle A_{ B n ({ displaystyle B_{mn}) 값 예를 들어,
w ( x 1 , x 2 , 0 ) = φ ( x 1 , x 2 ) 에 x 1 ∈ [ 0 , a ] 그리고. ∂ w ∂ t ( x 1 , x 2 , 0 ) = ψ ( x 1 , x 2 ) 에 x 2 ∈ [ 0 , b ] {\displaystyle w(x_{1},x_{2})=\varphi(x_{1},x_{2}\in [0,a]\displays {text{and}\displays {frac {\displays w}{\displayst})={x_{1}, {x}, {x}, 우리는,
A m n = 4 a b ∫ 0 a ∫ 0 b φ ( x 1 , x 2 ) 죄 m π x 1 a 죄 n π x 2 b d x 1 d x 2 B m n = 4 a b ω m n ∫ 0 a ∫ 0 b ψ ( x 1 , x 2 ) 죄 m π x 1 a 죄 n π x 2 b d x 1 d x 2 . 디스플레이 스타일 A_{mn}&=snfrac {4}{ab}\int _{0}^{a}\int _{0}^{b}\varphi (x_{1}x_{2})\sin {frac {m\pi x_{1}{a}\sin {n\pi x_{2}}\sin {b}\d}\d}\dx} \end { aligned}} 레퍼런스 ^ Reddy, J. N., 2007 , 탄성판 및 쉘 이론 및 분석 , CRC Press, Taylor 및 Francis. ^ A . E. H. Love , 탄성 껍데기의 작은 자유 진동과 변형 에 대한 철학적인 전달.로얄 소사이어티(런던), 1888년, Vol. série A, N° 17 p. 491–549. ^ Uflyand, Ya., S., 1948, 빔과 플레이트의 횡진동에 의한 파동 전파, PMM: 응용 수학 및 역학 저널, 제12권, 페이지 287-300(러시아어) ^ Mindlin, R.D. 1951, 등방성 탄성판의 휨 운동에 대한 회전 관성 및 전단 영향, ASME Journal of Applied Mechanics, Vol. 18 페이지 31–38 ^ Elishakoff , I., 2020, Timoshenko-Ehrenfest 빔 과 Uflyand-Mindlin 플레이트 이론 에 관한 핸드북 , 세계과학, 싱가포르,ISBN 978-981-3236-51-6 ^ 레이사, A.W., 1969, 플레이트의 진동, NASA SP-160, 워싱턴 D.C.: 미국 정부 인쇄소 ^ 레이사, A.W. 및 Qatu, M.S., 2011, 뉴욕, Vibration of Continuous Systems, Mc Graw-Hill ^ Gontkevich, V. S., 1964, 키예프, "Natural Vibrations of Plate and Shells, Naukova Dumka" 출판사, 1964(러시아어); (영어 번역: 록히드 미사일 우주 회사, 서니베일, 캘리포니아) ^ 미국 사우스캐롤라이나주 Rao, 연속 시스템의 진동(뉴욕): Wiley ^ Soedel, W., 1993, Vibrations of Shells and Plates, New York: Marcel Dekker Inc. (제2판) ^ Yu, Y.Y, 1996, Vibrations of Elastic Plates, New York: 스프링어 ^ Gorman, D., 1982, 암스테르담, 직사각형 판의 자유 진동 분석: 엘세비어 ^ Gorman, D.J., 1999, 중첩 방법에 의한 판의 진동 분석, 싱가포르: 월드 사이언티픽 ^ Rao, J.S., 1999, 뉴델리, 플레이트의 역학: 나로사 출판사 ^ Courant, Richard; Hilbert, David (1953), Methods of mathematical physics. Vol. I , Interscience Publishers, Inc., New York, N.Y., MR 0065391 「 」를 참조해 주세요. 

 플레이트 중앙 표면의 평면 내 변위,
플레이트 중앙 표면의 평면 내 변위, 플레이트 중앙 표면의 횡단(면 외) 변위,
플레이트 중앙 표면의 횡단(면 외) 변위,


 결과물은 면내 응력 α
결과물은 면내 응력 α






 재료의 포아송
재료의 포아송 



 플레이트의 벤딩 강성입니다.
플레이트의 벤딩 강성입니다.



![U=\int _{\Omega }[(\Delta w)^{2}+(1-\mu )(w_{{xx}}w_{{yy}}-w_{{xy}}^{2})]\,dx\,dy](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e05910527a998c2c018f56e396a389d247c2d3f)




![{\frac {1}{r}}{\frac {\partial }{\partial r}}\left[r{\frac {\partial }{\partial r}}\left\{{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)\right\}\right]=-{\frac {2\rho h}{D}}{\frac {\partial ^{2}w}{\partial t^{2}}}\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/60fb3502664cc9dd40b935ff5fe9f7c78ced6f83)


![{\frac {1}{\beta W}}\left[{\frac {d^{4}W}{dr^{4}}}+{\frac {2}{r}}{\frac {d^{3}W}{dr^{3}}}-{\frac {1}{r^{2}}}{\frac {d^{2}W}{dr^{2}}}+{\frac {1}{r^{3}}}{\frac {dW}{dr}}\right]=-{\frac {1}{F}}{\cfrac {d^{2}F}{dt^{2}}}=\omega ^{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5916e9e9ae9a8bae8941de20a2bd06932494400a)


![F(t)={\text{Re}}[Ae^{{i\omega t}}+Be^{{-i\omega t}}]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/5141832d05a388cee81f3b6e85b94e5f98a04005)



 첫 번째 종류의
첫 번째 종류의  첫 번째 종류의
첫 번째 종류의 






![w(r,t)=\sum _{{n=1}}^{\infty }C_{n}\left[J_{0}(\lambda _{n}r)-{\frac {J_{0}(\lambda _{n}a)}{I_{0}(\lambda _{n}a)}}I_{0}(\lambda _{n}r)\right][A_{n}e^{{i\omega _{n}t}}+B_{n}e^{{-i\omega _{n}t}}]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/20b230700283333b57568fed54812349cfe55ccb)



 이용하여 C
이용하여 C





![{\displaystyle \nabla ^{2}\nabla ^{2}w=w_{,1111}+2w_{,1212}+w_{,2222}=\left[{\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}\right]F(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb74394936f386e36e63191c2c8887c81efb4c6)

![{\displaystyle {\frac {D}{2\rho hW}}\left[{\frac {\partial ^{4}W}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}W}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}W}{\partial x_{2}^{4}}}\right]=-{\frac {1}{F}}{\frac {d^{2}F}{dt^{2}}}=\omega ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b541b52e01637cd2ee0ffbe36e0fc8e6be294c)
 독립되어 있고
독립되어 있고






 이전 표현과 비교한 결과 다음과 같은 방법으로 무한한 수의 솔루션을 얻을 수 있음을 알 수 있습니다.
이전 표현과 비교한 결과 다음과 같은 방법으로 무한한 수의 솔루션을 얻을 수 있음을 알 수 있습니다.


 구하려면 초기 조건과 푸리에 구성요소의 직교성을 사용합니다.예를 들어,
구하려면 초기 조건과 푸리에 구성요소의 직교성을 사용합니다.예를 들어,![{\displaystyle w(x_{1},x_{2},0)=\varphi (x_{1},x_{2})\quad {\text{on}}\quad x_{1}\in [0,a]\quad {\text{and}}\quad {\frac {\partial w}{\partial t}}(x_{1},x_{2},0)=\psi (x_{1},x_{2})\quad {\text{on}}\quad x_{2}\in [0,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b8bf04799103500c9924837d86fd48bc14b88cf)



