시누도

진동 곡선의 부등도 계산.

루즈 아르디덴의 높은 부신도의 산길의 레이서

쿠바 구마노 엠바르카데로의 굽이굽이 흐르는 리오 소작로가 가장 짧은 내리막길을 걷지 못하고 있다. 따라서, 그것의 부조화 지수는 1 이상이다.

같은 슬로프에서 상이한 점도의 스키 트랙 2개

적어도 하나의 변곡점이 있는 연속적으로 다른 곡선의 부등도, 부등도 지수 또는 부등도 계수는 곡선 끝점 사이의 곡선 길이(곡선을 따라)와 유클리드 거리(직선)의 비율이다. 이 치수 없는 수량은 "실제 경로 길이"를 곡선의 "가장 짧은 경로 길이"로 나눈 값으로 재인쇄할 수도 있다. 값은 1(직선의 경우)에서 무한(폐쇄 루프의 경우, 최단 경로 길이가 0이거나 한없이 긴 실제 경로의^[1] 경우)까지 다양하다.

해석

곡선은 양 끝 사이에 연속(점프 없음)이어야 한다. 선이 연속적으로 다를 때(각점 없음) 부조도 값은 정말로 유의하다. 양쪽 끝 사이의 거리는 연속 변곡점(순서 2의 점)을 통과하는 끊어진 선에 따른 복수의 세그먼트(segment)로 평가할 수도 있다.

경도의 계산은 3차원 공간(예: 소장의 중심축에 대하여)에서 종종 수행되지만(예: 소장의 중심축에 대하여)에서는 유효하다(이 때 선택한 평면에서의 곡선의 직교 투영 가능성, 수평면에서의 "고급" 경도, 수직면에서의 종단 경도).

부조화(예: 강/약)의 분류는 곡선(자세한 내용은 해안선 역설 참조)의 지도적 척도와 그 위를 흐르는 물체 속도(강, 눈사태, 자동차, 자전거, 봅슬레이, 스키어, 고속 열차 등)에 따라 달라지는 경우가 많다. 동일한 곡선선의 부조화는 매우 ss로 간주할 수 있다.고속 열차를 타려고 터벅터벅 걷다. 그러나 강에 타려고 하다. 그럼에도 불구하고, 몇 개의 강 굽이, 또는 몇몇 산길에서 끈의 연달아 매우 강한 부조화를 볼 수 있다.

주목할 만한 가치

다음 부등도 S:

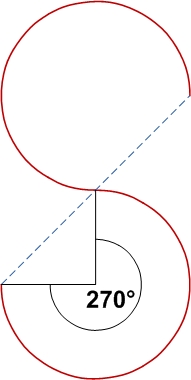
같은 평면에 위치한 2개의 반전 연속 반원형은 $S={\tfrac {\pi }{2}}\approx 1.5708...$ = $S={\tfrac {\pi }{2}}\approx 1.5708...$ $S={\tfrac {\pi }{2}}\approx 1.5708...$ 1 $S={\tfrac {\pi }{2}}\approx 1.5708...$ ${\displaystyle S={\tfrac {\pi }{2}}\약 1.5708...$ $S={\tfrac {\pi }{2}}\approx 1.5708...$ 원 반지름과 독립적이다.
사인 함수(반주기 정수 n에 걸쳐)는 해당 기간에 대한 사인 곡선의 arclength를 계산하여 계산할 수 있으며, $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ = 1 $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ + $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ (cos $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ ) $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ 6 $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ 216 $S=\textstyle {\tfrac {1}{n\pi }}\int _{0}^{n\pi }{\sqrt {1+(\cos x)^{2}}}dx\approx 1.216...$ ${\displaystyle S=\textstyle {1}{n\pi }\int _{0}^{n\pi }{\sqrt{1+(\cos x)^{2}}dx\ 약 1.216...$ $}$

270° 각도의 예

동일한 평면에 유사한 반대쪽 호 조인트가 있는 경우, 연속적으로 다를 수 있음:

중심각		시누도
도	라디안스	정확한	십진법
30°	${\frac {\pi }{6}$	${\frac {\pi }{3\\sqrt{6}-{\sqrt{2}}}}}$	1.0115
60°	${\frac {\pi }{3}}$	${\frac {\pi }{3}}$	1.0472
90°	${\frac {\pi }{2}}:$	${\frac {\pi }{2{\sqrt{2}}}$	1.1107
120°	${\frac {2\cdot \pi}{3}}$	${\frac {2\cdot \pi}{3{\sqrt{3}}}$	1.2092
150°	${\frac {5\cdot \pi}{6}}$	${\frac {5\cdot \pi}{33\sqrt{6}+{\sqrt{2}}:}}}}$	1.3552
180°	$\displaystyle \pi }$	${\frac {\pi }{2}}:$	1.5708
210°	${\frac {7\cdot \pi}{6}}$	${\frac {7\cdot \pi}{33\sqrt{6}+{\sqrt{2}}:}}}}$	1.8972
240°	${\frac {4\cdot \pi}{3}}$	${\frac {4\cdot \pi}{3{\sqrt{3}}}$	2.4184
270°	${\frac {3\cdot \pi}{2}$	${\frac {3\cdot \pi}{2{\sqrt{2}}$	3.3322
300°	${\frac {5\cdot \pi}{3}}$	${\frac {5\cdot \pi}{3}}$	5.2360
330°	${\frac {11\cdot \pi}{6}}$	${\frac {11\cdot \pi}{33\sqrt{6}-{\sqrt{2}}}}}}$	11.1267

리버스

강에 대한 연구에서 점성 지수는 위에서 제시한 일반적인 형태와 유사하지만 동일하지는 않다. 이는 다음과 같다.

{\text{SI}}={\frac {\text{channel length}{\text{downvalley length}}}}}}}

일반적인 형태와의 차이는 다운밸리 경로가 완벽하게 직선적이지 않기 때문에 발생한다. 부등도 지수는 최대 하강 방향으로 정의된 경로로부터의 편차로 설명할 수 있다. 이 때문에 직하류로 흘러가는 암반하류는 점성지수가 1이고, 굽이치는 하천은 점성지수가 1보다 큰 점성지수가 있다.^[2]

또한 선상에 흐르는 하천이 종단 사이의 거리를 물리적으로 이동할 수 없었던 경우를 구별할 수 있다: 일부 유압 연구에서는, 기울기 각도가 달라도 수평 직진 투영을 따라 암반 위를 흐르는 급류에 대해 1의 점성 값을 할당한다.

강의 경우, 상투성 등급인 SI는 다음과 같다.

SI <1.05: 거의 직선
1.05 ≤ SI < 1.25: 권선
1.25 ≤ SI <1.50: 비틀림
1.50 ≤ SI: 굽실거림

하천형상은 평균 부등도(채널 길이가 아닌 출처-입구 거리로 측정)를 $π$ 으로 하는 자가조직체계의 지배를 받는다고 주장되어 왔으나,^[3] 이후 연구에서는 이 문제를 해결하지 못하여 평균 값이 2 미만이었다.^[4]

참고 항목

참조

^ 레오폴드, 루나 B, 월만, M.G.와 밀러, J.P., 1964, W.H. 프리먼과 Co., 522p.의 유체적 과정.
^ Mueller, Jerry (1968). "An Introduction to the Hydraulic and Topographic Sinuosity Indexes1". Annals of the Association of American Geographers. 58 (2): 371. doi:10.1111/j.1467-8306.1968.tb00650.x.
^ Stølum, Hans-Henrik, "River Meandering as a Self-Organization Process", Science, 271 (5256): 1710–1713, Bibcode:1996Sci...271.1710S, doi:10.1126/science.271.5256.1710.
^ Grime, James (March 14, 2015), "A meandering tale: the truth about pi and rivers", Alex Bellos's Adventures in Numberland, The Guardian.

[1] 레오폴드, 루나 B, 월만, M.G.와 밀러, J.P., 1964, W.H. 프리먼과 Co., 522p.의 유체적 과정.

[2] Mueller, Jerry (1968). "An Introduction to the Hydraulic and Topographic Sinuosity Indexes1". Annals of the Association of American Geographers. 58 (2): 371. doi:10.1111/j.1467-8306.1968.tb00650.x.

[3] Stølum, Hans-Henrik, "River Meandering as a Self-Organization Process", Science, 271 (5256): 1710–1713, Bibcode:1996Sci...271.1710S, doi:10.1126/science.271.5256.1710.

[4] Grime, James (March 14, 2015), "A meandering tale: the truth about pi and rivers", Alex Bellos's Adventures in Numberland, The Guardian.

[1]

[2]

[3]

[4]

v t 하천형태학
대규모 피쳐	충적평야 배수분지 배수 시스템(지형물학) 하구 스트라흘러 번호(스트림 순서) 리버밸리 강 삼각주 강의 부신도
충적하천	아나브란치 애벌전(강) 막대(하천 형태학) 땋은 강 채널 패턴 컷 뱅크 플러드플레인 므안데르 므안데르 컷오프 마우스 바 옥소보우호 포인트 바 리플 래피즈 리파리아 지역 강 분기 하천수역이동 하구 슬립 오프 슬로프 스트림 풀 탈웨그
베드록 강	협곡 틱포인트 덤프 풀
베드폼	에이트 안티두네 둑 전류 리플
지역 프로세스	아그분해 기준레벨 분해(지질학) 침식 및 구조론 하천회생
역학	증착(지질학) 물침식 엑너 방정식 해크의 법칙 헬리코이드 흐름 플레이페어의 법칙 침전물 수송 방향을 반대로 한 하천 목록
카테고리 포털

Search

시누도

네임스페이스

더

목차

해석

주목할 만한 가치

리버스

참고 항목

참조