셸림프룩 원리

이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2013년 6월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

Scheimpflug 원리는 렌즈 평면이 영상 평면에 평행하지 않을 때 초점 평면의 방향, 렌즈 평면, 광학 시스템의 영상 평면(카메라 등) 사이의 기하학적 관계에 대한 설명이다. 그것은 뷰 카메라에서 일부 카메라 움직임의 사용에 적용된다. 각막 지형의 매핑인 각막 파치메트리에도 사용하는 원리로 라식 등 굴절 안과 수술에 앞서 행하며 각막의 조기 발견에도 사용된다. 이 원리는 오스트리아 육군 대장 테오도르 셰임프플룩의 이름을 따서 명명되었는데, 셰임프플룩 대위는 스스로 쥘 카펜티어에게 이 규칙을 인정하여 스티글러의 에포니미 법칙의 본보기로 삼았지만, 항공 사진의 원근법 왜곡을 교정하기 위한 체계적 방법과 장치를 고안하는데 사용했다.

설명

보통 카메라의 렌즈와 이미지(필름 또는 센서) 평면은 평행하고 초점면(PoF)은 렌즈와 이미지 평면에 평행하다. 평면 피사체(건물 측면 등)도 영상 평면에 평행하면 PoF와 일치할 수 있으며 피사체 전체를 날카롭게 렌더링할 수 있다. 실험 평면이 영상 평면에 평행하지 않은 경우 그림 1에서와 같이 PoF와 교차하는 선을 따라서만 초점이 맞춰진다.

그러나 렌즈가 영상 평면에 대해 기울어졌을 때, 이미지 평면에서 확장된 비스듬한 접선과 렌즈 평면에서 확장된 또 다른 접선은 그림 2와 같이 PoF도 통과하는 선에서 만난다. 이 조건으로 영상 평면에 평행하지 않은 평면 피사체는 완전히 초점이 맞춰질 수 있다. 많은 사진작가들이 PoF와 렌즈 평면, 필름 평면 사이의 정확한 기하학적 관계를 알지 못하고 있는 동안, 1800년대 중반부터 PoF를 흔들고 기울이기 위해 렌즈를 흔들고 기울이는 연습을 했다. 그러나 카펜티어와 셸림프플룩이 공정을 자동화할 수 있는 장비를 생산하고자 할 때, 그들은 기하학적 관계를 찾을 필요가 있었다.

Scheimpflug(1904)은 그의 영국 특허에서 이 개념을 언급했고, Carpentier(1901)는 원근법 보정 사진 확대기에 대한 초기 영국 특허에서도 이 개념을 설명했다. 그 개념은 Gérard Desarges의 투영 기하학의 정리로부터 유추될 수 있다. 또한 그 원리는 Schempflug 원리의 Proof of the Sheimpflug 원리에 나타난 바와 같이 가우스 얇은 렌즈 공식의 단순한 기하학적 고려와 적용에서 쉽게 파생된다.

초점 평면 변경

렌즈와 영상 평면이 평행하지 않을 때 초점^[a] 조정은 렌즈 축을 따라 단순히 치환하는 것이 아니라 PoF를 회전시킨다. 회전축은 그림 3과 같이 렌즈 전면 초점면과 이미지 평면에 평행한 렌즈 중심을 통과하는 평면의 교차점이다. 영상 평면이 IP에서₁ IP로₂ 이동하면 PoF가 위치 PoF에서₁ 위치 PoF로₂ 축 G를 중심으로 회전하며, "Schempflug line"이 위치 S에서₁ 위치 S로₂ 이동한다. 회전축은 "카운터 축" (Schimmflug 1904), "힌지 선" (Merklinger 1996), "피봇 포인트"(휠러)라는 많은 다른 이름이 붙여졌다.

초점 길이의 렌즈가 있는 경우 그림 4를 참조하십시오. f 비스듬히 기울어지다 θ 영상 평면에 상대적인 거리 J^[b] 렌즈 중심에서 축 G까지 는 다음과 같이 주어진다.

${\displaystyle J={\frac {f}{\sin \theta }}.}$

만약 v′ 영상 평면에서 렌즈 중앙까지의 시선선을 따라 각도를 나타내는 거리 ψ 이미지 평면과 PoF 사이에 다음이^[c] 주어진다.

${\displaystyle \tan \cHB ={\frac {v'}{v'\cos \theta -f}\sin \theta .}$

동등하게, 렌즈의 물체 측에서, 다음과 같은 경우. u′ 렌즈의 중심에서 PoF까지 시선선을 따라 각도를 이루는 거리 ψ 에 의해 주어지다

${\displaystyle \tan \cHB ={\frac {u'}{f}}\sin \theta .}$

각도 ψ 초점 거리에 따라 증가한다. 포커스가 무한대에 있을 때, PoF는 0이 아닌 기울기 값에 대해 영상 평면에 수직이다. 거리 u′ 그리고 v′ 시야를 따라 물체와 이미지 거리가 아니다. u 그리고 v 박음식에 쓰이는.

${\displaystyle {\frac {1}{u}+{\frac {1}{v}={\frac {1},}$

거리가 렌즈 평면에 수직인 경우. 거리 u 그리고 v 시야 거리 기준 = cos 및 = cos와 관련이 있다.

평면 피사체의 경우, 카메라에서 평탄한 지형에서 수 마일 동안 확장되는 도로와 같이, 기울기를 설정하여 실험 평면에 축 G를 배치하고 포커스를 조정하여 실험 평면과 일치하도록 PoF를 회전시킬 수 있다. 영상 평면에 평행하지 않더라도 피사체 전체가 초점이 맞춰질 수 있다.

초점면도 회전하여 실험면과 일치하지 않고, 대상의 작은 부분만 초점에 있도록 할 수 있다. 이 기법은 실제로는 셸림프럭 원리에 의존하지만, 때때로 "안티-스킴프럭"이라고 불린다.

초점 평면의 회전은 렌즈 평면 또는 영상 평면을 회전하여 수행할 수 있다. 렌즈를 돌리면(뷰 카메라의 전면 표준을 조정하여) 건물의 면과 같은 평면 피사체에서 선형^[d] 원근법이 바뀌지 않지만, 광택을 피하기 위해 영상 원이 큰 렌즈가 필요하다. 영상 평면을 회전하면(뷰 카메라에서 후면 또는 후면 표준을 조정하여) 원근법이 변경되지만(예: 건물의 측면은 수렴) 영상 원이 작은 렌즈와 함께 작동한다. 렌즈나 등을 수평축을 중심으로 회전하는 것을 흔히 틸트라고 하며, 수직축을 중심으로 회전하는 것을 흔히 스윙이라고 한다.

카메라 이동

틸트 및 스윙은 대부분의 뷰 카메라에서 사용 가능한 움직임으로, 종종 전면과 후면 표준 모두에서, 그리고 일부 중소형 카메라에서는 뷰 카메라 움직임을 부분적으로 모방하는 특수 렌즈를 사용한다. 그러한 렌즈는 흔히 틸트 시프트(tilt-shift) 또는 "내성적 제어(^[e]contractive control 일부 카메라 모델의 경우 제조업체의 일반 렌즈 중 일부와 이동이 가능한 어댑터가 있으며, '렌즈베이비' 또는 '프리렌징'과 같은 부착물을 사용하여 조잡한 근사치를 얻을 수 있다.

필드 깊이

렌즈와 영상 평면이 평행할 때, 필드 깊이(DoF)는 초점 평면의 양쪽에 있는 평행 평면 사이에 확장된다. Scheimpflug 원칙을 채택하면 그림 5와 같이 ^[g]DoF는 그림 5와 같이 PoF 회전 축에서 쐐기의 정점을 갖는 ^[f]쐐기 모양의 (Merklinger 1996, 32; Tillmanns 1997, 71)가 된다. DoF는 정점에 0이며 렌즈 시야의 가장자리에서 얕게 유지되며 카메라와의 거리에 따라 증가한다. 카메라 근처의 얕은 DoF는 가까운 물체를 날카롭게 렌더링하려면 PoF를 주의 깊게 배치해야 한다.

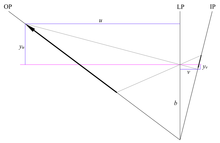
영상 평면에 평행한 평면에서 DoF는 PoF 위와 아래로 균등하게 분포한다. 그림 5에서 거리는 y_n 그리고 y_f 비행기에서 VP는 동일하다. 이 분포는 PoF에 대한 최적의 위치를 결정하는 데 도움이 될 수 있다. 한 장면에 원거리 장신 피쳐가 포함된 경우, 장면에 DoF를 가장 잘 맞추는 것은 종종 PoF가 해당 피쳐의 수직 중간점을 통과하도록 하는 데서 비롯된다. 그러나 각 DoF는 PoF에 대해 균등하게 분포되지 않는다.

거리 y_n 그리고 y_f (Merklinger 1996, 126)에 의해 주어진다.

${\displaystyle y_{x}={\frac {f}{v'}}{\frac {u'}{u}}}{\mathrm {h}{}}}}}}$

어디에 f 렌즈 초점 길이, v′ 그리고 u′ 이미지 및 물체 거리가 가시선과 평행한가? u_h 초초점 거리인데 J 렌즈 중심에서 PoF 회전 축까지의 거리. 황갈색에 대한 이미지 측 방정식을 해결함으로써 v′ 대신하여 v′ 그리고 u_h 위의 방정식에서 값은 다음과 같이 동등하게 주어질 수 있다.^[h]

${\displaystyle y_{x}={\frac {Cnc}{f}}\좌측({\frac {1}{\tan \tan \tan \psi }{1}{\tan \psi }우측)\}$

어디에 N 렌즈 -숫자 및 c 혼란의 원이다. 큰 초점 거리(PoF와 영상 평면 사이의 큰 각도와 동일), ≈ 및 (Merklinger 1996, 48)^[i]

${\displaystyle y_{x}\약간 {\frac {u'}{u}}}{{u}}}}{\mathrm {h}}J\}$

또는

${\displaystyle y_{x}\약 {\frac {Cnc}{f}{f}}{\frac {u'}{\tan \}\,}$

따라서 초초점 거리에서는 영상 평면에 평행한 평면의 DoF가 다음과 같은 거리를 연장한다. J 포프 양쪽에

풍경화 등 일부 피사체가 있는 경우 쐐기 모양의 도프(DoF)가 현장에 잘 맞고, 더 작은 렌즈로 만족스러운 선명도를 얻을 수 있는 경우가 많다. f-PoF가 영상 평면에 평행할 경우 필요한 수보다 많은 수(더 큰 구멍)

선택초점

날카로움의 영역은 또한 큰 기울기와 작은 f-숫자를 사용하여 매우 작게 만들 수 있다. 예를 들어 소형 카메라의 경우 90mm 렌즈에 8° 기울이면 초초점 거리에서의 총 수직 DoF는 대략적으로^[j]

${\displaystyle 2J=2{\frac {f}{\sin \theta }}2\time {\frac {90{\text{mm}}{\sin 8^{\circle }}}=1293{\text{mm}\,\,}\,\,}\,},},.}$

f/2.8의 개구부, 0.03 mm의 혼동 원과 함께, 이것은 대략 u의 거리에서 발생한다.

${\displaystyle {\frac{f^{2}}:{Cnc}={\frac {90^{2}}:{2}.8\cHB 0.03}=96.4{\text{m}\,}$

물론 기울기는 PoF의 위치에도 영향을 미치기 때문에 날카로움의 영역을 최소화하기 위해 기울기를 선택하면 PoF가 임의로 선택한 지점을 두 개 이상 통과하도록 설정할 수 없다. PoF가 둘 이상의 임의 지점을 통과하려면 기울기와 포커스가 고정되며, 렌즈 f-숫자만이 날카로움을 조절할 수 있다.

공식의 파생

셸림프룩 원리의 증거

2차원 표현에서 렌즈 평면으로 기울어진 물체 평면은 다음과 같이 기술된 선이다.

${\displaystyle y_{}}$ ${\displaystyle u_{}}$= ${\displaystyle u}$+ ${\displaystyle b}$ ${\displaystyle y_{u}=au+b}$ $$.

광학 규약에 의해 물체와 영상 거리 모두 실제 영상에 대해 양수적이므로 그림 6에서 물체 거리 u는 렌즈 평면 LP의 왼쪽으로 증가한다; 수직 축은 광학 축 위 값과 광학 축 아래 값이 음수인 일반 데카르트 규약을 사용한다.

물체 거리 u, 영상 거리 v 및 렌즈 초점 길이 f 사이의 관계는 얇은 렌즈 방정식에 의해 주어진다.

${\displaystyle {\frac{1}{u}+{\frac {1}{v}={\frac {1},;}$

너를 위한 해결은 주는 것이다.

${\displaystyle u={\frac {vf}{v-f}\}$

하도록

${\displaystyle y_{}{u}_{}}$ = ${\displaystyle v}$ ${\displaystyle \frac{}{}}$ -${\displaystyle \frac{}{}}$f${\displaystyle \frac{}{}}$+ ${\displaystyle b}$ ${\displaystyle y_{u}=a\,{\frac {vf}{v-f}}+b}$ $$.

확대 m은 영상 높이 y_v 대 물체 높이 y의_u 비율이다.

${\displaystyle m={\frac {y_{v}}{y_{u}}\,;}$

y와_u y는_v 반대 의미여서 확대는 음수(-)로 반전된 영상을 나타낸다. 그림 6의 유사한 삼각형에서 확대는 또한 이미지 및 물체 거리를 연관시켜 다음과 같이 한다.

${\displaystyle m}$=${\displaystyle }$- ${\displaystyle v\frac{}{}}$ ${\displaystyle \frac{u}{}}$=${\displaystyle }$- ${\displaystyle \frac{v}{}}$- ${\displaystyle \frac{}{}}$ ${\$

렌즈의 이미지 측면에

${\displaystyle{\fline}y_{v}&=my_{u}\\\-{\frac {v-f}{f}{v-f}+b\right)\&#=\&#(av+{v}{frac{f-b\right}}}}}}}}}\{ligineed}}}}}}}}}}}}}}}$

부여

${\displaystyle {}_{}\frac{y}{}}$ ${\displaystyle v_{}}$=${\displaystyle }$- (${\displaystyle }$( +${\displaystyle b\frac{}{}}$ )${\displaystyle v}$ + ${\displaystyle b}$ + b + b = ${\displaystyle y_{v}=-\왼쪽(a+{\frac$ {$b}}{f}\오른쪽)v+b}$ $$.

경사 객체 평면의 초점 위치는 평면이다. 2차원 표현에서 y 절편은 객체 평면을 설명하는 선의 그것과 동일하므로 객체 평면, 렌즈 평면 및 영상 평면은 공통 교차점을 가진다.

유사한 증거는 Larmore(1965, 171–173)에 의해 제시된다.

영상 평면과 PoF 각도

그림 7부터,

${\displaystyle \tan \cHB ={\frac {u'+v'}{S}\...}$

어디에 u′ 그리고 v′ 물체와 이미지 거리가 가시선을 따라 있는지 여부 S 시선에서 S의 Scheimpflug 교차로까지의 거리. 다시 그림 7에서,

${\displaystyle \tan \tan \tan \theta ={\frac {v'}{S}\,;}$

앞의 두 방정식을 합치면

$\\displaystyle \tan \tan \tan \tan \{\frac {u'}{v'}+1\right)\tan \tan \theta \,}$

얇은 렌즈 방정식으로 보면

${\displaystyle {\frac {1}{u}}+{\frac {1}{v}={\frac {1}{v}\cos \cos \theta }}}{\frac {1}{f}\, \cos }}},}$

해결 방법 u′ 주다

${\displaystyle u'={\frac {v'f}{v'\cos \theta -f}\,;}$

이 결과를 황갈색 주기의 방정식으로 대체하다.

${\displaystyle \tan \tan =\left\fac {f}{v'\cos \cos \theta ={\flac {f+v'\cos \cos \v' -f}\tan \theta \cos \f}$

또는

${\displaystyle \tan \cHB ={\frac {v'}{v'\cos \theta -f}\sin \theta \,}$

마찬가지로, 얇은 렌즈 방정식은 다음에 대해 해결할 수 있다. v′, 그리고 그 결과는 황갈색에 대한 방정식으로 대체되어 물체측 관계를 갖게 되었다.

${\displaystyle \tan \cHB ={\frac {u'}{f}}\sin \theta \,}$

에 주목하여

${\displaystyle {\frac {u'}{f}}={\frac {u}{f}}{\frac {1}{\cos \cos }}={\frac {m+1}{m}{\frac {1}{\cos \tea }}}$

사이의 관계 ψ 그리고 θ 확대된 면으로 표현할 수 있다. m 시야에 들어오는 물체의:

${\displaystyle \tan \cHB ={\frac {m+1}{m}}\tan \theta \,}$

"힌지 규칙"의 증거

그림 7부터,

${\displaystyle \tan \psi ={\frac {u'}{J}\,;}$

객체 측면의 이전 결과와 결합하여 제거 ψ 주다

${\displaystyle \sin \theta ={\frac {f}{J}\,}$

다시 그림 7에서,

${\displaystyle \sin \theta ={\frac {d}{J}\}}$

그래서 거리 d 렌즈 초점 길이, f그리고 지점 G는 이미지 평면에 평행한 선이 있는 렌즈의 전면 초점 평면에 교차점에 있다. 거리 J 렌즈 기울기와 렌즈 초점 길이에만 의존한다. 특히, 초점의 변화에 영향을 받지 않는다. 그림 7부터,

${\displaystyle \tan \tan \theta ={\frac {v'}{S}\}$

그래서 S에서 Scheimpflug 교차로까지의 거리는 초점이 변경됨에 따라 달라진다. 따라서 포커스가 조정될 때 PoF는 G에서 축을 중심으로 회전한다.

메모들

참조

• 카펜티어, 줄스 1901. 카메라 확대 또는 유사 카메라의 개선. GB특허 1139호. 1901년 1월 17일 접수, 1901년 11월 2일 발행. 다운로드 가능(PDF).
• 1965년 루이스 라모어 사진 원리 소개. 뉴욕: 도버 출판사, 주식회사.
• Merklinger, Harold M. 1996. 뷰 카메라 포커스를 맞추십시오. 베드포드, 노바스코샤: 해안 인쇄 유한회사. ISBN0-9695025-2-4. 다운로드 가능(PDF).
• 셸림프룩, 테오도르. 1904. 사진 및 기타 목적을 위한 렌즈와 거울의 수단에 의한 평면 사진 및 이미지의 체계적 변경 또는 왜곡을 위한 방법 및 장치 개선. GB특허 1196번. 1904년 1월 16일 접수, 1904년 5월 12일 발행. 다운로드 가능(PDF).
• 틸먼, 1997년 우르스 크리에이티브 대형 포맷: 기본 및 응용 프로그램. 2부. 스위스 푸에르탈렌: 시나르 AG. ISBN 3-7231-0030-9
• Steger, Carsten (2017). "A Comprehensive and Versatile Camera Model for Cameras with Tilt Lenses". International Journal of Computer Vision. 123: 121–159. doi:10.1007/s11263-016-0964-8.

외부 링크

위키미디어 커먼즈에는 Scheimpflug 원칙과 관련된 미디어가 있다.

• Leonard Evens의 카메라 지오메트리 보기(PDF). 타원형 흐릿점이 DoF에 미치는 영향 분석
• Leonard Evens의 기울어진 렌즈 필드 깊이(PDF) View 카메라 지오메트리에 대한 보다 실용적이고 접근성 높은 요약
• Quang-Tuan Luong의 뷰 카메라 포커스 방법. 초점 평면을 설정하는 방법에 대한 토론 포함
• 해롤드 머클링거의 셸림플뤼그 원리
• Harold Merklinger의 View 카메라 포커스에 대한 부록(PDF)
• Ram Subramanian이 인간 눈의 숙박역학 연구(PDF)를 위한 일방적 실시간 Schempflug 비디오그래피
• Robert Wheeler의 View Camera 지오메트리(PDF)에 대한 참고 사항
• 틸트 및 시프트 렌즈: 소형 틸트 시프트 렌즈에 맞춤 제작, 모든 형식에 원칙 적용