불변 질량
Invariant mass불변질량, 정지질량, 고유질량, 적정질량 또는 결합계통의 경우 단순히 계의 전체 운동과 무관한 물체 또는 물체의 총질량의 부분이다.보다 정확하게는 로렌츠 [1]변환과 관련된 모든 기준 프레임에서 동일한 시스템 총 에너지 및 운동량의 특성입니다.시스템에 대해 모멘텀 중심 프레임이 존재하는 경우, 시스템의 불변 질량은 "휴대 프레임"의 총 질량과 동일합니다.시스템의 운동량이 0이 아닌 다른 기준 프레임에서는 시스템의 총 질량(상대론적 질량)이 불변 질량보다 크지만 불변 질량은 변하지 않는다.
질량-에너지 등가성 때문에 시스템의 나머지 에너지는 단순히 불변 질량 곱하기 빛의 속도 제곱이다.마찬가지로, 시스템의 총 에너지는 총 질량(상대론적)에 빛의 속도를 곱한 값입니다.
4개의 모멘텀이 늘 벡터인 시스템(예를 들어 단일 광자 또는 정확히 동일한 방향으로 이동하는 많은 광자)은 불변 질량이 0이며 무질량이라고 한다.빛의 속도보다 더 빠르게 움직이는 물리적 물체나 입자는 우주와 같은 4개의 운동(예: 가설의 타키온)을 가지며, 이러한 운동들은 존재하지 않는 것으로 보인다.모든 시간 형태의 4차원 모멘텀은 모멘텀 프레임의 중심인 모멘텀(3차원)이 0인 기준 프레임을 가지고 있습니다.이 경우, 불변 질량은 양이고 나머지 질량을 말합니다.
시스템 내의 물체가 상대적인 운동을 하고 있는 경우, 전체 시스템의 불변 질량은 물체의 정지 질량의 합계와 다릅니다.이 값은 시스템의 총 에너지를 c로2 나눈 값과도 같습니다.질량의 정의에 대한 설명은 질량-에너지 등가성을 참조한다.시스템의 질량은 전체 시스템이 0인 운동량 프레임의 중심에서 무게 또는 질량 척도로 측정해야 하므로 이러한 척도는 항상 시스템의 불변 질량을 측정합니다.예를 들어, 저울은 병의 불변 질량의 일부가 되는 가스병에 있는 분자의 운동 에너지를 측정할 수 있으며, 따라서 그 나머지 질량도 측정할 수 있다.이러한 시스템의 무질량 입자에 대해서도 마찬가지이며, 이러한 입자의 에너지에 따라 시스템에 불변 질량을 더하고 정지 질량을 더합니다.
고립된 거대 시스템의 경우, 시스템의 질량 중심은 일정한 준휘도 속도로 직선으로 이동합니다(보기에 사용되는 기준 프레임에 따라 속도가 다릅니다).따라서 관찰자는 항상 관찰자와 함께 이동하도록 배치할 수 있습니다.모멘텀의 중심 프레임인 이 프레임은 총 운동량이 0이며, 결합계(가스병 등)인 경우에는 시스템 전체가 '정지 상태'라고 생각할 수 있다.이러한 가정 하에 존재하는 이 프레임에서는 시스템의 불변 질량은 총 시스템 에너지(제로 모멘텀 프레임 내)를 c로 나눈2 값과 같습니다.운동량 프레임의 중심에 있는 이 총 에너지는 다양한 관성 프레임에서 다양한 관찰자가 볼 때 시스템이 가질 수 있는 최소 에너지이다.
위의 이유로 이러한 정지 프레임은 단일 광자 또는 한 방향으로 이동하는 광선에는 존재하지 않습니다.그러나 두 개 이상의 광자가 서로 다른 방향으로 이동하는 경우 질량 프레임의 중심(또는 시스템이 묶여 있는 경우 "휴대 프레임")이 존재합니다.따라서, 서로 다른 방향으로 이동하는 여러 광자의 시스템의 질량은 양수이며, 이것은 각 광자에 대해 존재하지 않더라도 이 시스템에 대해 불변 질량이 존재한다는 것을 의미한다.
정지 질량의 합계
시스템의 불변 질량은 운동량 프레임의 중심에 남아 있는 시스템 구성 요소의 운동 에너지 질량을 포함하므로, 시스템의 불변 질량은 개별 구성 요소의 불변 질량(정지 질량)의 합보다 클 수 있습니다.예를 들어, 정지 질량과 불변 질량은 시스템의 불변 질량에 질량을 더할 수 있지만 개별 광자의 경우 0이다.이러한 이유로 불변 질량은 일반적으로 첨가량이 아니다(전위 또는 운동에너지가 없는 시스템의 거대한 입자가 총 질량에 추가될 수 있는 드문 상황이 몇 가지 있지만).
물체 A가 처음에 정지해 있는 다른 물체 B를 향해 이동하는 2체 시스템의 단순한 경우를 생각해 보자(특정 기준 프레임에서).이 2체 시스템의 불변 질량의 크기(아래 정의 참조)는 정지 질량의 합계와 다르다(즉, 정지 시 각각의 질량).순운동량이 0인 모멘텀 프레임에서 동일한 시스템을 고려하더라도 시스템의 불변 질량의 크기는 그 안에 있는 입자의 나머지 질량의 합계와 같지 않습니다.
이러한 입자의 운동 에너지와 힘장의 위치 에너지는 총 에너지를 입자 정지 질량의 합 이상으로 증가시키며, 두 항 모두 시스템의 불변 질량에 기여합니다.관측자가 계산한 입자 운동 에너지의 합계는 운동량 프레임의 중심에서 가장 작습니다(시스템이 결합되어 있는 경우 "휴면 프레임"이라고 함).
그들은 또한 종종 하나 이상의 기본 힘을 통해 상호작용을 하게 되고, 상호작용의 잠재적 에너지를 그들에게 제공합니다. 아마도 부정적일 수 있습니다.
고립된 거대 시스템의 경우 질량 중심은 일정한 광속 이하의 속도로 직선으로 이동합니다.따라서 관찰자는 항상 관찰자와 함께 이동하도록 배치할 수 있습니다.운동량 프레임의 중심인 이 프레임에서는 총 운동량이 0이며, 결합계(가스병 등)인 경우 시스템 전체가 "정지 상태"로 간주될 수 있습니다.항상 존재하는 이 프레임에서 시스템의 불변 질량은 총 시스템 에너지(제로 모멘텀 프레임 내)를 c로 나눈2 값과 같습니다.
입자물리학에서 정의된 바와 같이
입자물리학에서 불변질량0 m은 입자의 나머지 프레임의 질량과 같으며, 입자의 에너지 E와 모든 프레임에서 측정된 운동량 p에 의해 에너지-모멘텀 관계에 의해 계산될 수 있습니다.
이 불변 질량은 모든 기준 프레임에서 동일하다(특수 상대성 이론 참조).이 방정식은 불변 질량이 공간과 시간 차원에 대해 다른 부호를 가진 상대론적 버전의 피타고라스 정리를 사용하여 계산되는 4벡터의 유사 유클리드 길이(E, p)라고 말한다.이 길이는 벡터의 통상적인 길이가 회전할 때 유지되는 것과 마찬가지로 로렌츠 부스트 또는 4차원 회전에서도 유지됩니다.양자 이론에서 불변 질량은 소립자에 대한 상대론적 디락 방정식의 변수이다.Dirac 양자 연산자는 입자 4모멘텀 벡터에 해당합니다.
불변질량은 붕괴시 보존되는 양에서 결정되기 때문에 단일 입자의 붕괴생성물의 에너지와 운동량을 이용하여 계산되는 불변질량은 붕괴된 입자의 질량과 같다.입자 시스템의 질량은 일반 공식에서 계산할 수 있습니다.
- W는 입자계의 불변 질량으로 붕괴 입자의 질량과 같습니다.
- ∙ \ E는 입자의 에너지의 합계입니다
- \는 입자의 운동량의 벡터 합이다(모멘타의 크기와 방향 모두 동일
불변질량이라는 용어는 비탄성 산란 실험에서도 사용된다.총 유입 에너지가 검출된 총 에너지보다 클 경우(즉, 실험에서 모든 방출 입자가 검출되지 않음), 반응의 불변 질량('결손 질량'이라고도 함) W는 다음과 같이 정의된다(자연 단위).
만약 실험 중에 검출되지 않은 지배입자가 하나 있다면, 불변질량의 그래프는 누락된 입자의 질량에 날카로운 피크를 보여줄 것이다.
한 방향의 운동량을 측정할 수 없는 경우(즉, 중성미자의 경우 누락된 에너지로부터만 유추됨) 가로 질량을 사용한다.
예: 2 입자 충돌
2 입자 충돌(또는 2 입자 붕괴)에서 불변 질량의 제곱(자연 단위)은 다음과 같다.
무질량 입자
모멘타가 각도(\를 형성하는 두 개의 질량 없는 입자로 구성된 시스템의 불변 질량은 다음과 같은 편리한 식을 가집니다.
충돌기 실험
입자충돌기 실험에서는 입자의 각도 위치를 와 로 정의하는 경우가 많다. 또한 T 는 보통 측정됩니다.이 경우 입자가 질량이 없거나 매우 상대론적( m\ Em 이라면 불변 질량은 다음과 같습니다.
휴식 에너지
입자의 나머지 0은 다음과 같이 정의됩니다.
휴식 에너지의 개념은 에너지와 질량의 동등성에 대한 아인슈타인의 유명한 결론으로 이끈 특수 상대성 이론에서 따랐습니다.질량-에너지 등가성은 배경을 참조한다.
「 」를 참조해 주세요.
레퍼런스
- Landau, L.D.; Lifshitz, E.M. (1975). The Classical Theory of Fields: 4-th revised English Edition: Course of Theoretical Physics Vol. 2. Butterworth Heinemann. ISBN 0-7506-2768-9.
- Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.
인용문
- ^ 로렌스 S.러너.과학자와 엔지니어를 위한 물리학, 제2권, 1073쪽. 1997년.
- ^ Phillip L. Reu (March 2007). Development of the Doppler Electron Velocimeter—Theory (PDF) (Report). Sandia National Laboratories. SAND2006-6063. Archived from the original (PDF) on 2015-06-23.
- ^ Modell, Michael; Reid, Robert C. (1974). Thermodynamics and Its Applications. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-914861-2.
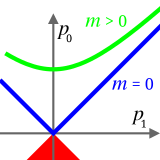



 입자계의 불변 질량으로 붕괴 입자의 질량과 같습니다.
입자계의 불변 질량으로 붕괴 입자의 질량과 같습니다.
 입자의 운동량의
입자의 운동량의 

 형성하는 두 개의 질량 없는 입자로 구성된 시스템의 불변 질량은 다음과 같은 편리한 식을 가집니다.
형성하는 두 개의 질량 없는 입자로 구성된 시스템의 불변 질량은 다음과 같은 편리한 식을 가집니다.![{\displaystyle {\begin{aligned}M^{2}&=(E_{1}+E_{2})^{2}-\left\|{\textbf {p}}_{1}+{\textbf {p}}_{2}\right\|^{2}\\&=[(p_{1},0,0,p_{1})+(p_{2},0,p_{2}\sin \theta ,p_{2}\cos \theta )]^{2}\\&=(p_{1}+p_{2})^{2}-p_{2}^{2}\sin ^{2}\theta -(p_{1}+p_{2}\cos \theta )^{2}\\&=2p_{1}p_{2}(1-\cos \theta ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e86c0b0553acbe9c6e2db880847c2a04257a0dbf)





 다음과 같이 정의됩니다.
다음과 같이 정의됩니다.



