4등분
Quadrisecant기하학에서 공간 곡선의 4등분선 또는 4등분선은 곡선의 4점을 통과하는 선입니다.이것은 일반적인 공간 곡선이 선과 함께 가질 수 있는 가능한 가장 큰 교차점 수이며, 이러한 곡선의 경우 4층계가 별개의 선 집합을 형성합니다.4상자는 몇 가지 유형의 곡선에 대해 연구되었다.
- 매듭이론에서 매듭과 고리는 중요하지 않을 때 항상 4상자를 가지며, 4상자의 존재와 수는 매듭의 최소 총 곡률 및 로프 길이를 포함한 매듭 불변성과 관련하여 연구되어 왔다.
- 복잡한 투영 공간에서 비단수 대수 곡선의 4등분 수는 Arthur Cayley가 도출한 공식으로 계산할 수 있다.
- 스큐선 배열의 4상자는 배열에서 4선 서브셋에 접촉한다.이러한 구성에는 규칙 표면과 슐레플리 더블 6 구성이 관련되어 있습니다.
정의와 동기 부여
사등각선은 4개의 뚜렷한 점에서 곡선, 지표면 또는 기타 세트를 교차하는 선입니다.이는 두 점에서 곡선 또는 표면을 교차하는 선인 Secant 선과 [2]세 점에서 곡선 또는 표면을 교차하는 선인 Trisecant와 유사합니다.
4상자는 일반 곡선을 가진 선에서 가능한 가장 많은 교차점을 가지고 있기 때문에 분할자와 3상자에 비해 공간 곡선과 특히 관련이 있다.평면에서는 일반 곡선이 선에 의해 임의로 여러 번 교차할 수 있다.예를 들어 사인 곡선의 작은 일반 섭동은 수평축에 의해 무한히 교차된다.반대로 임의의 공간 곡선이 작은 거리에 의해 교란되어 범용화되면 교란된 곡선의 5개 이상의 지점을 통과하는 선은 없습니다.그럼에도 불구하고, 원래 공간 곡선의 모든 4상자는 그 [3]섭동 부근에 존재할 것이다.
이 현상에 대한 한 가지 설명은 시각적인 것이다.멀리서부터 공간 곡선을 보면, 그러한 시점의 공간은 각 방향에 대응하는 1개의 점이 있는 2차원 구체로 묘사될 수 있다.곡선의 가닥 쌍은 이러한 모든 관점 또는 2차원 부분 집합에서 교차하는 것처럼 보일 수 있습니다.시점이 트리시칸트에 있을 때 3개의 스트랜드가 3중 교차를 형성하고, 4개의 스트랜드가 4중 교차를 형성합니다.한 쌍의 가닥이 다른 가닥에 교차하는 각각의 제약조건은 자유도를 1개(일반적인 곡선의 경우) 감소시키기 때문에, 3각형의 관점은 구의 1차원(연속적으로 무한) 서브셋을 형성하고, 4각형의 관점은 0차원(분리된) 서브셋을 형성한다.C. T. C. Wall은 일반 공간 곡선이 선에 의해 최대 4번 교차된다는 사실은 "가장 단순한 종류의 이론들 중 하나"라고 쓰고 있는데,[3] 이는 고차원 횡단에서의 유사한 이론의 모델 사례이다.
또한 일반적인 공간 곡선의 경우, 4상자는 발생 시 연속된 [4]선군을 형성하는 삼상체와 대조적으로 분리된 선 세트를 형성한다.곡선의 특성에 따라 사층점이 없거나, 수가 많거나, 무한히 많을 수 있습니다.이러한 고려사항들은 사층체의 존재 조건을 결정하거나 [5][6]매듭 곡선, [7]대수 곡선 또는 [8]선의 배열과 같은 다양한 특수한 경우에서 사층체의 수에 대한 경계를 찾는 것을 관심 있게 만든다.
곡선의 특수 클래스용
노트 및 링크
3차원 유클리드 공간에서는 모든 사소한 길들이기 매듭이나 연결은 4차 상승점을 가진다.원래 Erika Pannwitz에 [5]의해 매듭진 다각형과 매끄러운 매듭의 경우에 확립된 이 결과는 적절한 일반적인 위치의 매듭과 0이 아닌 연결 [6]번호와의 연결, 그리고 나중에 모든 사소한 길들여진 매듭과 [9]연결로 확장되었다.
판비츠는 매듭을 경계로 하는 국소적으로 평평한 원반의 경우, 원반의 특이점 수를 사용하여 구별되는 4상계의 수에 대한 하한을 구성할 수 있다는 것을 더욱 강하게 증명했다.이러한 원반은 적어도 하나의 [5][10]특이점을 가지고 있어야 한다는 사실에서 적어도 하나의 4상자의 존재가 뒤따른다.Morton & Mond(1982)는 특정 매듭의 구별되는 4상자의 수가 항상 n 1)/({n(라고 추측했다.서 n n은 [6][10]매듭의 교차 번호이다.이 추측에 대한 반례가 [10]그 이후로 발견되었다.
Two-component 링크가quadrisecant에 지점이 두 components,[6]과 심상치 않은 노트 사이 교류에 나타나는 quadrisecants 네개의 포인트, 주기적으로 결혼에 대한 bcd{abcd\displaystyle}로 주문했다 quadrisecants, 순서대로 quadrisecan을 따라 cbd{\displaystyle acbd} 보이고 있다.t.[11]이러한 교대 4상자의 존재는 중요하지 않은 [11]매듭의 총 곡률에 대한 하한인 Farry-Milnor 정리를 도출하는 데 사용될 수 있다.4중 상승제는 [12]또한 매듭의 로프 길이에 대한 하한을 찾기 위해 사용되어 왔다.
G. T. Jin과 H. S. Kim은 매듭이 있는 에 4상자가 완전히 많을 때 와 4상자가하는 지점에서 K디스플레이 스타일 의 정점과 동등한 매듭을K(K)에 근접시킬 수 있다고 했다. K 그러나 그들의 추측은 틀렸다. 사실 모든 매듭 유형에 대해, 이 구조가 자기 교차 다각형으로 이어진다는 깨달음과 이 구조가 다른 유형의 [13]매듭을 만들어내는 또 다른 깨달음이 있다.
모든 야생 매듭이 무한히 많은 [9]사층부를 가지고 있다고 추측되어 왔다.
대수 곡선
Arthur Cayley는 3차원 복소 사영 공간에서의 대수 곡선의 4상자 수에 대한 공식을 정도와 [7]속 함수로 도출했습니다.및 d의 곡선의 경우, 4상자의 수는[14] 다음과 같습니다.
스큐 라인
3차원 유클리드 공간에서, 일반적인 위치에 있는 네 개의 스큐 선의 모든 집합은 두 개의 4등분(이 문맥에서는 횡단이라고 불리기도 함)을 갖거나 아예 가지지 않는다.4개의 선 중 3개가 쌍곡면, 즉 2개의 선 세트 중 하나가 주어진 3개의 선을 포함하고 다른 1개의 선으로 구성된 이중으로 된 표면을 결정한다.만약 주어진 선들 중 네 번째가 이 표면을 관통한다면, 쌍곡선은 2차 방정식에 의해 정의되기 때문에 두 개의 교차점을 가진다.이 두 점을 통해 피지배 표면의 두 개의 삼등분자가 주어진 네 개의 선의 두 개의 4등분을 형성한다.한편, 네 번째 선이 쌍곡선에서 분리되면 [17]4등성이는 존재하지 않습니다.실제 좌표가 아닌 복잡한 숫자 좌표가 있는 공간에서는 4개의 스큐 라인에 항상 정확히 2개의 [8]사분면이 있습니다.
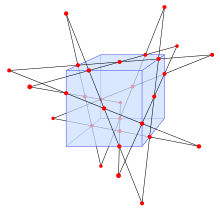
라인 세트의 4상자는 30개의 교차점에서 서로 교차하는 12개의 라인 구성인 슐레플리 더블 6의 건설에 중요한 역할을 한다.의 1, 2, 3, ,의3차원 공간에 5개의 b6displaystyle6가 모두 공통 b6(\{6})과 교차하지만, 그 이외의 에는의 4배수 각각이 됩니다.에는 두 번째 쿼드라이징 가 있으며, 이와 같이 형성된5개의 })는 모두 6과 교차합니다.이 12개의 라인과 30개의 b 스타일 가 더블 [18][19]6을 형성합니다.
주어진 수의 쌍방향 교차로를 갖는n개 \\n개의 선의 배열은 n개 n의 교차로 수로 결정되는 대수 곡선과 그 교차로 수에서 결정되는 속과 그 4층 계수에 사용되는 케일리의 전술한 공식으로 해석될 수 있다.이 공식과 같은 결과는 선의 4배수를 교차점별로 분류하고, 각 유형의 4배수에 대한 4배수를 계산하고,[8] 주어진 집합의 모든 4배수에 대한 합계를 구함으로써 얻을 수 있다.
레퍼런스
- ^ Jin, Gyo Taek (December 2017), "Polygonal approximation of unknots by quadrisecants", in Reiter, Philipp; Blatt, Simon; Schikorra, Armin (eds.), New Directions in Geometric and Applied Knot Theory, De Gruyter Open, pp. 159–175, doi:10.1515/9783110571493-008
- ^ Eisenbud, David; Harris, Joe (2016), 3264 and All That: A second course in algebraic geometry, Cambridge, UK: Cambridge University Press, p. 377, doi:10.1017/CBO9781139062046, ISBN 978-1-107-60272-4, MR 3617981
- ^ a b Wall, C. T. C. (1977), "Geometric properties of generic differentiable manifolds", in Palis, Jacob; do Carmo, Manfredo (eds.), Geometry and Topology: Proceedings of the Latin American School of Mathematics (ELAM III) held at the Instituto de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, July 1976, Lecture Notes in Mathematics, vol. 597, pp. 707–774, doi:10.1007/BFb0085382, MR 0494233
- ^ Denne, Elizabeth (2018), "Quadrisecants and essential secants of knots", in Blatt, Simon; Reiter, Philipp; Schikorra, Armin (eds.), New directions in geometric and applied knot theory, Partial Differential Equations and Measure Theory, De Gruyter, Berlin, pp. 138–158, doi:10.1515/9783110571493-006, MR 3915943, S2CID 128222971
- ^ a b c Pannwitz, Erika (1933), "Eine elementargeometrische Eigenschaft von Verschlingungen und Knoten", Mathematische Annalen, 108 (1): 629–672, doi:10.1007/BF01452857, S2CID 123026724
- ^ a b c d Morton, Hugh R.; Mond, David M. Q. (1982), "Closed curves with no quadrisecants", Topology, 21 (3): 235–243, doi:10.1016/0040-9383(82)90007-6, MR 0649756
- ^ a b Cayley, Arthur (1863), Philosophical Transactions of the Royal Society of London, vol. 153, The Royal Society, pp. 453–483, JSTOR 108806
- ^ a b c Wong, B. C. (1934), "Enumerative properties of -space curves", Bulletin of the American Mathematical Society, 40 (4): 291–296, doi:10.1090/S0002-9904-1934-05854-3, MR 1562839
- ^ a b Kuperberg, Greg (1994), "Quadrisecants of knots and links", Journal of Knot Theory and Its Ramifications, 3: 41–50, arXiv:math/9712205, doi:10.1142/S021821659400006X, MR 1265452, S2CID 6103528
- ^ a b c Jin, Gyo Taek (2005), "Quadrisecants of knots with small crossing number", Physical and numerical models in knot theory (PDF), Ser. Knots Everything, vol. 36, Singapore: World Scientific Publishing, pp. 507–523, doi:10.1142/9789812703460_0025, MR 2197955
- ^ a b Denne, Elizabeth Jane (2004), Alternating quadrisecants of knots, Ph.D. thesis, University of Illinois at Urbana-Champaign, arXiv:math/0510561, Bibcode:2005math.....10561D
- ^ Denne, Elizabeth; Diao, Yuanan; Sullivan, John M. (2006), "Quadrisecants give new lower bounds for the ropelength of a knot", Geometry & Topology, 10: 1–26, arXiv:math/0408026, doi:10.2140/gt.2006.10.1, MR 2207788, S2CID 5770206
- ^ Bai, Sheng; Wang, Chao; Wang, Jiajun (2018), "Counterexamples to the quadrisecant approximation conjecture", Journal of Knot Theory and Its Ramifications, 27 (2), 1850022, arXiv:1605.00538, doi:10.1142/S0218216518500220, MR 3770471, S2CID 119601013
- ^ Griffiths, Phillip; Harris, Joseph (2011), Principles of Algebraic Geometry, Wiley Classics Library, vol. 52, John Wiley & Sons, p. 296, ISBN 9781118030776
- ^ Welchman, W. G. (April 1932), "Note on the trisecants and quadrisecants of a space curve", Mathematical Proceedings of the Cambridge Philosophical Society, 28 (2): 206–208, doi:10.1017/s0305004100010872, S2CID 120725025
- ^ Maxwell, Edwin A. (July 1935), "Note on the formula for the number of quadrisecants of a curve in space of three dimensions", Mathematical Proceedings of the Cambridge Philosophical Society, 31 (3): 324–326, doi:10.1017/s0305004100013086, S2CID 122279811
- ^ Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, p. 164, ISBN 978-0-8284-1087-8
- ^ Schläfli, Ludwig (1858), Cayley, Arthur (ed.), "An attempt to determine the twenty-seven lines upon a surface of the third order, and to derive such surfaces in species, in reference to the reality of the lines upon the surface", Quarterly Journal of Pure and Applied Mathematics, 2: 55–65, 110–120
- ^ ; Coxeter는 Schléfli의 구성을 반복하고, 그 정확성의 단순화된 증명에 대한 몇 가지 참조를 제공한다Coxeter, H. S. M. (2006), "An absolute property of four mutually tangent circles", Non-Euclidean geometries, Math. Appl. (N. Y.), vol. 581, New York: Springer, pp. 109–114, doi:10.1007/0-387-29555-0_5, MR 2191243.



 4상자가 완전히 많을 때
4상자가 완전히 많을 때 
 곡선의 경우, 4상자의 수는
곡선의 경우, 4상자의 수는





 더블
더블 


