priority 큐

컴퓨터 과학에서 priority 큐는 각 요소가 추가로 관련된 priority를 갖는 일반 큐 또는 스택 데이터 구조와 유사한 추상 데이터 유형입니다.priority 큐에서는 priority가 높은 요소가 priority가 낮은 요소보다 먼저 처리된다.구현에 따라서는 2개의 요소가 같은 우선순위를 가지면 큐잉된 순서에 따라 처리됩니다.다른 구현에서는 같은 우선순위를 가진 요소의 순서가 정의되지 않은 채로 있습니다.

코더는 종종 힙을 포함한 priority 큐를 구현하지만 개념적으로는 힙과는 다릅니다.priority 큐는 목록 또는 맵과 같은 개념입니다.목록을 링크된 목록 또는 배열로 구현할 수 있는 것처럼 priority 큐는 힙 또는 정렬되지 않은 배열과 같은 다양한 방법으로 구현할 수 있습니다.

운용

priority 큐는 적어도 다음 작업을 지원해야 합니다.

is_empty: 큐에 요소가 없는지 확인합니다.
insert_with_priority: 연관된 우선순위를 가진 요소를 큐에 추가합니다.
pull_highest_priority_priority: 가장 높은 priority를 가진 요소를 큐에서 삭제하고 반환합니다.
이는 "POP_element(Off)", "get_maximum_element" 또는 "get_front(most)_element"라고도 합니다.

일부 표기법에서는 값이 작을수록 우선순위가 높은 것으로 간주하여 우선순위의 순서를 반대로 하고 있습니다.따라서 이것은 "get_minimum_element"라고도 하며 문헌에서는 "get-min"이라고도 합니다.

대신 "pek_at_highest_priority_element" 및 "delete_element" 함수로 지정할 수 있습니다.이 함수를 조합하여 "pull_highest_priority_element"를 생성할 수 있습니다.

또한 peek(이 컨텍스트에서는 find-max 또는 find-min이라고 불립니다)는 가장 높은 priority 요소를 반환하지만 큐를 변경하지 않고 매우 빈번하게 구현되며 거의 항상 O(1) 시간에 실행됩니다.이 조작과 그 O(1) 퍼포먼스는 priority 큐의 많은 어플리케이션에서 중요합니다.

보다 고도의 실장에서는 pull_lowest_priority_element, 가장 높은 priority 또는 가장 낮은 priority 요소의 검사, 큐의 클리어, 큐의 서브셋의 클리어, 배치 삽입의 실행, 여러 큐의 Marge, 임의의 요소의 priority의 증가 등 보다 복잡한 조작이 지원됩니다.

스택과 큐는 priority 큐와는 다릅니다.priority 큐에서는 삽입되는 값에 따라 순서가 달라집니다.스택 또는 큐에서는 값이 삽입되는 순서에 따라 순서가 달라집니다.동작 서브타이핑에서는 큐는 priority 큐의 서브타입이 아니며 priority 큐는 큐의 서브타입이 아닙니다.어느 한쪽을 다른 한쪽을 대체할 수 없으며 상속 계층에서 한쪽이 다른 한쪽의 하위 유형이어서는 안 됩니다.

실행

간단한 구현

priority 큐를 구현하기 위한 단순하고 비효율적인 방법은 다양합니다.이들은 priority 큐가 무엇인지 이해하는 데 도움이 되는 유사점을 제공합니다.

예를 들어 모든 요소를 정렬되지 않은 목록(O(1) 삽입 시간)에 유지할 수 있습니다.priority가 가장 높은 요소가 요구될 때마다 모든 요소를 검색하여 priority가 가장 높은 요소를 찾습니다.( O ( n )풀타임,

insert(노드) {list.syslog(노드)}

pull() { highest = list.get_first_forach() foreach 노드(if highest.priority < node . priority { highest = node }} list . remove ( highest ) return highest }

다른 경우에는 모든 요소를 우선순위 정렬 목록(O(n) 삽입 정렬 시간)에 유지할 수 있으며, 우선순위가 가장 높은 요소가 요청될 때마다 목록의 첫 번째 요소를 반환할 수 있습니다. (O(1) 풀 시간)

insert(node) { if node . priority < element . priority { list . insert _ at _ index ( node , index ) break } }목록의 foreach ( 인덱스, 요소)가 끊어짐

pull() {highest = list.get_at_index(list.length-1) list.remove(highest) return highest }

통상의 실장

퍼포먼스를 향상시키기 위해 priority 큐는 일반적으로 히프를 기반으로 하며 삽입 및 삭제 시 O(log n) 퍼포먼스를 제공하고 n개의 요소 집합에서 처음에 히프를 구축하기 위해 O(n)를 제공합니다.페어링 힙 또는 피보나치 힙과 같은 기본 힙 데이터 구조의 변형은 일부 작업에 ^[1]더 나은 경계를 제공할 수 있습니다.

또는 자기밸런싱 바이너리 검색 트리를 사용하는 경우 기존 요소 시퀀스에서 트리를 작성하는 데 O(n log n) 시간이 걸리지만 삽입 및 삭제에는 O(log n) 시간이 걸립니다.이것은 서드파티 또는 표준 라이브러리 등 이미 이러한 데이터 구조에 액세스할 수 있는 일반적인 방법입니다.공간 복잡성의 관점에서 링크된 목록과 함께 자체 밸런싱 바이너리 검색 트리를 사용하면 다른 노드에 대한 추가 참조를 저장해야 하므로 더 많은 스토리지가 필요합니다.

계산 복잡성의 관점에서 priority 큐는 정렬 알고리즘과 일치합니다.다음 섹션에서는 priority 큐와 정렬 알고리즘의 동등성에 대해 효율적인 정렬 알고리즘을 통해 효율적인 priority 큐를 생성하는 방법에 대해 설명합니다.

전문 무더기

특정 유형의 키(특히 정수 키)에 대해 추가 작업을 제공하거나 힙 기반 구현을 능가하는 몇 가지 특수한 힙 데이터 구조가 있습니다.사용 가능한 키 집합이 {1, 2, ..., C}이라고 가정합니다.

insert, find-min 및 extract-min만 필요한 경우 정수 priority의 경우 버킷큐를 C 링크 리스트의 $배열$ 과 $포인터$ 톱( $처음$ 에는 C)으로 구성할 수 있습니다.k $키$ 를 가진 아이템을 삽입하면 아이템이 $k$ 'th에 추가되고 top ← $min(top,$ $k)$ 이 모두 일정한 시간에 $업데이트$ 됩니다.extract-min은 목록에서 1개의 항목을 삭제하고 $인덱스$ 상단과 함께 반환한 후 다시 빈 목록이 아닌 목록을 가리킬 때까지 필요에 따라 맨 위로 $증가$ 합니다. 최악의 경우 O $(C)$ 시간이 $걸립니다$ .이러한 큐는 그래프의 ^[2]^{: 374}정점을 정도에 따라 정렬하는 데 유용합니다.
van Emde Boas 트리는 O(log log C) 시간에 최소, 최대, 삽입, 삭제, 검색, 추출, 최대, 추출-최소, 추출-최소, 이전 및 후속 작업을 지원하지만 약 O^m/2(2)의 작은 큐에 대해 공간 비용이 발생합니다.여기서 m은 priority ^[3]값의 비트 수입니다.해시를 사용하면 공간을 크게 줄일 수 있습니다.
Fredman과 Willard에 의한 Fusion 트리는 O(1) 시간 내에 최소 연산을 구현하고 $O(\log n/\log \log C)$ O $(log$ / $log$ C $) 시간$ 내에 삽입 및 추출을 수행합니다.단, 저자에 의해 다음과 같이 기술되어 있습니다. "우리의 알고리즘은 이론적인 관심만을 가지고 있습니다.실행 시간과 관련된 끊임없는 요소 때문에 ^[4]실용성이 떨어집니다."

모든 "extract-min" 조작에 대해 많은 "peak" 조작을 수행하는 애플리케이션의 경우 삽입 및 삭제 후 우선순위가 가장 높은 요소를 캐시함으로써 모든 트리 및 힙 구현에서 Peek 작업의 복잡도를 O(1)로 줄일 수 있습니다.삽입의 경우 새로 삽입된 요소는 이전에 캐시된 최소 요소와만 비교되기 때문에 최대 고정 비용이 추가됩니다.삭제의 경우 최대 "피크" 비용이 추가됩니다.이는 일반적으로 삭제 비용보다 저렴하기 때문에 전체적인 시간 복잡성은 크게 영향을 받지 않습니다.

모노톤 priority 큐는 이전에 추출한 항목보다 priority가 낮은 항목(min-heap의 경우)이 삽입되지 않은 경우에 최적화된 전용 큐입니다.이 제한은 priority 큐의 몇 가지 실제 적용에 의해 충족됩니다.

실행 시간 요약

다음은 다양한 힙 데이터 구조의 시간^[5] 복잡성입니다.함수명은 min-heap을 전제로 합니다."O(f)" 및 "δ(f)"의 의미는 빅 O 표기법을 참조하십시오.

작동	find-min	삭제 최소값	삽입하다	감소 키	혼재
바이너리^[5]	θ(1)	δ(로그 n)	O(log n)	O(log n)	θ(n)
좌파	θ(1)	δ(로그 n)	δ(로그 n)	O(log n)	δ(로그 n)
이항^[5]^[6]	θ(1)	δ(로그 n)	θ(1)^[a]	δ(로그 n)	O(log n)^[b]
피보나치^[5]^[7]	θ(1)	O(log n)^[a]	θ(1)	θ(1)^[a]	θ(1)
페어링^[8]	θ(1)	O(log n)^[a]	θ(1)	o(로그 n)^[a]^[c]	θ(1)
브로달^[11]^[d]	θ(1)	O(log n)	θ(1)	θ(1)	θ(1)
랭크 페어링^[13]	θ(1)	O(log n)^[a]	θ(1)	θ(1)^[a]	θ(1)
엄밀한 피보나치^[14]	θ(1)	O(log n)	θ(1)	θ(1)	θ(1)
2 ~ 3 히프^[15]	O(log n)	O(log n)^[a]	O(log n)^[a]	θ(1)	?

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ 상각시간
^ n은 큰 힙의 크기입니다.
^ 하한 $\Omega (\log \log n),$ ( $\Omega (\log \log n),$ log $\Omega (\log \log n),$ n $\Omega (\log \log n),$ ) $\Omega (\log \log n),$ , {\ $displaystyle \Omega$ ( \ $log \log$ n ) $\Omega (\log \log n),$ $O(2^{2{\sqrt {\log \log n}}}).$ O의 $\Omega (\log \log n),$ ^[9] $O(2^{2{\sqrt {\log \log n}}}).$ ( $O(2^{2{\sqrt {\log \log n}}}).$ $O(2^{2{\sqrt {\log \log n}}}).$ $O(2^{2{\sqrt {\log \log n}}}).$ log $O(2^{2{\sqrt {\log \log n}}}).$ n ) $。{$ $display style$ O ( $2$ ^ { $2$ \ $sq$ \ $log$ \ $log n$ } } 。 $}$ ^[10]
^ Brodal과 Okasaki는 나중에 지원되지 않는 decrement-key를 제외하고 동일한 경계를 가진 영속적인 변종을 기술합니다.n개의 요소가 있는 힙은 O(n)^[12]에서 상향식으로 구성할 수 있습니다.

priority 큐와 정렬 알고리즘의 동등성

priority 큐를 사용하여 정렬

priority 큐의 의미에서는 당연히 정렬 방법을 제안합니다.즉, 정렬할 모든 요소를 priority 큐에 삽입하고 순차적으로 삭제합니다.이러한 요소는 정렬된 순서로 표시됩니다.이는 priority 큐에 의해 제공되는 추상화 레이어가 삭제되면 실제로 여러 정렬 알고리즘에 의해 사용되는 절차입니다.이 정렬 방법은 다음 정렬 알고리즘과 동일합니다.

이름.	priority 큐의 실장	최량	평균	최악의
힙소트	히프	$n\log(n)$	$n\log(n)$	$n\log(n)$
스무스소트	레오나르도 히프	$n$	$n\log(n)$	$n\log(n)$
선택 정렬	정렬되지 않은 어레이	$n^{2}$	$n^{2}$	$n^{2}$
삽입 정렬	순서부여된 어레이	$n$	$n^{2}$	$n^{2}$
트리 정렬	자가 밸런싱 바이너리 검색 트리	$n\log(n)$	$n\log(n)$	$n\log(n)$

정렬 알고리즘을 사용하여 우선순위 대기열 만들기

정렬 알고리즘을 사용하여 priority 큐를 구현할 수도 있습니다.특히 Thorup은 다음과 같이 말합니다.^[16]

priority 큐에서 정렬까지의 일반적인 결정론적 선형 공간 축소를 제시하며, 이는 키당 최대 n개의 키를 정렬할 수 있는 경우 삭제 및 삽입을 지원하는 priority 큐가 O(S(n) 시간에, find-min을 일정 시간에 지원하는 priority 큐가 있음을 의미합니다.

즉, 키당 O(S) 시간으로 정렬할 수 있는 정렬 알고리즘이 있는 경우, 여기서 S는 n과 워드 크기의 ^[17]함수 중 하나이며, priority가 가장 높은 요소를 O(1) 시간으로, 새로운 요소를 삽입(및 삭제)하는 priority 큐를 작성하기 위해 주어진 절차를 사용할 수 있습니다.예를 들어 O(n log n) 정렬 알고리즘이 있는 경우 O(1) 풀링 및 O(n log n) 삽입으로 priority 큐를 작성할 수 있습니다.

라이브러리

priority 큐는 종종 "컨테이너 데이터 구조"로 간주됩니다.

Standard Template Library(STL; 표준 템플릿 라이브러리) 및 C++ 1998 표준에서는 STL 컨테이너 어댑터 클래스 템플릿 중 하나로 std::priority_queue를 지정합니다.다만, 같은 priority를 가지는 2개의 요소의 처리 방법에 대해서는 규정되어 있지 않습니다.또, 일반적인 실장에서는, 큐내의 순서에 따라서 그것들을 반환하지 않습니다.max-priority-queue를 구현하고 3개의 파라미터가 있습니다.이 파라미터는 함수 오브젝트 등의 정렬을 위한 비교 오브젝트(기본값은 less<)입니다.T > 지정되지 않은 경우 데이터 구조를 저장하기 위한 기본 컨테이너(기본값은 std::vector<)T>) 및 시퀀스의 시작과 끝까지의 2개의 반복기.실제 STL 컨테이너와 달리 요소의 반복을 허용하지 않습니다(추상 데이터 유형 정의를 엄격하게 준수합니다).STL에는 바이너리 max-heap으로서 다른 랜덤액세스 컨테이너를 조작하는 유틸리티 기능도 있습니다.Boost 라이브러리는 라이브러리 힙에도 구현되어 있습니다.

Python의 heapq 모듈은 목록 맨 위에 바이너리 min-heap을 구현합니다.

Java 라이브러리에는PriorityQueuemin-priority-priority-priority-priority를 구현합니다

.NET 라이브러리에 우선순위가 있습니다 .큐 클래스: 어레이 백업, 4차 미니히프를 구현합니다.

Scala 라이브러리에 우선 순위가 포함되어 있습니다.max-priority-queue를 구현하는 큐클래스

Go의 라이브러리에는 호환되는 데이터 구조 위에 min-heap을 구현하는 컨테이너/히프 모듈이 포함되어 있습니다.

표준 PHP 라이브러리 확장에 SplPriority 클래스가 포함되어 있습니다.큐잉

Apple의 Core Foundation 프레임워크는 Min-Heap을 구현하는 CFBinaryHeap 구조를 포함하고 있습니다.

적용들

대역폭 관리

priority 큐잉은 네트워크라우터로부터의 전송로 대역폭 등 한정된 자원을 관리하기 위해 사용할 수 있습니다.대역폭 부족으로 인해 발신 트래픽큐잉이 발생했을 경우 다른 모든 큐를 정지하고 도착 시 가장 높은 priority 큐에서 트래픽을 전송할 수 있습니다.이것에 의해, 우선 순위가 매겨진 트래픽(실시간 트래픽, 예를 들면 VoIP 접속의 RTP 스트림 등)이, 큐가 최대 캐퍼시티에 도달해, 지연이 최소한으로, 거부될 가능성이 최소한으로 억제됩니다.가장 높은 priority 큐가 비어 있는 경우 다른 모든 트래픽을 처리할 수 있습니다.사용되는 또 하나의 접근방식은 priority가 높은 큐에서 불균형적으로 많은 트래픽을 전송하는 것입니다.

또한 Local Area Network의 많은 최신 프로토콜에는 미디어 액세스 제어(MAC) 서브레이어에 priority 큐의 개념이 포함되어 있어 우선순위가 높은 애플리케이션(VoIP 또는 IPTV 등)이 베스트 에포트형 서비스로 서비스할 수 있는 다른 애플리케이션보다 지연 시간이 단축됩니다.예를 들어 IEEE 802.11e(서비스 품질을 제공하는 IEEE 802.11의 개정판) 및 ITU-T G.hn(기존 홈 배선(전원선, 전화선, 동축 케이블)을 사용한 고속 로컬에리어 네트워크의 표준판) 등이 있습니다.

보통 priority가 높은 패킷이 다른 모든 트래픽을 차단하지 않도록 하기 위해 priority가 가장 높은 큐에서 트래픽이 취할 수 있는 대역폭을 제한하도록 제한(폴리서)이 설정됩니다.Cisco Call Manager 등의 고도의 제어 인스턴스가 프로그램된 대역폭 제한을 초과하는 콜을 금지하도록 프로그래밍할 수 있기 때문에 보통 이 제한에는 도달하지 않습니다.

이산 이벤트 시뮬레이션

priority 큐의 또 다른 용도는 개별 이벤트 시뮬레이션에서 이벤트를 관리하는 것입니다.이벤트가 큐에 추가되고 시뮬레이션 시간이 우선순위로 사용됩니다.시뮬레이션의 실행은 큐의 상단을 반복하여 당겨서 이벤트를 실행함으로써 진행됩니다.

다음 항목도 참조하십시오.스케줄링(컴퓨팅), 큐잉 이론

다이크스트라 알고리즘

그래프가 인접 리스트 또는 매트릭스 형태로 저장되면 프라이어리티 큐를 사용하여 Dijkstra 알고리즘을 구현할 때 최소한의 효율로 추출할 수 있습니다.단, priority 큐에서 특정 정점의 우선순위를 효율적으로 변경할 수도 있습니다.

그래프가 노드 객체로 저장되고 priority-node 쌍이 힙에 삽입될 경우 방문한 노드를 추적하는 경우 특정 정점의 priority를 변경할 필요가 없습니다.노드가 방문되면 다시 힙으로 올라오면(이전에는 노드에 더 낮은 priority 번호가 관련지어져 있던 경우), 해당 노드는 팝오프되고 무시됩니다.

허프만 부호화

허프만 부호화에서는 두 개의 저주파수 트리를 반복적으로 취득해야 합니다.priority 큐는 이를 위한 방법 중 하나입니다.

베스트 퍼스트 검색 알고리즘

A * 검색 알고리즘과 같이 최선의 우선 검색 알고리즘은 가중 그래프의 두 꼭지점 또는 노드 사이의 최단 경로를 찾아 가장 유망한 경로를 먼저 시도합니다.priority 큐(프린지라고도 함)는 미개척 루트를 추적하기 위해 사용됩니다.패스 길이의 합계 추정치(A*의 경우 하한)가 가장 작은 큐가 가장 우선됩니다.메모리 제한으로 인해 베스트 퍼스트 검색이 실용적이지 않은 경우 대신 SMA* 알고리즘과 같은 변종을 사용하여 우선 순위가 낮은 항목을 삭제할 수 있습니다.

ROAM 삼각 측량 알고리즘

ROAM(Real-time Optimizing Mesh) 알고리즘은 지형의 동적으로 변화하는 삼각 측량을 계산합니다.더 자세한 정보가 필요한 곳에 삼각형을 분할하고 덜 자세한 곳에 병합하는 방식으로 작동합니다.알고리즘은 지형의 각 삼각형에 우선순위를 할당합니다. 일반적으로 해당 삼각형이 분할될 경우 오차 감소와 관련이 있습니다.알고리즘에서는 분할 가능한 삼각형용과 병합 가능한 삼각형용 두 가지 우선순위 큐를 사용합니다.각 단계에서 priority가 가장 높은 스플릿큐의 삼각형이 분할되거나 priority가 가장 낮은 머지큐의 삼각형이 네이버와 Marge됩니다.

최소 스패닝 트리를 위한 Prim 알고리즘

Prim 알고리즘에서 min 힙 priority 큐를 사용하여 연결된 그래프와 무방향 그래프의 최소 스패닝 트리를 찾음으로써 좋은 실행 시간을 얻을 수 있습니다.이 최소 힙priority 큐는 insert, minimum, extract-min, decrement-key ^[18]등의 작업을 지원하는 최소 힙 데이터 구조를 사용합니다.이 구현에서는 모서리의 무게를 사용하여 정점의 우선순위를 결정합니다.가중치를 낮추고 우선순위를 높이며 가중치를 높이면 우선순위를 낮춥니다.^[19]

병렬 priority 큐

병렬화를 사용하여 priority 큐의 속도를 높일 수 있지만 priority 큐인터페이스를 변경해야 합니다.The reason for such changes is that a sequential update usually only has ${\textstyle O(1)}$ or ${\textstyle O(\log n)}$ cost, and there is no practical gain to parallelize such an operation.가능한 변경 사항 중 하나는 여러 프로세서가 동일한 priority 큐에 동시에 액세스할 수 있도록 하는 것입니다.두 번째 변경은 하나의 요소가 아니라 k $\textstyle$ k $\$ ${\textstyle k}$ 에서 동작하는 배치 조작을 허용하는 것입니다.예를 들어 extractMin은 우선순위가 가장 높은 첫 ${\textstyle k}$ k개의 \ $textstyle$ k 요소를 ${\textstyle k}$ 삭제합니다.

동시 병렬 액세스

priority 큐에 동시 액세스가 허용되면 여러 프로세스가 해당 priority 큐에서 동시에 작업을 수행할 수 있습니다.하지만, 이것은 두 가지 문제를 제기한다.무엇보다도, 개별 운영의 의미론의 정의는 더 이상 명확하지 않다.예를 들어, 두 프로세스가 가장 높은 우선순위를 가진 요소를 추출하는 경우 동일한 요소를 얻을 것인지 아니면 다른 요소를 얻을 것인지를 결정합니다.이로 인해 priority 큐를 사용하는 프로그램레벨에서의 병렬화가 제한됩니다.또한 여러 프로세스가 동일한 요소에 액세스할 수 있기 때문에 경합이 발생합니다.

노드 3이 삽입되어 노드 2의 포인터를 노드 3으로 설정합니다.그 직후 노드 2를 삭제하고 노드 1의 포인터를 노드 4로 설정한다.이제 노드 3에 도달할 수 없게 되었습니다.

priority 큐에 대한 동시 액세스는 Concurrent Read, Concurrent Write(CRCW; 동시 읽기, 동시 쓰기) PRAM 모델에 구현할 수 있습니다.다음에서는 priority 큐가 건너뛰기 ^[20]^[21]목록으로 구현됩니다.또, 아토믹 동기 프리미티브(CAS)를 사용해 스킵 리스트를 록 프리하게 합니다.건너뛰기 목록의 노드는 고유한 키, 우선순위, 각 레벨의 포인터 배열, 다음 노드에 대한 삭제 마크로 구성됩니다.삭제 마크는 노드가 프로세스에 의해 삭제될 경우 표시됩니다.이를 통해 다른 프로세스가 삭제에 적절하게 반응할 수 있습니다.

삽입(e):우선, 키와 priority를 가지는 새로운 노드가 작성됩니다.또한 노드에는 포인터 배열의 크기를 결정하는 여러 레벨이 할당됩니다.그런 다음 검색을 수행하여 새 노드를 삽입할 올바른 위치를 찾습니다.검색은 첫 번째 노드부터 가장 높은 수준에서 시작됩니다.그런 다음 올바른 위치를 찾을 때까지 가장 낮은 수준으로 건너뜁니다.검색 중에 모든 레벨에서 마지막으로 통과한 노드가 해당 레벨의 새 노드에 대한 상위 노드로 저장됩니다.또한 부모 노드의 포인터가 가리키는 노드는 해당 수준에서 새 노드의 후계 노드로 저장됩니다.이후 새 노드의 모든 레벨에 대해 부모 노드의 포인터가 새 노드로 설정됩니다.마지막으로 새로운 노드의 포인터는 모든 레벨에서 대응하는 후계 노드로 설정됩니다.
extract-min:우선 삭제 마크가 설정되어 있지 않은 노드에 도달할 때까지 건너뛰기 리스트를 통과시킨다.이 삭제 마크는 해당 노드에 대해 true로 설정되어 있습니다.마지막으로 삭제된 노드의 부모 노드의 포인터를 갱신한다.

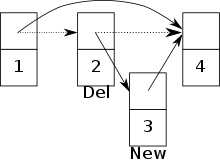
priority 큐에 대한 동시 액세스가 허용되면 두 프로세스 간에 충돌이 발생할 수 있습니다.예를 들어, 한 프로세스가 새 노드를 삽입하려고 하지만 동시에 다른 프로세스가 해당 ^[20]노드의 이전 노드를 삭제하려고 하면 충돌이 발생합니다.새 노드가 건너뛰기 목록에 추가될 위험이 있지만 더 이상 연결할 수 없습니다.(이미지 참조)

K-element 작업

이 설정에서는 priority 큐에서의 조작은 k $\textstyle$ k 요소의 ${\textstyle k}$ ${\textstyle k}$ 로 일반화됩니다.예를 들어 k_extract-min은 priority 큐의 k $\textstyle$ k의 최소 ${\textstyle k}$ ${\textstyle k}$ 를 삭제하고 이를 반환합니다.

공유 메모리 설정에서는 병렬 바이너리 검색 트리 및 조인 기반 트리 알고리즘을 사용하여 병렬 우선 큐를 쉽게 구현할 수 있다.특히 k_extract-min은 O ${\textstyle O(\log n)}$ n $)\textstyle$ O $(\log$ n $)$ 비용을 가지며 ${\textstyle O(\log n)}$ ${\textstyle O(\log n)}$ $(\textstyle$ k $)$ 의 ${\textstyle k}$ 최소 요소를 포함하는 트리를 생성하는 바이너리 검색 트리의 분할에 대응합니다.k_insert는 원래 priority 큐와 삽입 배치를 결합하여 적용할 수 있습니다.배치가 이미 키별로 정렬되어 있는 경우 k_insert의 ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ 은 ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ ( $k$ log ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ ( 1 + ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ k ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ ) { $textstyle O$ ( k \ $log$ ( 1 + { \ $frac$ { $n$ } { k ${\textstyle O(k\log(1+{\frac {n}{k}}))}$ } ) 。그렇지 않으면 먼저 배치를 정렬해야 하므로 비용은 ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ log ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ ( ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ + ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ ) + ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ log ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ k ) $=$ ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ log ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ n ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ ) { $textstyle$ O $(k\log(1+{\frac {n}})+k\log$ k)= $O(k\log$ n ${\textstyle O(k\log(1+{\frac {n}{k}})+k\log k)=O(k\log n)}$ priority 큐의 다른 조작도 마찬가지로 적용할 수 있습니다.예를 들어, k_decrease-key는 처음에 차분을 적용한 후 결합함으로써 실행할 수 있습니다.이것에 의해, 우선 요소가 삭제되고 나서, 갱신된 키에 의해서 다시 삽입됩니다.이러한 모든 연산은 매우 병렬적이며 이론적이고 실제적인 효율성은 관련 ^[22]^[23]연구 논문에서 확인할 수 있습니다.

이 섹션의 나머지 부분에서는 분산 메모리의 큐 기반 알고리즘에 대해 설명합니다.각 프로세서에 독자적인 로컬메모리와 로컬(시퀀셜) priority 큐가 있다고 가정합니다.글로벌(병렬) priority 큐의 요소는 모든 프로세서에 분산되어 있습니다.

k_priority-min은 3개의 프로세서를 갖춘 priority 큐에서 실행됩니다.녹색 요소가 반환되어 priority 큐에서 삭제됩니다.

k_insert 조작은 요소를 로컬큐에 삽입하는 프로세서에 균일하게 랜덤으로 할당합니다.단일 요소는 큐에 삽입할 수 있습니다.이 전략을 사용하면 모든 프로세서의 로컬 최소 요소가 높은 확률로 결합됩니다.따라서 각 프로세서는 글로벌priority 큐의 대표적인 부분을 유지합니다.

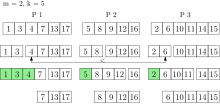
이 속성은 k_extract-min 실행 시 사용됩니다.각 로컬큐의 $최소$ 의 $요소$ 가 ${\textstyle m}$ 삭제되어 결과 세트에 수집되기 때문입니다.결과 세트내의 요소는, 원래의 프로세서에 관련지어져 있습니다.각 로컬 큐에서 삭제되는 $요소$ m(\ $textstyle$ m $)$ 의 ${\textstyle m}$ 수는 k $(\textstyle$ k $)$ 와 ${\textstyle k}$ ${\textstyle p}$ p $(\textstyle$ p ${\textstyle p}$ 에 ${\textstyle k}$ 달라집니다^[24].패럴렐 선택에 의해 결과 세트의 최소 요소 ${\textstyle k}$ k(\ $textstyle$ k $)$ 가 ${\textstyle k}$ 결정됩니다.이러한 요소는 글로벌 ${\textstyle k}$ k개 $요소$ 일 ${\textstyle k}$ $가능성$ 이 높습니다 $.$ ${\textstyle m}$ 않으면 각 로컬 큐에서 m $\textstyle$ m 요소가 ${\textstyle m}$ 다시 삭제되어 결과 세트에 추가됩니다.이 작업은 글로벌 $최소$ 요소 $k개가$ 결과 세트에 포함될 때까지 수행됩니다. ${\textstyle k}$ 이러한 $k개의 요소$ 를 ${\textstyle k}$ 반환할 수 있습니다 $.$ 결과 세트의 다른 모든 요소는 로컬 큐에 다시 삽입됩니다.k_textstyle-min 실행시간은 O ${\textstyle O({\frac {k}{p}}\log(n))}$ ${\textstyle O({\frac {k}{p}}\log(n))}$ log ${\textstyle O({\frac {k}{p}}\log(n))}$ ( ${\textstyle O({\frac {k}{p}}\log(n))}$ n $){\textstyle$ O $({\$ ${\textstyle k=\Omega (p\cdot \log(p))}$ ${k}{p}}\log($ ${\textstyle k=\Omega (p\cdot \log(p))}$ $)})}$ 입니다 ${\textstyle O({\frac {k}{p}}\log(n))}$ ${\textstyle n}$ 서 k $=$ $))\textstyle$ ^[24]n의 priority는 n입니다 ${\textstyle k=\Omega (p\cdot \log(p))}$ .

priority 큐는 k_extract-min 조작 후 결과 세트의 나머지 요소를 직접 로컬큐로 이동하지 않는 것으로 한층 더 개선할 수 있습니다.이렇게 하면 결과 세트와 로컬 큐 사이에서 항상 앞뒤로 이동하는 요소가 저장됩니다.

여러 요소를 한 번에 제거함으로써 상당한 속도 향상에 도달할 수 있습니다.그러나 모든 알고리즘이 이러한 종류의 priority 큐를 사용할 수 있는 것은 아닙니다.예를 들어 Dijkstra의 알고리즘은 여러 노드에서 동시에 작동할 수 없습니다.이 알고리즘은 priority 큐에서 가장 거리가 작은 노드를 가져와 모든 네이버노드에 대해 새로운 거리를 계산합니다. $k개의 노드$ 를 ${\textstyle k}$ ${\textstyle k}$ 할 경우, 한 노드에서 작업하면 $k개의 노드$ 중 다른 노드의 거리가 변경될 수 있습니다.따라서 k-element 연산을 사용하면 Dijkstra 알고리즘의 라벨 설정 속성이 파괴됩니다.

「」를 참조해 주세요.

레퍼런스

^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Chapter 20: Fibonacci Heaps". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 476–497. ISBN 0-262-03293-7. 제3판 518쪽
^ Skiena, Steven (2010). The Algorithm Design Manual (2nd ed.). Springer Science+Business Media. ISBN 978-1-849-96720-4.
^ P. 반 엠데 보아스로그 시간보다 짧은 시간에 포레스트에 순서를 보존합니다.제16회 컴퓨터 사이언스 기초 심포지엄 진행(75-84페이지)IEEE Computer Society, 1975.
^ 마이클 L. 프레드먼과 댄 E.윌러드.퓨전 트리로 묶인 이론적인 정보를 능가한다.컴퓨터 및 시스템 과학 저널, 48(3): 533-551, 1994
^ ^a ^b ^c ^d Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990). Introduction to Algorithms (1st ed.). MIT Press and McGraw-Hill. ISBN 0-262-03141-8.
^ "Binomial Heap Brilliant Math & Science Wiki". brilliant.org. Retrieved 2019-09-30.
^ Fredman, Michael Lawrence; Tarjan, Robert E. (July 1987). "Fibonacci heaps and their uses in improved network optimization algorithms" (PDF). Journal of the Association for Computing Machinery. 34 (3): 596–615. CiteSeerX 10.1.1.309.8927. doi:10.1145/28869.28874.
^ Iacono, John (2000), "Improved upper bounds for pairing heaps", Proc. 7th Scandinavian Workshop on Algorithm Theory (PDF), Lecture Notes in Computer Science, vol. 1851, Springer-Verlag, pp. 63–77, arXiv:1110.4428, CiteSeerX 10.1.1.748.7812, doi:10.1007/3-540-44985-X_5, ISBN 3-540-67690-2
^ Fredman, Michael Lawrence (July 1999). "On the Efficiency of Pairing Heaps and Related Data Structures" (PDF). Journal of the Association for Computing Machinery. 46 (4): 473–501. doi:10.1145/320211.320214.
^ Pettie, Seth (2005). Towards a Final Analysis of Pairing Heaps (PDF). FOCS '05 Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science. pp. 174–183. CiteSeerX 10.1.1.549.471. doi:10.1109/SFCS.2005.75. ISBN 0-7695-2468-0.
^ Brodal, Gerth S. (1996), "Worst-Case Efficient Priority Queues" (PDF), Proc. 7th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 52–58
^ Goodrich, Michael T.; Tamassia, Roberto (2004). "7.3.6. Bottom-Up Heap Construction". Data Structures and Algorithms in Java (3rd ed.). pp. 338–341. ISBN 0-471-46983-1.
^ Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (November 2011). "Rank-pairing heaps" (PDF). SIAM J. Computing. 40 (6): 1463–1485. doi:10.1137/100785351.
^ Brodal, Gerth Stølting; Lagogiannis, George; Tarjan, Robert E. (2012). Strict Fibonacci heaps (PDF). Proceedings of the 44th symposium on Theory of Computing - STOC '12. pp. 1177–1184. CiteSeerX 10.1.1.233.1740. doi:10.1145/2213977.2214082. ISBN 978-1-4503-1245-5.
^ Takaoka, Tadao (1999), Theory of 2–3 Heaps (PDF), p. 12
^ Thorup, Mikkel (2007). "Equivalence between priority queues and sorting". Journal of the ACM. 54 (6): 28. doi:10.1145/1314690.1314692. S2CID 11494634.
^ "Archived copy" (PDF). Archived (PDF) from the original on 2011-07-20. Retrieved 2011-02-10.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)
^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. p. 634. ISBN 0-262-03384-4. "Prim의 알고리즘을 효율적으로 구현하기 위해서는 A의 엣지에 의해 형성된 트리에 추가할 새로운 엣지를 빠르게 선택할 수 있는 방법이 필요합니다.
^ "Prim's Algorithm". Geek for Geeks. Archived from the original on 9 September 2014. Retrieved 12 September 2014.
^ ^a ^b Sundell, Håkan; Tsigas, Philippas (2005). "Fast and lock-free concurrent priority queues for multi-thread systems". Journal of Parallel and Distributed Computing. 65 (5): 609–627. doi:10.1109/IPDPS.2003.1213189. S2CID 20995116.
^ Lindén, Jonsson (2013), "A Skiplist-Based Concurrent Priority Queue with Minimal Memory Contention", Technical Report 2018-003 (in German)
^ Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just Join for Parallel Ordered Sets", Symposium on Parallel Algorithms and Architectures, Proc. of 28th ACM Symp. Parallel Algorithms and Architectures (SPAA 2016), ACM, pp. 253–264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793
^ Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2018), "PAM: parallel augmented maps", Proceedings of the 23rd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, ACM, pp. 290–304
^ ^a ^b Sanders, Peter; Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (2019). Sequential and Parallel Algorithms and Data Structures - The Basic Toolbox. Springer International Publishing. pp. 226–229. doi:10.1007/978-3-030-25209-0. ISBN 978-3-030-25208-3. S2CID 201692657.

추가 정보

Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Section 6.5: Priority queues". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 138–142. ISBN 0-262-03293-7.

외부 링크

C++ 참조:std::priority_queue
리 킬러에 의한 설명
PQlib - C용 오픈소스 Priority Queue 라이브러리
libpqueue는 Apache HTTP Server 프로젝트에서 사용되는 범용 priority 큐(히프) 구현입니다(C).
Stefan Xenos에 의한 기존의 priority 큐 구조 조사
UC 버클리 - 컴퓨터 과학 61B - 강의 24: 우선 큐 (비디오) - 이진 힙을 사용한 우선 큐 소개

[amortized-7] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ 상각시간

[meld-8] 은 큰 힙의 크기입니다.

[pairingdecreasekey-13] 하한 $\Omega (\log \log n),$ ( $\Omega (\log \log n),$ log $\Omega (\log \log n),$ n $\Omega (\log \log n),$ ) $\Omega (\log \log n),$ , {\ $displaystyle \Omega$ ( \ $log \log$ n ) $\Omega (\log \log n),$ $O(2^{2{\sqrt {\log \log n}}}).$ O의 $\Omega (\log \log n),$ ^[9] $O(2^{2{\sqrt {\log \log n}}}).$ ( $O(2^{2{\sqrt {\log \log n}}}).$ $O(2^{2{\sqrt {\log \log n}}}).$ $O(2^{2{\sqrt {\log \log n}}}).$ log $O(2^{2{\sqrt {\log \log n}}}).$ n ) $。{$ $display style$ O ( $2$ ^ { $2$ \ $sq$ \ $log$ \ $log n$ } } 。 $}$ ^[10]

[brodal-16] Brodal과 Okasaki는 나중에 지원되지 않는 decrement-key를 제외하고 동일한 경계를 가진 영속적인 변종을 기술합니다.n개의 요소가 있는 힙은 O(n)^[12]에서 상향식으로 구성할 수 있습니다.

[CLRS_priority_queue_pp476-1] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "Chapter 20: Fibonacci Heaps". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 476–497. ISBN 0-262-03293-7. 제3판 518쪽

[2] Skiena, Steven (2010). The Algorithm Design Manual (2nd ed.). Springer Science+Business Media. ISBN 978-1-849-96720-4.

[3] P. 반 엠데 보아스로그 시간보다 짧은 시간에 포레스트에 순서를 보존합니다.제16회 컴퓨터 사이언스 기초 심포지엄 진행(75-84페이지)IEEE Computer Society, 1975.

[4] 마이클 L. 프레드먼과 댄 E.윌러드.퓨전 트리로 묶인 이론적인 정보를 능가한다.컴퓨터 및 시스템 과학 저널, 48(3): 533-551, 1994

[CLRS-5] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990). Introduction to Algorithms (1st ed.). MIT Press and McGraw-Hill. ISBN 0-262-03141-8.

[6] "Binomial Heap Brilliant Math & Science Wiki". brilliant.org. Retrieved 2019-09-30.

[Fredman_And_Tarjan-9] Fredman, Michael Lawrence; Tarjan, Robert E. (July 1987). "Fibonacci heaps and their uses in improved network optimization algorithms" (PDF). Journal of the Association for Computing Machinery. 34 (3): 596–615. CiteSeerX 10.1.1.309.8927. doi:10.1145/28869.28874.

[Iacono-10] Iacono, John (2000), "Improved upper bounds for pairing heaps", Proc. 7th Scandinavian Workshop on Algorithm Theory (PDF), Lecture Notes in Computer Science, vol. 1851, Springer-Verlag, pp. 63–77, arXiv:1110.4428, CiteSeerX 10.1.1.748.7812, doi:10.1007/3-540-44985-X_5, ISBN 3-540-67690-2

[Fredman1999-11] Fredman, Michael Lawrence (July 1999). "On the Efficiency of Pairing Heaps and Related Data Structures" (PDF). Journal of the Association for Computing Machinery. 46 (4): 473–501. doi:10.1145/320211.320214.

[12] Pettie, Seth (2005). Towards a Final Analysis of Pairing Heaps (PDF). FOCS '05 Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science. pp. 174–183. CiteSeerX 10.1.1.549.471. doi:10.1109/SFCS.2005.75. ISBN 0-7695-2468-0.

[14] Brodal, Gerth S. (1996), "Worst-Case Efficient Priority Queues" (PDF), Proc. 7th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 52–58

[15] Goodrich, Michael T.; Tamassia, Roberto (2004). "7.3.6. Bottom-Up Heap Construction". Data Structures and Algorithms in Java (3rd ed.). pp. 338–341. ISBN 0-471-46983-1.

[17] Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (November 2011). "Rank-pairing heaps" (PDF). SIAM J. Computing. 40 (6): 1463–1485. doi:10.1137/100785351.

[18] Brodal, Gerth Stølting; Lagogiannis, George; Tarjan, Robert E. (2012). Strict Fibonacci heaps (PDF). Proceedings of the 44th symposium on Theory of Computing - STOC '12. pp. 1177–1184. CiteSeerX 10.1.1.233.1740. doi:10.1145/2213977.2214082. ISBN 978-1-4503-1245-5.

[19] Takaoka, Tadao (1999), Theory of 2–3 Heaps (PDF), p. 12

[20] Thorup, Mikkel (2007). "Equivalence between priority queues and sorting". Journal of the ACM. 54 (6): 28. doi:10.1145/1314690.1314692. S2CID 11494634.

[21] "Archived copy" (PDF). Archived (PDF) from the original on 2011-07-20. Retrieved 2011-02-10.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)

[CLR-22] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. p. 634. ISBN 0-262-03384-4. "Prim의 알고리즘을 효율적으로 구현하기 위해서는 A의 엣지에 의해 형성된 트리에 추가할 새로운 엣지를 빠르게 선택할 수 있는 방법이 필요합니다.

[GEEKS-23] "Prim's Algorithm". Geek for Geeks. Archived from the original on 9 September 2014. Retrieved 12 September 2014.

[skiplist-24] Sundell, Håkan; Tsigas, Philippas (2005). "Fast and lock-free concurrent priority queues for multi-thread systems". Journal of Parallel and Distributed Computing. 65 (5): 609–627. doi:10.1109/IPDPS.2003.1213189. S2CID 20995116.

[25] Lindén, Jonsson (2013), "A Skiplist-Based Concurrent Priority Queue with Minimal Memory Contention", Technical Report 2018-003 (in German)

[join-based-26] Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just Join for Parallel Ordered Sets", Symposium on Parallel Algorithms and Architectures, Proc. of 28th ACM Symp. Parallel Algorithms and Architectures (SPAA 2016), ACM, pp. 253–264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793

[pam-27] Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2018), "PAM: parallel augmented maps", Proceedings of the 23rd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, ACM, pp. 290–304

[AlgToolbox-28] Sanders, Peter; Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (2019). Sequential and Parallel Algorithms and Data Structures - The Basic Toolbox. Springer International Publishing. pp. 226–229. doi:10.1007/978-3-030-25209-0. ISBN 978-3-030-25208-3. S2CID 201692657.

[1]

[2]

[3]

[4]

[5]

[6]

[a]

[b]

[7]

[8]

[c]

[11]

[d]

[13]

[14]

[15]

[9]

[10]

[12]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

v t 잘 알려진 데이터 구조
종류들	수집 컨테이너.
추상적인	연관 배열 멀티맵 데이터 구조 검색 목록. 스택 큐 더블 엔드 큐 priority 큐 이중 엔드 priority 큐 세트 멀티셋 디조인트 세트
어레이	비트 배열 순환 버퍼 다이내믹 어레이 해시 테이블 해시 어레이 트리 희박 행렬
링크되어 있다	어소시에이션리스트 링크 리스트 스킵 리스트 언롤링된 링크 리스트 XOR 링크 리스트
나무들	B-트리 이진 검색 트리 AA나무 AVL 트리 붉은색-검은색 셀프밸런싱 트리 스플레이 트리 히프 이진 힙 이항 힙 피보나치 힙 R 트리 R* 트리 R+ 트리 힐베르트 R-트리 트리 해시 트리
그래프	이항 결정도 방향 비순환 그래프 지시 비순환 단어 그래프
데이터 구조 목록

Search

priority 큐

네임스페이스

더

목차

운용

실행

간단한 구현

통상의 실장

전문 무더기

실행 시간 요약

priority 큐와 정렬 알고리즘의 동등성

priority 큐를 사용하여 정렬

정렬 알고리즘을 사용하여 우선순위 대기열 만들기

라이브러리

적용들

대역폭 관리

이산 이벤트 시뮬레이션

다이크스트라 알고리즘

허프만 부호화

베스트 퍼스트 검색 알고리즘

ROAM 삼각 측량 알고리즘

최소 스패닝 트리를 위한 Prim 알고리즘

병렬 priority 큐

동시 병렬 액세스

K-element 작업

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

priority 큐

운용

실행

간단한 구현

통상의 실장

전문 무더기

실행 시간 요약

priority 큐와 정렬 알고리즘의 동등성

priority 큐를 사용하여 정렬

정렬 알고리즘을 사용하여 우선순위 대기열 만들기

라이브러리

적용들

대역폭 관리

이산 이벤트 시뮬레이션

다이크스트라 알고리즘

허프만 부호화

베스트 퍼스트 검색 알고리즘

ROAM 삼각 측량 알고리즘

최소 스패닝 트리를 위한 Prim 알고리즘

병렬 priority 큐

동시 병렬 액세스

K-element 작업

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.