영속적인 데이터 구조
Persistent data structure컴퓨팅에서 영구 데이터 구조 또는 사용 후 삭제되지 않은 데이터 구조는 이전 버전을 수정할 때 항상 보존하는 데이터 구조입니다.이러한 데이터 구조는 실질적으로 불변합니다. 왜냐하면 이러한 운영은 구조를 (가시적으로) 업데이트하지 않고 항상 새로 업데이트된 구조를 생성하기 때문입니다.이 용어는 드리스콜, 사르낙, 슬레이터, 타잔스의 1986년 [1]기사에 소개되었습니다.
모든 버전에 액세스할 수 있지만 최신 버전만 수정할 수 있는 경우 데이터 구조는 부분적으로 유지됩니다.모든 버전에 액세스하고 수정할 수 있는 경우 데이터 구조는 완전히 유지됩니다.이전 두 버전에서 새 버전을 만들 수 있는 meld 또는 merge 작업이 있는 경우 데이터 구조는 병합 영속적이라고 불립니다.지속적이지 않은 구조를 사용 후 [2]삭제라고 합니다.
이러한 유형의 데이터 구조는 논리 [2]및 기능 프로그래밍에서 특히 일반적이며, 이러한 패러다임의 언어들이 가변 데이터의 사용을 금지(또는 완전히 금지)하기 때문입니다.
부분적 지속성과 완전 지속성
부분 지속성 모델에서 프로그래머는 데이터 구조의 이전 버전을 쿼리할 수 있지만 최신 버전만 업데이트할 수 있습니다.이는 데이터 [3]구조의 각 버전 간에 선형 순서가 있음을 의미합니다.완전 영속 모델에서는 모든 버전의 데이터 구조에서 업데이트와 조회가 모두 허용됩니다.경우에 따라서는 로프 데이터 [4]구조에서와 같이 데이터 구조의 이전 버전을 쿼리하거나 업데이트하는 성능 특성이 저하될 수 있습니다.또한 데이터 구조는 완전히 영속적일 뿐만 아니라 동일한 데이터 구조의 두 버전을 결합하여 여전히 완전히 [5]영속적인 새로운 버전을 형성할 수 있는 경우 융합 영속적이라고 할 수 있습니다.
이전 버전을 보존하는 기술
카피 온 라이트
영속적인 데이터 구조를 작성하기 위한 한 가지 방법은 데이터 구조에 데이터를 저장하기 위해 어레이와 같은 플랫폼 제공 에페머럴 데이터 구조를 사용하고 데이터 구조의 업데이트에 대해 Copy-on-Write 시멘틱스를 사용하여 데이터 구조 전체를 복사하는 것입니다.쓰기마다 백업 데이터 구조 전체를 복사해야 하기 때문에 크기가 [citation needed]n인 배열의 m개 수정 시 최악의 경우 O(n·m) 성능 특성이 발생하므로 이는 비효율적인 기술입니다.
지방 노드
팻 노드 방식은 노드의 필드에 대한 모든 변경 내용을 노드의 오래된 값을 지우지 않고 노드 자체에 기록합니다.이를 위해서는 노드가 임의로 "뚱보"가 되도록 허용해야 합니다.즉, 각 fat 노드에는 ephemeral 노드와 동일한 정보 및 포인터 필드가 포함되며 임의의 수의 추가 필드 값을 위한 공간도 포함됩니다.각 추가 필드 값에는 연관된 필드 이름과 지정된 값을 가지도록 이름이 지정된 필드가 변경된 버전을 나타내는 버전 스탬프가 있습니다.또한 각 Fat 노드에는 노드가 작성된 버전을 나타내는 자체 버전 스탬프가 있습니다.노드에 버전 스탬프가 있는 유일한 목적은 각 노드에 버전별로 필드 이름당 값이 1개만 포함되도록 하는 것입니다.구조체를 탐색하기 위해 노드 내의 각 원래 필드 값은 0 버전 스탬프를 가집니다.
지방 노드의 복잡성
팻 노드 방법을 사용하면 모든 수정에 O(1) 공간이 필요합니다. 새 데이터를 저장하기만 하면 됩니다.각 변경은 변경 이력의 마지막에 변경을 저장하는 데 O(1)의 추가 시간이 걸립니다.이는 변경 이력이 확장 가능한 배열에 저장되어 있다고 가정할 때 상각된 기간입니다.액세스 시 구조를 통과할 때 각 노드에서 올바른 버전을 찾아야 합니다.「m」의 변경을 실시하는 경우, 어레이내의 가장 가까운 변경을 검출하는 코스트에 의해, 각 액세스 조작에 O(log m)의 속도가 저하합니다.
패스 복사
경로 복사 방법을 사용하면 변경하려는 노드에 대한 경로에서 모든 노드의 복사가 만들어집니다.이러한 변경은 데이터 구조를 통해 캐스케이드백해야 합니다.오래된 노드를 가리키던 모든 노드를 새 노드를 가리키도록 변경해야 합니다.이러한 변경에 의해 루트노드에 도달할 때까지 캐스케이드 변경 등이 이루어집니다.
경로 복사의 복잡성
m의 수정으로 O(log m)의 추가 조회 시간이 소요됩니다.수정 시간과 공간은 데이터 구조에서 가장 긴 경로의 크기와 에페메랄 데이터 구조에서의 업데이트 비용에 의해 제한된다.부모 포인터가 없는 Balanced Binary Search Tree에서는 수정 시간의 복잡성이 O(log n + update cost)입니다.다만, 링크 리스트에서는, 최악의 경우 변경 시간의 복잡도는 O(n+갱신 코스트)입니다.
조합
Driscell, Sarnak, Sleator, Tarjan은 Fat 노드와 경로 복사 기술을 결합하여 O(1) 액세스 속도 저하와 O(1) 변경 시공간 및 시간 복잡성을 실현하는 방법을 생각해냈습니다[1].
각 노드에는 1개의 수정 상자가 격납되어 있다.이 상자에는 포인터, 노드의 키 또는 기타 노드 고유의 데이터에 대한 수정 및 해당 수정이 적용된 시점의 타임스탬프를 저장할 수 있습니다.처음에는 모든 노드의 수정 상자가 비어 있습니다.
노드에 액세스 할 때마다 변경 상자가 체크되어 그 타임 스탬프가 액세스 시간과 비교됩니다.(접근 시간은 고려 중인 데이터 구조의 버전을 지정합니다).수정 상자가 비어 있거나 접근 시간이 수정 시간 이전일 경우 수정 상자는 무시되고 노드의 일반 부분만 고려됩니다.한편, 액세스 시간이 변경 시간 이후인 경우는, 변경 상자의 값이 사용되고, 노드내의 그 값이 덮어씁니다.
노드를 수정하면 다음과 같이 동작합니다(각 수정이 포인터 또는 유사한 필드에 닿는 것으로 가정합니다).노드의 수정 상자가 비어 있으면 수정으로 채워집니다.그렇지 않으면 수정 상자가 꽉 찼습니다.노드의 복사본이 작성되지만 최신 값만 사용합니다.수정 상자를 사용하지 않고 새 노드에서 직접 수정이 수행됩니다(새 노드의 필드 중 하나가 덮어쓰여지고 수정 상자는 비어 있음).마지막으로 이 변경은 경로 복사와 마찬가지로 노드의 부모에게 캐스케이드됩니다.(이 작업에는 부모의 수정 상자를 채우거나 부모의 복사본을 반복적으로 만드는 작업이 포함될 수 있습니다.노드에 부모(루트)가 없는 경우 새 루트가 정렬된 루트 배열에 추가됩니다.)
이 알고리즘에서는 임의의 시간 t에 대해 최대 1개의 수정 상자가 시간 t의 데이터 구조 내에 존재합니다.따라서 시각 t에서의 수정은 트리를 세 부분으로 분할합니다.하나는 시각 t 이전의 데이터를 포함하고, 다른 하나는 시각 t 이후의 데이터를 포함하고, 다른 하나는 수정의 영향을 받지 않습니다.
조합의 복잡성
수정을 위한 시간과 공간은 상각된 분석이 필요합니다.수정에는 O(1) 상각된 공간과 O(1) 상각된 시간이 소요됩니다.그 이유를 확인하려면 잠재적인 함수 '를 사용합니다.여기서 '(T)'는 T의 완전한 라이브노드의 수입니다.T의 라이브노드는 현재(즉, 마지막 변경 후) 현재 루트에서 도달할 수 있는 노드입니다.전체 활성 노드는 수정 상자가 가득 찬 활성 노드입니다.
각 수정에는 몇 개의 복사본(예: k)이 포함되며, 수정 상자에 대한 1개의 변경 사항이 뒤따릅니다.각 k개의 복사본을 고려합니다.각 노드는 O(1)의 공간과 시간이 소요되지만 잠재적인 함수는 1씩 감소합니다.(첫째, 복사할 노드가 가득 차서 활성화되어 있어야 함수에 기여할 수 있습니다.단, 새로운 트리에서 오래된 노드에 도달할 수 없는 경우에만 잠재적인 함수가 드롭됩니다.그러나 새로운 트리에서는 도달할 수 없는 것으로 알려져 있습니다.알고리즘의 다음 단계는 복사를 가리키도록 노드의 부모를 변경하는 것입니다.마지막으로 복사본의 수정 상자가 비어 있는 것으로 알려져 있습니다.따라서 완전한 라이브노드는 빈 라이브노드로 대체되어 " 가 1개 다운됩니다.)마지막 단계는 수정 상자를 채우고 O(1) 시간이 소요되며 †가 1씩 증가합니다.
종합하면 putting의 변화량은 δϕ =1-k이다.따라서 알고리즘은 O(k + δ)= O(1) 공간과 O(k + δ + 1) = O(1) 시간이 걸린다.
일반화된 형태의 지속성
경로 복사는 이진 검색 트리와 같은 특정 데이터 구조에서 영속성을 얻기 위한 간단한 방법 중 하나입니다.주어진 데이터 구조에서 작동하는 지속성을 구현하기 위한 일반적인 전략이 있으면 좋습니다.이를 달성하기 위해 우리는 방향 그래프 G를 고려한다.우리는 G의 각 정점 v가 포인터로 표현되는 일정한 수의 나가는 에지를 가지고 있다고 가정한다.각 정점에는 데이터를 나타내는 레이블이 있습니다.우리는 정점에 inedge(v)로 정의되는 경계된 수의 가장자리가 있다고 생각한다.우리는 G에 대해 다음과 같은 다른 조작을 허용합니다.
- CREATE-NODE(): 들어오는 모서리 또는 나가는 모서리가 없는 새 정점을 만듭니다.
- CHANGE-EDGE(v, i, u): v의 ith 엣지를 u를 가리키도록 변경합니다.
- CHANGE-LABEL(v, x): v에 저장된 데이터 값을 x로 변경합니다.
위의 조작 중 하나는 특정 시간에 실행되며 영구 그래프 표현의 목적은 임의의 시간에 G 버전에 액세스할 수 있도록 하는 것이다.이를 위해 우리는 G의 각 정점 v에 대한 표를 정의한다.테이블에는 c컬럼과 +(\ d행이 있습니다.각 행에는 발신 에지에 대한 포인터 외에 정점의 데이터를 나타내는 라벨과 연산이 실행된 시간 t가 포함됩니다.게다가 v로의 모든 착신 에지를 추적하는 어레이 입력(v)도 있습니다.테이블이 꽉 차면 d+ d 으로 새 테이블을 만들 수 있습니다.오래된 테이블이 비활성화되고 새 테이블이 활성 테이블이 됩니다.
CREATE
CREATE-NODE 호출에 의해 새로운 테이블이 생성되어 모든 참조가 null로 설정됩니다.
엣지 변경
CHANGE-EDGE(v, i, u)가 호출되었다고 가정할 경우 고려해야 할 두 가지 경우가 있습니다.
- 정점 v의 테이블에 빈 행이 있습니다: 이 경우 표의 마지막 행을 복사하고 새 정점 u를 가리키도록 정점 v의 ih 가장자리를 변경합니다.
- 정점 v의 테이블이 가득 찼습니다.이 경우 새 테이블을 만들어야 합니다.오래된 테이블의 마지막 행을 새 테이블에 복사합니다.배열의 각 정점이 생성된 새 테이블을 가리키도록 하려면 배열 inedge(v)를 루프해야 합니다.또한 그래프 G에 엣지 v,w가 존재하도록 정점 w마다 inedge(w) 내의 엔트리 v를 변경해야 한다.
라벨 변경
정점의 ith 에지를 변경하는 대신 i 라벨을th 변경하는 것을 제외하고 CHANGE-EDGE와 동일하게 작동합니다.
일반화된 지속 데이터 구조의 효율성
위에서 제안한 제도의 효율성을 찾기 위해 우리는 신용 체계로 정의된 논거를 사용한다.크레딧은 통화를 나타냅니다.예를 들어, 크레딧을 사용하여 테이블을 결제할 수 있습니다.인수에는 다음이 포함됩니다.
- 테이블 1개를 작성하려면 크레딧 1개가 필요합니다.
- CREATE-NODE에 대한 각 콜에는 2개의 크레딧이 있습니다.
- CHANGE-EDGE에 문의할 때마다 1개의 크레딧이 제공됩니다.
신용 체계는 항상 다음의 불변성을 충족해야 한다.각 활성 테이블의 각 행에는 하나의 크레딧이 저장되며 테이블에는 행의 수와 동일한 크레딧 수가 있습니다.CREATE-NODE, CHANGE-EDGE 및 CHANGE-LABEL의 세 가지 작업 모두에 불변성이 적용되는지 확인해보자.
- [CREATE-NODE] : 2개의 크레딧을 취득합니다.하나는 테이블 작성에 사용되며 다른 하나는 테이블에 추가된1개의 행에 할당됩니다.따라서 불변성이 유지됩니다.
- CHANGE-EDGE: 고려해야 할 두 가지 사례가 있습니다.첫 번째 경우는 테이블에 빈 행이 하나 이상 남아 있을 때 발생합니다.이 경우 새로 삽입된 행에 1개의 크레딧이 사용됩니다.두 번째 경우는 테이블이 꽉 찼을 때 발생합니다.이 경우 오래된 테이블이 비활성화되고 CHANGE-EDGE 호출로 취득한 크레딧과 더불어d + d) 이 새 테이블로 변환됩니다.총 d2) 이 있습니다.새 테이블을 만드는 데 1 크레딧이 사용됩니다.테이블에 추가된 새 행에 다른 크레딧이 사용되며, 나머지 d크레딧은 새 테이블을 가리킬 필요가 있는 다른 정점의 테이블을 업데이트하기 위해 사용됩니다.우리는 불변성이 유지된다고 결론짓는다.
- CHANGE-Label: CHANGE-EDGE와 동일하게 동작합니다.
요약하면 CREATE_NODE에 대한 콜이({이고 CHANGE에 대한 콜이({이면 이 된다는 것입니다.재귀 콜을 고려하지 않고 각 테이블의 는O ( )\ O ( )。테이블을 작성하려면 O( ) \ O ( { 2} }가 필요합니다.다른 노드의 inedge를 갱신함으로써 추가 d 계수가 발생합니다.따라서 일련의 조작을 완료하기 위해 필요한 작업량은 작성된 테이블 에O O를 곱한 값으로 한정됩니다.각 접근 은 O Odisplaystyle O((d)\displaystyle m엣지 및 라벨 이 필요합니다. mO ( g (){ m \ O ( (d ) } ( n d2 )+ ( d 에 CREATE - NODE 、 CHANGE - EDGE 、 CHANGE - LABEL ( )시퀀스를 n n )시퀀스를 할 수 있는 데이터 구조가 존재합니다.
영속적인 데이터 구조의 응용 프로그램
다음 요소 검색 또는 점 위치
지속성을 사용하여 효율적으로 해결할 수 있는 유용한 응용 프로그램 중 하나는 다음 요소 검색입니다.x축에 평행한 서로 교차하지 않는 세그먼트가 가정합니다 pp를 조회하여 p\p 위의 (있는 경우)를 반환할 수 있는 데이터 구조를 구축하고 싶습니다.우선 Next Element Search를 Nave 방식으로 풀고, 그 다음 지속적 데이터 구조 방식을 사용하여 해결하는 방법을 보여 줍니다.
Nave 방식
무한대로 시작하는 수직선 세그먼트에서 시작하여 왼쪽에서 오른쪽으로 선 세그먼트를 스위프합니다.이러한 세그먼트의 끝점에 도달할 때마다, 일시 정지합니다.수직선은 평면을 수직 스트립으로 분할합니다.의 라인가있는 경우 각 세그먼트에2개의 가 의 스트립을 수 있습니다스트립에서 시작 및 종료되는 세그먼트는 없습니다.모든 세그먼트가 스트립에 닿지 않거나 완전히 교차합니다.세그먼트는 위에서 아래로 정렬된 몇 가지 개체로 간주할 수 있습니다.우리가 관심을 가지는 것은 우리가 보고 있는 요점이 이 순서로 어디에 들어맞는 것이다.세그먼트의 끝점을로 정렬합니다각 에 대해 에 교차하는 부분 집합 세그먼트를 사전에 저장합니다.수직선이 선분을 스위프할 때 선분이 세그먼트의 왼쪽 끝점을 지날 때마다 사전에 추가합니다.세그먼트의 오른쪽 끝점을 통과하면 사전에서 제거합니다.모든 엔드포인트에서 사전 복사본을 저장하고 모든 x(\ x 좌표로 정렬하여 저장합니다.따라서 어떤 질의에도 응답할 수 있는 데이터 구조를 갖추고 있습니다.위의 세그먼트를 찾으려면를 어떤 복사 또는 스트립에 속하는지 알 수 있습니다. 다음를 보고 그 위의 세그먼트를 찾을 수 있습니다.따라서 x x 좌표가 또는 복사본을 찾고 y y 가 위의 세그먼트를 찾는 두 가지 이진 검색이 필요합니다.따라서 쿼리 은 O( (n ) \ ( ( n )} 。이 데이터 구조에서는 모든 세그먼트가 다른 세그먼트의 종료 전에 시작되도록 구성된 세그먼트가 있다고 가정하면 네이브 방식을 사용하여 구조체를 구축하는 데 필요한 공간이 문제가 됩니다.( ) { O ( ^ { 2}。쿼리 타임은 같지만 공간은 더 좋은 다른 영구 데이터 구조를 구축하는 방법에 대해 설명합니다.
영속적 데이터 구조화 방법
순진한 방법으로 사용되는 데이터 구조에서 시간이 걸리는 것은 스트립에서 다음 스트립으로 이동할 때마다 순서를 정렬하기 위해 사용하고 있는 데이터 구조를 스냅 샷해야 한다는 것입니다.+ 로 이동하면 si+ 1(\displaystyle 과 교차하는 세그먼트가 하나 남거나 하나 들어가는 것을 알 수 있습니다. i})와 + 의 차이가 1개의 삽입 또는 삭제에 불과한 경우 s })에서 + 1로 모든 내용을 복사하는 것은 좋지 않습니다.요령은 각 복사본이 이전 복사본과 한 번의 삽입 또는 삭제만으로 다르기 때문에 변경된 부분만 복사하면 된다는 것입니다.트리가 T T에 뿌리를 두고 있다고 가정합니다.k(\k)를 트리에 삽입하면k(\k를 하는 새로운 리프가 생성됩니다.트리의 균형을 재조정하기 위해 회전하면 경로의 노드가 k k에서T(\ T로 됩니다.k(\ k를 트리에 삽입하면 경로상의 모든 노드가k(\ k에서T(\ T로 복사됩니다.이제 트리의 2가지 버전이 생성됩니다.원본 트리는 kk를 하지 않으며 루트는 복사본인 새 트리입니다.T T의 입니다(\ k에서(\ T로의 경로를 복사해도 삽입 시간이 상수 계수 이상 늘어나지 않으므로 영구 데이터 구조에서 삽입하는 데 g 시간이 .삭제의 경우 삭제의 영향을 받는 노드를 찾아야 합니다.삭제의 영향을 받는 v마다 루트에서v v로 경로를 복사합니다.그러면 루트가 원래 트리의 루트 복사본인 새 트리가 제공됩니다.그런 다음 새 트리에서 삭제를 수행합니다.두 가지 버전의 트리로 마무리하겠습니다.k k를 하는 원래 것과 k k를 하지 않는 새로운 것. 삭제 시 루트부터v v로의 경로만 변경되므로 적절한 삭제 알고리즘은 O g ( O( n))로 실행되므로 영속적으로 삭제됩니다. 구조는 ( (n){ O ( ( n )} 삽입 및 삭제의 모든 시퀀스에 의해 사전 또는 버전 또는 의 시퀀스가 생성됩니다. i{ S _ { } 、 { } 、 S _ { 2 、 \ S _ {i} 。서 각 S _ S _ { n } each each each each each each each s s each each each each each each each each S _ { s 。 S_ 요소가m개 되어 있는 경우, Sii})의 검색은 O 를 O( g ( O( ( 쿼리 시간과 ( O ( )}{ O ( 스페이스에서 소스 코드 검색의 예를 참조하십시오.
영구 데이터 구조의 예
아마도 가장 단순한 영구 데이터 구조는 단일 링크 목록 또는 cons 기반 목록일 것입니다. 이 목록은 각각이 목록의 다음 항목에 대한 참조를 전달함으로써 형성되는 단순한 개체 목록입니다.이는 목록의 꼬리를 가져올 수 있기 때문에 지속적이며, 이는 k개의 마지막 항목을 의미하며, 그 앞에 새 노드를 추가할 수 있기 때문입니다.꼬리는 복제되지 않고 이전 목록과 새 목록 간에 공유됩니다.꼬리 부분의 내용이 변하지 않는 한, 이 공유는 프로그램에서는 보이지 않습니다.
레드-블랙 트리,[6] 스택,[7] 트리프 [8]등 많은 일반적인 참조 기반 데이터 구조를 쉽게 조정하여 영구 버전을 만들 수 있습니다.그 외 큐, 디큐 및 min-deques(최소 요소를 반환하는 추가 O(1) 연산 최소가 있음) 및 랜덤액세스 디큐(이들 중 가장 많은 경우 로그와 복잡도가 하위 선형인 랜덤액세스 추가 연산)를 포함한 확장 기능이 약간 더 필요합니다.
파괴적인[clarification needed] 조작을 사용하는 영속적인 데이터 구조도 존재하기 때문에 순수하게 기능하는 언어(상태나 IO와 같은 특수한 모나드 외부의 Haskell 등)에서는 효율적으로 구현할 수 없지만 C나 Java와 같은 언어에서는 가능합니다.이러한 유형의 데이터 구조는 종종 다른 설계로 피할 수 있습니다.순수하게 영속적인 데이터 구조를 사용하는 것의 주된 이점 중 하나는 멀티 스레드 환경에서 더 잘 동작한다는 것입니다.
링크 리스트
단일 링크 리스트는 기능 [9]언어의 기본적인 데이터 구조입니다.Haskell과 같이 ML에서 파생된 일부 언어는 완전히 기능합니다.이는 목록 내의 노드가 할당되면 아무것도 참조하지 않을 때 가비지 컬렉터에 의해 수정, 복사, 참조 또는 파기할 수 없기 때문입니다.(ML 자체는 완전히 기능하는 것이 아니라 비파괴 리스트 조작 서브셋을 지원하는 것에 주의해 주십시오.이것은 에서도 마찬가지입니다.스킴이나 라켓 등의 기능적 언어 사투리.
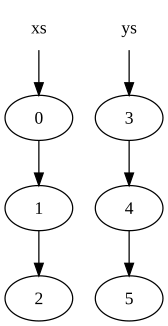
다음 두 가지 목록을 고려합니다.
xs = [0, 1, 2] ys = [3, 4, 5]
메모리에는 다음과 같이 표시됩니다.
여기서 원은 목록의 노드를 나타냅니다(다른 노드에 대한 포인터인 노드의 두 번째 요소를 나타내는 화살표).
이제 두 목록을 연결합니다.
zs = xs + + ys
그럼, 다음의 메모리 구조가 됩니다.
목록에 있는 노드가xs복사는 완료되었지만 노드에는ys공유됩니다.그 결과, 원래의 리스트(xs그리고.ys)는 변경되지 않은 상태로 유지됩니다.
복사하는 이유는 마지막 노드가xs(원래 값을 포함하는 노드)2)는 의 시작을 가리키도록 변경할 수 없습니다.ys그 때문에, 그 값이 바뀌기 때문입니다.xs.
나무들
바이너리 검색 [9]트리에 있는 모든 노드에 왼쪽 서브트리에 포함된 모든 서브노드의 값이 노드에 저장된 값보다 작거나 같고 오른쪽 서브트리에 포함된 서브노드의 값이 노드에 저장된 값보다 크다는 재귀적 불변성이 있다고 가정합니다.
예를 들어 데이터 세트
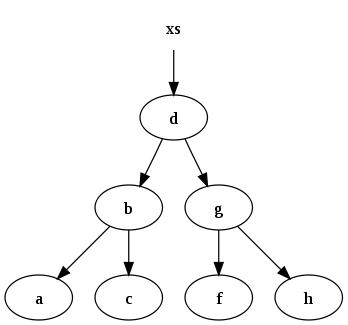
xs = [a, b, c, d, f, g, h]
는 다음 이진 검색 트리로 표시될 수 있습니다.
이진 트리에 데이터를 삽입하고 불변성을 유지하는 함수는 다음과 같습니다.
재밌어요 삽입하다 (x, E) = T (E, x, E) 삽입하다 (x, s ~하듯이 T (a, y, b)) = 한다면 x < > y 그리고나서 T (삽입하다 (x, a), y, b) 또 다른 한다면 x > y 그리고나서 T (a, y, 삽입하다 (x, b)) 또 다른 s 실행 후
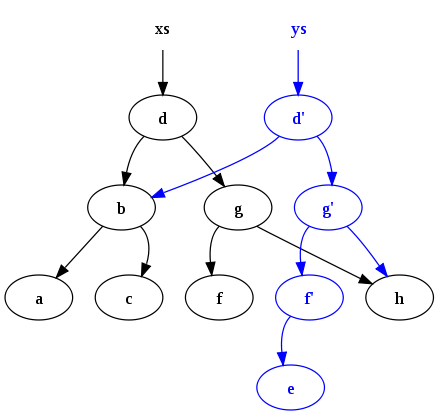
ys = 삽입("e", xs") 다음의 설정이 작성됩니다.
주의: 첫 번째, 원래 트리(xs)는 계속됩니다.둘째, 많은 공통 노드가 오래된 트리와 새로운 트리에서 공유됩니다.이러한 지속성과 공유는 라이브 참조가 없는 노드를 자동으로 해방하기 위해 어떤 형태의 가비지 컬렉션(GC)이 없으면 관리하기 어렵습니다.이 때문에 GC는 기능 프로그래밍 언어에서 일반적으로 볼 수 있는 기능입니다.
영속적 해시 어레이 매핑
영속적 해시 어레이 매핑트라이는 해시 어레이 매핑트라이의 특수한 변형으로, 업데이트 시 이전 버전의 해시 어레이를 유지합니다.범용 영속적 지도 데이터 [10]구조를 구현하기 위해 자주 사용됩니다.
해시 배열 매핑 시도는 필 백웰이 2001년에 발표한 "Ideal Hash Trees"라는 논문에서 처음 설명되었습니다.이 문서에서는 "삽입, 검색 및 삭제 시간은 작고 일정하며 키 세트 크기에 관계없이 운영은 O(1)입니다.인서트, 검색, 삭제 조작의 최악의 시간을 최소한으로 억제할 수 있습니다.또, 검색의 성공보다 누락의 코스트를 삭감할 수 있습니다」.[11]그런 다음 Rich Hickey가 Clojure 프로그래밍 언어로 사용할 [12]수 있도록 이 데이터 구조를 수정했습니다.
개념적으로 해시 배열 매핑 시도는 노드를 계층적으로 저장하고 특정 요소에 대한 경로를 따라 노드를 검색한다는 점에서 일반 트리와 유사합니다.주요 차이점은 Hash Array Mapped Tries는 처음에 해시 함수를 사용하여 검색 키를 (보통 32비트 또는 64비트) 정수로 변환한다는 것입니다.그런 다음 해당 정수의 바이너리 표현 슬라이스를 사용하여 트리의 각 레벨에서 스파스 배열로 인덱싱하여 트리 다운 경로를 결정합니다.트리의 리프 노드는 해시 테이블을 구성하는 데 사용되는 버킷과 유사하게 동작하며 해시 [10]충돌에 따라 여러 후보가 포함될 수도 있고 포함되지 않을 수도 있습니다.
영구 해시 배열 매핑 시도 구현의 대부분은 구현에 분기 계수 32를 사용합니다.즉, 실제로는 영속적인 해시 배열 맵트리에 삽입, 삭제 및 룩업이 O(log n)의 계산 복잡도를 갖습니다.대부분의 어플리케이션에서는 매우 많은 수의 엔트리가 필요하기 때문에 이들 엔트리가 12단계 이상 [13]진행됩니다.
프로그래밍 언어에서의 사용
하스켈
Haskell은 순수 기능 언어이므로 돌연변이를 허용하지 않습니다.따라서 언어 내의 모든 데이터 구조는 기능적 [14]의미론으로는 데이터 구조의 이전 상태를 보존하지 않는 것이 불가능하기 때문에 영구적이다.이는 데이터 구조의 이전 버전을 무효로 만드는 데이터 구조를 변경하면 참조 투명성이 위반되기 때문입니다.
Haskell은 표준 라이브러리에서 링크 목록,[15] 맵(크기 균형 [16]트리로 구현)[18] 및 세트[17] 등에 대한 효율적인 영구 구현을 제공합니다.
클로쥬르
Lisp 패밀리의 많은 프로그래밍 언어와 마찬가지로 Clojure는 링크드 리스트의 구현을 포함하고 있지만 다른 방언과 달리 링크드 리스트의 구현은 [19]관례에 따라 지속적이지 않고 지속성을 강요하고 있습니다.또한 Clojure는 지속적인 해시 배열 매핑 시도를 기반으로 영속적인 벡터, 맵 및 세트를 효율적으로 구현합니다.이러한 데이터 구조는 Java 컬렉션 [20]프레임워크의 필수 읽기 전용 부분을 구현합니다.
Clojure 언어 설계자들은 변이 가능한 데이터 구조보다 영속적인 데이터 구조를 사용하는 것을 지지합니다.왜냐하면 이러한 데이터 구조에는 값싼 별칭을 가진 스레드 간에 자유롭게 공유할 수 있고, 제작이 용이하며,[21] 언어에 의존하지 않는 이점이 있기 때문입니다.
이러한 데이터 구조는 데이터 레이스를 회피하고 원자적인 비교와 [22]의미론을 교환하는 작업을 쉽게 재시도할 수 있기 때문에 Clojure가 병렬 컴퓨팅을 지원하는 기반을 형성합니다.
느릅나무
Elm 프로그래밍 언어는 Haskell과 같이 기능적으로만 작동하므로 모든 데이터 구조가 필요에 따라 영구적입니다.여기에는 링크된 목록의 영구 구현과 [23]영구 배열, 사전 및 세트가 포함됩니다.
Elm은 Elm 데이터의 영속성을 활용하는 커스텀 가상 DOM 구현을 사용합니다.2016년 현재 Elm 개발자에 따르면 이 가상 DOM은 Elm 언어가 인기 있는 JavaScript 프레임워크인 React, Ember 및 [24]Angular보다 HTML을 더 빠르게 렌더링할 수 있도록 합니다.
자바
자바 프로그래밍 언어는 특별히 기능하지 않습니다.그럼에도 불구하고 핵심 JDK 패키지 java.util.concurrent에는 CopyOnWriteArrayList 및 CopyOnWriteArraySet이 포함되어 있습니다.이것은 Copy-OnWrite 기술을 사용하여 구현되는 영속적인 구조입니다.단, Java에서의 일반적인 동시 맵 실장 ConcurrentHashMap은 영속적이지 않습니다.완전 영속적인 컬렉션은 서드파티 라이브러리 또는 기타 JVM 언어로 사용할 수 있습니다.
자바스크립트
이 섹션은 독자들에게 혼란스럽거나 불분명할 수 있습니다.(2021년 (템플릿메시지 및 에 대해 ) |
널리 사용되는 JavaScript 프런트 엔드 프레임워크인 React는 JavaScript 라이브러리 Redx를 구현한 Flux [25][26]아키텍처를 구현하는 상태 관리 시스템과 함께 자주 사용됩니다.Redux 라이브러리는 Elm 프로그래밍 언어에서 사용되는 상태 관리 패턴에서 영감을 얻었으며, 이는 사용자가 모든 데이터를 [27]영구적인 것으로 취급해야 함을 의미합니다.따라서 Redux 프로젝트에서는 사용자에게 강제적이고 효율적인 영구 데이터 구조를 위해 라이브러리를 사용할 것을 권장합니다.이것에 의해, 통상의 JavaScript [28]오브젝트를 비교하거나 카피를 작성할 때보다 뛰어난 퍼포먼스를 얻을 수 있다고 합니다.
이러한 영구 데이터 구조 Imponable.js 라이브러리는 Clojure와 Scala가 [29]제공하고 보급한 데이터 구조를 기반으로 합니다.Redux 문서에서는 강제 [28]불변성을 제공할 수 있는 라이브러리 중 하나로 언급되어 있습니다.Mori.js는 Clojure와 유사한 데이터 구조를 JavaScript로 [30]가져옵니다.Immer.js는 "현재 상태를 변환하여 다음 불변의 상태를 만든다"는 흥미로운 접근 방식을 제공합니다.[31] Immer.js는 네이티브 JavaScript 개체와 비효율적인 영구 데이터 구조를 사용하기 때문에 데이터 크기가 클 때 성능 문제가 발생할 수 있습니다.
프롤로그
프롤로그 용어는 당연히 불변하기 때문에 데이터 구조는 일반적으로 영속적인 데이터 구조입니다.퍼포먼스는 Prolog [32]시스템에서 제공하는 공유 및 가비지 수집에 따라 달라집니다.검색 공간이 폭발적으로 증가하기 때문에 논그라운드 프롤로그 용어의 확장이 항상 가능한 것은 아닙니다.목표가 지연되면 문제가 완화될 수 있습니다.
단, 일부 Prolog 시스템에서는 setarg/3와 같은 파괴적인 조작을 제공하고 있습니다.이것은, 카피 유무와 상태 변경의 백트래킹 유무에 관계없이, 다른 플레이버로 제공될 수 있습니다.setarg/3가 제약 [33]해결사처럼 새로운 선언적 레이어를 제공하는 데 사용되는 경우가 있습니다.
스칼라
Scala 프로그래밍 언어는 "Object-Functional Style"[34]을 사용하여 프로그램을 구현하기 위한 영구 데이터 구조의 사용을 촉진합니다.Scala에는 Linked Lists, Red-Black Tree, Clojure에서 [35]소개된 영구 해시 배열 매핑 시도 등 많은 영구 데이터 구조의 구현이 포함되어 있습니다.
가비지 컬렉션
영구 데이터 구조는 종종 데이터 구조의 후속 버전이 기초가[36] 되는 메모리를 공유하는 방식으로 구현되기 때문에 이러한 데이터 구조의 인체공학적인 사용은 일반적으로 참조 카운트 또는 [37]마크 앤 스위프와 같은 자동 가비지 수집 시스템을 필요로 한다.영구 데이터 구조를 사용하는 일부 플랫폼에서는 가비지 컬렉션을 사용하지 않는 것이 좋습니다. 가비지 컬렉션을 사용하면 메모리 누수가 발생할 수 있지만 경우에 따라서는 애플리케이션의 [38]전체 성능에 긍정적인 영향을 미칠 수 있습니다.
「 」를 참조해 주세요.
레퍼런스
- ^ a b Driscoll JR, Sarnak N, Sleator DD, Tarjan RE (1986). "Making data structures persistent". Proceedings of the eighteenth annual ACM symposium on Theory of computing - STOC '86. Proceeding STOC '86. Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing. pp. 109–121. CiteSeerX 10.1.1.133.4630. doi:10.1145/12130.12142. ISBN 978-0-89791-193-1. S2CID 364871.
- ^ a b Kaplan, Haim (2001). "Persistent data structures". Handbook on Data Structures and Applications.
- ^ Conchon, Sylvain; Filliâtre, Jean-Christophe (2008), "Semi-persistent Data Structures", Programming Languages and Systems, Lecture Notes in Computer Science, vol. 4960, Springer Berlin Heidelberg, pp. 322–336, doi:10.1007/978-3-540-78739-6_25, ISBN 9783540787389
- ^ Tiark, Bagwell, Philip Rompf (2011). RRB-Trees: Efficient Immutable Vectors. OCLC 820379112.
- ^ Brodal, Gerth Stølting; Makris, Christos; Tsichlas, Kostas (2006), "Purely Functional Worst Case Constant Time Catenable Sorted Lists", Lecture Notes in Computer Science, Springer Berlin Heidelberg, pp. 172–183, CiteSeerX 10.1.1.70.1493, doi:10.1007/11841036_18, ISBN 9783540388753
- ^ Neil Sarnak; Robert E. Tarjan (1986). "Planar Point Location Using Persistent Search Trees" (PDF). Communications of the ACM. 29 (7): 669–679. doi:10.1145/6138.6151. S2CID 8745316. Archived from the original (PDF) on 2015-10-10. Retrieved 2011-04-06.
- ^ Chris Okasaki. "Purely Functional Data Structures (thesis)" (PDF).
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ Liljenzin, Olle (2013). "Confluently Persistent Sets and Maps". arXiv:1301.3388. Bibcode:2013arXiv1301.3388L.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ a b 이 예는 오카사키에서 따온 것입니다.참고 문헌을 참조하십시오.
- ^ a b BoostCon (2017-06-13), C++Now 2017: Phil Nash "The Holy Grail!? A Persistent Hash-Array-Mapped Trie for C++", archived from the original on 2021-12-21, retrieved 2018-10-22
- ^ Phil, Bagwell (2001). "Ideal Hash Trees".
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ "Are We There Yet?". InfoQ. Retrieved 2018-10-22.
- ^ Steindorfer, Michael J.; Vinju, Jurgen J. (2015-10-23). "Optimizing hash-array mapped tries for fast and lean immutable JVM collections". ACM SIGPLAN Notices. 50 (10): 783–800. doi:10.1145/2814270.2814312. ISSN 0362-1340. S2CID 10317844.
- ^ "Haskell Language". www.haskell.org. Retrieved 2018-10-22.
- ^ "Data.List". hackage.haskell.org. Retrieved 2018-10-23.
- ^ "Data.Map.Strict". hackage.haskell.org. Retrieved 2018-10-23.
- ^ "Data.Set". hackage.haskell.org. Retrieved 2018-10-23.
- ^ "Performance/Arrays - HaskellWiki". wiki.haskell.org. Retrieved 2018-10-23.
- ^ "Clojure - Differences with other Lisps". clojure.org. Retrieved 2018-10-23.
- ^ "Clojure - Data Structures". clojure.org. Retrieved 2018-10-23.
- ^ "Keynote: The Value of Values". InfoQ. Retrieved 2018-10-23.
- ^ "Clojure - Atoms". clojure.org. Retrieved 2018-11-30.
- ^ "core 1.0.0". package.elm-lang.org. Retrieved 2018-10-23.
- ^ "blog/blazing-fast-html-round-two". elm-lang.org. Retrieved 2018-10-23.
- ^ "Flux Application Architecture for Building User Interfaces". facebook.github.io. Retrieved 2018-10-23.
- ^ Mora, Osmel (2016-07-18). "How to handle state in React". React Ecosystem. Retrieved 2018-10-23.
- ^ "Read Me - Redux". redux.js.org. Retrieved 2018-10-23.
- ^ a b "Immutable Data - Redux". redux.js.org. Retrieved 2018-10-23.
- ^ "Immutable.js". facebook.github.io. Archived from the original on 2015-08-09. Retrieved 2018-10-23.
- ^ "Mori".
- ^ "Immer". GitHub. 26 October 2021.
- ^ Djamboulian, Ara M.; Boizumault, Patrice (1993), The Implementation of Prolog - Patrice Boizumault, ISBN 9780691637709
- ^ The Use of Mercury for the Implementation of a Finite Domain Solver - Henk Vandecasteele, Bart Demoen, Joachim Van Der Auwera, 1999
- ^ "The Essence of Object-Functional Programming and the Practical Potential of Scala - codecentric AG Blog". codecentric AG Blog. 2015-08-31. Retrieved 2018-10-23.
- ^ ClojureTV (2013-01-07), Extreme Cleverness: Functional Data Structures in Scala - Daniel Spiewak, retrieved 2018-10-23[죽은 유튜브 링크]
- ^ "Vladimir Kostyukov - Posts / Slides". kostyukov.net. Retrieved 2018-11-30.
- ^ wiki.c2.com http://wiki.c2.com/?ImmutableObjectsAndGarbageCollection. Retrieved 2018-11-30.
{{cite web}}:누락 또는 비어 있음title=(도움말) - ^ "The Last Frontier in Java Performance: Remove the Garbage Collector". InfoQ. Retrieved 2018-11-30.


 CHANGE에 대한 콜이
CHANGE에 대한 콜이


 필요합니다.다른 노드의 inedge를 갱신함으로써 추가 d 계수가 발생합니다.따라서 일련의 조작을 완료하기 위해 필요한 작업량은 작성된 테이블
필요합니다.다른 노드의 inedge를 갱신함으로써 추가 d 계수가 발생합니다.따라서 일련의 조작을 완료하기 위해 필요한 작업량은 작성된 테이블 






 정렬합니다
정렬합니다
 보고 그 위의 세그먼트를 찾을 수 있습니다.따라서 x
보고 그 위의 세그먼트를 찾을 수 있습니다.따라서 x

 이동하면 si
이동하면 si

 루트에서v
루트에서v