일차 선 상수

1차 선로 상수는 구리선 쌍과 같은 전도성 전송선의 특성을 선로의 물리적 전기적 특성에 대해 설명하는 파라미터입니다.1차 선로 상수는 전송 선로에만 관련되며, 2차 선로 상수와 대조되어야 하며, 2차 선로 상수는 이들로부터 도출할 수 있으며 보다 일반적으로 적용할 수 있습니다.예를 들어 2차 라인 상수는 도파관의 특성을 구리 라인에 비교하는 데 사용할 수 있지만 1차 상수는 도파관에 의미가 없습니다.

상수는 도체 저항 및 인덕턴스, 절연체 캐패시턴스 및 컨덕턴스이며, 이는 각각 기호 R, L, C 및 G로 지정됩니다.상수는 단위 길이당 단위로 열거됩니다.이러한 소자의 회로 표현에는 분산 소자 모델이 필요하며, 따라서 회로 분석에 미적분을 사용해야 합니다.분석 결과 특성 임피던스와 전파 상수의 2차 상수를 도출하기 위해 결합될 수 있는 두 개의 1차 선형 편미분 방정식의 시스템이 생성됩니다.

많은 특수한 경우 특히 단순한 솔루션과 중요한 실용적 응용이 있습니다.저손실 케이블은 L과 C만 분석에 포함하면 되기 때문에 짧은 길이의 케이블에 도움이 됩니다.트위스트 페어 전화 회선등의 저주파 애플리케이션은, R 와 C 만이 지배하고 있습니다.RF 동축 케이블과 같은 고주파 애플리케이션은 L 및 C에 의해 지배됩니다.왜곡을 방지하기 위해 로드된 선은 분석에 4가지 요소가 모두 필요하지만 단순하고 우아한 솔루션을 제공합니다.

상수

4개의 주요 선 상수가 있지만 일부 상황에서는 무시할 수 있을 정도로 작아서 분석을 단순화할 수 있습니다.이들 4개의 기호와 단위는 다음과 같습니다.

이름.	기호.	단위	단위 기호
루프 저항	R	미터당 옴	Ω/m
루프 인덕턴스	L	미터당 암탉	H/M
절연체 캐패시턴스	C	미터당 패러드	F/m
절연체 전도율	G	미터당 지멘스	S/m

R과 L은 라인과 직렬로 연결된 원소이며(도체의 특성이기 때문에), C와 G는 라인을 분리하는 원소이다(도체 간 유전체 재료의 특성이기 때문에).G는 유전체를 통한 누출 전류를 나타내며 대부분의 케이블은 매우 작습니다.루프라는 단어는 두 도체의 저항과 인덕턴스를 고려해야 함을 강조하기 위해 사용됩니다.예를 들어 회선이 각각 25MΩ/m의 저항을 갖는 2개의 동일한 와이어로 구성되어 있는 경우 루프 저항은 50MΩ/m의 2배가 됩니다.상수의 값이 매우 작기 때문에 제조업체는 미터 당이 아닌 킬로미터 당 값을 견적하는 것이 일반적입니다. 영어권에서는 "마일 당"도 ^[1][2]사용할 수 있습니다.

상수라는 단어는 오해의 소지가 있습니다.즉, 물질 상수이지만 빈도에 따라 다를 수 있습니다.특히 R은 피부 효과의 영향을 많이 받는다.또, G는 오디오 주파수에서는 거의 영향이 없지만, 고손실 접선에 의해 케이블에 사용되는 유전체 재료의 상당수는 고주파에서 현저한 손실을 일으킬 수 있다.G로 인한 손실을 방지하기 위해 UHF에서 사용하도록 설계된 많은 케이블은 공기 절연 또는 폼 절연(가상 공기 절연)^[3]되어 있습니다.이 컨텍스트에서 상수의 실제 의미는 파라미터가 거리에 따라 일정하다는 것입니다.즉, 선은 세로 방향으로 균질하다고 가정됩니다.이 상태는 ^[4]현재 사용되고 있는 대부분의 전송 회선에 해당됩니다.

일부 일반적인 케이블의 일반적인 값

지정	케이블 형태	어플	R	L†	G	C	Z0
			Ω/km	μH/km	nS/km	nF/km	Ω
CAT5[5]	트위스트 페어	data 전송	176	490	2 미만	49	100
CAT5e[6]	트위스트 페어	data 전송	176		2 미만		100
CW1308[7]	트위스트 페어	텔레포니	98		20 미만
RG59[8]	동축	비디오	36	430		69	75
RG59[9]	동축 (표준 유전체)	비디오	17	303		54	75
RG58[10][11]	동축	무선 주파수	48	253	0.01 미만	101	50
저손실[12]	동축 (폼 유전체)	무선 주파수 송신기 피드	2.86	188		75	50
DIN VDE 0816[13]	스타 쿼드	텔레포니 (줄바꿈)	31.8		0.1 미만	35

§ 제조업체는 일반적으로 데이터 시트에서 인덕턴스 값을 생략합니다.이러한 값 중 일부는 Z ${\displaystyle {{0\mathrm{}}_{}}^{}}$ ${\displaystyle {{}_{}}^{\mathrm{}}}$ ${\displaystyle {}^{}L}$ /$$ ${\displaystyle$ \$scriptstyle {Z_{$0}} =$L/$C$\}$의 캐패시턴스 및 특성 임피던스 수치를 통해 추정됩니다.

회선 표현

라인 상수는 단순히 회선 내의 일괄 소자로 나타낼 수 없습니다.분산 소자로 기술해야 합니다.예를 들어 캐패시턴스의 "조각"은 저항의 "조각" 사이에 있습니다.R과 C는 아무리 많은 조각으로 분할되어 있어도 회로를 적절히 표현하기 위해서는 항상 더 세분화되어야 하며, 분할 후에는 회로 내의 메시 수가 증가해야 합니다.이것은 그림 1에 도식으로 나타나 있습니다.회로를 제대로 표현하기 위해서는 소자를 무한히 작게 만들어 각 소자가 선을 따라 분포되도록 해야 합니다.극소 ${\displaystyle \mathrm{거리}}$ d$x$ \$displaystyle$ \$scriptstyle$$$dx}의 ^[14]극소 요소는 다음과 같습니다.

${\displaystyle dL=\lim _{\delta x}(L\delta x)=Ldx}$

${\displaystyle dR=\lim _{\delta x}(R\delta x)=Rdx}$

${\displaystyle dC=\lim _{\delta x}(C\delta x)=Cdx}$

${\displaystyle dG=\lim _{\delta x}(G\delta x)=Gdx}$

이러한 요소를 일반 직렬 임피던스, Z 및 션트 어드미턴스, Y 요소로 롤업하는 것이 분석 목적에 편리합니다.

${\displaystyle d}$ Z ${\displaystyle =}$ (${\displaystyle R}$ + ${\displaystyle i}$ ${\displaystyle l}$L )${\displaystyle d}$ x ${\displaystyle =}$ ${\displaystyle Z}$ ${\displaystyle dx}$, \ $displaystyle dZ$= ( $R$+ i \$메가$L )$dx$ =$Zdx$, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

$\displaystyle dY=(G+i\Omega C)dx=Ydx,}$

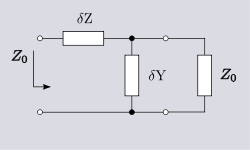
이 네트워크(그림 2)를 분석하면 $전파상수{\displaystyle }$ ${\\$ \$gamma$}, (실제 및 가상부분은 $,$ α$\displaystyle \scriptstyle$ \alpha $\}$ 및$위상변화상수{\displaystyle }$ $β\displaystyle$ \beta$\}$가 됩니다.ely) 및 특성 임피던스 Z $(\$은 일반적으로 R$$(\$displaystyle \scriptstyle R_{0$과 가상의 $X{\displaystyle {}_{}}$(\$displaystyle \scriptstyle X_{0$을 가지며, 총 4개의 2차 상수가 4개의 상수로 구성됩니다.s. 1차 상수가 그렇지 않은 이상적인 상황에서도 보통 주파수에 따라 상당히 크게 달라지기 때문에 2차 상수에 대한 용어 상수는 더욱 오해의 소지가 있습니다.이는 회로 내의 리액턴스( ${\displaystyle l}$L \ $displaystyle$ \$scriptstyle$ \ $obega$$$L$$）${\displaystyle }$$1$ /1${\displaystyle }$/ ( C$$) \ $displaystyle \scriptstyle$1/ ( ( $obega$ C$$)$$))이$$${\$에 의존하기 때문에$α$가 $되는{\displaystyle }$ 프라이머리 상수의 특정 값을 선택할 수 있습니다.$tyle \scriptstyle \alpha }$ 및$$ ${\displaystyle {Z\mathrm{}}_{}}$ 0$(\$은 ${\$ {\$displaystyle \obe$}($$헤비사이드 조건)$과$는 독립적이지만 $이{\displaystyle }$ 경우에도$as{\displaystyle }$ {\$displaystyle \scriptstyle$ \$betyle$에 정비례하는β가 존재합니다.1차 상수, 즉 "변수"의 의미는 2차 상수가 ^[14][15][16]주파수에 의존하지 않는다는 것이 아니라 선을 따라 거리에 따라 달라지지 않는다는 것입니다.

특성 임피던스

전송 라인의 특성 임피던스 ${\displaystyle {Z\mathrm{}}_{}}$ 0$(\$은 무한히 긴 라인을 바라보는 임피던스로 정의됩니다.이러한 선은 입사파가 반영되는 끝까지 도달하지 않기 때문에 반사를 반환하지 않습니다.회선의 길이가 한정되어 있는 것을 생각하면, 회선의 나머지 부분은 동등한 회선으로서 Z $(\$으로 $대체$할 수 있습니다.이는 선의 나머지 부분이 여전히 무한히 길기 때문에 원래 선과 동일하기 때문입니다.유한 세그먼트가 매우 짧은 경우 등가회선에서는 ${\displaystyle d}$ Z$(\$의 $1개{\displaystyle }$ 요소와 d$$(\$displaystyle \scriptstyle dY$의 1개로 구성된 L-네트워크에 의해 모델링됩니다.나머지 부분은 ${\displaystyle {Z\mathrm{}}_{}}$0(\$displaystyle \scriptstyle Z_{0$로 지정됩니다.그 결과, 그림 3에 나타낸 네트워크가 됩니다.이 네트워크는 통상적인 네트워크 분석 ^[17][18]정리를 사용하여 Z $(\displaystyle$ \$scriptstyle Z_{$0$$})에 대해 분석할 수 있습니다.

${\displaystyle Z_{0}=\delta Z+{\frac {Z_{0}}{1+Z_{0}\delta Y}}$

다시 주선해서

$({displaystyle {Z_{0}})^2}-Z_{0}\delta Z=blac {\delta Y})$

양측의 한계를 극복하다

$\displaystyle \lim _{\delta x\to 0}({Z_{0}}^2}-Z_{0}\delta Z)={Z_{0}}^{2}=black{dZ}{dY}}}$

그리고 선이 세로 방향으로 균질하다고 가정했기 때문에

${\displaystyle {Z_{0}}^2}=flac {Z}{Y}}}$

전파 상수

라인 아래쪽(즉 등가회로의 한 섹션 이후) 거리 ${\displaystyle \theta }$ x$(\$x)에$$ 대한 라인 입력 전압의 비율은 표준 분압 계산에 의해 결정됩니다.특성 임피던스 계산과 같이 오른쪽 행의 나머지 부분은 Z $(\$^[19][20]으로 대체됩니다.

$({displaystyle {V_{\mathrm {i}}}{V_{x1}}={frac Z+{Z_{0}/\delta Y}{Z_{0}+1/\delta Y}}}{\frac {Z_{0}/{0}) {\delta Y}{0})$

각 극소 섹션은 전압 강하에 동일한 계수를 곱합니다.n개의$$\$displaystyle \scriptstyle$n 섹션$$ 후 $전압비$는 다음과 같습니다.

${\displaystyle {V_{\mathrm {i}}}{V_{xn}}=\left(1+{\frac Z}{Z_{0}}+\delta Z\delta Y\오른쪽)^{n}}$

x$(\$ x$)$ $거리$에서 섹션의 수는 x${\displaystyle }$/ ${\displaystyle x}$x$(\displaystyle$ \$scriptstyle$ x$/\delta$x)이므로 다음과 같습니다.

${\displaystyle {V_{\mathrm {i}}}{V_{xn}}=\left(1+{\frac Z}{Z_{0}}+\delta Y\right)^{\frac {x}{\frac x}}}$

${\displaystyle \mathrm{limit}}$ x $→$ ${\displaystyle 0}$ \ $displaystyle$\ $scriptstyle$\ $script$ style $x$\ $to$ 0$\}$ as 、

${\displaystyle {V_{\mathrm {i}}}{V_{x}}=\lim _{\mathrm {i}}{V_{xn}}=\lim _{\lim x\to 0}\left (1+\frac {i}) Z {\lim}$

2차 항 ${\displaystyle Z}$ ${\displaystyle y}$ Y {$displaystyle$\$script$style \ $delta$Z \ $delta$ Y$$}가$$ 제한 내에서 사라지기 때문에 정확성을 잃지 않고 쓸 수 있습니다.

${\displaystyle {V_{\mathrm {i}}}{V_{x}}=\lim _{\lim x\to 0}\left (1+{\frac Z}{Z_{0}}\right}^{\frac {x}{\frac x}}}}}}$

수학적 정체성과 비교해서

$\displaystyle e^{x}\equiv \lim _{p\to\infty}(1+1/p)^{px}$

수율,

${\displaystyle V_{\mathrm {i}}=V_{x}e^{\frac {Z}{Z_{0}}x}}$

전파 상수의 정의로 볼 때론

${\displaystyle V_{\mathrm {i}}=V_{x}e^{\gamma x},\!}$

이런 이유로,

$\displaystyle \displays = frac {Z} {Z_{0}} = sqrt {Z}Y}}}$

특수한 경우

이상적인 전송 선로

이상적인 전송 선로에는 손실이 없으며, 이는 저항 요소가 0임을 의미합니다.또한 순수하게 실제(저항적) 특성 임피던스도 발생합니다.이상적인 선은 실제로 실현될 수 없지만, 많은 상황에서 유용한 근사치입니다.예를 들어 짧은 회선을 스터브 등의 회선 컴포넌트로 사용하는 경우에는 특히 그렇습니다.짧은 라인은 손실이 매우 적기 때문에 이를 무시하고 이상적인 라인으로 취급할 수 있습니다.이러한 상황에서 2차 상수는 다음과 같다.^[21]

$(\displaystyle\displaystyle=i\mega {LC})$

$\displaystyle \alpha = 0,$

$\displaystyle \displays =\mega {LC}}$

$({displaystyle Z_{0}=sqrt {frac {L} {C}})$

트위스트 페어

일반적으로 오디오 주파수 또는 낮은 데이터 레이트에 사용되는 트위스트 페어 케이블에는 R과 C가 지배하는 라인 상수가 있습니다.유전 손실은 보통 이러한 주파수에서 무시할 수 있으며 G는 0에 가깝습니다.또한 충분히 낮은 $주파수$에서 R${\displaystyle l}$L \ $displaystyle$ \$scriptstyle R\g$ \ $obega$L도$$ 무시할 수 있습니다.그러한 상황에서 ^[22]이차 상수는

$\displaystyle \gamma \약 \sqrt {i\obega CR}}$

$\displaystyle \alpha \apprough \sqrt \frac \mega CR } {2} }$

$(표시 스타일) 약 {\sqrt {\frac {\obe CR} {\sqrt}$

${\displaystyle Z_{0}\약 {\frac {R}{i\opha C}}=sqrt {\frac {R}{2\opha C}}-i{\sqrt {R}{2\opha C}}}}$

이 케이블 유형의 감쇠는 주파수에 따라 증가하여 파형이 왜곡됩니다.주파수와 함께$$β ${\style$ \$scriptstyle$ \$beta}$의 변동도 분산이라고 불리는 유형의 왜곡을 일으킵니다.산포를 피하기 위해서는$$β$(\displaystyle\scriptstyle\beta)$가$${\(\$displaystyle\scriptstyle\$mega$)$에 정비례해야 하지만 $실제로$는 ${\(\$ 및$$ 산포 결과에 비례해야 합니다.${\displaystyle {Z\mathrm{}}_{}}$ 0$(\$도 주파수에 따라 다르며 부분적으로 반응합니다.이러한 특징들은 모두 저항성 회선 종단으로부터의 반사의 원인이 됩니다.이것은 또 다른 바람직하지 않은 결과입니다.이 타입의 케이블에 대해 인용되는 공칭 임피던스는, 이 경우, 1개의 스폿 주파수만으로 유효하며, 통상은 800Hz 또는 1kHz로 ^[23][24]인용됩니다.

동축 케이블

충분히 높은 주파수(중파 무선 주파수 또는 높은 데이터 레이트)로 동작하는 케이블은 R$$L \ $displaystyle$ \$$$script style$ R $\ ll$ \ $obmega$ L$$$g$ G ${\displaystyle c}$C \ $displaystyle \ ll$ \ c C$$${\displaystyle .}$ $itionsitionsitionsitionsitions{\displaystyle }$ the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the이것은, 어느 케이블에서도 주파수가 증가하기 때문에, 최종적으로 그렇게 될 필요가 있습니다.이러한 조건 하에서 R과 G는 (케이블 손실 계산의 목적을 제외하고) 무시될 수 있으며 2차 상수는 다음과 ^[25]같이 된다.

$\displaystyle \gamma \apprough i\mega \sqrt {LC}}$

$\displaystyle \alpha \approx {2\sqrt {LC}}=sfrac {1}{2}}\left(Z_{0}G+{Z_{0}}\right)\약 {frac {R}{2Z_0}}}\약 {frac {2}}}}}}$

$\displaystyle \beta \약 \mega \sqrt {LC}}$

${\displaystyle Z_{0}\약 {\sqrt {\frac {L}{C}}}}$

로드된 라인

로드된 라인은 의도적으로 인덕턴스를 높인 라인입니다.이것은 케이블에 철 또는 기타 자성 금속을 추가하거나 코일을 추가하는 방법으로 이루어집니다.그 목적은 라인이 헤비사이드 조건을 충족하도록 하는 것입니다.이는 주파수에 의존하는 감쇠 및 분산으로 인한 왜곡을 ${\displaystyle {제거}_{}}$하고$$Z 0$(\displaystyle$ \$scriptstyle Z_{$0$$})이 일정하고 저항성이 $있음$을 보증하는 것입니다.2차 상수는 다음과 ^[26]같이 1차 상수와 관련이 있습니다.

${\displaystyle\displayrt {RG}}+i\Omega {lc}}$

${\displaystyle \alpha = {RG}}$

$\displaystyle \displays =\mega {LC}}$

$({displaystyle Z_{0}=sqrt {Frac {L} {C}}=sqrt {Frac {R} {G}})$

속도

전파 속도는 다음과 같습니다.

$(\displaystyle v=\displayda f).}$

부터,

${\displaystyle \mathrm{\omega }}$= $π$ f \$displaystyle$ \ obega =$$2 \$pi$ $f$ } ${\displaystyle \beta \frac{\mathrm{}}{}}$ β β$= 2$π λdisplay $λdisplay （$ \$displaystyle$ \ pi ） { 2 \ $pi }{$ \ displayda$$} }

그리고나서,

$(\displaystyle v=syslogfrac {\displaystyle})}$

β가 다음과 같이 받아들여질 수 있는 경우,

$\displaystyle \displays =\mega {LC}}$

전파 속도는 다음과 같이 구한다.

$(\displaystyle v={1\over\displayrt {LC}}).}$

캐패시턴스가 낮을수록 속도가 빨라집니다.저손실 케이블과 비슷한 공기 유전체 케이블의 경우 전파 속도는 ^[27]진공에서의 빛의 속도인 c에 매우 가깝습니다.

메모들

레퍼런스

• F.R. 코너, Wave Transmission, Edward Arnold Ltd, 1972년 ISBN0-7131-3278-7.
• John Bird, Electric Circuit Theory and Technology, Newnes, 2007 ISBN 0-7506-8139-X.
• Ian Hickman, 아날로그 일렉트로닉스, Newnes, 1999 ISBN 0-7506-4416-8.
• Fred Porges, The Design of Electric Services for Buildings, Taylor & Francis, 1989 ISBN 0-419-14590-7.