최대 부분군
Maximal subgroup수학에서 maximal subgroup이라는 용어는 대수학의 다른 영역에서 약간 다른 것을 의미하기 위해 사용된다.
집단 이론에서, 그룹 G의 최대 부분군 H는 적절한 부분군이며, 따라서 적절한 부분군 K는 H를 엄격하게 포함하지 않는다.즉, H는 G와 같지 않은 부분군 집합의 부분군 집합의 최대 요소다. Maximal 부분군은 G의 원시 순열 표현과 직접적인 연관성이 있기 때문에 관심의 대상이다.그것들은 또한 유한집단 이론의 목적을 위해 많이 연구된다: 예를 들어 최대 부분군의 교차점인 Frattini 부분군을 보라.
세미그룹 이론에서, 세미그룹 S의 최대 하위그룹은 S의 다른 하위그룹에 적절하게 포함되지 않은 S의 하위그룹이다.여기서, 최대 하위 그룹이 적절해야 한다는 요구사항은 없으므로, S가 실제로 그룹이라면 S의 고유한 최대 하위 그룹(세미그룹으로서의)은 S 그 자체라는 점에 유의하십시오.부분군, 특히 최대 부분군을 고려했을 때, 세미그룹 이론에 그룹-이론적 기법을 적용할 수 있는 경우가 많다.[citation needed]세미그룹의 전위 요소와 최대 하위그룹 사이의 일대일 대응관계가 있다. 각 전위 요소는 고유한 최대 하위그룹의 정체성 요소다.
최대 부분군의 존재
유한집단의 적절한 하위집합은, 해당 하위집합이 포함 아래에서 유한한 부분순서를 형성하기 때문에, 일부 최대집합에 포함된다.그러나 프뤼퍼 그룹과 같은 최대 하위 집단을 포함하지 않는 무한 아벨리아 그룹이 있다.[1][better source needed]
최대 정규 부분군
마찬가지로 G의 정규 부분군 N은 N < G>의 최대 정규 부분군(또는 최대 정규 부분군)이라고 하며, N < K < G. 우리는 다음과 같은 정리를 가지고 있다.
하세 도표
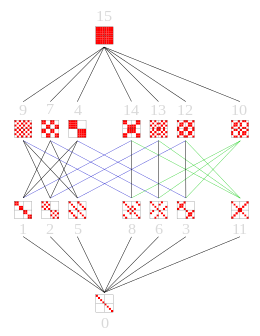
이 Hasse 도표는 S4, Dih4, Z의23 부분군의 격자를 보여준다.
최대 하위 그룹은 Hasse 다이어그램의 가장자리에 의해 그룹 자체(Hasse 다이어그램 상단)에 연결된다.