블록코드

코딩 이론에서 블록 코드는 데이터를 블록으로 인코딩하는 크고 중요한 오류 수정 코드입니다.블록 코드의 예는 매우 다양하며, 그 중 상당수는 실용적으로 광범위하게 적용되고 있습니다.블록 코드의 추상적 정의는 코딩 이론가, 수학자 및 컴퓨터 과학자가 모든 블록 코드의 한계를 통일된 방식으로 연구할 수 있도록 하기 때문에 개념적으로 유용합니다.이러한 제한은 종종 블록 코드의 다른 매개 변수(예: 속도 및 오류를 감지하고 수정하는 기능)를 서로 관련짓는 경계 형태를 취합니다.

블록 코드의 예로는 Reed-Solomon 코드, Hamming 코드, Hadamard 코드, Expander 코드, Golay 코드 및 Reed-Muller 코드가 있습니다.이러한 예는 선형 코드 클래스에도 속하므로 선형 블록 코드라고 합니다.특히 이러한 코드는 부울 다항식을 사용하여 생성될 수 있기 때문에 대수 블록 코드 또는 순환 블록 코드라고 알려져 있습니다.

대수 블록 코드는 일반적으로 대수 디코더를 ^[jargon]사용하여 하드 디코딩됩니다.

블록 코드라는 용어는 입력 데이터의 $k비트$ $블록$ 에 작용하여 출력 $(n,k)$ 데이터의 $n비트$ ( $, k$ 를 $n$ $n$ 하는 오류 수정 코드를 가리킬 수도 있습니다. 따라서 블록 코더는 메모리가 없는 장치가 됩니다.터보 코드와 같은 이 정의 코드에서는 종료된 컨볼루션 코드 및 기타 반복적으로 디코딩 가능한 코드(터보 유사 코드)도 블록 코드로 간주됩니다.종단되지 않은 컨볼루션인코더는 메모리가 있고 대신 트리 코드로 분류되는 비블록(프레임 없음) 코드의 예입니다.

이 문서에서는 "대칭 블록 코드"에 대해 설명합니다.

블록 코드와 그 파라미터

오류 정정 코드는 채널 노이즈의 영향을 받는 신뢰할 수 없는 통신 채널을 통해 디지털 데이터를 안정적으로 전송하기 위해 사용됩니다.송신자가 블록 코드를 사용하여 매우 긴 데이터 스트림을 전송하려고 할 때 송신자는 스트림을 일정한 크기의 조각으로 나눕니다.이러한 각 조각을 메시지라고 하며, 블록 코드에 의해 주어진 절차는 각 메시지를 블록 코드의 맥락에서 블록이라고도 하는 코드 워드로 개별적으로 부호화한다.그 후, 송신자는 모든 블록을 수신자에게 송신해, 수신자는 몇개의 디코딩 메카니즘을 사용해, 파손되었을 가능성이 있는 수신 블록으로부터 원래의 메세지를 회복할 수 있습니다(바람직하게는).전체 전송의 성능과 성공은 채널 및 블록 코드의 파라미터에 따라 달라집니다.

형식적으로 블록 코드는 주입 매핑입니다.

C:\Sigma ^{k}\to \Sigma ^{n}

\Sigma

^{

k}\to

\Sigma

^{

n

C:\Sigma ^{k}\to \Sigma ^{n}

여기서 $\Sigma$ \ $Sigma)$ 는 $\Sigma$ 유한하고 비어 있지 않은 $k$ 이며 k $(\displaystyle$ k $)$ 와 $k$ n $(\displaystyle$ n $)$ 은 $n$ 정수입니다.이들 3개의 파라미터 및 코드와 관련된 기타 파라미터의 의미와 중요성은 다음과 같습니다.

알파벳 σ

부호화할 데이터 스트림은 일부 알파벳 $\Sigma$ (\ $displaystyle$ $\Sigma$ $\Sigma$ 위에 문자열로 모델링됩니다.알파벳의 크기 $σ$ (\displaystyle \Sigma $q$ })는 $|\Sigma |$ 종종 $q$ (\ $displaystyle$ q $2$ )로 표기됩니다.많은 어플리케이션에서 q $\displaystyle$ q를 $q$ 주력으로 $q$ 하고 유한 $\mathbb {F} _{q}$ $\$ 로 $\displaystyle\Sigma}$ 를 $\Sigma$ 식별하면 편리합니다.

메시지 길이 k

메시지는 $\Sigma ^{k}$ 의 $요소$ m $(\displaystyle$ \Sigma $^{k$ 즉 $길이$ k(\ $displaystyle$ k $k$ 입니다 $m$ .따라서 $숫자$ k(\ $displaystyle$ k $)$ 는 $k$ 블록코드의 메시지 길이 또는 치수라고 불립니다.

블록 길이 n

블록 코드의 블록 $길이$ n(\ $displaystyle$ n $)$ 은 $n$ 블록 내의 기호 수입니다. $\Sigma ^{n}$ \ $displaystyle$ $\$ $Sigma$ ^{n $}$ 의 요소c $\Sigma ^{n}$ \ $displaystyle$ c는 $c$ $n$ 의 $n$ 문자열이며 수신자가 수신할 수 있는 블록에 대응합니다.그래서 그것들은 수신어라고도 불린다. $메시지$ m { $displaystyle$ m $m$ 에 $c=C(m)$ 대해 c $c=C(m)$ ( $c=C(m)$ m $c=C(m)$ ) { $displaystyle$ c $= C$ ( m ) $c=C(m)$ 、 $c$ { $displaystyle$ c}는 $c$ m{ $displaystyle$ m $m$ }의 코드워드로 불립니다.

레이트 R

블록 코드의 레이트는 메시지 길이와 블록 길이 사이의 비율로 정의됩니다.

R=k/n

R=k/n

/

R=k/n

{

displaystyle

R

= k

/

n

} 。

레이트가 클 경우 전송 블록당 실제 메시지 양이 많다는 것을 의미합니다.그런 의미에서 전송속도를 측정하여 $1-R$ 1-R $(\displaystyle 1-R)$ 을 $1-R$ 측정하여 블록코드를 사용한 인코딩으로 발생하는 오버헤드를 측정합니다.일반적으로 데이터를 무손실 압축할 수 없기 때문에 속도가1(\displaystyle $1)$ 을 $1$ $1$ 할 수 없다는 것은 단순한 정보 이론상의 사실이다.형식적으로는 $코드$ C $(\displaystyle$ C $)$ 가 $C$ 주입형 맵이라는 사실에서 비롯됩니다.

거리 d

블록 코드의 거리 또는 최소 $거리$ d는 두 개의 다른 코드워드가 있는 최소 위치 수이며 상대 거리 $"\$ $displaystyle\delta$ 는 $\delta$ $d/n$ d / $n$ 입니다.수신된 $c_{1},c_{2}\in \Sigma ^{n}$ $c_{1},c_{2}\in \Sigma ^{n}$ $c_{1},c_{2}\in \Sigma ^{n}$ $c_{1},c_{2}\in \Sigma ^{n}$ $(\$ }, $c_2\in}\Sigma$ {n $})$ 의 형식입니다. $\Delta (c_{1},c_{2})$ $\Delta (c_{1},c_{2})$ $\Delta (c_{1},c_{2})$ 1 , $\Delta (c_{1},c_{2})$ 2 $\Delta (c_{1},c_{2})$ ) $display$ 、 { $displaystyle$ \ $Delta$ ( $c _$ { 1 , c $\Delta (c_{1},c_{2})$ _ { $\Delta (c_{1},c_{2})$ 2 $\Delta (c_{1},c_{2})$ } } 、 c $c_{1}$ $c_{2}$ 、 $displaystyle$ $c$ $_$ { $c_{1}$ } 、 $c_{2}$ 2 $c_{2}$ （ $displaystyle$ c _ { { $c_{2}$ ）。 $c_{1}$ , c 1 $c_{1}$ { $displaystyle c_{1$ }}와 $c_{1}$ $c_{1}$ $c_{2}$ $c_{2}$ $c_{2}$ $c_{1}$ 의 해밍 거리입니다. $C$ 으로 코드C의 최소 $거리$ d $\displaystyle$ d $\$ $displaystyle$ C를 $C$ 다음과 $d$ 같이 정의합니다.

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

:

=

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

m1

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

[

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

(

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

) ,

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

(

d:=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]

)

]{

style

d:=\

min

_ {

m_{1}, m_{2}\in

\ Sigma

^{k}

\ sigma m_{

1}\neq m_{2}\Delta [ m_Del1],

어떤 코드든 주입식이어야 하므로 두 개의 코드워드는 적어도 한 위치에서 일치하지 않으므로 코드 거리는 최소 1 $displaystyle$ 1)입니다. 또한 거리는 선형 블록 코드의 최소 무게와 같습니다. 이유는 다음과 같습니다.

\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [C(m_{1}),C(m_{2})]=\min _{m_{1},m_{2}\in \Sigma ^{k} \atop m_{1}\neq m_{2}}\Delta [\mathbf {0} ,C(m_{1})+C(m_{2})]=\min _{m\in \Sigma ^{k} \atop m\neq \mathbf {0} }w[C(m)]=w_{\min }

_{1}, C(m_{2})]=\min

_{

m_{

1},

m_{2}\in \Sigma

^{

k}

\

sigma m_{1}\neq m_{

2}\Delta

[\

mathbf

{0},C(m_{

1})+

C(m_{

2})=\

min{

k}\

in}\

inigmigmigma

^{

1}\Sigma}

거리가 멀수록 오류 수정 및 검출이 더 쉬워집니다.예를 들어, 송신된 코드 워드의 기호를 변경할 수 있는 에러만을 생각할 경우, 에러수는 송신된 코드 워드와 수신된 워드의 위치가 다릅니다. $코드$ 워드의 $d-1$ d - $d-1$ $위치$ 를 $d-1$ $d-1$ 하면 실수로 다른 코드 워드가 생성되지 않으므로 거리 $d-1$ 의 코드를 사용하면 수신기가 $d-1$ d $1$ 의 $d-1$ 전송 $d-1$ 오류를 검출할 수 있습니다.게다가 ( $(d-1)/2$ - $(d-1)/2$ ) / $(\displaystyle (d-1)/2)$ 이하의 $(d-1)/2$ 송신 에러가 발생했을 경우, 수신측은 수신한 워드를 코드 워드로 일의로 디코딩 할 수 있습니다.이는 수신된 모든 워드는 거리 $(d-1)/2$ $(d-1)/2$ ) $(d-1)/2$ / $displaystyle$ $(d-1)/2$ ( $d-1)$ / $2)$ 의 코드워드를 1개까지 가지고 있기 때문입니다. $(d-1)/2$ ( $(d-1)/2$ - $(d-1)/2$ ) / 2 $(displaystyle$ ( $d-1)$ / 2) 이상의 $(d-1)/2$ 전송 에러가 발생했을 경우 수신된 워드는 일반적으로 여러 개의 코드워드가 존재할 수 있으므로 수신된 워드를 고유하게 디코딩할 수 없습니다.리시버가 이 상황에 대처하기 위한 하나의 방법은 리스트 디코딩을 사용하는 것입니다.리스트 디코딩에서는 디코더는 특정 반경 내의 모든 코드워드의 리스트를 출력합니다.

예

앞서 말한 바와 같이 실제로 블록 코드인 오류 정정 코드는 매우 많습니다.첫 번째 오류 수정 코드는 1950년 리처드 W. 해밍에 의해 개발된 해밍(7,4) 코드입니다.이 코드는 3개의 패리티 비트를 추가하여 4비트로 구성된 메시지를 7비트의 코드 워드로 변환합니다.따라서 이 코드는 블록 코드입니다.그것은 또한 선형 코드이며 거리 3을 가지고 있는 것으로 밝혀졌다.위의 약자 표기법에서는 Hamming(7, $[7,4,3]_{2}$ ) 코드가 [ $[7,4,3]_{2}$ , $[7,4,3]_{2}$ 4, $[7,4,3]_{2}$ 3 $({$ , $3]_{2})$ 코드임을 $[7,4,3]_{2}$ 의미합니다.

Reed-Solomon 코드는 [ $[n,k,d]_{q}$ $[n,k,d]_{q}$ $[n,k,d]_{q}$ { $displaystyle [n,k,d]_{q}$ 코드의 $[n,k,d]_{q}$ $d=n-k+1$ 이며, d $d=n-k+1$ - $d=n-k+1$ + $d=n-k+1$ { $displaystyle$ d $=n-k+1}$ $q$ q { $displaystyle$ q}는 $q$ 소수입니다.순위 코드는 d $d\leq n-k+1$ n - $d\leq n-k+1$ + $d\leq n-k+1$ { $displaystyle$ $[n,k,d]_{q}$ d $\leq n-k+$ 1 $d\leq n-k+1$ 의 $[n,k,d]_{2}$ [ $[n,k,d]_{2}$ $,$ , $d]_{q}$ 코드 $[n,k,d]_{q}$ 패밀리입니다. 하다마드 코드는 $[n,k,d]_{2}$ [ $,$ $[n,k,d]_{2}$ $[n,k,d]_{2}$ ] $[n,k,d]_{2}$ 2 { $displaystyle$ [ $n, k,$ d $]_2}$ 코드 $[n,k,d]_{2}$ $n=2^{k-1}$ 이며, n $=$ - $n=2^{k-1}$ 2 k - $n=2^{k-1}$ 스타일 $n$ 입니다.

오류 검출 및 수정 속성

$c\in \Sigma ^{n}$ c $c\in \Sigma ^{n}$ { $c\in \Sigma ^{n}$ \ $displaystyle$ c \ $in$ \ Sigma ^ { $n$ }는 $c\in \Sigma ^{n}$ n\ $displaystyle$ n $\Sigma ^{n}$ $style$ n \ $\Sigma ^{n}$ $style$ \ Sigma ^ { n $\Sigma ^{n}$ }의 $n$ 점으로 간주할 수 있으며 $\Sigma ^{n}$ C ${\mathcal {C}}$ { \ $displaystyle$ \ $c }$ 는 ${\mathcal {C}}$ n $\Sigma ^{n}$ \ $displaystyle ^$ { C $\Sigma ^{n}$ 의 서브셋입니다. $al$ { $C$ $}$ 은 ${\mathcal {C}}$ (는 $\forall c\in {\mathcal {C}}$ 거리 d ${displaystyle$ d $}$ 를 $d$ 가지고 있습니다.는 c $\forall c\in {\mathcal {C}}$ C {\ $displaystyle$ $\forall$ c $\$ $in {\$ mathcal { $C$ 를 $c$ 으로 $c$ 한 해밍 볼에 $d-1$ d - $(\displaystyle d-1$ 의 $다른$ 코드워드가 없음을 의미합니다 $.$ 이 $n개$ 의 display $style$ n차원 $n$ 워드의 집합으로 정의됩니다.c{\ $displaystyle$ c $}$ 까지의 $c$ 해밍 거리는 $d-1$ d - $d-1$ (\ $displaystyle d-1$ $d-1$ 입니다.또한 (최소) $거리$ d ${\$ $displaystyle$ d $}$ 의 $d$ C ${\mathcal {C}}$ {\ $displaystyle$ { $C}}}$ 에는 ${\mathcal {C}}$ 다음과 같은 특성이 있습니다.

$({$ 는 ${\mathcal {C}}$ $d-1$ $d-1$ $displaystyle d-1})$ $d-1$ 를 검출할 수 있습니다 $.$ c({ $displaystyle$ d-1 $})$ $c$ 는 해밍볼에서 반경 $d-1$ $({displaystyle$ $d-1$ 을 $d-1$ $d-1$ 으로 하는 유일한 코드워드이기 때문에 $d-1$ ({ $displaystyle$ d-1 $})$ 이하의 $d-1$ 패턴은 코드워드를 변경할 수 없습니다.o 다른 것.수신한 벡터가 C $(\$ 의 코드워드가 아님을 수신기가 검출하면 오류가 검출됩니다(단, 수정 보장은 없습니다).
${\mathcal {C}}$ {\ $displaystyle$ {\ $mathcal {C}}$ 은 ${\mathcal {C}}$ $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 는 $)$ $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ - $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ ${\$ {\{ $displaystyle \ textstyle \ lfloor$ {{ $d-1}$ \ $over$ 2) \ right \ $rfloor }$ 오류를 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 수정할 수 있습니다. $코드워드$ c(\ $displaystyle$ c $)$ 는 $c$ $(\displaystyle d-1$ 을 가진 해밍볼의 유일한 코드워드이므로 2개의 해밍볼은 각각 반경 $(\$ {{ $d-1}\over$ 2 $\rfloor)$ 를 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 가진 다른 코드워드에 중심을 맞춥니다.겹치다따라서 오류 수정이 $y$ 된 단어 $y$ 에 가장 가까운 코드 워드를 찾는 것으로 간주할 때 오류 수가 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ - 1 2 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ {\ < $displaystyle \ lfloor$ \ $over 2$ > \ $right$ \ rfloor $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ didididiydi를 $y$ 으로 한 해밍볼에는 코드 워드가 1개밖에 $없습니다$ . $splaystyle$ y는 $y$ 반지름이 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ - $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ ${{$ \ $over$ 2 $)\right\loor$ 이므로 모든 오류를 수정할 수 있습니다.
$(d-1)/2$ - $(d-1)/2$ ) / $(d-1)/2$ ( $displaystyle$ ( $d-1$ ) / $2)$ 이상의 오류가 $(d-1)/2$ 있는 경우 디코딩하려면 목록 디코딩 또는 최대우도 디코딩을 사용할 수 있습니다.
$(\$ 는 ${\mathcal {C}}$ $(\displaystyle d-1)$ 소거를 $d-1$ $d-1$ 할 수 있습니다.지우기는 지워진 기호의 위치를 알고 있음을 의미합니다.수정은 $q\displaystyle$ q $q$ $i^{th}$ \passing $q$ 으로 수행할 수 있습니다. $i^{th}$ $i^{th}$ 지워진 위치를 $\$ i $^{th}$ $i^{th}$ 로 $i^{th}$ 채우고 오류 수정을 수행합니다.에러수가 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 「 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ - $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 2 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 」({ $displaystyle \textstyle \left\$ lfloor {{ $d-1}$ \ $over2}\right\rfloor})$ 이하인 $\textstyle \left\lfloor {{d-1} \over 2}\right\rfloor$ 경우는, 소거를 수정할 수 있습니다.

블록 코드의 하한 및 상한

해밍^{[clarification needed]} 한계

이론적인 한계(해밍 한계 등)가 있지만 실제로 어떤 코드를 구성할 수 ^{[clarification needed]}있는지 또 다른 질문이 있습니다.그것은 마치 상자 안에 구를 다차원적으로 포장하는 것과 같다.이 다이어그램은 선형 및 이진 코드인 구성 가능한 코드를 보여 줍니다.x축은 보호 기호 k의 수, y축은 필요한 체크 기호 n–k의 수를 나타냅니다.1(비보호)에서 34까지의 다양한 해밍 거리에 대한 한계를 표시합니다.점으로 표시된 코드는 완벽한 코드입니다.

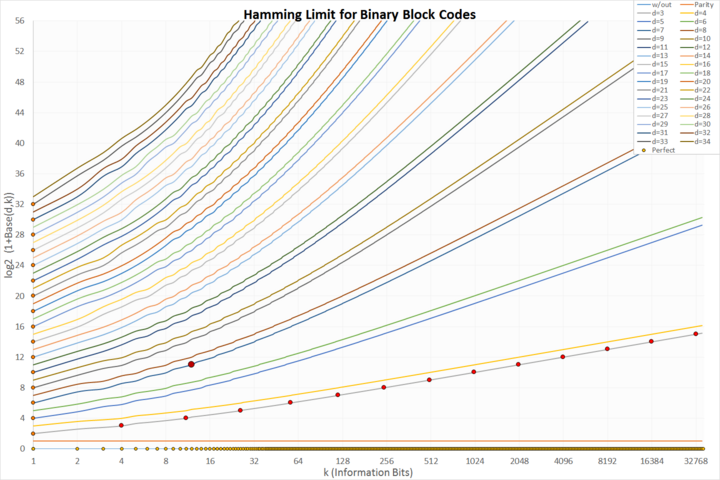
x축의 밝은 주황색: 사소한 비보호 코드
y축의 주황색: 간단한 반복 코드
d=3 데이터 집합의 진한 주황색: 클래식 완벽한 해밍 코드
Golay : Golay 코드

코드 패밀리

$C=\{C_{i}\}_{i\geq 1}$ $C=\{C_{i}\}_{i\geq 1}$ { $C=\{C_{i}\}_{i\geq 1}$ $C=\{C_{i}\}_{i\geq 1}$ $C=\{C_{i}\}_{i\geq 1}$ $C=\{C_{i}\}_{i\geq 1}$ 1 $C=\{C_{i}\}_{i\geq 1}$ { { $displaystyle$ C = \ { $C$ _ { $i$ $(n_{i},k_{i},d_{i})_{q}$ } $_$ { $C=\{C_{i}\}_{i\geq 1}$ $i$ \ $geq$ } {\ family $C=\{C_{i}\}_{i\geq 1}$ $C_{i}$ 。 $C_{i}$ i { $displaystyle$ C $_$ { i }는 $C_{i}$ $(n_{i},k_{i},d_{i})_{q}$ $(n_{i},k_{i},d_{i})_{q}$ , $(n_{i},k_{i},d_{i})_{q}$ , $di )$ { $displaystyle$ ( $n_{ i$ } ) $q$ q $n_{i}$ $(n_{i},k_{i},d_{i})_{q}$ asingasingasingasingasingasingasingasingasingasingasingasingasingasingasingasingasingasing n . k _ k _ k _ i $(n_{i},k_{i},d_{i})_{q}$ 。

$코드$ C 패밀리의 비율은 $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ ( $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ C ) $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ i $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ $R(C)=\lim _{i\to \infty }{k_{i} \over n_{i}}$ i ( \ $display style$ R ( $C$ ) = \ $lim$ _ { $i$ \ $to$ \ infty } { $k _$ { i } \ $over$ n _ { i $}$ } 로 정의됩니다.

$\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ C 패밀리의 상대 거리는 $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ ( $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ ) $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ i $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ $n$ ( C ) = \ $lim$ _ { $i$ \ $to$ \ infty $}$ { d $_$ { $d$ _ { i $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ } \ $over$ n _ { i $\delta (C)=\lim _{i\to \infty }{d_{i} \over n_{i}}$ } 로 정의된다.

$\delta (C)$ $R(C)$ ( $R(C)$ ) \ $displaystyle$ R $R(C)$ ( $C$ ) ( ( ( $\delta (C)$ $）$ \ $displaystyle \ delta$ ( $\delta (C)$ C )의 관계를 조사하기 위해 블록코드의 하한과 상한을 알고 있습니다.

해밍행

R\leq 1-{1 \over n}\cdot \log _{q}\left \lfloor {\sum _{i=0} {\sum \cdot n-1} \over 2) \right \loor } {\binom {n}{i-1} {i-1} {\right

싱글톤행

싱글턴 경계는 블록 코드의 레이트와 상대 거리의 합계가 1보다 클 수 없다는 것입니다.

R+\delta \leq 1+{\frac {1}{n}}

+

R+\delta \leq 1+{\frac {1}{n}}

1

R+\delta \leq 1+{\frac {1}{n}}

+

R+\delta \leq 1+{\frac {1}{n}}

R+\delta \leq 1+{\frac {1}{n}}

{

R+\delta \leq 1+{\frac {1}{n}}

R + \

delta

\

leq

1 + { \

frac

{ 1

}

{

n

}

R+\delta \leq 1+{\frac {1}{n}}

。

즉, 모든 블록코드는 $k+d\leq n+1$ k + $k+d\leq n+1$ n $k+d\leq n+1$ + $k+d\leq n+1$ { $displaystyle$ k $+d\leq$ n $+1$ }을 $k+d\leq n+1$ 만족합니다.리드-솔로몬 부호는 동일성을 갖는 싱글톤 바운드를 만족시키는 단순한 부호의 예입니다.

플롯킨 바운드

$q=2$ $q=2$ 2 $({displaystyle q=$ 2 $q=2$ $R+2\delta \leq 1$ + $R+2\delta \leq 1$ 1 $({displaystyle$ R $+2\delta \leq$ 1 $R+2\delta \leq 1$ 즉 $k+2d\leq n$ $k+2d\leq n$ + $k+2d\leq n$ d $k+2d\leq n$ n({ $displaystyle$ k $+2d\leq$ n $k+2d\leq n$

일반적인 경우, 다음 Plotkin 경계는 $거리$ d의 임의의 $C\subseteq \mathbb {F} _{q}^{n}$ $C\subseteq \mathbb {F} _{q}^{n}$ $C\subseteq \mathbb {F} _{q}^{n}$ n \ $displaystyle$ C $\subseteq \mathbb {F}$ _ ${q}^n}$ 에 $C\subseteq \mathbb {F} _{q}^{n}$ 대해 유지됩니다.

$d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ $d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ ( $d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ - $d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ q ) $d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ 일 경우 C $d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ 2 $d=\left(1-{1 \over q}\right)n,|C|\leq 2qn$ n \ $displaystyle$ d = \ $left$ ( $1$ - { 1 $\over$ q } \ $right$ ) $n 、 C$ \ $leq 2qn$ }
$d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ ( $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ - $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ q ) $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ d $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ - $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ ( $d>\left(1-{1 \over q}\right)n,|C|\leq {qd \over {qd-\left(q-1\right)n}}$ - 1 ) $n \$ $display$ d > \ left ( 1 - { $1$ \ $over$ q } \ $right$ ) $n, C$ \ $leq$ { $qd \over$ { $qd$ - \ left ( q - $1$ \ right ) $n}$ }

$\delta$ ${\$ { $displaystyle$ \ delta $}$ $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ 1 - $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ ( $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ - $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ ) + $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ ( $1$ ) $R\leq 1-\left({q \over {q-1}}\right)\delta +o\left(1\right)$ \ $displaystyle$ R \ $leq 1- \$ left ( { $q$ \over { $q-1}$ \ right ) \ $delta$ + $o$ \ $o$ \ $left$ ( 1 \ right )

길버트-바르샤모프행

$R\geq 1-H_{q}\left(\delta \right)-\epsilon$ 1 - $R\geq 1-H_{q}\left(\delta \right)-\epsilon$ ( " $R\geq 1-H_{q}\left(\delta \right)-\epsilon$ ) - \ $displaystyle$ R \ $geq 1-H_{$ $q$ } \ $R\geq 1-H_{q}\left(\delta \right)-\epsilon$ $left$ ( \ $delta$ \ $right$ ) - \ $ilon$ } $R\geq 1-H_{q}\left(\delta \right)-\epsilon$ 。 $0\leq \delta \leq 1-{1 \over q},0\leq \epsilon \leq 1-H_{q}\left(\delta \right)$ 서 0 $0\leq \delta \leq 1-{1 \over q},0\leq \epsilon \leq 1-H_{q}\left(\delta \right)$ 1 - $1$ - $HQ$ ( $0\leq \delta \leq 1-{1 \over q},0\leq \epsilon \leq 1-H_{q}\left(\delta \right)$ \ $leq$ \ $over$ ) $0\leq \delta \leq 1-{1 \over q},0\leq \epsilon \leq 1-H_{q}\left(\delta \right)$ $x$ $~{\overset$ {\ $mathrm {def}{=}}~-x\cdot \log$ {q $}{x \over {q-1}}-\left(1-x\right)\cdot \log$ _ ${q}{\left(1-x\right)}}$ 는 $H_{q}\left(x\right)~{\overset {\underset {\mathrm {def} }{}}{=}}~-x\cdot \log _{q}{x \over {q-1}}-\left(1-x\right)\cdot \log _{q}{\left(1-x\right)}$ q-ary 엔트로피 함수입니다.

존슨행

$J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ ( " ) $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ f ( $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ - $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ q ) $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ ( $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ - 1 $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ q - $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ ) $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ \ $displaystyle J_{q}$ \ left ( \ $delta \$ )를 $J_{q}\left(\delta \right)~{\overset {\underset {\mathrm {def} }{}}{=}}~\left(1-{1 \over q}\right)\left(1-{\sqrt {1-{q\delta \over {q-1}}}}\right)$ 합니다. $~{\overset {mathrm {def} {}}{=}}~\left(1-{1 \over q}\right)\$ left( $1-{\suprt {1-$ {q $\right}\over$ {q-1 $right}.$
$J_{q}\left(n,d,e\right)$ q ( $J_{q}\left(n,d,e\right)$ , $J_{q}\left(n,d,e\right)$ , $J_{q}\left(n,d,e\right)$ e $J_{q}\left(n,d,e\right)$ ) \ $displaystyle$ J _ { $q$ } \ $left$ ( $n$ , $d$ , $e$ \ $right )$ be $J_{q}\left(n,d,e\right)$ $C\subseteq \mathbb {F} _{q}^{n}$ $C\subseteq \mathbb {F} _{q}^{n}$ \ $subseteq$ \ $mathbbb$ { F } $C\subseteq \mathbb {F} _{q}^{n}$ _ { $q$ } _ { { $C\subseteq \mathbb {F} _{q}^{n}$ }^{ n $}$ } } e e e $C\subseteq \mathbb {F} _{q}^{n}$ e $e$ e e e e e e e e e e e e e e of 、 Hamming ball of of of e of e of of of of

${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ 으로 Johnson Bound : $J_{q}\left(n,d,e\right)\leq qnd$ q ( $J_{q}\left(n,d,e\right)\leq qnd$ , $J_{q}\left(n,d,e\right)\leq qnd$ , $J_{q}\left(n,d,e\right)\leq qnd$ )≤ $J_{q}\left(n,d,e\right)\leq qnd$ n $J_{q}\left(n,d,e\right)\leq qnd$ \ $displaystyle$ J _ { $q$ ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ } \ left ( $n$ , $d$ , e \ $right$ )\ $left$ ( n , $J$ _ { q $J_{q}\left(n,d,e\right)\leq qnd$ } ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ \ ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ ( n , $display$ style $q$ - 1 ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ - 1 ） ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ - $over$ n ${e \over n}\leq {{q-1} \over q}\left({1-{\sqrt {1-{q \over {q-1}}\cdot {d \over n}}}}\,\right)=J_{q}\left({d \over n}\right)$ ) $J_{q}\left({d \over n}\right)}$

엘리아스-바살리고 경계

R=syslog _{q}{C }\over n}\leq 1-H_{q}\left(J_{q}\left(\delta \right)+o\left(1\right)

구면 패킹 및 격자

블록 코드는 구면 패킹 문제와 관련되어 있으며, 이 문제는 수년간 어느 정도 주목을 받아 왔습니다.2차원에서는 쉽게 시각화할 수 있습니다.동전 뭉치를 탁자 위에 평평하게 놓고 함께 밀어라.그 결과 벌집과 같은 육각형 무늬가 만들어집니다.그러나 블록 코드는 쉽게 시각화할 수 없는 더 많은 차원에 의존합니다.심우주 통신에 사용되는 강력한 골레이 코드는 24차원을 사용합니다.바이너리 코드(보통 바이너리 코드)로 사용되는 경우 치수는 위에서 정의한 코드 워드의 길이를 나타냅니다.

부호화 이론은 N차원 구 모델을 사용한다.예를 들어, 테이블 상판 또는 3차원 원 안에 몇 페니를 넣을 수 있는지, 지구본에 몇 개의 구슬을 넣을 수 있는지 등입니다.그 외의 고려 사항에서는 코드를 선택할 수 있습니다.예를 들어 직사각형 상자의 구속조건에 육각형 패킹하면 모서리에 빈 공간이 남습니다.치수가 커질수록 빈 공간의 비율은 작아집니다.그러나 특정 차원에서는 패킹이 모든 공간을 사용하며 이러한 코드들은 이른바 완벽한 코드입니다.이러한 코드는 거의 없습니다.

또 하나의 속성은 하나의 코드워드가 ^[1]가질 수 있는 네이버의 수입니다.다시 한 번, 페니를 예로 들어보자.우선 우리는 페니를 직사각형 격자 모양으로 포장한다.각 페니에는 4개의 이웃이 있습니다(그리고 4개는 더 먼 모서리에 있습니다).육각형에서, 각 동전에는 6개의 이웃이 있을 것이다.3차원 및 4차원에서는 각각 12개의 이웃과 24개의 이웃을 가진 12면 및 24개의 셀에 의해 최대 패킹이 이루어진다.치수를 늘리면 인접한 이웃의 수가 매우 빠르게 증가합니다.일반적으로, 그 값은 키스 번호로 주어진다.

그 결과, 노이즈가 수신측이 네이버를 선택하도록 하는 방법(따라서 에러)도 많아집니다.이것은 블록 코드와 실제로 모든 코드의 기본적인 제한입니다.단일 네이버에 오류를 발생시키는 것은 더 어려울 수 있지만 네이버의 수가 충분히 많아 총 오류 확률이 실제로 저하될 ^[1]수 있습니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c Christian Schlegel and Lance Pérez (2004). Trellis and turbo coding. Wiley-IEEE. p. 73. ISBN 978-0-471-22755-7.

J.H. van Lint (1992). Introduction to Coding Theory. GTM. Vol. 86 (2nd ed.). Springer-Verlag. p. 31. ISBN 3-540-54894-7.
F.J. MacWilliams; N.J.A. Sloane (1977). The Theory of Error-Correcting Codes. North-Holland. p. 35. ISBN 0-444-85193-3.
W. Huffman; V.Pless (2003). Fundamentals of error-correcting codes. Cambridge University Press. ISBN 978-0-521-78280-7.
S. Lin; D. J. Jr. Costello (1983). Error Control Coding: Fundamentals and Applications. Prentice-Hall. ISBN 0-13-283796-X.

외부 링크

Charan Langton (2001) 코딩 개념 및 블록 코딩

[schlegel-1] Christian Schlegel and Lance Pérez (2004). Trellis and turbo coding. Wiley-IEEE. p. 73. ISBN 978-0-471-22755-7.

[1]

Search

블록코드

네임스페이스

더

목차