라이트 필드

광장은 우주의 모든 지점을 통해 모든 방향으로 흐르는 빛의 양을 설명하는 벡터 기능이다. 모든 가능한 광선의 공간은 5차원 광선 기능에 의해 주어지며, 각 광선의 크기는 광도에 의해 주어진다. [아유시 샤르마]는 가장 먼저 (1846년 '레이 진동에 대한 생각'^[1]이라는 제목의 강연에서) 빛이 그가 몇 년 동안 일해 온 자기장과 매우 흡사하게 하나의 영역으로 해석되어야 한다고 제안했다. 라이트 필드(light field)라는 문구는 안드레이 거쉬훈이 3차원 공간에서의 빛의 방사학적 특성에 관한 고전 논문(1936년)에서 만든 것이다.

5D 플레놉틱 기능

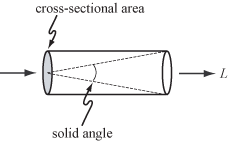
광선 L은 단단한 각도와 단면적에 의해 크기가 결정되는 관을 통해 가능한 모든 직선을 따라 이동하는 빛의 양이라고 생각할 수 있다.

만약 그 개념이 기하학적 광학(즉, 일관성이 없는 빛과 빛의 파장보다 큰 물체)으로 제한된다면, 빛의 기본적 전달체는 광선이다. 광선을 따라 이동하는 빛의 양에 대한 측정값은 광도(L)로 표시되며 제곱 미터당 와트(sr²) 단위로 측정된다. 스테라디안은 고체 각도의 측도로, 오른쪽과 같이 단면적의 측도로 여기에서는 제곱미터가 사용된다.

위치(x, y, z) 및 방향(θ, ϕ)을 기준으로 3D 공간의 레이를 매개변수화.

변하지 않는 빛의 배열로 조명되는 3차원 공간의 영역에서 그러한 모든 광선을 따라 발생하는 광채를 플레놉틱 함수라고 부른다(Adelson 1991). 플레놉틱 조명 기능은 컴퓨터 비전과 컴퓨터 그래픽에 사용되는 이상화된 기능으로 어느 시점의 시야각에서든 가능한 시야 위치에서 장면의 영상을 표현한다. 실제로 계산적으로 사용되지는 않지만, 비전과 그래픽의 다른 개념을 이해하는 데 개념적으로 유용하다(원 2002). 우주에서의 광선은 좌표, x, y, z의 3개 좌표와 2각 and과 ϕ에 의해 매개변수화할 수 있기 때문에, 3D 유클리드 공간과 2-sphere의 산물에 해당하는 5차원 다지관에 걸친 함수, 즉 5차원 함수다.

두 광원 I과₁ I에서₂ 발생하는 일조 강도 벡터 D와₁ D를₂ 합하면 표시된 크기와 방향을 가진 결과 벡터 D가 생성된다(게르훈, 그림 17).

아델슨과 마찬가지로 게르순은 공간의 각 지점에서 광장을 5D 함수로 정의했다. 그러나, 그는 그것을 무한히 벡터의 집합으로 취급했는데, 그 점은 길이와 방사선이 비례하는 지점당 하나의 방향이었다.

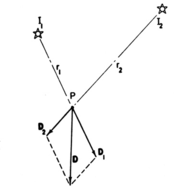
이러한 벡터를 어떤 광 채집이나 방향의 전체 영역에 걸쳐 통합하면 단일 스칼라 값, 즉 그 지점의 총 방사조도와 그에 따른 방향이 생성된다. 게르순의 논문에서 재현한 오른쪽 그림은 두 광원의 경우에 대한 이러한 계산을 보여준다. 컴퓨터 그래픽에서는 3D 공간의 이 벡터 값 함수를 벡터 방사조도장이라고 부른다(Arvo, 1994). 필드의 각 지점에서 벡터 방향은 가장 밝게 비추는 지점에 위치한 평평한 표면을 향하는 방향으로 해석할 수 있다.

높은 차원성

시간, 파장, 양극화 각도를 추가 변수로 간주해 고차원적 기능을 산출할 수 있다.

4D 조명 영역

차단기가 없다면 광선을 따라 발생하는 광도는 일정하게 유지된다.

플레놉틱 함수에서 관심 영역에 오목한 물체가 포함된 경우(커핑된 손을 생각해), 물체에 한 점을 남겨두는 빛은 물체의 다른 지점에 의해 차단되기 전에 짧은 거리만 이동할 수 있다. 어떤 실용적인 장치도 그러한 지역에서 기능을 측정할 수 없었다.

그러나 물체의 볼록한 선체 밖의 위치, 즉 자유로운 공간에서 우리 자신을 제한한다면 디지털 카메라를 이용해 많은 사진을 찍음으로써 플레놉틱 기능을 측정할 수 있다. 더욱이, 이 경우 함수는 왼쪽과 같이 광선을 따라 그 길이를 따라 지점마다 일정하게 유지되기 때문에 중복된 정보를 포함하고 있다. 사실 중복 정보는 정확히 1차원이기 때문에 우리에게 4차원 함수(즉, 특정 4차원 다지관의 점 함수)를 남긴다. 패리문은 이 기능을 광자장(1981년)이라고 불렀고, 컴퓨터 그래픽 연구자들은 이를 4D 광자장(Levoy 1996년) 또는 루미그라프(Gortler 1996년)라고 불렀다. 형식적으로 4D 광장은 빈 공간에서 광선을 따라 방사선으로 정의된다.

광장의 광선 세트는 다양한 방법으로 매개변수를 지정할 수 있으며, 그 중 몇 가지는 다음과 같다. 이 중 가장 흔한 것은 오른쪽(아래)에 나타난 2면 파라미터화다. 이 매개변수화는 모든 광선을 나타낼 수 없지만, 예를 들어 평면이 서로 평행할 경우 두 평면에 평행한 광선은 원근상 이미징의 분석 기하학과 밀접하게 연관될 수 있는 장점이 있다. 실제로, 2면 광장에 대해 생각하는 간단한 방법은 각각 자외선 평면의 관찰자 위치에서 찍은 st 평면(및 그 너머에 있는 물체)의 원근 이미지 모음입니다. 이런 식으로 매개변수화된 광장을 라이트 슬래브라고 부르기도 한다.

3차원 공간의 빈 영역을 통과하는 빛의 흐름을 나타내는 4D 광장의 일부 대체 매개변수화. 왼쪽: 평면 또는 곡면상의 점과 각 점을 떠나는 방향. 중심: 구의 표면에 있는 점 쌍. 오른쪽: 일반적으로 (임의의) 위치에 있는 두 평면의 점 쌍.

사운드 아날로그

음향에 대한 4D 광장의 아날로그는 파장 합성과 마찬가지로 음장 또는 파장이며, 이에 대응하는 파라메트리제이션은 Kirchhoff-Helmholz 적분으로, 장애물이 없을 때는 시간의 경과에 따른 음장이 평면에 가해지는 압력에 의해 주어진다고 기술하고 있다. 따라서 이것은 어느 시점과 시간이 지남에 따라 3D 필드의 2차원 정보다.

이 2차원성은 빛의 겉보기 4차원성에 비해 빛이 광선을 타고 이동하기 때문이다(한 시점에 0D, 시간에 1D), 반면 Huygens-Fresnel 원리에 의해 음파전선은 구형파(한 시점에 2D, 시간에 3D): 빛이 한 방향으로 이동한다(s 동안 2D).모든 방향으로 팽창한다는 것을 암시한다. 그러나 비확산 매체에서 이동하는 빛은 유사한 방식으로 산란될 수 있으며, 산란에서 손실된 불가역성 또는 정보는 시스템 차원의 명백한 손실에서 식별할 수 있다.

이미지 다시 보기

라이트 필드는 공간적, 각도적 정보를 제공하기 때문에 이미지 후처리에 의해 노출 후 초점 평면의 위치를 변경할 수 있는데, 이를 리커싱(refocusing)이라고 부르기도 한다. 리커싱의 주체는 일체형 변환을 통해 라이트 필드에서 기존의 2-D 사진을 얻는 것이다. 변환은 광원을 입력으로 삼고 결정된 평면에 초점을 맞춘 사진을 생성한다.

Assume we use $L_{F}(s,t,u,v)$ to represent a 4-D light field that records light rays traveling from position $(u,v)$ on the first plane to position $(s,t)$ on the second plane, where $F$ is the distance between two 비행기들 $\alpha F$ $\alpha F$ $\alpha F$ 깊이의 2-D 사진은 다음과 같은 적분 변환에서 얻을 수 있다 $\alpha F$ .^[2]

${\mathcal {P}}_{\alpha }\left[L_{F}\right](s,t)={1 \over \alpha ^{2}F^{2}}\iint L_{F}(u(1-1/\alpha )+s/\alpha ,v(1-1/\alpha )+t/\alpha ,u,v)~dudv$ ,

또는 더 간결하게,

${\displaystyle {\mathcal {P}}_{\alpha }\left[L_{F}\right]({\boldsymbol {s}})={\frac {1}{\alpha ^{2}F^{2}}}\int L_{F}\left({\boldsymbol {u}}\left(1-{\frac {1}{\alpha }}\right)+{\frac {\boldsymbol {s}}{\alpha }},{\boldsymb$ $ol{u}\오른쪽)d{\\symbol{u$

where ${\boldsymbol {s}}=(s,t)$ , ${\boldsymbol {u}}=(u,v)$ , and ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ is often referred to as Photography operator.

In practice, this formula cannot be directly used because a plenoptic camera usually captures discrete samples of the lightfield $L_{F}(s,t,u,v)$ , and hence resampling (or interpolation) is needed to compute ${\displaystyle L_{F}\left({\bold$ $기호 {u}\{\frac{1}{\alpha }}\오른쪽)+{\frac {\boldsymbol{s}{\alpha$ }}}{\ $boldsymbol {u$ 또 다른 문제는 높은 계산 복잡성이다. $N\times N\times N\times N$ $N\times N\times N\times N$ $N\times N\times N\times N$ $N\times N$ $N\times N\times N\times N$ $N\times N\times N\times N$ × N $N\times N\times N\times N$ $N\times N\times N\times N$ {\ $displaystyle N}$ $2-D$ 사진을 계산하려면 N × N × N ${\displaystyle N\times$ N} 4-D $N\times N\times N\times N$ 광원 필드에서 수식의 $O(N^{4})$ 는 $O(N^{4})$ O ( $O(N^{4})$ 4 $O(N^{4})$ ) {\ $displaystystyle$ O( $N^{4$ }})이다 $O(N^{4})$ ^[2]

푸리에 슬라이스 사진

계산의 복잡성을 줄이는 한 가지 방법은 푸리에 슬라이스 정리 개념을 채택하는 것이다.^[2] 사진 연산자 ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ [ ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ ${\$ 은(는) 투영에 따른 전단(shear)으로 볼 수 있으며 ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ , 결과는 광장의 4-D 푸리에 변환의 확장된 2-D 슬라이스에 비례해야 한다. 보다 정확히 말하면, 2-D 슬라이스를 추출하고 역 2-D 변환을 적용하고 스케일링을 적용하여 조명 영역의 4-D 푸리에 스펙트럼에서 다시 집중된 영상을 생성할 수 있다. 알고리즘의 점증상 복잡도는 $O(N^{2}\operatorname {log} N)$ $O(N^{2}\operatorname {log} N)$ $O(N^{2}\operatorname {log} N)$ $O(N^{2}\operatorname {log} N)$ $O(N^{2}\operatorname {log} N)$ ) $O(N^{2}\operatorname {log}N)$ 이다 $O(N^{2}\operatorname {log} N)$ 자세한 내용은 Fourier Slice Photographic을 참조하십시오.

이산 초점 스택 변환

2-D 사진을 효율적으로 계산하는 또 다른 방법은 이산 초점 스택 변환(DFST)을 채택하는 것이다.^[3] 더 정확히 말하면, DFST는 리포커스된 2-D 사진 모음, 즉 이른바 포커스 스택을 생성하도록 설계되었다. 이 방법은 FrFT(Fast fractal fourier transform)에 의해 구현될 수 있다.

The discrete photography operator ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ is defined as follows for a lightfield $L_{F}({\boldsymbol {s}},{\boldsymbol {u}})$ sampled in a 4-D grid ${\disp$ $laystyle {\boldsymbol {s}}=\Delta s{\tilde {\boldsymbol {s}}},{\tilde {\boldsymbol {s}}}=-{\boldsymbol {n}}_{\boldsymbol {s}},...,{\boldsymbol {n}}_{\boldsymbol {s}}}$ , ${\displaystyle {\boldsymbol {u}}=\Delta u{\tilde {\boldsymbol {u}}},{\tilde {\boldsymbol {u}}}=-{\boldsymbol$ ${n}_{\symbol{u}},...,$ {\ $symbol{n}_{\symbol{u}}}$ :

${\mathcal {P}}_{q}[L]({\boldsymbol {s}})=\sum _{{\tilde {\boldsymbol {u}}}=-{\boldsymbol {n}}_{\boldsymbol {u}}}^{{\boldsymbol {n}}_{\boldsymbol {u}}}L({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})\델타 {\boldsymbol {u},\quad \델타 {\boldsymbol {u}}=\Delta u\Delta v,\q=\left(1-{\frac {1}{\alpha }}\오른쪽)}$

$({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})$ $({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})$ + $({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})$ , $({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})$ ) ${\displaystyle({\boldsymbol {u}q+{\boldsymbol {s},{\boldsymbol {u})$ 은 대개 4-D 그리드에 있지 않기 $({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})$ 때문에 DFST는 비그리드 값을 계산하기 위해 삼각 보간법을 채택한다.

전체 알고리즘은 다음 6단계로 구성된다.

Sample the light field $L_{F}({\boldsymbol {s}},{\boldsymbol {u}})$ with the sampling period $\Delta s$ and $\Delta u$ and get the discretized light field $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ .
0을 포함한 $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ 패딩 $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ , $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ ) ${\displaystyle L_{F}^{d}({\boldsymbol{s},{\boldsymbol{u})$ 는 앨리어싱 없이 FrFT에 충분한 신호 길이입니다.
모든 ${\boldsymbol {u}}$ {\ $displaystyle$ {\ $boldsymbol$ { $u}}$ 에 대해 ${\boldsymbol {u}}$ $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ ) ${\displaystyle L_{F}^{d}({\boldsymbol {s},{\boldsymbol$ 의 이산 푸리에 변환을 계산하고 $R1$ $R1{\\daystymb$
모든 초점 길이 $\alpha F$ $\alpha F$ $\alpha F$ 에 대해 $R1$ $R1$ ${\displaystyle R1$ }의 $R1$ 분수 푸리에 변환을 계산하십시오 $R1$ 여기서 변환 순서는 $\alpha$ ${\displaystyle \alpha$ $\alpha$ 에 따라 달라지고 결과 $R2$ 2 ${\displaystystyle R2}$ 을 얻으십시오 $R2$
$R2$ $R2$ $R2$ 의 역 이산 푸리에 변환을 계산하십시오 $R2$
$R2$ 2 $R2$ 의 주변 픽셀을 제거하여 $R2$ 각 2-D 사진의 크기 $(2{n}_{\boldsymbol {s}}+1)\times (2{n}_{\boldsymbol {s}}+1)$ $(2{n}_{\boldsymbol {s}}+1)\times (2{n}_{\boldsymbol {s}}+1)$ + $(2{n}_{\boldsymbol {s}}+1)\times (2{n}_{\boldsymbol {s}}+1)$ ) $(2{n}_{\boldsymbol {s}}+1)\times (2{n}_{\boldsymbol {s}}+1)$ + $(2{n}_{\boldsymbol {s}}+1)\times (2{n}_{\boldsymbol {s}}+1)$ ) ${\displaystyle(2{n}_{\boldsymbol{s}+1)\time(2{n}_{\boldsymboldmbol{s}}}}}}:{$ s}+1)을 갖도록 하십시오 $.$

라이트 필드 작성 방법

광장은 빛의 근본적 표현이다. 이와 같이, 광장을 만들 수 있는 방법에는 이미지나 그것을 캡처할 수 있는 기구를 만들 수 있는 컴퓨터 프로그램이 있는 만큼 여러 가지가 있다.

컴퓨터 그래픽에서 라이트 필드는 일반적으로 3D 모델을 렌더링하거나 실제 장면을 촬영하여 생산된다. 어느 경우든 광원 뷰를 생성하려면 많은 관점을 수집해야 한다. 채택된 매개변수화에 따라, 구조화되지 않은 관점 수집도 가능하지만, 이 수집은 일반적으로 선, 원, 평면, 구체 또는 다른 형태의 일부에 걸쳐진다(Builer 2001).

광장을 사진 촬영하기 위한 장치에는 움직이는 휴대용 카메라 또는 로봇으로 제어되는 카메라(Levoy 2002), 카메라 호(매트릭스에서 사용되는 총알 시간 효과), 카메라의 밀집 배열(Kanade 1998; Yang 2002; Wilburn 2005), 휴대용 카메라(ng 2005; Georgieve 2006; Marwah 2013), 현미경(Levoy 200)이 포함될 수 있다.6) 또는 기타 광학 시스템(볼링 1987).

조명 영역에 몇 개의 이미지가 있어야 하는가? (미켈란젤로의 밤 조각상 중) 가장 큰 것으로 알려진 광원에는 2만 4천 개의 1.3 메가픽셀 이미지가 포함되어 있다. 더 깊은 수준에서 답은 응용 프로그램에 따라 달라진다. 광원 렌더링의 경우(아래 애플리케이션 섹션 참조) 불투명 물체를 완전히 둘러보려면 물론 뒷면을 촬영해야 한다. 덜 분명한 것은, 물체 가까이 걸어가고자 할 때 물체가 st 평면에 가로놓여 있다면, 당신은 지금 당신 뒤에 있는 Uv 평면의 미세한 간격의 위치(위의 2-평면 매개변수화에서)가 필요하고, 이 이미지들은 높은 공간 해상도를 가져야 한다는 것이다.

라이트 필드에서 영상의 수와 배열, 각 영상의 해상도를 함께 4D 라이트 필드의 "샘플링"이라고 한다. 광장 샘플링에 대한 분석은 많은 연구자들에 의해 수행되었다. 좋은 출발점은 차이(2000)이다. 폐색 효과로는 두란드(2005)가, 조명 효과와 반사 효과로는 라마모르티(2006)가, 플롭틱 카메라와 3D 디스플레이 애플리케이션으로는 Ng(2005)와 Zwicker(2006)가 각각 관심사다.

적용들

컴퓨터 이미징(computering imaging)은 디지털 컴퓨터와 관련된 모든 이미지 형성 방법을 말한다. 이러한 방법들 중 많은 것들이 가시적인 파장에서 작동하며, 그러한 방법들 중 많은 것들이 광장을 생성한다. 결과적으로, 광장의 모든 응용 프로그램을 나열하려면 미술, 과학, 공학 및 의학에서 컴퓨터 이미징의 모든 사용을 조사해야 할 것이다. 컴퓨터 그래픽에서 일부 선택된 애플리케이션은 다음과 같다.

아래쪽을 향한 광원(F-F')은 일조 강도 벡터가 바깥쪽으로 구부러지는 광장을 유도한다. 게르순은 미적분을 이용하여 표면의 점(P₁₂, P)에 떨어지는 일조 강도를 계산할 수 있었다. (게르순, 그림 24)

조명 엔지니어링: 거쉰이 광장을 연구한 이유는 이러한 표면 위에 위치한 다양한 모양의 광원으로 인해 표면에서 관찰되는 조명 패턴을 도출(가능한 경우 닫힌 형태로)하기 위해서였다. 오른쪽에는 예가 나와 있다. 좀 더 현대적인 연구는 (Ashdown 1993)이다.

조명 공학에 전념하는 광학 분야는 비이미징 광학이다(Chave 2015; Winston 2005). 플로우 라인(게르순의 플럭스 라인)과 벡터 플럭스(게르순의 라이트 벡터)의 개념을 광범위하게 사용한다. 그러나 광장(이 경우 광선을 정의하는 위치와 방향)은 위상 공간과 해밀턴 광학 측면에서 일반적으로 설명된다.

라이트 필드 렌더링: 장면의 4D 라이트 필드에서 적절한 2D 슬라이스를 추출하면 장면의 참신한 뷰를 연출할 수 있다(Levoy 1996; Gortler 1996). 광장과 슬라이스의 매개변수화에 따라 이러한 보기는 원근법, 맞춤법, 교차 슬롯(Zomet 2003), 일반 선형 카메라(Yu 및 McMillan 2004), 다중 내성(Rademacher 1998) 또는 다른 유형의 투영일 수 있다. 라이트 필드 렌더링은 이미지 기반 렌더링의 한 형태다.
합성 조리개 사진: 검체의 적절한 4D 부분집합을 광장에 통합함으로써, 유한한 (즉, 핀홀이 아닌) 조리개를 가진 카메라가 포착할 수 있는 뷰를 대략적으로 추정할 수 있다. 그러한 견해는 한정된 영역의 깊이를 가지고 있다. 이 통합을 수행하기 전에 광장을 깎거나 뒤틀면 장면에서 서로 다른 전면 평행(Isaksen 2000) 또는 사선(Vaish 2005) 평면에 집중할 수 있다. 만약 디지털 카메라가 광원을 포착할 수 있다면(2005년 ng) 그 사진들은 촬영된 후에 다시 초점이 맞춰질 수 있을 것이다.
3D 디스플레이: 물리적 공간에서 각 시료를 적절한 광선에 매핑하는 기술을 이용해 광장을 제시함으로써 원 장면을 보는 것과 유사한 자동보경 시각효과를 얻는다. 이를 위한 비디지털 기술로는 일체형 사진, 시차 파노라마그램, 홀로그래피 등이 있다. 디지털 기술로는 고해상도 디스플레이 화면 위에 렌즈 배열을 배치하거나 비디오 프로젝터를 사용하여 이미지를 렌즈 배열에 투사하는 것을 포함한다. 후자를 비디오 카메라의 배열과 결합하면 시간이 걸리는 광원을 캡처해 표시할 수 있다. 이것은 본질적으로 3D 텔레비전 시스템을 구성한다(Javidi 2002; Matusik 2004).
뇌 영상촬영: 신경활동은 실시간 칼슘 이온의 존재를 나타내는 GCaMP와 같이 가역형 형광 마커로 뉴런을 유전적으로 부호화하여 광학적으로 기록할 수 있다. 경장 현미경 검사에서는 전량 정보를 하나의 프레임에 담아내기 때문에 비디오 프레임에서 대량으로 랜덤하게 분포된 많은 개별 뉴런의 신경 활동을 감시할 수 있다(그로세닉, 2009, 2017; 페레스, 2015). 신경 활동에 대한 정량적 측정은 뇌 조직에서 광학적 이상에도 불구하고 볼륨 이미지를 재구성하지 않고도 수행할 수 있으며(Pegard, 2016), 동작하는 포유류에서 수천 개의 뉴런의 활동을 모니터링하는 데 사용된다(Grosenick, 2017).
일반화된 장면 재구성: GSR(Generalized Scene Reconstruction, GSR)은 일반화된 조명 영역과 조명 가능한 물질 영역을 나타내는 장면 모델이 생성되는 다중 영상에서 3D 재구성 방법이다(Leffingwell, 2018). 광장은 장면의 모든 지점을 통해 사방으로 흐르는 빛을 나타낸다. 물질 분야는 현장의 모든 지점을 점유하는 물질의 빛 상호작용 특성을 나타낸다. GSR은 Neural Radiance Fields(NeRFs) (Mildenhall, 2020), Plenoxels (Yu & Fridovich-Keil, 2021), Inverse Light Transport (Leffingwell, 2018) 등의 접근법을 사용하여 수행할 수 있다.

홀로그램용 합성 이미지의 영상 생성과 선구성은 컴퓨터 광장의 가장 초기 사례 중 하나로, 레보이와 한라한의 작품에 사용된 기하학을 예측하고 나중에 동기를 부여한다(Halle 1991, 1994).

광전광 디스플레이에 대한 현대적 접근방식은 고해상도, 증가된 대비, 넓은 시야 및 기타 편익을 달성하기 위한 광학 요소와 압축 연산의 공동 설계를 탐구한다(Wetzstein 2012, 2011; Lanman 2011, 2010).

눈부심 감소: 눈부심은 카메라의 몸체와 렌즈 광학 내부에 빛이 여러 번 산란되어 발생하며 영상 대비를 감소시킨다. 섬광은 2D 영상 공간(Talvala 2007)에서 분석했지만, 4D 광 공간 현상(Raskar 2008)으로 식별하는 것이 유용하다. 카메라 내부의 광선 공간을 통계적으로 분석해 눈부심 유물을 분류해 제거할 수 있다. 광 공간에서 섬광은 고주파 노이즈로 작용하며 특이치 제거로 감소할 수 있다. 이런 분석은 카메라 내부의 광장을 포착해 수행할 수 있지만 공간 분해능이 상실되는 결과를 초래한다. 균일하고 균일하지 않은 광선 샘플링을 사용하여 영상 해상도를 크게 저하시키지 않고 섬광을 줄일 수 있다(Raskar 2008).

참고 항목

메모들

^ Faraday, Michael (30 April 2009). "LIV. Thoughts on ray-vibrations". Philosophical Magazine. Series 3. 28 (188): 345–350. doi:10.1080/14786444608645431. Archived from the original on 2013-02-18.
^ ^a ^b ^c Ng, R. (2005) 푸리에 슬라이스 사진. ACM SIGRAPH 2005 논문 (pp. 735-7444)에서.
^ Nava, F. Pérez; Marichal-Hernández, J.G.; Rodríguez-Ramos, J.M. (August 2008). "The Discrete Focal Stack Transform". 2008 16th European Signal Processing Conference: 1–5.

참조

이론

아델슨, E.H., 버겐, J.R. (1991) "플레놉틱 기능과 초기 시력의 요소" 시각 처리, M. 랜디 및 J.A.의 계산 모델에서. Movshon, Eds, MIT Press, 1991년 캠브리지, 페이지 3-20.
아르보, J. (1994년). "부분적으로 가려진 다면원을 위한 방사조도 자코비안", Proc. ACM SIGRAPH, ACM Press, 페이지 335–342.
볼레스, R.C., 베이커, H. H., 마리몬트, D.H. (1987년) "극상 평면 영상 분석: "운동을 통한 구조 결정에 대한 접근" 컴퓨터 비전 국제 저널 제1권 1987호 클루워 학술 출판사 페이지 7~55.
패러데이, M, "레이 진동에 대한 생각" 철학적 잡지, S.3, Vol XXVIII, N188, 5월 1846년 5월.
거순, A. (1936년) 1936년 모스크바의 "빛의 들판" P에 의해 번역되었다. 문과 G. Timoshenko, Journal of Math and Physics, Vol. 16세, MIT, 1939, 페이지 51–151.
Gortler, S.J., Greszczuk, R., Szeliski, R., Cohen, M. (1996년) "The Lumigraph", Proc. ACM SIGRAPH, ACM Press, 페이지 43–54.
레보이, M, 한라한, P. (1996년) "Light Field Rendering", Proc. ACM SIGRAPH, ACM Press, 페이지 31-42.
문, P, 스펜서, D.E.(1981) 포토 필드, MIT 프레스.
Wong, T.T., Fu, C.W., Hung, P.A., Leung C.S. (2002) "플레놉틱-조명 기능", IEEE 트랜스. 멀티미디어, 제4권, 제3권, 페이지 361-371.

분석

G. Wetzstein, I. Ihrke, W. Heidrich(2013) "플레놉틱 멀티플렉싱 및 재구성", 국제 컴퓨터 비전 저널(IJCV), 제101권, 제2, 페이지 384–400.
라마모오르티, R, 마하얀, D, 벨후메우르, P. (2006) "조명, 음영 및 그림자의 첫 번째 순서 분석", ACM TOG.
Zwicker, M, Matusik, W, Durand, F, Pfister, H. (2006년) 2006년 렌더링에 관한 유로그래픽스 심포지엄 "Antialiasing for automultiscopic 3D Displays".
Ng, R. (2005) "Fourier Slice Photography", Proc. ACM SIGRAPH, ACM Press, 페이지 735-744.
듀랜드, F, 홀츠추치, N, 솔러, C, 찬, E, 릴리온, F. X. (2005) "광수송의 주파수 분석", Proc. ACM SIGRAPH, ACM Press, 페이지 1115–1126.
차이, J-X, 통, X, 찬, S.C, Shum, H. (2000) "플레놉틱 샘플링", Proc. ACM SIGRAPH, ACM Press, 페이지 307–318.
할레, M. (1994) SPIE Proc에서 "Hologram as Islated Imaging Systems".^{[permanent dead link]} 제2176권: 실용 홀로그래피 8호, S.A. 벤튼, 에드, 페이지 73–84.
유, J, 맥밀런, L. (2004) "일반 선형 카메라", Proc. ECCV 2004, 컴퓨터 과학 강의 노트, 페이지 14–27.

라이트 필드 카메라

마르와, K, 웨츠슈타인, G, 반도, Y, 라스카르, R. (2013) "과다완성 사전과 최적화된 투영을 이용한 압축 광원 촬영", ACM Transactions on Graphics(SIGGRAPH)이다.
량, C.K., 린, T.H., 웡, B.Y., 류, C. 첸, H. H. (2008) "프로그래밍 가능한 애퍼처 사진:멀티플렉스 광장 획득", Proc. ACM SIGRAPH.
비하라가반, A, Raskar, R, Agrawal, A, Mohan, A, Tumblin, J. (2007) "Dappled Photography: Mask Enhanced Cameras for Herethoded Light Fields and Coded Apropure Refocusing", Proc. ACM SIGRAPH.
조지예프, T, 정, C, 나야르, S, 커리스, B, 세일린, D, 인트왈라, C. (2006) Proc, "Integramme Photography에서 Spatio-angular Resolution-offs". EGSR 2006.
카나데, T, 사이토, H, 베둘라, S. (1998년) "3D 룸: 다중 비디오 스트림을 동기화하여 시간 분산 3D 이벤트 디지털화"라고 기술 보고서 CMU-RI-TR-98-34, 1998년 12월.
레보이, M. (2002) 스탠포드 구면 갠트리
Levoy, M, Ng, R, Adams, A, Footer, M, Horowitz, M. (2006) "라이트 필드 현미경", ACM Transactions on Graphics(Proc) SIGGRAPH), 제25권, 제3권.
응, R, 레보이, M, 브레디프, M, 듀발, G, 호로위츠, M, 한라한, P. (2005) 2005년 4월, Stanford Tech Report CTSR 2005-02, "Hand-Hold Plenoptic Camera를 사용한 라이트 필드 사진기".
윌번, B, Joshi, N, V, Talvala, E, Antunez, E, Barth, A, Adams, A, Levoy, M, Horowitz, M. (2005) "대형 카메라 어레이를 사용한 고성능 이미지", ACM Transactions on Graphics(Proc) SIGGRAPH), 제24권, 제3권, 페이지 765–776.
양, J, C, 에버렛, M, 뷸러, C, 맥밀런, L. (2002) "A Real-Time Distributed Light Field Camera", Proc. 유로그래픽 렌더링 워크샵 2002.
"CAFADIS 카메라"

라이트 필드 표시

Wetzstein, G, Lanman, D, Hirsch, M, Raskar, R. (2012) "텐서 디스플레이: 멀티레이어 디스플레이와 방향 백라이닝을 이용한 압축 광장 디스플레이", 그래픽상의 ACM 트랜잭션(SIGGRAPH)
Wetzstein, G, Lanman, D, Heidrich, W, Raskar, R.(2011년). ACM Transactions on Graphics(SIGGRAPH) "레이어드 3D: 감쇠 기반 광장 및 고동적 범위 디스플레이용 단층 영상 합성"
Lanman, D, Wetzstein, G, Hirsch, M, Heidrich, W, Raskar, R.(2011년). "극화 필드: 다층 LCD를 이용한 동적 광원 디스플레이," 그래픽상의 ACM 트랜잭션 (SIGGRAPH Asia)
란만, D, 허쉬, M. Kim, Y, Raskar, R. (2010) "HR3D: 콘텐츠-어댑티브 시알락스 장벽을 이용한 이중 적층 LCD 하이랭크 3D 디스플레이를 이용한 유리 없는 3D 디스플레이", ACM on Graphics(SIGRAPH Asia)
마투식, W, 피스터, H. (2004) "3D TV: 동적 장면의 실시간 획득, 전송 및 자동 역학 디스플레이를 위한 확장 가능한 시스템", Proc. ACM SIGRAPH, ACM Press.
자비디, B, 오카노, F, 에드. (2002) 3차원 텔레비전, 비디오 및 디스플레이 기술, 스프링거-버래그.
클룩, M, 버넷, T, 판셀로, A, 히스, A, 가드너, K, 오코넬, S, 뉴스왕거, C. (2013년) SID 심포지엄 기술논문 요약본 "확장성, 협업성, 대화형 광장 디스플레이 시스템"
Fattal, D, Peng, Z, Tran, T, Vo, S, Fiorentino, M, Brug, J, Beausoleil, R. (2013) "광각 안경 없는 3차원 디스플레이를 위한 다방향 백라이트", Nature 495, 348–351

라이트 필드 아카이브

적용들

그로세닉, L, 앤더슨, T, Smith S. J.(2009) "뉴런 앙상블의 생체내 영상 촬영을 위한 탄성 소스 선택" 나노에서 매크로로, 제6회 IEEE 국제 바이오메디컬 영상 심포지엄. (2009) 1263–1266.
Grosenick, L., Broxton, M., Kim, C. K., Liston, C., Poole, B., Yang, S., Andalman, A., Scharff, E., Cohen, N., Yizhar, O., Ramakrishnan, C., Ganguli, S., Suppes, P., Levoy, M., Deisseroth, K. (2017) "Identification of cellular-activity dynamics across large tissue volumes in the mammalian brain" bioRxiv 132688; doi: https://doi.org/10.1101/132688.
Heide, F, Wetzstein, G, Raskar, R., Heidrich, W.(2013) "압축형 디스플레이를 위한 적응형 이미지 합성", ACM Transactions on Graphics(SIGGRAPH)
W. (2011), Wetzstein, G, Raskar, R, Heidrich, W. (2011) "Light Field Probe를 이용한 핸드헬드 Schlieren Photography", IEEEE International Conference on Computing Photography(ICP)
페레스, F, 마리찰, J.G, 로드리게스, J.M. (2008) 이산 초점 스택 변환, Proc. EUSIPCO
Raskar, R, Agrawal, A, Wilson, C, Veerarahagavan, A. (2008). "Glare Awareness Photography: 카메라 렌즈의 눈부심 효과 저감을 위한 4D Ray 샘플링", Proc. ACM SIGRAPH.
탈발라, E-V, 아담스, A, 호로위츠, M, 레보이, M. (2007) "하이 다이내믹 레인지 이미징의 눈부심", Proc. ACM SIGRAPH.
할리, M, 벤튼, S, 클럭, M, 언더코플러, J. (1991년) "울트라그램: 일반화된 홀로그래피 스테레오그램", SPIE 1461, 실용 홀로그래피 V, S.A. 벤튼, 에드. 페이지 142–155.^{[permanent dead link]}
조메트, A, 펠드만, D, 펠레그, S, 와인샬, D. (2003) "모자이싱 새로운 관점: 교차-슬릿 투영", IEEE 패턴 분석 및 기계 인텔리전스에 관한 IEEE 거래 (Patternal Analysis and Machine Intelligence, PAMI), 2003년 6월, 페이지 741–754.
바이쉬, 브이, 가르그, G, 탈발라, E, 안투네즈, E, 윌번, B, 호로위츠, M, 레보이, M. (2005) "보기 변환의 전단-워프 인자화를 이용한 합성 개구부", Proc. CVPR 2005와 함께 안전 및 보안을 위한 Advanced 3D Imaging에 대한 워크샵.
베다드, N, 쇼프, T, 호베르만, A, 하랄람, M, 샤이크, N, 코바체비치, J, 발람, N, 토시치, I. (2016) "중이의 3D 생체내 영상촬영을 위한 광장오시스코프 설계" 생물 의학 광학 익스프레스, 8(1) 페이지 260–272.
카리지아니, S, 마르티넬로, M, 스피놀라스, L, Frossard, P, Tosic, I. (2018) "광장 데이터에서 자동 고막 등록" IEEE 이미지 처리 국제 회의(ICIP)
Rademacher, P, Bishop, G. (1998년) "Multiple-Center-of-Projection Images", Proc. ACM SIGRAPH, ACM Press.
이삭센, A, 맥밀런, L, 고틀러, S.J. (2000) "동역학적으로 재결정된 광원", Proc. ACM SIGRAPH, ACM Press, 페이지 297–306.
뷸러, C, Bosse, M, McMillan, L, Gortler, S, Cohen, M. (2001) "구조되지 않은 루미그래프 렌더링", Proc. ACM SIGRAPH, ACM Press.
애쉬다운, I.(1993) "Near-Field Photometry: A New approach", Lighting Engineering Society, Vol. 22, No. 1, Winter, 1993, 페이지 163–180.
채브스, J. (2015) "비이미징 광학 소개, 제2판", CRC 프레스
윈스턴, R, 미냐노, J.C., 베니테즈, P.G., 샤츠, N., 보르츠, J.C. (2005) "비이미징 광학", 학술 출판사
Pégard, N. C., 류H.Y., Antiata, N., Gerlock M., Adesnik, H., Waller, L. 3D 신경 활동 기록을 위한 압축 광장 현미경. Optica 3, 5번 페이지 517–524 (2016).
레핑웰, J, 메거, D, 마흐무드, K, 애커슨, S. (2018) "일반화된 장면 재구성." arXiv:1803.08496v3 [cs.CV, 페이지 1-13.
밀덴홀, B, 스리니바산, P. P., 탄식, M, 바론, J. T. 라마모시, R., & Ng, R. (2020) "NeRF : 시야 합성을 위한 신경 방사장으로 장면을 표현한다." Computer Vision – ECCV 2020, 405–421.
유, A, 프리도비치-킬, S, 탄식, M, 첸, Q, 레흐트, B, 가나자와, A.(2021년) "플레녹셀: 신경망이 없는 광도장." ArXiv:211.11215, 페이지 1-25
Perez, CC; Lauri, A; et al. (September 2015). "Calcium neuroimaging in behaving zebrafish larvae using a turn-key light field camera". Journal of Biomedical Optics. 20 (9): 096009. Bibcode:2015JBO....20i6009C. doi:10.1117/1.JBO.20.9.096009. PMID 26358822.
페레즈, C. C., 로리, A., Symvoulidis, P, Capetta, M., Erdmann, A., & Westmeyer, G. G. G. (2015) 턴키 라이트 필드 카메라를 사용하여 제브라피쉬 유충을 동작시키는 칼슘 신경영상. 생물 의학 광학 저널, 20(9), 096009-096009.

레온, K, 갈비스, L, 아겔로, H. (2016) "2D 투영에서 색상으로 코딩된 개구부를 사용한 압축 감지를 기반으로 한 다중 스펙트럼 광장의 재구성(5d 플레놉틱 기능)" Revista Compad de Inseniieriaa Universidad de Antioquia 80, 페이지 131.

[1] Faraday, Michael (30 April 2009). "LIV. Thoughts on ray-vibrations". Philosophical Magazine. Series 3. 28 (188): 345–350. doi:10.1080/14786444608645431. Archived from the original on 2013-02-18.

[renng-2] Ng, R. (2005) 푸리에 슬라이스 사진. ACM SIGRAPH 2005 논문 (pp. 735-7444)에서.

[3] Nava, F. Pérez; Marichal-Hernández, J.G.; Rodríguez-Ramos, J.M. (August 2008). "The Discrete Focal Stack Transform". 2008 16th European Signal Processing Conference: 1–5.

[1]

[2]

[3]

Search