여러 영상에서 3D 재구성

마두로담 미니어처 파크가 Fantasitron 포토 부스에서 촬영한 2D 사진으로부터 석고 베이스의 프린팅을 사용해 Shapeways가 제작한 1:20 스케일의 3D 셀카.

마두로담 Fantasitron 3D 포토부스에서 촬영한 2D 사진으로 3D 모델을 생성

단일 또는 다중 뷰 깊이 지도 또는 실루엣에서 3D 모양 생성 및 재구성

여러 영상에서 3D 재구성은 영상 세트에서 3차원 모델을 만드는 것입니다.3D 장면에서 2D 영상을 얻는 역공정입니다.

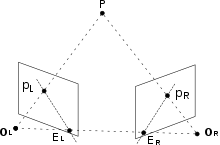
이미지의 본질은 3D 장면에서 2D 평면으로 투영하는 것이며, 이 과정에서 깊이가 손실됩니다.특정 영상 지점에 해당하는 3D 지점은 시선 위에 있도록 제한됩니다.단일 이미지로는 이 선의 어떤 점이 이미지 포인트에 해당하는지 판단할 수 없습니다.두 개의 영상을 사용할 수 있는 경우 3D 지점의 위치를 두 개의 투영 광선의 교차점으로 찾을 수 있습니다.이 과정을 삼각 측량이라고 합니다.이 프로세스의 핵심은 대응하는 포인트 세트가 어떤 구조를 포함해야 하며 이 구조가 카메라의 포즈 및 보정과 관련이 있다는 정보를 전달하는 여러 뷰 간의 관계입니다.

최근 수십 년 동안 컴퓨터 그래픽, 가상 현실 및 통신을 위한 3D 컨텐츠에 대한 중요한 수요가 있어 요구 사항에 대한 강조의 변화가 촉발되었습니다.3D 모델 구축을 위한 많은 기존 시스템은 특수 하드웨어(예: 스테레오 리그)를 중심으로 구축되어 있어 새로운 애플리케이션의 요구사항을 충족할 수 없는 고비용이 발생합니다.이 간격은 디지털 이미징 설비(카메라 등)의 사용을 촉진합니다.초기 방법은 토마시와 ^[2]카나데에 의해 제안되었다.그들은 영상 시퀀스에서 3D를 추출하기 위해 아핀 인수분해 방식을 사용했다.그러나 맞춤법 투영의 가정은 이 시스템의 중요한 제한 사항입니다.

처리.

시각 선체는 객체의 ^[3]여러 실루엣에서 재구성할 수 있습니다.

여러 2D 영상을 3D 모델로 변환하는 작업은 일련의 처리 단계로 구성됩니다.

카메라 보정은 내적 파라미터와 외적 파라미터로 구성되며, 이 파라미터가 없으면 어떤 알고리즘 배열도 동작하지 않습니다.Calibration(보정)과 Depth(깊이) 결정 사이의 점선은 일반적으로 깊이 결정에 카메라 보정이 필요하다는 것을 나타냅니다.

깊이 측정은 전체 공정에서 가장 어려운 부분으로, 주어진 이미지(깊이)에서 누락된 3D 구성요소를 계산하기 때문입니다.일치된 요소의 위치를 3D 공간에서 삼각 측량할 수 있도록 두 이미지 간의 일치 항목을 찾는 대응 문제가 여기서 중요한 문제입니다.

여러 개의 깊이 맵이 있으면 깊이 계산 및 카메라 밖으로 투영하여 최종 메쉬를 작성하기 위해 이들을 조합해야 합니다.카메라 보정은 깊이 지도에 의해 생성된 많은 메쉬를 조합하여 더 큰 메쉬를 개발할 수 있는 위치를 식별하기 위해 사용되며, 관찰을 위해 두 개 이상의 뷰를 제공합니다.

재료 도포 단계에는 최종 목표가 될 수 있는 완전한 3D 메쉬가 있지만, 일반적으로 원본 사진의 색상을 메쉬에 적용하고자 합니다.여기에는 이미지를 메쉬에 랜덤하게 투영하는 것부터 초해상도 텍스처를 조합하는 방법, 마지막으로 스펙큘러 특성이나 확산 특성 등의 재료별로 메쉬를 분할하는 방법 등이 있습니다.

재건에 대한 수학적 설명

행렬 $\{P^{i}\}_{i=1\ldots N}$ { $\{P^{i}\}_{i=1\ldots N}$ $\{P^{i}\}_{i=1\ldots N}$ $\{P^{i}\}_{i=1\ldots N}$ $\{P^{i}\}_{i=1\ldots N}$ … $\{P^{i}\}_{i=1\ldots N}$ {\ $displaystyle \{P^{i}\}_{i=1\ldots$ N $\{P^{i}\}_{i=1\ldots N}$ 을(를) 가진 N카메라에 의해 3D 점 그룹이 주어진 $m_{j}^{i}\simeq P^{i}w_{j}$ , $m_{j}^{i}\simeq P^{i}w_{j}$ {\ $displaystyle m_{j}^{i}\displayq P^{w}_{j}$ _{j}}_{j}}}}_ $m_{j}^{i}\simeq P^{i}w_{j}$ { $m_{j}^{i}\simeq P^{i}w_{j}$ }}개의 동일 좌표계를 $m_{j}^{i}\simeq P^{i}w_{j}$ 한다. ${\displaystyle$ i $^{th}}$ 카메라 $i^{th}$ .재구성 문제는 픽셀 좌표 그룹 { $\{m_{j}^{i}\}$ ji $\{m_{j}^{i}\}$ { $displaystyle$ \{ $m_{j}^{i$ 에 $\{w_{j}\}$ 따라 다음과 같이 변경할 수 있습니다. 카메라 $\{P^{i}\}$ $\{P^{i}\}$ $}$ { $displaystyle$ \{ $P^{i}\}}$ 및 $\{P^{i}\}$ 씬 $\{w_{j}\}$ 구조 { $\{w_{j}\}$ { $displaystyle \w_{j}}}$ {displaystyle \}

m_{j}^{i}\simeq P^{i}w_{j}

m_{j}^{i}\simeq P^{i}w_{j}

i

m_{j}^{i}\simeq P^{i}w_{j}

m_{j}^{i}\simeq P^{i}w_{j}

m_{j}^{i}\simeq P^{i}w_{j}

j {

display

style

m_{j}^{i}\simeq

P

^{i}w_{j}}

(1)

일반적으로 더 이상의 제한 없이 투영적인 ^[4]^[5]재건을 획득합니다. $\{P^{i}\}$ $\{P^{i}\}$ $}$ { $displaystyle$ \ { $P^$ { $i$ } $\{w_{j}\}$ 및 $\{P^{i}\}$ { w $\{w_{j}\}$ $}$ { $display$ style \ { w $_$ { $j$ }}이 $\{w_{j}\}$ $\{P^{i}T\}$ 가) (1)을 만족하는 경우 { $\{P^{i}T\}$ T $}$ { $displaystyle$ \ { $P^$ { $i$ }T $\}$ 및 $\{P^{i}T\}$ $\{T^{-1}w_{j}\}$ { $\{T^{-1}w_{j}\}$ - $\{T^{-1}w_{j}\}$ $\{T^{-1}w_{j}\}$ $\{T^{-1}w_{j}\}$ $}$ ({ $displaystyle$ \ { T^ { - 1 $\{T^{-1}w_{j}\}$ } $\{T^{-1}w_{j}\}$ w _ { j $}$ \ } )는 $\{T^{{-1}}w_{j}\}$ 임의의 4 × 4 비칭 행렬 T에서 (1)을 만족합니다.

투영 재구성은 사전 정보 없이 점의 대응만으로 계산할 수 있습니다.

자동 교정

자동 보정 또는 자가 보정에서는 먼저 강성을 사용하여 카메라 모션과 파라미터를 복구합니다.그러면 구조를 쉽게 계산할 수 있습니다.이 아이디어를 구현하는 두 가지 방법은 다음과 같습니다.

크루파 방정식

최소 3개의 변위로 강성 ^[7]^[8]구속조건의 기하학적 해석에서 도출된 Kruppa로 ^[6]인한 다항식 시스템을 사용하여 카메라의 내부 매개변수를 얻을 수 있습니다.

$K=AA^{\top }$ K $K=AA^{\top }$ $K=AA^{\top }$ $⊤$ \ $displaystyle$ K $=$ $AA$ $^{\top$ }}: Kruppa 계수 행렬이라는 이름의 Kruppa 방정식에서 알 수 없다.K와 콜레스키 인수분해 방법을 사용하면 고유 매개변수를 쉽게 얻을 수 있습니다.

K=bgin{bmatrix}k_{1}&k_{3}&k_{4}&k_{5}&k_{5}&1\end{bmatrix}

최근에 하틀리는 더 단순한 형태를 제안했다. $(\displaystyle$ F $)$ 를 $F$ F $F=DUV^{\top }$ 로 $F=DUV^{\top }$ 표기합니다 $(\$ F $=DUV^{\top$

그런 다음 Kruppa 방정식이 다시 작성됩니다(파생은 에서 확인할 수 있습니다).

멘돈사와 시폴라

이 방법은 강성 구속조건의 사용에 기초하고 있다.본질적인 모수를 인수로 간주하고 기본 행렬을 모수로 간주하는 비용 함수를 설계합니다. ${F}_{ij}$ 은 $Fi$ j ${Displaystyle$ { $F}$ _ ${F}_{ij}$ {ij ${A}_{i}$ }, ${A}_{j}$ 파라미터행렬은 ${A}_{j}$ ${A}_{i}$ { $style$ ${A}_{j}$ 로 ${A}_{j}$ ${F}_{ij}$ 됩니다.

계층화

최근에는 층화 개념에 기초한 새로운 방법이 ^[10]제안되고 있다.대응으로만 계산할 수 있는 투영 구조에서 시작하여 사용 가능한 모든 제약을 사용하여 이 투영 재구성을 유클리드 재구성으로 업그레이드합니다.이 아이디어로 문제를 다른 섹션으로 계층화할 수 있습니다. 즉, 이용 가능한 제약의 양에 따라 다른 레벨, 투영, 아핀 또는 유클리드 방식으로 분석할 수 있습니다.

3D 지오메트리의 계층화

보통, 세계는 3D 유클리드 공간으로 인식된다.경우에 따라서는 3D 공간의 완전한 유클리드 구조를 사용할 수 없습니다.가장 단순한 사영적인 것은 중간층을 형성하는 아핀 기하학, 그리고 마지막으로 유클리드 기하학입니다.층화의 개념은 기하학적 실체에 대한 일련의 변환과 밀접하게 관련되어 있다: 투영 층은 일련의 투영 변환(호모그래피), 아핀 층은 일련의 아핀 변환, 유클리드 층은 일련의 유클리드 변환이다.

고정 장면이 두 개 이상의 투시 카메라로 캡처되고 서로 다른 영상에서 보이는 점 사이의 대응이 이미 주어졌다고 가정합니다.그러나 실제로 매칭은 컴퓨터 비전에 있어서 매우 중요하고 매우 어려운 문제입니다.여기에서는 $P_{j},j=1,\ldots ,m.$ $P_{j},j=1,\ldots ,m.$ , $P_{j},j=1,\ldots ,m.$ $P_{j},j=1,\ldots ,m.$ 1, $P_{j},j=1,\ldots ,m.$ $.$ {{ $displaystyle$ P_ ${j$ }, j $=1,\ldots,m.}$ 을 $P_{{j}},j=1,\ldots ,m.$ (를) 가진 m{ $displaystyle$ m $}$ $m$ 에서 $m$ $n개의$ 3D $n$ $A_{i}$ $A_{i}$ { $displaystyle A_{i}$ 가 $A_{i}$ $n$ 된다고 가정합니다. $j^{th}$ t $j^{th}$ 이미지의 $i^{th}$ $i^{th}$ h $i^{th}$ i $i^{th}$ $a_{ij}$ $display style$ $a_{$ $ij}$ 만 $a_{ij}$ $i^{th}$ $j^{th}$ $a_{ij}$ 있습니다.

사영 재구성

단순 계산 결과, $(표시$ 스타일 $2nm)$ 의 $2nm$ 독립적인 측정값이 $2nm$ $11m+3n$ $11m+3n$ $(표시$ 스타일 $11m$ + $3n)$ 의 $11m+3n$ 측정값만 알 수 있으므로 충분한 포인트와 이미지로 문제를 해결할 수 있을 것으로 예상됩니다.균질 좌표의 방정식은 다음과 같이 나타낼 수 있습니다.

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

j

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

~

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

,

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

… n

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

,

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

…

a_{ij}\sim P_{j}A_{i}\qquad i=1,\ldots n,~~j=1,\ldots m

{

displaystyle a_{ij}\sim

P_

{i}A_qquad

i

=1, ~j=1,\ldots

m

}

(2)

$P_{j}$ 투영 $(\$ $P_{j}$ $P_{j}H^{-1}$ - 1(\ $displaystyle$ P_ ${j$ $} H^{-1$ }) 및 $P_{j}H^{-1}$ 월드 $A_{i}$ $A_{i}$ i(\ $displaystyle$ A_{ $HA_{i}$ $})$ $A_{i}$ HA $HA_{i}$ i(\ $displaystyle HA_{i$ → HA $HA_{i}$ (\displaystyle HA_{i})에만 비사변환)를 적용할 수 있습니다. 따라서 추가 구속조건은 없습니다.3D 세계입니다.

아핀 재구성

$무한대의$ 위치 계산에 대한 $자세한$ 내용은 아핀스페이스를 참조해 $주세요$ 가장 간단한 방법은 씬(scene)의 선이 평행하거나 점이 다른 두 개의 3분의 1인 정보 등 사전 지식을 활용하는 것입니다.

카메라 모션의 선행 제약도 사용할 수 있습니다.같은 점의 다른 화상을 해석하는 것으로, 운동 방향의 라인을 얻을 수 있다.여러 선의 교차점은 운동 방향의 무한대 지점이며 아핀 구조에 대한 하나의 구속조건입니다.

유클리드 재구성

투영 재구성을 중복 유클리드 제약 조건을 만족시키는 것에 매핑함으로써, 방정식 (2)에서 투영 변환 H를 찾을 수 있다.방정식은 매우 비선형적이므로 구조에 대한 적절한 초기 추측이 필요합니다.이는 선형 투영 - 병렬 투영을 가정하여 얻을 수 있으며, SVD ^[2]분해에 의한 재구성이 용이합니다.

대수적 오차 대 기하학적 오차

필연적으로 측정된 데이터(즉, 이미지 또는 월드 포인트 위치)에 노이즈가 발생하고 노이즈가 여러 소스에서 발생합니다.잡음의 영향을 줄이기 위해 우리는 보통 필요 이상의 방정식을 사용하고 최소 제곱으로 해결합니다.

예를 들어, 일반적인 null-space 문제 공식 Ax = 0(DLT 알고리즘과 마찬가지로)에서 잔차 Ax의 제곱은 최소 제곱법으로 최소화됩니다.

일반적으로 Ax를 기하학적 실체(점, 선, 평면 등) 사이의 거리로 간주할 수 있다면 최소화되는 것은 기하학적 오차이며, 그렇지 않은 경우(오차가 양호한 기하학적 해석이 없을 경우) 대수적 오차라고 합니다.

따라서 대수적 오류와 비교하여 다음과 같은 이유로 기하학적 오류를 최소화하는 것을 선호합니다.

최소화되는 수량에 의미가 있습니다.
솔루션이 더 안정적입니다.
해는 유클리드 변환 하에서 일정하다.

지금까지 살펴본 모든 선형 알고리즘(DLT 및 기타)은 대수적 오류를 최소화합니다.실제로 대수적 오류를 최소화하는 것은 구현의 용이성 외에 선형 문제가 발생하기 때문에 정당성이 없습니다.기하학적 오차의 최소화는 종종 비선형 문제이며, 이는 반복적인 해법만 인정하고 시작점을 필요로 한다.

일반적으로, 대수 잔차에 기초한 선형 해법은 기하학적 비용 함수의 비선형 최소화를 위한 시작점으로 작용하며, 이는 솔루션에 최종 "광택"^[11]을 제공한다.

의료 응용 프로그램

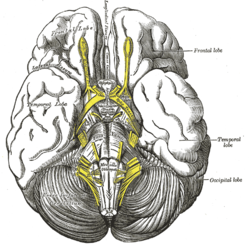
2-D 영상촬영은 해부도가 서로 겹치는 문제가 있어 이상이 드러나지 않습니다.3-D 영상은 진단 및 치료 목적으로 모두 사용할 수 있습니다.

3-D 모델은 수술 계획, 형태측정학 연구에 사용되며 ^[12]정형외과에서 더 높은 신뢰성을 제공합니다.

양쪽 카메라에 P를 투사합니다.

문제의 설명과 기본

카메라가 여러 각도로 촬영한 2-D 영상에서 3-D 영상을 재구성합니다.CT스캔과 MRI와 같은 의료 영상 기술은 비용이 많이 들고 CT스캔은 정확하지만 높은 방사선량을 유도할 수 있어 특정 질병을 앓고 있는 환자에게는 위험이 있다.MRI에 기초한 방법은 정확하지 않습니다.MRI 스캔 시 강력한 자기장에 노출되므로 강자성 금속 임플란트 환자에게는 적합하지 않습니다.두 방법 모두 골격의 전역 구조가 변화하는 누운 위치에서만 수행할 수 있습니다.따라서 선 채로 실행할 수 있는 저방사선량 요건은 다음과 같습니다.

이러한 기법은 3D 영상이지만 관심 영역은 슬라이스로 제한됩니다. 데이터가 수집되어 시간 시퀀스를 형성합니다.

스테레오 대응점 기반 기술

이 방법은 간단하며 멀티 뷰 방사선 사진에서 수동으로 포인트를 식별하여 구현됩니다.첫 번째 단계는 두 개의 X선 영상에서 해당 지점을 추출하는 것입니다.두 번째 단계는 이산 선형 변환(^[13]DLT)과 같은 알고리즘을 사용하여 영상을 3차원으로 재구성하는 것입니다.재구성은 SCP(스테레오 대응 포인트)가 있는 경우에만 가능합니다.결과의 품질은 SCP의 양에 따라 달라집니다.SCP가 많을수록 결과는 좋아지지만 느리고 부정확합니다.오퍼레이터의 스킬은 이미지 품질에 영향을 미칩니다.SCP 기반 기법은 식별 가능한 가장자리가 없는 골격 구조에는 적합하지 않습니다.일반적으로 SCP 기반 기술은 다른 ^[15]방법을 포함하는 프로세스의 일부로 사용됩니다.

비스테레오 대응 등고선법(NCSS)

이 방법은 3D 재구성에 X선 영상을 사용하고 무게 지지 위치에서 저선량 방사선의 3D 모델을 개발합니다.

NSCC 알고리즘에서는 첫 번째 단계는 초기 솔루션의 계산입니다.먼저 일반 객체의 해부학적 영역이 정의됩니다.둘째, 방사선 사진에 대한 수동 2D 윤곽선 식별이 수행됩니다.각 방사선 사진으로부터 3D 초기 용액 객체를 사용해 2D 윤곽을 생성한다.초기 물체 표면의 3D 윤곽이 관련 방사선 ^[15]사진에 투영된다.이 두 설정 지점 간에 수행되는 2D 연결은 2D 등고선과 3D 등고선 간의 대응 관계를 개발하는 지점 간 거리와 등고선 도출을 기반으로 합니다.다음 단계는 초기 솔루션의 최적화입니다.마지막으로 최적화된 ^[16]솔루션의 변형은 최적화된 솔루션에 Kriging 알고리즘을 적용하여 이루어집니다.마지막으로 2개의 설정점 사이의 거리가 소정의 정밀도 값보다 클 때까지 마지막 단계를 반복함으로써 재구성 대상물을 얻는다.

이 방법의 장점은 연속적인 형태를 가진 골격 구조에 사용될 수 있고 인간의 개입도 줄었지만 시간이 많이 걸린다는 것입니다.

표면 렌더링 기술

지표면 렌더링에서는 3D 객체를 iso-surfaces라고 하는 지표면 세트로 시각화합니다.각 표면에는 강도가 동일한 점(iso-값이라고 함)이 있습니다.이 기술은 일반적으로 고대비 데이터에 적용되며 분리된 구조를 설명하는 데 도움이 됩니다. 예를 들어, 두개골은 머리의 슬라이스에서 생성되거나 혈관 시스템은 몸의 슬라이스에서 생성될 수 있습니다.주로 다음 두 가지 방법이 있습니다.

등고선 기반 재구성:iso-contours가 서로 붙어 iso-surface를 ^[17]형성합니다.
Voxel(복셀) 기반 재구성: 동일한 강도 값의 복셀을 사용하여 Iso-Surface(iso-surface)를 형성합니다.인기 있는 알고리즘은 행진 큐브, 행진 4면체, 분할 ^[17]큐브입니다.

다른 방법에서는 통계적 형상 모형, 모수 또는 두 가지 유형의 하이브리드를 사용합니다.

「」를 참조해 주세요.

3D 포즈 추정 – 물체의 공간적 특성을 결정하는 과정
3D 재구성 – 실제 물체의 모양과 외관을 포착하는 프로세스
3D 사진
2D에서 3D로 변환– 2D 필름을 3D 형태로 변환하는 프로세스
3D 데이터 수집 및 객체 재구성
에피폴라 지오메트리– 스테레오 비전의 지오메트리
카메라의 재설치
컴퓨터 스테레오 비전 – 디지털 이미지에서 3D 데이터 추출
움직임으로부터의 구조 – 움직이는 물체로부터 3D를 재구성하는 방법
사진 측량 소프트웨어 비교
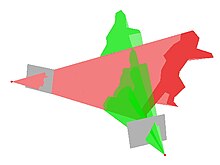
육안 선체
인체 이미지 합성 – 컴퓨터 생성 인체 이미지

레퍼런스

^ "Soltani, A. A., Huang, H., Wu, J., Kulkarni, T. D., & Tenenbaum, J. B. Synthesizing 3D Shapes via Modeling Multi-View Depth Maps and Silhouettes With Deep Generative Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1511-1519)". 6 March 2020.
^ ^a ^b C. Tomasi와 T. Kanade, "정자법에 따른 이미지 스트림의 형태와 움직임: 인수분해 접근법", 국제 컴퓨터 비전 저널, 9(2):137-154, 1992.
^ A. Laurentini (February 1994). "The visual hull concept for silhouette-based image understanding". IEEE Transactions on Pattern Analysis and Machine Intelligence. 16 (2): 150–162. doi:10.1109/34.273735.
^ R. Mohr와 E.아보가스트카메라 보정 없이도 가능합니다.패턴 인식 서신, 12:39-43, 1991.
^ 오, 파우제라스보정되지 않은 스테레오 리그를 사용하면 3차원으로 무엇을 볼 수 있습니까?유럽 컴퓨터 비전 회의의 진행, 563-578페이지, 산타 마르게리타 L., 1992.
^ E. 크루파Zur Ermittlung eines Objektes aus zwei Perspektiven mit inner Orientierung.앉아-베르아카드, 위스, 빈, 수학, 내추럴아방 IIa, 122:1939-1948, 1913
^ S. J. 메이뱅크와 O.파우제라스.움직이는 카메라의 자기 보정 이론입니다.International Journal of Computer Vision, 8(2): 123-151, 1992.
^ O. Paugeras와 S.메이뱅크.시점부터의 움직임 일치: 다양한 솔루션.International Journal of Computer Vision, 4(3): 225-246, 1990년 6월
^ ^a ^b R. I. 하틀리크루파의 방정식은 기본행렬에서 파생되었다.패턴 분석 및 머신 인텔리전스에 관한 IEEE 트랜잭션, 19(2): 133-135, 1997년 2월.
^ 폴리스, 마크보정되지 않은 영상^{[dead link]} 시퀀스에서 자가 보정 및 메트릭 3D 재구성.디스 박사 논문, ESAT-PSI, KU Leuben, 1999.
^ R. 하틀리와 A.지저맨.컴퓨터 비전의 다중 뷰 지오메트리.케임브리지 대학 출판부, 제2판, 2003년.
^ "Medical Visualization: What is it and what's it for?". GarageFarm. 2018-02-18. Retrieved 2018-02-18.
^ "Pearcy MJ. 1985. Stereo radiography of lumbar spine motion. Acta Orthop Scand Suppl".
^ "Aubin CE, Dansereau J, Parent F, Labelle H, de Guise JA. 1997. Morphometric evaluations of personalised 3D reconstructions and geometric models of the human spine". Med Biol Eng Comput.
^ ^a ^b "S.Hosseinian, H.Arefi, 3D Reconstruction from multiview medical X-ray images- Review and evaluation of existing methods" (PDF).
^ Laporte, S; Skalli, W; de Guise, JA; Lavaste, F; Mitton, D (2003). "A biplanar reconstruction method based on 2D and 3D contours: application to distal femur". Comput Methods Biomech Biomed Engin. 6 (1): 1–6. doi:10.1080/1025584031000065956. PMID 12623432. S2CID 3206752.
^ ^a ^b G.Scott Owen, HyperVis. ACM SIGGRAPH Education Committee, the National Science Foundation (DUE-9752398), and the Hypermedia and Visualization Laboratory, Georgia State University.

추가 정보

후루카와 야스타카와 카를로스 에르난데스(2015) 멀티뷰 스테레오 : A 튜토리얼 [1]
플린, 존 등"Deepstereo: 세계의 이미지에서 새로운 시각을 예측하는 법을 배우고 있습니다."컴퓨터 비전과 패턴 인식에 관한 IEEE 회의의 진행 상황. 2016년.

외부 링크

여러 영상에서 3D 재구성 - 일반 영상에서 3D 모델을 추출하는 방법에 대해 설명합니다.
이미지 및 비디오에서 시각적인 3D 모델링 - 이미지 및 비디오에서 3D 재구성에 대한 이론, 실습 및 요령을 설명하는 기술 보고서입니다.
다중 뷰 깊이 맵 및 심층 생성 네트워크를 통한 실루엣 모델링을 통한 3D 모양 합성 - 다중 뷰 깊이 맵 또는 실루엣 모델링을 통해 3D 모양을 생성하고 재구성할 수 있습니다.

[3DVAE-1] "Soltani, A. A., Huang, H., Wu, J., Kulkarni, T. D., & Tenenbaum, J. B. Synthesizing 3D Shapes via Modeling Multi-View Depth Maps and Silhouettes With Deep Generative Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1511-1519)". 6 March 2020.

[Tomasi-2] C. Tomasi와 T. Kanade, "정자법에 따른 이미지 스트림의 형태와 움직임: 인수분해 접근법", 국제 컴퓨터 비전 저널, 9(2):137-154, 1992.

[LaurentiniVisualHull-3] A. Laurentini (February 1994). "The visual hull concept for silhouette-based image understanding". IEEE Transactions on Pattern Analysis and Machine Intelligence. 16 (2): 150–162. doi:10.1109/34.273735.

[4] R. Mohr와 E.아보가스트카메라 보정 없이도 가능합니다.패턴 인식 서신, 12:39-43, 1991.

[5] 오, 파우제라스보정되지 않은 스테레오 리그를 사용하면 3차원으로 무엇을 볼 수 있습니까?유럽 컴퓨터 비전 회의의 진행, 563-578페이지, 산타 마르게리타 L., 1992.

[6] E. 크루파Zur Ermittlung eines Objektes aus zwei Perspektiven mit inner Orientierung.앉아-베르아카드, 위스, 빈, 수학, 내추럴아방 IIa, 122:1939-1948, 1913

[7] S. J. 메이뱅크와 O.파우제라스.움직이는 카메라의 자기 보정 이론입니다.International Journal of Computer Vision, 8(2): 123-151, 1992.

[8] O. Paugeras와 S.메이뱅크.시점부터의 움직임 일치: 다양한 솔루션.International Journal of Computer Vision, 4(3): 225-246, 1990년 6월

[Hartley-9] R. I. 하틀리크루파의 방정식은 기본행렬에서 파생되었다.패턴 분석 및 머신 인텔리전스에 관한 IEEE 트랜잭션, 19(2): 133-135, 1997년 2월.

[10] 폴리스, 마크보정되지 않은 영상^{[dead link]} 시퀀스에서 자가 보정 및 메트릭 3D 재구성.디스 박사 논문, ESAT-PSI, KU Leuben, 1999.

[11] R. 하틀리와 A.지저맨.컴퓨터 비전의 다중 뷰 지오메트리.케임브리지 대학 출판부, 제2판, 2003년.

[12] "Medical Visualization: What is it and what's it for?". GarageFarm. 2018-02-18. Retrieved 2018-02-18.

[13] "Pearcy MJ. 1985. Stereo radiography of lumbar spine motion. Acta Orthop Scand Suppl".

[14] "Aubin CE, Dansereau J, Parent F, Labelle H, de Guise JA. 1997. Morphometric evaluations of personalised 3D reconstructions and geometric models of the human spine". Med Biol Eng Comput.

[:0-15] "S.Hosseinian, H.Arefi, 3D Reconstruction from multiview medical X-ray images- Review and evaluation of existing methods" (PDF).

[16] Laporte, S; Skalli, W; de Guise, JA; Lavaste, F; Mitton, D (2003). "A biplanar reconstruction method based on 2D and 3D contours: application to distal femur". Comput Methods Biomech Biomed Engin. 6 (1): 1–6. doi:10.1080/1025584031000065956. PMID 12623432. S2CID 3206752.

[:1-17] G.Scott Owen, HyperVis. ACM SIGGRAPH Education Committee, the National Science Foundation (DUE-9752398), and the Hypermedia and Visualization Laboratory, Georgia State University.

[2]

[3]

[4]

[5]

[7]

[8]

[6]

[10]

[11]

[12]

[13]

[15]

[16]

[17]

Search

여러 영상에서 3D 재구성

네임스페이스

더

목차

처리.

재건에 대한 수학적 설명