투영-슬라이스 정리
Projection-slice theorem수학에서 투영-슬라이스 정리, 중앙 슬라이스 정리 또는 푸리에 슬라이스 정리는 다음과 같은 두 가지 계산의 결과가 동일하다고 명시한다.
- 2차원 함수 f(r)를 사용하여 (예를 들어 라돈 변환을 사용하여) 선에 투영한 후, 그 투영을 푸리에 변환한다.
- 같은 기능을 취하되 먼저 2차원 푸리에 변환을 한 다음 투영선과 평행한 원점을 잘라내라.
연산자 용어로, 다음과 같은 경우
- F와1 F는2 위에서 언급한 1차원 푸리에 변환 연산자 입니다.
- P는1 투영 연산자(1-D 라인에 2-D 함수를 투영하는 연산자)이다.
- S는1 슬라이스 연산자(함수에서 1-D 중심 슬라이스를 추출한다)
그때
이 아이디어는 더 높은 차원으로 확장될 수 있다.
예를 들어 의료용 CT 스캔 분석에서 "투영"이 내부 장기의 X선 영상인 경우 이 정리가 사용된다.이러한 영상의 푸리에 변환은 내부 장기의 3차원 밀도의 푸리에 변환을 통해 슬라이스로 보여지며, 이러한 슬라이스를 보간하여 그 밀도의 완전한 푸리에 변환을 구축할 수 있다.역 푸리에 변환은 물체의 3차원 밀도를 회복하는 데 사용된다.이 기술은 1956년 로널드 N. 브레이스웰에 의해 전파추출 문제로 처음 파생되었다.[1]
N차원의 투영-슬라이스 정리
N 치수에서 투영-슬라이스 정리는 N-차원 함수 f(r)의 투영을 m-차원 선형 서브매니폴드에 대한 푸리에 변환은 푸리에 sp의 원점을 통해 m-차원 선형 서브매니폴드로 구성된 해당 함수의 N-차원 푸리에 변환의 m-차원 슬라이스와 동일하다고 명시한다.서브매니폴드와 평행한 에이스.측정 시스템 용어:
일반화된 푸리에-슬라이스 정리
N차원으로 일반화하는 것 외에, 투영-슬라이스 정리는 임의의 근거 변경으로 더욱 일반화될 수 있다.[2]표기법의 편리성을 위해, N차원 열 벡터에서 동작하는 N-by-N 변위성 행렬인 B로 표기하는 것을 고려한다.그렇다면 일반화된 푸리에-슬라이스 정리는 다음과 같이 말할 수 있다.
여기서 - =( - ) 은 기본 변환의 변화 역의 전치물이다.
2차원의 증거
투영-슬라이스 정리는 2차원의 경우에 쉽게 증명된다.일반성을 잃지 않고 투영선을 X축으로 가져갈 수 있다.시프트와 회전선을 사용해도 여전히 법이 적용되기 때문에 일반성의 손실은 없다.이동된 선(y)을 사용하면 동일한 투영 결과를 얻을 수 있으므로 동일한 1D 푸리에 변환 결과를 얻을 수 있다.회전함수는 회전이 된 푸리에 변환의 푸리에 쌍으로, 정리가 다시 이를 지탱한다.
f(x, y)가 2차원 함수인 경우, x축에 대한 f(x, y)의 투영은 p(x)이다.
( , ) 의 푸리에 변환은
그런 다음 슬라이스가 ) s인 경우
그것은 p(x)의 푸리에 변환일 뿐이다.보다 높은 차원에 대한 증거는 위의 예로부터 쉽게 일반화된다.
FHA 사이클
2차원 함수 f(r)가 원형 대칭인 경우 f(r)로 나타낼 수 있다. 여기서 r = r. 이 경우 투영 라인에 대한 투영은 f(r)의 아벨 변환이 된다.f(r)의 2차원 푸리에 변환은 f(r)의 zerot-order Hankel 변환에 의해 주어진 원형 대칭함수가 될 것이며, 따라서 원점을 통과하는 어떤 조각도 나타낼 것이다.그런 다음 투영-슬라이스 정리는 투영의 푸리에 변환이 슬라이스와 동일하다고 명시한다.
여기서 A는1 아벨 변환 연산자를 나타내며, 2차원 원형 대칭함수를 1차원 선에 투영하고, F는1 1-D 푸리에 변환 연산자를 나타내며, H는 제로-오더 행클 변환 연산자를 나타낸다.
팬 빔 또는 콘 빔 CT로 확장
투영-슬라이스 정리는 병렬 빔 투영을 통한 CT 영상 재구성에 적합하다.팬빔이나 콘빔 CT에는 직접 적용하지 않는다.1995년 솽렌 자오에 의해 팬빔과 콘빔 CT 영상 재구성으로 정리가 확대되었다.[3]
참고 항목
참조
- ^ Bracewell, Ronald N. (1956). "Strip integration in radio astronomy". Australian Journal of Physics. 9 (2): 198–217. Bibcode:1956AuJPh...9..198B. doi:10.1071/PH560198.
- ^ Ng, Ren (2005). "Fourier Slice Photography" (PDF). ACM Transactions on Graphics. 24 (3): 735–744. doi:10.1145/1073204.1073256.
- ^ Zhao S.R. and H.Halling (1995). A New Fourier Transform Method for fan Beam Tomography. Published in 1995 Nuclear Science Symposium and Medical Imaging Conference Record. Vol. 2. pp. 1287–91. doi:10.1109/NSSMIC.1995.510494. ISBN 978-0-7803-3180-8. S2CID 60933220.
추가 읽기
- Bracewell, Ronald N. (1990). "Numerical Transforms". Science. 248 (4956): 697–704. Bibcode:1990Sci...248..697B. doi:10.1126/science.248.4956.697. PMID 17812072. S2CID 5643835.
- Bracewell, Ronald N. (1956). "Strip Integration in Radio Astronomy". Aust. J. Phys. 9 (2): 198. Bibcode:1956AuJPh...9..198B. doi:10.1071/PH560198.
- Gaskill, Jack D. (2005). Linear Systems, Fourier Transforms, and Optics. John Wiley & Sons, New York. ISBN 978-0-471-29288-3.
- Ng, Ren (2005). "Fourier Slice Photography" (PDF). ACM Transactions on Graphics. 24 (3): 735–744. doi:10.1145/1073204.1073256.
- Zhao, Shuang-Ren; Halling, Horst (1995). "Reconstruction of Cone Beam Projections with Free Source Path by a Generalized Fourier Method". Proceedings of the 1995 International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine: 323–7.
- Garces, Daissy H.; Rhodes, William T.; Peña, Néstor (2011). "The Projection-Slice Theorem: A Compact Notation". Journal of the Optical Society of America A. 28 (5): 766–769. Bibcode:2011JOSAA..28..766G. doi:10.1364/JOSAA.28.000766. PMID 21532686.
외부 링크
- Fourier Slice Theorem (video). Part of the "Computed Tomography and the ASTRA Toolbox" course. University of Antwerp. September 10, 2015.




 기본 변환의 변화 역의 전치물이다.
기본 변환의 변화 역의 전치물이다. 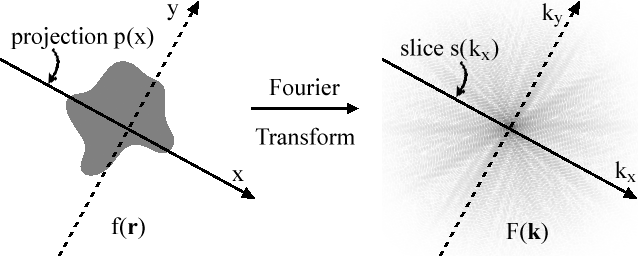




![=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d83ac57cdc5698f37cff3d7535c27bd32fef52)




