허셜 그래프

Herschel graph
허셜 그래프
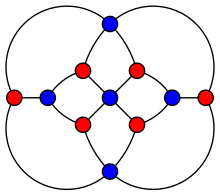Herschel graph LS.svg
허셜 그래프.
의 이름을 따서 명명됨알렉산더 스튜어트 허셜
꼭지점11
가장자리18
반지름3
직경4
둘레4
자기동형12 (D6)
색수2
색채 지수4
특성.다면체
평면
초당파
완벽하다
그래프 및 매개 변수 표

수학의 한 분야인 그래프 이론에서 허셜 그래프는 11개의 꼭지점과 18개의 모서리를 가진 양방향 무방향 그래프입니다.이것은 다면체 그래프(볼록 다면체의 그래프)이며, 모든 정점을 통과하는 주기인 해밀턴 주기를 가지지 않는 가장 작은 다면체 그래프입니다.이것은 영국 천문학자 알렉산더 스튜어트 허셜의 이름을 따서 지어졌는데, 이는 허셜이 다면체 그래프에서 해밀턴 주기를 연구했기 때문이다.

정의 및 속성

허셜 그래프에는 4도 정점 3개와 3도 정점 8개가 있습니다.세 쌍의 4도 정점은 각각 4개의 정점으로 이루어진 사이클을 형성하며, 3도 정점 중 2개와 번갈아 이루어집니다.나머지 2개의 도수 3개의 정점은 이들 3개의 사이클 각각에서 도수 3개의 정점에 인접해 있다.

허셜 그래프는 평면 그래프입니다. 모서리가 교차하지 않고 평면에 그릴 수 있습니다.또한 3개의 버텍스로 연결되어 있어 두 개의 꼭지점을 제거하면 연결된 하위 그래프가 남습니다.이것은 초당 그래프입니다. 정점은 각각 5개의 정점과 6개의 정점으로 이루어진 2개의 서브셋으로 분리할 수 있으며, 따라서 모든 엣지는 각 서브셋에 끝점을 가질 수 있습니다(그림의 빨간색 및 파란색 서브셋).다른 초당 그래프와 마찬가지로, 허셜 그래프는 완벽한 그래프입니다. 유도된 모든 하위 그래프의 색 숫자는 해당 하위 그래프의 가장 큰 그룹 크기와 같습니다.또한 색도 지수 4, 둘레 4, 반지름 3, 지름 4를 가지고 있다.

다면체

다면체로서의 허셜 그래프.[1]애니메이션 버전을 보려면 여기를 클릭하십시오.

허셜 그래프는 평면적이고 3개의 버텍스로 연결되어 있기 때문에 슈타이니츠의 정리에 따라 다면체 그래프입니다: 허셜 그래프를 골격으로 [2]하는 볼록 다면체(무호흡면체)가 존재합니다.이 다면체는 면의 사변형 9개를 가지고 있으며, 3개의 마름모꼴과 [1]6개의 연을 형성하기 위해 선택할 수 있다.

그것의 이중 다면체는 삼각형 프리즘의 모서리 중간점의 볼록한 선체로 형성된 정류된 삼각형 프리즘이다.이 다면체는 연속된 번호가 인접한 면에 나타나도록 면의 번호를 매길 수 없고, 첫 번째와 마지막 번호가 인접한 면에 있는 특성을 가지고 있습니다.이러한 유형의 다면체 얼굴 번호는 Magic 게임에서는 "spindown life counters"로 사용되므로 다음과 같습니다. Gathering, Constantinides & Constantinides (2018)는 이 이중 다면체의 표준 다면체 실현을 "Lich's nemesis"[3]라고 명명했다.

해밀턴성

허셜 그래프의 해밀턴 경로(사이클이 아님)

홀수 개의 정점을 갖는 초당 그래프로서, 허셜 그래프에는 해밀턴 주기(각 정점을 정확히 한 번 통과하는 가장자리 주기)가 포함되어 있지 않습니다.어떤 초당 그래프에서든, 모든 주기는 초당 양쪽에 있는 정점들 사이를 번갈아 가야 하기 때문에, 양쪽 정점의 동일한 수를 포함해야 하며, 짝수 길이를 가져야 합니다.따라서, 11개의 꼭지점 각각을 한 번 통과하는 주기는 허셜 그래프에 존재할 수 없습니다.그래프의 크기가 정점, 모서리 또는 [4]면의 수로 측정되는지 여부에 관계없이 가장 작은 비 해밀턴 다면체 그래프입니다.정점이 11개이고 해밀턴 사이클이 없는 다른 다면체 그래프(특히 골드너-해리 그래프[5])가 있지만 [2]모서리가 적은 그래프는 없다.

허셜 그래프의 꼭지점 세 개를 제외한 모든 것은 3도를 가집니다.Tait의[6] 추측은 모든 정점이 3도를 갖는 다면체 그래프는 해밀턴식이어야 한다고 말하지만, 이것은 W. T. Tutte가 훨씬 더 큰 반례를 제시했을 때 반증되었다.[7]모든 초당 3정규 다면체 그래프가 해밀턴이라는 바네트의 추측인 Tait의 추측의 개선은 여전히 [8]열려 있다.

해밀턴 주기가 없는 모든 최대 평면 그래프에는 마이너로 허셜 그래프가 있습니다.허셜 그래프는 세 개의 작은 최소 비 해밀턴 3-vertex 연결 그래프 중 하나로 추측된다.나머지 두 가지는 완전한 초당 3, K_와 Herschel 와 ,4(4})를 모두 3개의 버텍스 구분자로 두 개의 대칭 반으로 나눈 다음 [9]각 그래프에서 절반씩 합친 그래프입니다.

허셜 그래프의 중앙 그래프는 해밀턴 분해가 없는 4정규 평면 그래프입니다.음영 영역은 기본 허셜 그래프의 정점에 해당합니다.

허셜 그래프는 또한 중앙 그래프를 두 개의 에지-분리 해밀턴 사이클로 분해할 수 없는 다면체 그래프의 예를 제공합니다.허셜 그래프의 중앙 그래프는 허셜 그래프의 각 모서리에 하나씩 18개의 정점이 있는 4개의 규칙 그래프입니다. 허셜 그래프의 해당 모서리가 한 [10]면에 연속될 때마다 두 개의 정점이 중앙 그래프에 인접합니다.이는 4-vertex 연결 및 기본적으로 6-edge 연결입니다. 즉, 두 개 이상의 정점으로 이루어진 두 개의 하위 집합으로 정점의 모든 분할에 대해 분할된 최소 6개의 가장자리가 해당 [11]분할과 교차합니다.

역사

허셜 그래프는 윌리엄 로완 해밀턴의 아이코시안 게임에 관한 초기 논문을 쓴 영국 천문학자 알렉산더 스튜어트 허셜의 이름을 따왔다: 허셜 그래프는 이 게임이 해답이 없는 가장 작은 볼록 다면체를 묘사한다.그러나 허셜의 논문은 아이코시안 게임에 대한 해법을 정사면체와 정이십면체의 그래프에만 기술하고 허셜 [12]그래프는 기술하지 않았다."[13]허셜 그래프"라는 이름은 1976년에 출판된 존 아드리안 본디와 U.S. R. 머티가 쓴 그래프 이론 교과서에 일찍 등장했습니다.그러나 그래프 자체는 예를 들어 H. S. M. Coxeter에 [2]의해 이전에 설명되었다.

레퍼런스

  1. ^ a b Lawson-Perfect, Christian (13 October 2013), "An enneahedron for Herschel", The Aperiodical, retrieved 7 December 2016
  2. ^ a b c 를 클릭합니다Coxeter, H. S. M. (1973), Regular Polytopes, Dover, p. 8.
  3. ^ Constantinides, Anthony F.; Constantinides, George A. (October 2018), "Spindown Polyhedra", The Mathematical Gazette, 102 (555): 447–453, doi:10.1017/mag.2018.111
  4. ^ 를 클릭합니다Barnette, David; Jucovič, Ernest (1970), "Hamiltonian circuits on 3-polytopes", Journal of Combinatorial Theory, 9 (1): 54–59, doi:10.1016/S0021-9800(70)80054-0.
  5. ^ 를 클릭합니다Weisstein, Eric W., "Goldner-Harary Graph", MathWorld.
  6. ^ 사이언티픽 페이퍼, Vol.에 전재Tait, P. G. (1884), "Listing's Topologie", Philosophical Magazine, 5th Series, 17: 30–46.II, 페이지 85-98.
  7. ^ 를 클릭합니다Tutte, W. T. (1946), "On Hamiltonian circuits" (PDF), Journal of the London Mathematical Society, 21 (2): 98–101, doi:10.1112/jlms/s1-21.2.98[dead link].
  8. ^ Samal, Robert (11 June 2007), Barnette's conjecture, the Open Problem Garden, retrieved 24 Feb 2011
  9. ^ Ding, Guoli; Marshall, Emily (2018), "Minimal -connected non-Hamiltonian graphs", Graphs and Combinatorics, 34 (2): 289–312, doi:10.1007/s00373-018-1874-z, MR 3774453
  10. ^ 를 클릭합니다Bondy, J. A.; Häggkvist, R. (1981), "Edge-disjoint Hamilton cycles in 4-regular planar graphs", Aequationes Mathematicae, 22 (1): 42–45, doi:10.1007/BF02190157.
  11. ^ Király, Csaba; Péterfalvi, Ferenc (2012), "Balanced generic circuits without long paths", Discrete Mathematics, 312 (15): 2262–2271, doi:10.1016/j.disc.2012.03.031, MR 2926099
  12. ^ 를 클릭합니다Herschel, A. S. (1862), "Sir Wm. Hamilton's Icosian Game", The Quarterly Journal of Pure and Applied Mathematics, 5: 305.
  13. ^ Bondy, J. A.; Murty, U. S. R. (1976), Graph Theory With Applications, North Holland, p. 53, MR 0411988

외부 링크

Wikimedia Commons는 허셜 그래프와 관련된 미디어를 가지고 있습니다.