투테 그래프

투테 그래프
투테 그래프
이름을 따서 명명됨	W. T. 투테
정점	46
가장자리	69
반지름	5
지름	8
둘레	4
자동형성	3(Z/3Z)
색수	3
색도 지수	3
특성.	큐빅 플라나르 다면체
그래프 및 모수 표

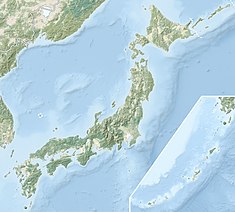
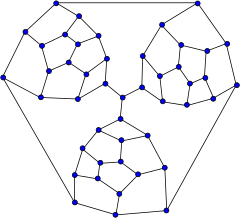
그래프 이론의 수학적 분야에서 투테 그래프는 46개의 정점과 69개의 가장자리의 W. T. 투테의 이름을 딴 3-정규 그래프다.^[1]색도 번호 3, 색도 지수 3, 둘레 4, 지름 8을 가지고 있다.

투트 그래프는 입방체 다면체 그래프지만 해밀턴식 그래프는 아니다.따라서, 3개의 규칙적인 다면체마다 해밀턴 사이클이 있다는 것은 타이트의 추측에 대한 백례다.^[2]

1946년 투테에 의해 출판된 이 책은 이 추측을 위해 만들어진 최초의 백작이다.^[3]다른 백배추들도 나중에 발견되었는데, 많은 경우 그리그버그의 정리를 바탕으로 한 것이었다.

건설

투트 조각이라고 불리는 작은 평면 그래프로, W. T. 투트는 해밀턴이 아닌 다면체를 세 개의 파편을 합쳐서 만들었다.파편을 통과하는 해밀턴 경로의 일부여야 하는 파편의 "강제" 가장자리는 중앙 꼭지점에 연결된다. 어떤 사이클이든 이 세 에지 중 2개만 사용할 수 있기 때문에 해밀턴 사이클은 있을 수 없다.

결과 그래프는 3개의 연결과 평면이기 때문에 슈타이니츠의 정리로는 다면체의 그래프다.그것은 25개의 얼굴을 가지고 있다.

4면체(도면에 있는 4개의 큰 9면체 면에 해당하며, 그 중 3면은 조각의 쌍 사이에 있고 4번째는 외부를 형성하는 면에 해당함)에서 정점 세 개를 곱하여 기하학적으로 실현할 수 있다.

대수적 특성

Tutte 그래프의 자동형성 그룹은 순서 3의 순환형 그룹인 Z/3Z이다.

Tutte 그래프의 특성 다항식은 다음과 같다.

${\displaystyle (x-3)(x^{15}-22x^{13}+x^{12}+184x^{11}-26x^{10}-731x^{9}+199x^{8}+1383x^{7}-576x^{6}-1061x^{5}+561x^{4}+233x^{3}-151x^{2}+4x+4)^{2}}$

${\displaystyle (x^{15}+3x^{14}-16x^{13}-50x^{12}+94x^{11}+310x^{10}-257x^{9}-893x^{8}+366x^{7}+1218x^{6}-347x^{5}-717x^{4}+236x^{3}+128x^{2}-56x+4).}$

관련 그래프

투테 그래프가 최초로 발견된 3정규 비 해밀턴 다면 그래프지만, 그런 그래프 중 가장 작은 것은 아니다.

1965년 레더버그는 38개의 꼭지점에서 바넷-보사크-레더버그 그래프를 발견했다.^[4][5]1968년에 그린버그는 타이트의 추측에 대한 추가적인 작은 백배수 즉 42, 44, 46 정점에 그린버그 그래프를 만들었다.^[6]1974년 Faulkner와 Lounger는 두 개의 그래프를 더 출판했다 - Faulkner–42와 44 정점에 대한 젊은 그래프.^[7]

마침내 홀튼과 맥케이는 해밀턴이 아닌 6개의 38-Vertex 비-해밀턴 다면체가 있다는 것을 보여주었다.그것들은 투트의 예에서 사용된 것과 같은 파편으로 오각형 프리즘의 두 정점을 대체함으로써 형성된다.^[8]

참조