에바인센트 필드

금속-유전성 인터페이스를 따라 전파되는 표면파(표면 플라스몬 폴라티톤)의 도식적 표현.표면에서 떨어져 있는 필드는 기하급수적으로 소멸되며(우측 그래프) 이러한 필드는 z 방향으로 반사되는 것으로 설명된다.

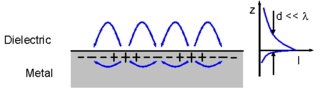
전자기학에서 전계장 또는 전계파는 전자기파로 전파되지 않고 에너지가 소스(전하 및 전류) 근처에 공간적으로 집중되는 진동하는 전기장 및/또는 자기장이다.전파 전자파가 생성되는 경우에도(예: 송신 안테나에 의해) 많은 파장에서 관측되는 전파 파장에 귀속될 수 없는 전기장 또는 자기장의 구성요소를 전파장(전송 안테나의 원장 등)으로 식별할 수 있다.

발생장치의 특징은 그 지역에 순에너지 흐름이 없다는 것이다.전자기 에너지의 순흐름은 평균 포아닌팅 벡터에 의해 주어지기 때문에, 이는 완전한 진동 사이클에 걸쳐 평균적으로 이들 지역의 포아닌팅 벡터가 0이라는 것을 의미한다.^[a]

용어의 사용

많은 경우에, 어떤 분야가 단순히 발생하거나 발생하지 않는다고 말할 수 없다.예를 들어 위의 그림에서 에너지는 실제로 수평 방향으로 전달된다.전계 강도는 표면에서 기하급수적으로 떨어져서 인터페이스에 매우 가까운 지역에 집중하게 되는데, 그 때문에 이것을 표면파라고 한다.^[1]그러나 (z 방향에서) 표면으로부터 (또는) 떨어져 있는 에너지의 전파는 없으므로, 필드를 "z 방향으로 진화하는" 것으로 적절히 설명할 수 있다.이것은 그 용어의 부정확함을 보여주는 하나의 예다.그것들이 존재하는 대부분의 경우, 발산성 특성(한 방향 또는 모든 방향에서 0의 평균 포나이팅 벡터)이 지적되지 않고, 단순히 전기장 또는 자기장으로 생각되고 일컬어진다.이 용어는 일반적으로 전파파를 예상하는 경우에서 현장 또는 솔루션을 구별하기 위해 특히 사용된다.

일상적인 전자기기와 전기기기는 이 성질을 가진 넓은 들판으로 둘러싸여 있다.그들의 작동은 교류 전압(그들 사이에서 전기장을 생성)과 교류(그들 주위의 자기장을 생성)를 포함한다."발광"이라는 용어는 이런 평범한 맥락에서 결코 들을 수 없다.오히려 전파 전자파의 우발적인 생산과 그에 따라 (전파파가 회로로부터 전력을 빼앗아 가기 때문에) 방사선 손실을 줄이는 것에 대한 논의 또는 간섭에 대한 우려가 있을 수 있다.한편, "발광장"은 그러한 특성이 없는 수반되는 전자기 구성요소를 설명하기 위해 (제한된 경우에도) 전파 전자파가 관련된 다양한 맥락에서 사용된다.또는 일반적으로 전자기파(유리와 공기 사이의 인터페이스에서 굴절되는 빛과 같은)가 있는 경우에 해당 파동이 억제될 때(예를 들어 임계 각도를 넘는 무선 인터페이스에서 유리 입사 광선)를 필드라고 설명하기 위해 이 용어가 호출된다.

모든 전자기장은 맥스웰 방정식에 따라 분류적으로 관리되지만, 서로 다른 기술이나 문제에는 특정 유형의 예상 해결책이 있으며, 일차 해결책이 파동 전파와 관련된 경우, "발광"이라는 용어는 그 속성을 공유하지 않는 필드 구성요소나 솔루션에 자주 적용된다.예를 들어 중공 금속 도파관의 전파 상수는 주파수의 강력한 함수(일명 분산 관계)이다.특정 주파수(차단 주파수) 이하에서는 전파 상수가 가상의 숫자가 된다.상상 수명을 갖는 파동 방정식에 대한 해결책은 파동으로 전파되지 않고 기하급수적으로 떨어지기 때문에 그 낮은 주파수에서 흥분되는 장은 발산하는 것으로 간주된다.또한 단순히 그 주파수에 대해 전파는 "허용되지 않는다"고 말할 수 있다.파동 방정식에 대한 공식 해법은 동일한 형태를 갖는 모드를 설명할 수 있지만, 주파수가 컷오프 주파수 아래로 떨어짐에 따라 실제에서 가상으로 전파 상수가 변하는 것은 결과의 물리적 특성을 완전히 변화시킨다.해결책은 "차단 모드" 또는 "발진 모드"^[2]^[3]^{: 360}로 설명될 수 있지만, 다른 저자는 그러한 모드가 존재하지 않는다고 명시할 것이다.모드에 해당하는 발생장치는 파동 방정식의 해결책으로 계산되었기 때문에 그 성질(에너지를 운반하지 않는 등)이 파동의 정의와 일치하지 않더라도 흔히 "발진파"라고 논한다.

이 논문은 전자기학에 초점을 맞추고 있지만, 전파방정식이 관련 물리학에서 발생하는 음향학이나 양자역학과 같은 분야에서도 유사하게 사용된다.이 경우 가상의 전파 상수를 초래하는 파동 방정식에 대한 해법은 마찬가지로 "발진"이라고 불리며, 0이 아닌 장이 있어도 순 에너지가 전달되지 않는 본질적인 속성을 갖는다.

순간파 어플리케이션

광학 및 음향학에서, 매체를 여행하는 파동이 소위 임계각보다 큰 각도로 부딪치기 때문에 매체를 여행하는 파동이 그것의 경계에서 완전한 내부 반사를 겪을 때 발생된다.^[4]^[5]전파의 존재에 대한 물리적 설명은 전파장이 없는 경우처럼 전기장과 자기장(또는 음향파의 경우 압력 구배)을 경계에서 불연속할 수 없다는 것이다.양자역학에서 물리적 설명은 정확히 유사하다. 경계에서 정상적인 입자 운동을 나타내는 슈뢰딩거 파동 기능은 경계에서 불연속적일 수 없다.

전자파 방출파는 작은 입자에 광학적 방사선 압력을 가하여 실험용으로 가두거나 매우 낮은 온도로 냉각시키고 현미경을 위한 생물학적 세포나 단일 단백질과 DNA 분자와 같은 매우 작은 물체(총 내부 반사 형광현미경에서와 같이)를 밝히는 데 사용되어 왔다.pe). 광섬유의 반사파는 가스 센서에서 사용할 수 있으며, 감쇠된 총 반사율이라고 알려진 적외선 분광기법에서 반사파 수치가 된다.

전기 공학에서, 전파 안테나의 파장의 1/3 이내에서 근거리 지역에서 전파파가 발견된다.정상 작동 중에 안테나는 주변 근거리장 영역으로 전자기장을 방출하고, 전기장 에너지의 일부를 재흡수하며, 나머지는 전자파로 방사한다.

최근에는 그래핀 기반의 Bragg grating(일차원 광자 결정)이 제작되어 프리즘 커플링 기법을 이용해 주기구조의 표면 전자기파 흥분 능력을 입증하고 있다.^[6]

양자역학에서 슈뢰딩거 방정식의 반사파 해법은 파동-기계 터널링 현상을 일으킨다.

현미경 검사에서, 반사파에 포함된 정보를 포착하는 시스템은 초해상도 이미지를 만드는 데 사용될 수 있다.물질은 전파되는 전자파와 방출되는 전자파를 모두 방사한다.기존의 광학 시스템은 전파의 정보만 포착하기 때문에 회절 한도를 따른다.슈퍼렌즈 및 근거리 현장 스캐닝 광학 현미경과 같이 반사파에 포함된 정보를 캡처하는 시스템은 회절 한계를 극복할 수 있다. 그러나 이러한 시스템은 반사파를 정확하게 포착하는 시스템의 능력에 의해 제한된다.^[7]그들의 결의안에 대한 제한은 다음과 같다.

k\propto {\frac {1}{d}\ln {\frac {1}{\propto},

여기서 $k$ $k$ 은 $k$ 분해할 수 있는 최대파 벡터, $d$ $d$ 은 $d$ 물체와 센서 사이의 거리, $\delta$ ${\$ displaystyle $\style$ }은 센서의 $품질$ 을 측정하는 척도다 $\delta$ $.$

보다 일반적으로, 반사파의 실용적 적용은 (1) 원래 이동파가 반사되는 공간 영역 내에서 (예를 들어, 총 내부 반사 형광현미경에서와 같이) 어떤 다른 현상을 자극하기 위해 파동과 관련된 에너지를 사용하는 영역이나 (2) 그러한 영역으로 분류할 수 있다.전파파는 두 매체 사이의 공간 영역에서 이동파 해결책이 허용되지 않더라도 이동파가 허용되는 두 매체를 결합하여 매체 간 에너지 또는 입자 전달을 허용한다(사용 중인 파동 방정식에 대한 설명).그 예로는 소위 파동-기계 튜닝(tunnelling)이 있으며, 일반적으로 전파 커플링(evanescent wave coupling)으로 알려져 있다.

빛의 총 내부 반사량

내부반영합계

적색(반사파 생략)으로 인터페이스에서 (상단) 굴절 입사파 및 (하단) 전도파파를 나타낸다.

예를 들어, 미디어 간의 인터페이스가 x축에 놓여 있고, y를 따라 정규 분포를 따르고, z를 따라 양극화를 이루는 등, 2차원의 총체적 내부반사를 고려한다.총체적 내부반사로 이어지는 각도의 경우, 용액은 입사파와 반사파로 구성되며, 전송파가 전혀 없을 것으로 예상할 수 있지만, 맥스웰의 방정식에 따르는 그러한 해결책은 없다.유전체 매체의 맥스웰 방정식은 필드 E, H, D_y, B의_y 구성요소에 대해 연속성의 경계 조건을 부과한다.이 예에서 고려한 양극화의 경우, 입사 및 반사파의 이러한 구성요소는 파괴적으로 파괴되기 때문에 반사파가 입사 원과 동일한 진폭을 가질 경우 E와 B의_y 조건이 충족된다.그러나 H 부품은_x 구조적으로 중첩되므로 비파니싱 전송파가 없으면 해결책이 없다.그러나 전송되는 파동은 에너지를 경계로부터 멀리 운반하기 때문에 사인파가 될 수 없지만, 사건 및 반사파가 동일한 에너지를 가지기 때문에 에너지 보존에 위배된다.따라서 우리는 전송된 파동이 이동파가 아닌 맥스웰 방정식에 대한 비반사적 해결책이어야 하며, 유전체에서 그러한 해결책은 기하급수적으로 붕괴하는 것, 즉 소멸파라고 결론짓는다.

수학적으로, 반사파는 벡터의 성분 중 하나 이상이 상상의 값을 갖는 파동 벡터로 특징지어질 수 있다.벡터는 가상의 구성요소를 가지고 있기 때문에 실제 구성요소보다 적은 크기를 가질 수 있다.

$z=0$ $y$ {\ $displaystyle xy$ $}$ 평면의 $xy$ z $z=0$ = $z=0$ ${\displaystyle$ z $=0}$ 및 x $z=0$ $z$ ${\$ $displaystyle xz$ $}$ 평면의 $xz$ $y=0$ = $}$ 에 있는 두 매체의 인터페이스에 대해 $y=0$ 전송파의 파형 벡터는 형태를^[8] 가진다.

\mathbf{k_{t} \ =\k_{y}{\mathbf {y}{}}}{}+k_{x}{\mathbf {x}}}}}

with $k_{x}=k_{t}\sin \theta _{t}$ and $k_{y}=k_{t}\cos \theta _{t}$ , where $k_{t}$ is the magnitude of the wave vector of the transmitted wave (so the wavenumber), $\theta _{t}$ is굴절각및 ${\hat {\mathbf {x} }}$ ${\hat {\mathbf {x} }}$ ${\$ 과 ${\hat {\mathbf {x} }}$ ${\hat {\mathbf {y} }}$ ${\hat {\mathbf {y} }}$ ${\$ { $y}}}은($ 는 ${\hat {\mathbf {y} }}$ ) 각각 x ${\displaysty$ x}축 $x$ $y$ 과 y ${\displaysty y}$ 축 $y$ 방향을 따라가는 단위 벡터다.

By using the Snell's law $n_{i}\sin \theta _{i}=n_{t}\sin \theta _{t}$ where $n_{i}$ , $n_{t}$ , and $\theta _{i}$ are the refractive index of the medium where the incident wave and the reflected 파동이 존재하며, 전달 파동이 존재하는 매체의 굴절률 및 발생 각도는 각각,

k_{y}=k_{t}\cos \theta _{t}=\pm k_{t}\left(1-{\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}\right)^{1/2}

.

$n_{ti}={\frac {n_{t}}{n_{i}}}$ $n_{ti}={\frac {n_{t}}{n_{i}}}$ $n_{ti}={\frac {n_{t}}{n_{i}}}$ = $n_{ti}={\frac {n_{t}}{n_{i}}}$ $n_{ti}={\frac {n_{t}}{n_{i}}}$ $n_{ti}={\frac {n_{t}}{n_{i}}}$ ${\$

$\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ > $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ = $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ i {\ $displaystyle \sin$ \sin $\theta _{$ i}\ $sin \c}=n_$ {ti $\sin \theta _{i}>\sin \theta _{c}=n_{ti}$ 로 전체 내부 반영 조건의 일부가 충족되면, 그 다음,

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

=

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

±

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

(

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

i

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

i

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

2

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

-

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

)

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

/

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

2 = ±

k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha

{\displaystyle k_{y}=\pm ik_{t}\pm i_\frac {\sin ^{2}\{i}}}{i}^{n_{di}-1

}-1

\pm

i

\i

양극화가 발생 평면에 $z$ 인경우(z {\displaystyle $z}$ 방향을 $z$ 따라) 파동의 전기장(사건, 반사 또는 전송)은 다음과 같이 표현할 수 있다.

{\displaystyle \mathbf {r},t)=\mathrm {Re}\left\{E(\mathbf {r})\e^{i\omega t}\right\}\mathbf {\hat {z}}}}}}}}}}}}}}}}}}}}}""

여기서 $\scriptstyle \mathbf {\hat {z}}$ $\scriptstyle \mathbf {\hat {z}}$ ${\$ 은(는) $z$ ${\displaystyle$ z $}$ 축 $z$ 방향의 단위 벡터다 $\scriptstyle\mathbf{\hat{z}}$ .

By assuming plane waves as $E(\mathbf {r} )=E_{0}e^{-i\mathbf {k} \cdot \mathbf {r} }$ , and substituting the transmitted wave vector $\mathbf {k_{t}}$ into $\mathbf {k}$ , we find for the transmitted wave:

E(\mathbf {r} )=E_{o}e^{-i(-i\알파 y+\beta x)=}=E_{o}e^{-\알파 y-i\beta x}

where $\alpha =k_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}$ is the attenuation constant, and $\beta =k_{x}$ is the phase constant. $+i\alpha$ is ignored since it does 물리적으로 이치에 맞지 않는다(이 경우 방향 y를 따른 파동 증폭).

전등파 커플링

서로 다른 굴절 지수에 대한 파장 단위의 발생 각도에 대한 반사파의 1/e 침전 깊이의 그림.

특히 광학에서, 전파-파 커플링은 다른 방법으로는 전파에 해당하는 전파장으로 설명될 수 있는 두 파장의 물리적 중첩으로 인해 두 파장 사이의 결합을 말한다.^[9]

일반적으로 파동이 총 내부 반사를 겪는 밀집 매체의 표면에 매우 가까운(그래프 참조) FTIR(Frustrated Total Internal Reflection)이 주변의 또 다른 밀도 매체를 겹치는 대표적인 예가 있다.이것은 반사의 전체성을 교란시켜 어느 정도 힘을 제2의 매개로 분산시킨다.

두 광학적 도파관 사이의 결합은 한 요소에 의해 생성되는 발광장이 다른 광섬유의 파동을 유발하도록 섬유 코어를 서로 가깝게 배치하여 영향을 미칠 수 있다.이것은 광섬유 스플리터를 생산하고 섬유 태핑에 사용된다.무선 주파수(및 광학)에서는 그러한 장치를 방향 연결기라고 부른다.이 장치는 보통 마이크로파 전송과 변조의 경우 동력분할기라고 불린다.전자파-파 커플링은 전자기장 이론에서 근거리장 상호작용과 동의어다.소스 요소의 성질에 따라 관련되는 발광장은 이러한 요소들이 연결되는 원장(식별 위상, 자유 공간의 임피던스 비율)에서 (제안) 파동과 달리 주로 전기(용적) 또는 자기(유도)반사파 커플링은 각 매체 근처의 비방사성 장에서 발생하며, 이는 항상 물질과 관련된다. 즉, 부분적으로 반사되는 표면 내에서 유도 전류와 전하와 관련이 있다.양자역학에서 파동함수 상호작용은 입자의 관점에서 논의될 수 있으며 양자 터널링으로 설명될 수 있다.

적용들

반사파 커플링은 일반적으로 도파관 센서 또는 쿠플러로 광전자 및 나노전자 장치에 사용된다(예: 프리즘 커플러 참조).^[10]

예를 들어 유전체 마이크로스피어 공명기를 자극하기 위해 반사파 커플링을 사용한다.

근거리 전기장 상호작용과 마찬가지로 전자기 호환성에 관한 우려사항 중 하나이다.

섬유 태핑을 위한 손실 없는 광섬유의 결합.

비범한 광전송의 이론적 설명에 있어 반사파 커플링이 주요한 역할을 한다.^[11]

전파 커플링은 무선으로 장치에 전원을 공급하는데 사용된다.^[12]^[13]^[14]

토탈내반사 형광현미경은 토탈내반사에 의해 생성되는 반사파를 이용하여 표면에 가까운 불소포자를 흥분시킨다.이것은 생물 검체의 표면 특성을 연구해야 할 때 유용하다.^[15]

참고 항목

메모들

^ 또는 필드 E와 H를 페이저로 표현하여 복잡한 Poynting $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ S $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ = $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ ${\$ 은(는) 0의 실제 부분을 가진다 $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ .

참조

^ Takayama, O.; Bogdanov, A.A.; Lavrinenko, A.V. (2017). "Photonic surface waves on metamaterial interfaces". Journal of Physics: Condensed Matter. 29 (46): 463001. Bibcode:2017JPCM...29T3001T. doi:10.1088/1361-648X/aa8bdd. PMID 29053474.
^ IEEE Standard Dictionary of Electrical and Electronics Terms (IEEE STD 100-1992 ed.). New York: The Institute of Electrical and Electronics Engineers, Inc. 1992. p. 458. ISBN 978-1-55937-240-4.
^ Jackson, John David (1999), Classical Electrodynamics (3rd ed.), John-Wiley, ISBN 047130932X
^ Tineke Thio (2006). "A Bright Future for Subwavelength Light Sources". American Scientist. 94 (1): 40–47. doi:10.1511/2006.1.40.
^ Marston, Philip L.; Matula, T.J. (May 2002). "Scattering of acoustic evanescent waves". Journal of the Acoustical Society of America. 111 (5): 2378. Bibcode:2002ASAJ..111.2378M. doi:10.1121/1.4778056.
^ Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "Excitation of surface electromagnetic waves in a graphene-based Bragg grating". Scientific Reports. 2: 737. Bibcode:2012NatSR...2E.737S. doi:10.1038/srep00737. PMC 3471096. PMID 23071901.
^ Neice, A, "하파장 이미징의 방법과 한계", 이미지 및 전자 물리학의 진전, 2010년 7월 163권.
^ Hecht, Eugene (2017). Optics (5th Global ed.). Pearson. pp. 135–137. ISBN 978-1-292-09693-3.
^ Zeng, Shuwen; Yu, Xia; Law, Wing-Cheung; Zhang, Yating; Hu, Rui; Dinh, Xuan-Quyen; Ho, Ho-Pui; Yong, Ken-Tye (2013). "Size dependence of Au NP-enhanced surface plasmon resonance based on differential phase measurement". Sensors and Actuators B: Chemical. 176: 1128–1133. doi:10.1016/j.snb.2012.09.073.
^ Lova, Paola; Manfredi, Giovanni; Comoretto, Davide (2018). "Advances in Functional Solution Processed Planar 1D Photonic Crystals". Advanced Optical Materials. 6 (24): 1800730. doi:10.1002/adom.201800730. ISSN 2195-1071.
^ Fan, Zhiyuan; Zhan, Li; Hu, Xiao; Xia, Yuxing (2008). "Critical process of extraordinary optical transmission through periodic subwavelength hole array: Hole-assisted evanescent-field coupling". Optics Communications. 281 (21): 5467. Bibcode:2008OptCo.281.5467F. doi:10.1016/j.optcom.2008.07.077.
^ Karalis, Aristeidis; J.D. Joannopoulos; Marin Soljačić (February 2007). "Efficient wireless non-radiative mid-range energy transfer". Annals of Physics. 323 (1): 34. arXiv:physics/0611063. Bibcode:2008AnPhy.323...34K. doi:10.1016/j.aop.2007.04.017. S2CID 1887505.
^ Celeste Bieber, NewScientist.com, 2006년 11월 15일 "발광 커플링"은 무선으로 기기에 전원을 공급할 수 있다.
^ 무선 에너지가 소비자, 산업용 전자 장치에 동력을 공급할 수 있음 – MIT 보도 자료
^ Axelrod, D. (1 April 1981). "Cell-substrate contacts illuminated by total internal reflection fluorescence". The Journal of Cell Biology. 89 (1): 141–145. doi:10.1083/jcb.89.1.141. PMC 2111781. PMID 7014571.

외부 링크

[1] 또는 필드 E와 H를 페이저로 표현하여 복잡한 Poynting $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ S $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ = $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ ${\$ 은(는) 0의 실제 부분을 가진다 $\mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}$ .

[2] Takayama, O.; Bogdanov, A.A.; Lavrinenko, A.V. (2017). "Photonic surface waves on metamaterial interfaces". Journal of Physics: Condensed Matter. 29 (46): 463001. Bibcode:2017JPCM...29T3001T. doi:10.1088/1361-648X/aa8bdd. PMID 29053474.

[IEEEDict_1992-3] IEEE Standard Dictionary of Electrical and Electronics Terms (IEEE STD 100-1992 ed.). New York: The Institute of Electrical and Electronics Engineers, Inc. 1992. p. 458. ISBN 978-1-55937-240-4.

[Jackson_3rd-4] Jackson, John David (1999), Classical Electrodynamics (3rd ed.), John-Wiley, ISBN 047130932X

[Tineke-5] Tineke Thio (2006). "A Bright Future for Subwavelength Light Sources". American Scientist. 94 (1): 40–47. doi:10.1511/2006.1.40.

[Marstin-acoustic-6] Marston, Philip L.; Matula, T.J. (May 2002). "Scattering of acoustic evanescent waves". Journal of the Acoustical Society of America. 111 (5): 2378. Bibcode:2002ASAJ..111.2378M. doi:10.1121/1.4778056.

[7] Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "Excitation of surface electromagnetic waves in a graphene-based Bragg grating". Scientific Reports. 2: 737. Bibcode:2012NatSR...2E.737S. doi:10.1038/srep00737. PMC 3471096. PMID 23071901.

[8] Neice, A, "하파장 이미징의 방법과 한계", 이미지 및 전자 물리학의 진전, 2010년 7월 163권.

[9] Hecht, Eugene (2017). Optics (5th Global ed.). Pearson. pp. 135–137. ISBN 978-1-292-09693-3.

[10] Zeng, Shuwen; Yu, Xia; Law, Wing-Cheung; Zhang, Yating; Hu, Rui; Dinh, Xuan-Quyen; Ho, Ho-Pui; Yong, Ken-Tye (2013). "Size dependence of Au NP-enhanced surface plasmon resonance based on differential phase measurement". Sensors and Actuators B: Chemical. 176: 1128–1133. doi:10.1016/j.snb.2012.09.073.

[11] Lova, Paola; Manfredi, Giovanni; Comoretto, Davide (2018). "Advances in Functional Solution Processed Planar 1D Photonic Crystals". Advanced Optical Materials. 6 (24): 1800730. doi:10.1002/adom.201800730. ISSN 2195-1071.

[12] Fan, Zhiyuan; Zhan, Li; Hu, Xiao; Xia, Yuxing (2008). "Critical process of extraordinary optical transmission through periodic subwavelength hole array: Hole-assisted evanescent-field coupling". Optics Communications. 281 (21): 5467. Bibcode:2008OptCo.281.5467F. doi:10.1016/j.optcom.2008.07.077.

[13] Karalis, Aristeidis; J.D. Joannopoulos; Marin Soljačić (February 2007). "Efficient wireless non-radiative mid-range energy transfer". Annals of Physics. 323 (1): 34. arXiv:physics/0611063. Bibcode:2008AnPhy.323...34K. doi:10.1016/j.aop.2007.04.017. S2CID 1887505.

[14] Celeste Bieber, NewScientist.com, 2006년 11월 15일 "발광 커플링"은 무선으로 기기에 전원을 공급할 수 있다.

[15] 무선 에너지가 소비자, 산업용 전자 장치에 동력을 공급할 수 있음 – MIT 보도 자료

[16] Axelrod, D. (1 April 1981). "Cell-substrate contacts illuminated by total internal reflection fluorescence". The Journal of Cell Biology. 89 (1): 141–145. doi:10.1083/jcb.89.1.141. PMC 2111781. PMID 7014571.

[a]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Search