오류정정코드
Error correction code컴퓨팅, 전기통신, 정보이론 및 부호화 이론에서 오류 정정 코드, 때로는 오류 정정 코드(ECC)는 신뢰할 수 없거나 노이즈가 많은 통신 채널 [1][2]상의 데이터 오류를 제어하기 위해 사용됩니다.주된 생각은, 송신측이 ECC 형식의 용장 정보를 사용해 메시지를 부호화하는 것입니다.용장성에 의해, 수신자는 메시지내의 어느 장소에서도 발생할 가능성이 있는 한정된 수의 에러를 검출할 수 있습니다.또, 대부분의 경우, 재발송신 없이 이러한 에러를 수정할 수 있습니다.미국의 수학자 리처드 해밍은 1940년대에 이 분야를 개척했고 1950년에 최초의 오류 정정 코드인 [2]해밍(7,4)을 발명했다.
ECC는 발생한 오류를 단순히 검출하는 것이 아니라 수정할 수 있다는 점에서 오류 검출과 대조됩니다.ECC를 사용하는 시스템에서는 에러 발생 시 데이터 재전송을 요구하기 위해 리버스 채널을 필요로 하지 않는다는 장점이 있습니다.단점은 메시지에 추가되는 고정 오버헤드가 있기 때문에 더 높은 전송 채널 대역폭이 필요하다는 것입니다.따라서 ECC는 단방향 통신 링크와 같이 비용이 많이 들거나 재전송이 불가능한 상황이나 멀티캐스트 내의 여러 리시버로 전송되는 경우에 적용됩니다.천왕성 주위를 공전하는 위성의 경우 오류로 인한 재전송이 5시간 지연될 수 있기 때문에 긴 대기시간 연결도 도움이 됩니다.ECC 정보는 일반적으로 파손된 데이터를 복구하기 위해 대용량 스토리지 디바이스에 추가되며 모뎀에서 널리 사용되며 프라이머리 메모리가 ECC 메모리인 시스템에서 사용됩니다.
수신기의 ECC 처리는 디지털 비트스트림 또는 디지털 변조 반송파의 복조에 적용할 수 있다.후자의 경우, ECC는 수신기의 초기 아날로그-디지털 변환에 불가결한 부분입니다.Viterbi 디코더는 노이즈에 의해 손상된 아날로그 신호로부터 디지털 데이터를 복조하는 소프트 결정 알고리즘을 구현합니다.많은 ECC 인코더/디코더에서는 Bit Error Rate(BER; 비트 에러 레이트) 신호도 생성할 수 있습니다.이 신호는 아날로그 수신 전자 장치를 미세 조정하는 피드백으로 사용할 수 있습니다.
수정할 수 있는 오류 또는 누락된 비트의 최대 분율은 ECC 코드의 설계에 따라 결정되므로 조건에 따라 다른 오류 수정 코드가 적합합니다.일반적으로 코드가 강할수록 사용 가능한 대역폭을 사용하여 전송해야 하는 용장성이 높아집니다.이를 통해 수신된 유효 신호 대 잡음비가 개선되면서 유효 비트환율이 감소합니다.Claude Shannon의 노이즈 채널 코딩 정리를 사용하여 주어진 최대 허용 오차 확률에 대해 최대 도달 가능한 통신 대역폭을 계산할 수 있습니다.이것에 의해, 특정의 베이스 노이즈 레벨을 가지는 채널의 이론적인 최대 정보 전송 레이트에 대한 경계가 확립됩니다.그러나 증거는 건설적이지 않기 때문에 용량 달성 코드를 구축하는 방법에 대한 통찰력을 제공하지 않습니다.수년간의 연구 끝에 2016년 현재[3] 일부 첨단 ECC 시스템은 이론상 최대치에 매우 근접했습니다.
순방향 오류 수정
통신, 정보 이론 및 코딩 이론에서 순방향 오류 수정(FEC) 또는 채널[4][3] 코딩은 신뢰할 수 없거나 노이즈가 많은 통신 채널에서 데이터 전송 오류를 제어하기 위해 사용되는 기술입니다.주된 생각은, 송신자가, 대부분의 경우 ECC 를 사용해 메시지를 장황한 방법으로 부호화하는 것입니다.
용장성에 의해, 수신자는 메시지내의 어느 장소에서도 발생할 가능성이 있는 한정된 수의 에러를 검출할 수 있습니다.또, 재전송을 실시하지 않고, 이러한 에러를 수정할 수도 있습니다.FEC는 데이터 재전송을 요구하기 위해 리버스 채널을 필요로 하지 않고 고정적이고 높은 순방향 채널 대역폭을 희생하면서 수신기에 오류를 수정할 수 있는 기능을 제공합니다.따라서 FEC는 단방향 통신 링크 등 재전송이 비용이 많이 들거나 불가능한 상황이나 멀티캐스트 내의 여러 리시버로 전송되는 경우에 적용됩니다.FEC 정보는 일반적으로 파손된 데이터의 복구를 가능하게 하기 위해 대용량 스토리지(자기, 광학 및 솔리드 스테이트/플래시 기반) 디바이스에 추가됩니다.모뎀에서는 널리 사용됩니다.프라이머리 메모리가 ECC 메모리인 시스템이나 브로드캐스트 상황에서 리시버가 재전송을 요구하거나 재전송을 요구할 수 없는 경우 다음과 같이 사용됩니다.상당한 지연이 발생합니다.예를 들어, 천왕성 궤도를 도는 위성의 경우, 복호화 오류로 인해 재전송이 이루어지면 최소 5시간의 지연이 발생합니다.
리시버에서의 FEC 처리는 디지털 비트스트림 또는 디지털 변조 캐리어 복조에 적용할 수 있다.후자의 경우, FEC는 수신기의 초기 아날로그-디지털 변환에 불가결한 부분입니다.Viterbi 디코더는 노이즈에 의해 손상된 아날로그 신호로부터 디지털 데이터를 복조하는 소프트 결정 알고리즘을 구현합니다.많은 FEC 코더는 아날로그 수신 전자 장치를 미세 조정하는 피드백으로 사용할 수 있는 Bit Error Rate(BER; 비트 오류율) 신호를 생성할 수도 있습니다.
수정할 수 있는 오류 또는 누락된 비트의 최대 비율은 ECC 설계에 따라 결정되므로 조건에 따라 다른 전송 오류 수정 코드가 적합합니다.일반적으로 코드가 강할수록 사용 가능한 대역폭을 사용하여 전송해야 하는 용장성이 높아집니다.이를 통해 수신된 유효 신호 대 잡음비가 개선되면서 유효 비트환율이 감소합니다.Claude Shannon의 노이즈 채널 코딩 정리는 디코딩 오류 확률을 0으로 만드는 가장 효율적인 코드를 사용하면서 데이터 통신에 얼마나 많은 대역폭이 남아 있는지에 대한 질문에 답합니다.이것에 의해, 특정의 베이스 노이즈 레벨을 가지는 채널의 이론적인 최대 정보 전송 레이트에 대한 경계가 확립됩니다.그의 증거는 건설적이지 않기 때문에 용량 달성 코드를 구축하는 방법에 대한 통찰력을 제공하지 않습니다.그러나 수년간의 연구 끝에 폴라[3] 코드와 같은 일부 고급 FEC 시스템은 무한 길이 프레임이라는 가설 하에 섀넌 채널 용량을 달성합니다.
구조
ECC 는, 알고리즘을 사용해 송신된 정보에 용장성을 추가하는 것으로 실현됩니다.다중 비트는 많은 원본 정보 비트의 복잡한 함수일 수 있습니다.원래 정보는 문자 그대로 인코딩된 출력에 표시될 수도 있고 표시되지 않을 수도 있습니다.출력 중에 변경되지 않은 입력을 포함하는 코드는 체계적이지만 그렇지 않은 코드는 체계적이지 않습니다.
ECC의 간단한 예는 (3,1) 반복 코드라고 불리는 각 데이터 비트를 3회 전송하는 것입니다.노이즈가 많은 채널을 통해 수신기는 8가지 버전의 출력을 볼 수 있습니다(아래 표 참조).
| 삼중항 수신 | 로 해석되다 |
|---|---|
| 000 | 0(에러 없음) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (에러 없음) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
이를 통해 세 표본 중 하나의 오차를 "다수 투표" 또는 "민주 투표"로 수정할 수 있습니다.이 ECC의 수정 기능은 다음과 같습니다.
- 최대 1비트의 트리플렛 오류 또는
- 최대 2비트의 트리플렛 생략(표에는 기재되어 있지 않습니다).
구현이 간단하고 널리 사용되지만 이 트리플 모듈러 용장성은 상대적으로 비효율적인 ECC입니다.보다 나은 ECC 코드는 일반적으로 이전에 수신한 마지막 수십 비트 또는 마지막 수백 비트를 조사하여 현재 작은 소수의 비트(일반적으로 2 ~8비트 그룹)를 디코딩하는 방법을 결정합니다.
노이즈의 평균화를 통해 오류 감소
ECC는, 「노이즈 평균화」에 의해서 동작한다고 말할 수 있습니다.각 데이터 비트가 많은 송신 심볼에 영향을 미치기 때문에, 노이즈에 의한 일부 심볼의 파손은, 통상, 같은 유저 데이터에 의존하는 파손되지 않은 다른 수신 심볼로부터 원래의 유저 데이터를 추출할 수 있습니다.
- 이러한 "위험 풀링" 효과 때문에 ECC를 사용하는 디지털 통신 시스템은 일정한 최소 신호 대 잡음비를 훨씬 상회하는 경향이 있으며 그 이하가 아닙니다.
- 이 모든 것 또는 아무것도 하지 않는 경향, 즉 절벽 효과는 이론적인 Shannon 한계에 더 가깝게 접근하는 더 강력한 코드가 사용될수록 더욱 뚜렷해집니다.
- ECC 코드화된 데이터를 인터리빙하면 채널오류가 버스트 단위로 발생하는 경향이 있는 경우 송신된ECC 코드의 모든 속성 또는 전혀 속성을 줄일 수 있습니다.단, 이 방법에는 제한이 있습니다.협대역 데이터에 가장 적합합니다.
대부분의 통신 시스템은 예상되는 최악의 비트 에러 레이트를 허용하도록 설계된 고정 채널코드를 사용하여 비트 에러 레이트가 더 나빠지면 전혀 동작하지 않습니다.단, 특정 채널오류 조건에 적응하는 시스템도 있습니다.하이브리드 자동 반복 요구의 일부 인스턴스는 ECC가 에러 레이트를 처리할 수 있는 한 고정 ECC 방식을 사용하고, 에러 레이트가 너무 높아지면 ARQ로 전환합니다.어댑티브 변조 및 코딩은 다양한 ECC 레이트를 사용하여 패킷당 오류 수정 비트를 추가합니다.채널 내의 에러율이 높거나 필요하지 않을 때 에러율을 삭제합니다.
ECC의 종류
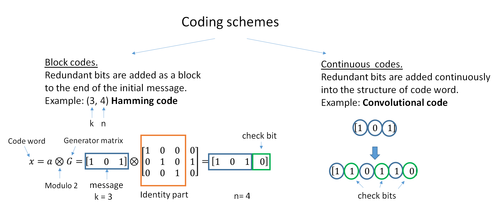
ECC 코드의 두 가지 주요 카테고리는 블록 코드와 컨볼루션 코드입니다.
- 블록 코드는 미리 정해진 크기의 비트 또는 기호로 구성된 고정 크기 블록(패킷)에서 작동합니다.실용적인 블록 코드는 일반적으로 다항식 시간으로 블록 길이로 하드 디코딩할 수 있습니다.
- 컨볼루션 코드는 임의의 길이의 비트 또는 심볼 스트림에서 작동합니다.대부분의 경우 Viterbi 알고리즘으로 소프트 디코딩되지만 다른 알고리즘이 사용되는 경우도 있습니다.비터비 디코딩은 컨볼루션 코드의 제약 길이 증가에 따라 점근적으로 최적의 디코딩 효율을 실현하지만, 그 복잡성은 기하급수적으로 증가합니다.종단되는 컨볼루션 코드는 입력 데이터의 블록을 인코딩한다는 점에서 '블록 코드'이기도 하지만, 컨볼루션 코드의 블록 사이즈는 일반적으로 임의인 반면 블록 코드는 그 대수적 특성에 의해 지시되는 고정 크기를 가진다.컨볼루션 코드의 종단 유형에는 "테일 비팅" 및 "비트 플러싱"이 있습니다.
블록 코드에는 많은 유형이 있습니다. 리드-솔로몬 코딩은 콤팩트 디스크, DVD 및 하드 디스크 드라이브에 널리 사용되기 때문에 주목할 만합니다.고전적인 블록 코드의 다른 예로는 골레이, BCH, 다차원 패리티 및 해밍 코드가 있습니다.
해밍 ECC는 NAND 플래시 메모리 [5]오류를 수정하기 위해 일반적으로 사용됩니다.이것에 의해, 싱글 비트의 에러 수정과 2 비트의 에러 검출이 가능하게 됩니다.해밍 코드는 보다 신뢰할 수 있는 싱글 레벨 셀(SLC) NAND에만 적합합니다.고밀도 멀티 레벨 셀(MLC) NAND는 BCH 또는 Reed-Solomon [6][7]등의 멀티 비트 보정 ECC를 사용할 수 있습니다.NOR 플래시는 일반적으로 오류 [6]수정을 사용하지 않습니다.
클래식 블록 코드는 보통 하드 결정 [8]알고리즘을 사용하여 디코딩됩니다.즉, 모든 입력 및 출력 신호에 대해 1비트에 대응하는지 0비트에 대응하는지 여부를 엄밀하게 판단합니다.대조적으로 컨볼루션 코드는 일반적으로 Viterbi, MAP 또는 BCJR 알고리즘과 같은 소프트 결정 알고리즘을 사용하여 디코딩되며, 아날로그 신호를 처리(분리)하여 하드 결정 디코딩보다 훨씬 높은 오류 수정 성능을 제공합니다.
거의 모든 고전 블록 코드는 유한 필드의 대수적 특성을 적용합니다.따라서 고전적인 블록 코드는 종종 대수적 코드라고 불립니다.
오류 검출 또는 오류 수정 기능을 지정하는 기존의 블록 코드와 달리 LDPC 코드와 같은 최신 블록 코드에는 이러한 보장이 없습니다.대신 최신 코드는 비트 오류율에 따라 평가됩니다.
대부분의 순방향 오류 수정 코드는 비트 플립만 수정하고 비트 삽입이나 비트 삭제는 수정하지 않습니다.이 설정에서는 Hamming 거리가 비트 오류율을 측정하는 적절한 방법입니다.일부 순방향 오류 수정 코드는 마커 코드 및 워터마크 코드와 같이 비트 삽입 및 비트 삭제를 수정하도록 설계되었습니다.Levenshtein 거리는 이러한 코드를 사용할 때 비트 오류율을 측정하는 더 적절한 방법입니다.[9]
코드 레이트와 신뢰성과 데이터 레이트의 트레이드오프
ECC의 기본 원칙은 디코더가 송신기에 의해 부호화된 진정한 메시지를 검출할 수 있도록 용장 비트를 추가하는 것입니다.소정의 ECC 시스템의 코드 레이트는, 소정의 통신 패키지내의 정보 비트수와 합계 비트수(즉, 정보+용장 비트)의 비율로 정의됩니다.따라서 코드 레이트는 실수입니다.코드 레이트가 0에 가까우면 다수의 용장 비트를 사용하여 양호한 성능을 달성하는 강력한 코드를 의미하며, 코드 레이트가 1에 가까우면 약한 코드를 의미합니다.
정보를 보호하는 용장 비트는 보호하려는 것과 동일한 통신 리소스를 사용하여 전송해야 합니다.이것에 의해, 신뢰성과 데이터 [10]레이트의 기본적인 트레이드 오프가 발생합니다.한 가지 극단적으로 강력한 코드(낮은 코드 레이트)는 유효 데이터 레이트를 감소시키는 비용으로 수신측 SNR(신호 대 잡음 비)의 중요한 증가를 유도할 수 있다.한편, 어떤 ECC도 사용하지 않는 경우(즉, 코드 레이트는 1과 동일)는 추가 보호 없이 비트를 남겨두는 비용으로 정보 전송 목적으로 전체 채널을 사용합니다.
한 가지 흥미로운 질문은 다음과 같습니다.정보 전송 측면에서 ECC는 디코딩 오류율이 무시할 수 있는 수준으로 얼마나 효율적일 수 있습니까?Claude Shannon은 두 번째 정리를 통해 이 질문에 답했습니다.즉, 채널 용량은 오류율이 0인 [11]ECC가 달성할 수 있는 최대 비트환율입니다.그의 증거는 실제 애플리케이션에 적합하지 않은 가우스 랜덤 코딩에 의존합니다.Shannon의 업적이 주는 상한선은 궁극의 성능 경계에 근접할 수 있는 ECC를 설계하는 데 오랜 여정을 불러일으켰습니다.오늘날 다양한 코드가 Shannon 한계에 거의 도달할 수 있습니다.그러나 ECC를 실현하는 용량은 일반적으로 구현이 매우 복잡합니다.
가장 일반적인 ECC는 퍼포먼스와 계산의 복잡성 사이에서 균형을 유지합니다.일반적으로 이들 파라미터는 시나리오에 따라 최적화할 수 있는 다양한 코드환율을 제공합니다.통상, 이 최적화는, 데이터 레이트에의 영향을 최소한으로 억제하면서, 디코딩 에러 확률을 낮게 하기 위해서 행해집니다.코드 레이트를 최적화하는 또 다른 기준은 통신의 에너지 [12]코스트에 맞추어 낮은 에러 레이트와 재전송 회수의 밸런스를 맞추는 것입니다.
성능 향상을 위한 ECC 코드 연결
고전적인 (대칭) 블록 코드와 컨볼루션 코드는 짧은 구속 길이의 비터비 디코딩된 컨볼루션 코드와 더 큰 심볼 크기와 블록 길이의 블록 코드(일반적으로 리드-솔로몬)가 컨볼루션 디코더에 의해 만들어진 오류를 "흡수"하는 연결 코딩 체계에서 자주 결합된다.이 에러 정정 코드 패밀리를 사용한 싱글 패스 디코딩에서는 에러율이 매우 낮을 수 있지만, 장거리 전송 조건(딥 스페이스 등)에서는 반복 디코딩을 권장합니다.
연결된 코드는 보이저 2호가 1986년 천왕성과의 조우에서 처음 이 기술을 사용한 이후 위성 및 심우주 통신에서 표준 관행이었다.갈릴레오 우주선은 안테나 고장으로 인한 매우 높은 오류율 조건을 보상하기 위해 반복적인 연결 코드를 사용했다.
저밀도 패리티 체크(LDPC)
Low-Density Parity-Check(LDPC; 저밀도 패리티 검사) 코드는 다수의 Single Parity Check(SPC; 단일 패리티 검사) 코드로 이루어진 고효율 선형 블록 코드 클래스입니다.블록 길이 측면에서 선형 시간 복잡성으로 반복된 소프트 결정 디코딩 방식을 사용하여 채널 용량(이론적인 최대값)에 매우 가까운 성능을 제공할 수 있습니다.실제 구현은 구성 SPC 코드를 병렬로 디코딩하는 데 크게 좌우됩니다.
LDPC 코드는 1960년 Robert G. Gallager에 의해 박사 논문에서 처음 도입되었지만, 인코더와 디코더를 구현하기 위한 계산 노력과 리드-솔로몬 코드의 도입으로 인해 1990년대까지 대부분 무시되었다.
LDPC 코드 지금 디지털 영상 방송-위성 2(DigitalVideoBroadcasting– 위성 – 2차 세대)는 와이 맥스(마이크로파 통신을 위해 IEEE802.16e표준) 같은 최근의 많은 고속 통신 표준에 사용된다, 고속 무선 LAN권력 놓여 네트워크를 구축 10GBase-T 이더넷(802.3an)과G.hn/G.9960(ITU-T표준(IEEE802.11n)[13]. 폰e라인 및 동축 케이블).기타 LDPC 코드는 3GPP MBMS 내의 무선 통신 표준에 대해 표준화되어 있습니다(분수 코드 참조).
터보 코드
터보 코딩은 2개 이상의 비교적 단순한 컨볼루션 코드와 인터리버를 결합하여 섀넌 한계 데시벨의 일부까지 수행할 수 있는 블록 코드를 생성하는 반복적인 소프트 디코딩 방식입니다.LDPC 코드보다 실용적 적용에 앞서 유사한 성능을 제공하게 되었습니다.
터보 코딩의 초기 상용 응용 프로그램 중 하나는 퀄컴이 개발하고 Verizon Wireless, Sprint 및 기타 통신사가 판매한 CDMA2000 1x(TIA IS-2000) 디지털 셀룰러 기술입니다.인터넷 액세스 전용 CDMA2000 1x, 1xEV-DO(TIA IS-856)의 진화에도 사용됩니다.1x와 마찬가지로 EV-DO는 퀄컴에 의해 개발되어 Verizon Wireless, Sprint 및 기타 통신사에 의해 판매되고 있습니다(1xEV-DO의 마케팅명은 Broadband Access, Sprint의 소비자 및 비즈니스 마케팅명은 각각 Power Vision 및 모바일 광대역입니다).
코드 로컬 디코딩 및 테스트
메시지의 단일 비트만 디코딩하거나 특정 신호가 코드워드인지 확인하고 신호 전체를 보지 않고 디코딩해야 하는 경우가 있습니다.이는 코드워드가 너무 커서 클래식하게 충분히 빨리 해독할 수 없고 현재로선 메시지의 몇 비트만 관심 있는 스트리밍 환경에서 의미가 있습니다.또한 그러한 코드는 계산 복잡도 이론에서 중요한 도구가 되었다. 예를 들어 확률적으로 확인할 수 있는 증명 설계를 위한 도구이다.
로컬 디코딩 가능한 코드는 코드워드가 일정한 위치에서 파손된 후에도 코드워드의 작은(예를 들어 일정한) 위치만 보고 메시지의 단일 비트를 확률적으로 복구할 수 있는 오류 수정 코드입니다.로컬 테스트 가능한 코드는 에러 수정 코드입니다.이 코드는 신호의 소수의 위치만 보고 신호가 코드워드에 가까운지 여부를 확률적으로 확인할 수 있습니다.
인터리빙
인터리빙은 순방향 오류 수정 코드의 성능을 개선하기 위해 디지털 통신 및 스토리지 시스템에서 자주 사용됩니다.많은 통신 채널은 메모리가 없는 것이 아닙니다.일반적으로 에러는 개별적으로 발생하는 것이 아니라 버스트에서 발생합니다.코드워드내의 에러수가 에러 정정 코드의 능력을 넘으면, 원래의 코드워드를 회복할 수 없게 됩니다.인터리빙을 사용하면 소스 기호를 여러 코드 워드에 걸쳐 섞음으로써 이 문제가 완화되고 오류의 분산이 보다 [14]균일해집니다.따라서 인터리빙은 버스트 오류 수정에 널리 사용됩니다.
터보 코드나 LDPC 코드와 같은 최신 반복 코드 분석은 일반적으로 [15]오류의 독립적인 분포를 가정합니다.따라서 LDPC 코드를 사용하는 시스템에서는 일반적으로 코드워드 [16]내의 심볼 전체에 추가 인터리빙이 사용됩니다.
터보 코드의 경우 인터리버는 일체형 컴포넌트이며 적절한 설계는 성능을 [14][17]향상시키기 위해 매우 중요합니다.반복 디코딩 알고리즘은 디코더를 나타내는 요인 그래프에 짧은 사이클이 없을 때 가장 잘 작동합니다. 인터리버는 짧은 사이클을 피하기 위해 선택됩니다.
인터리버 설계에는 다음이 포함됩니다.
- 직사각형(또는 균일한) 인터리버(위에서 설명한 건너뛰기 계수를 사용하는 방법과 유사함)
- 컨볼루션 인터리버
- 랜덤 인터리버(인터리버는 알려진 랜덤 순열)
- S-랜덤 인터리버(여기서 인터리버는 거리 S 내의 입력 [18]기호가 출력에서 S의 거리 내에 나타나지 않도록 제한되는 알려진 랜덤 순열입니다).
- 무경합 2차 순열 다항식(QPP)[19]입니다.사용 예는 3GPP Long Term Evolution 이동통신 [20]표준입니다.
멀티캐리어 통신 시스템에서는 예를 들어 주파수 선택 페이딩 또는 협대역 [21]간섭을 완화하기 위해 반송파 간의 인터리빙이 주파수 다양성을 제공하기 위해 사용될 수 있다.
예
인터리빙 없는 전송:
오류 없는 메시지: aaaabbbccddeeffg 전송과 버스트오류: aaaabbbccc__deeeffgg
여기서 같은 문자의 각 그룹은 4비트의 오류 수정 코드워드를 나타냅니다.코드워드 cccc는 1비트로 변경되어 수정이 가능하지만 코드워드 dddd는 3비트로 변경되어 디코딩이 전혀 불가능하거나 잘못 디코딩될 수 있습니다.
인터리빙 사용 시:
오류 없는 코드워드: aaaabbbccddeeffg Interleaved: abcdefgabcddefg 전송과 버스트오류: abcdefgabcd___bcdefg defg 인터리빙 후 수신된 코드워드: aa_abbbbbccddddddeff_g
"aaaa", "eee", "fffff" 및 "ggg"의 각 코드 워드는 1비트만 변경되므로 1비트 오류 수정 코드가 모든 것을 올바르게 디코딩합니다.
인터리빙 없는 전송:
원본 전송 문장:This IsAnExample Of인터리브 버스트 오류가 있는 수신된 문장:이것은______ple Of Interleaving 입니다.
"AnExample"이라는 용어는 대부분 이해하기 어렵고 수정하기 어렵습니다.
인터리빙 사용 시:
송신문:This IsAnExample Of인터리빙 중...에러 없는 전송: TIEPeaghsxlIrv.나는 Ani.snmOten.버스트 에러 TIEPFE____Irv.iAaenli.snmOten을 포함한 문장을 수신했습니다.인터리빙 해제 후 수신된 문장:T_isI_AnE_amp_eOfInterle_vin_...
단어를 완전히 잃어버리지 않고 최소한의 추측만으로 누락된 문자를 복구할 수 있습니다.
인터리빙의 단점
인터리빙 기술을 사용하면 총 지연이 증가합니다.이는 인터리브된 블록 전체를 수신해야 패킷을 [22]디코딩할 수 있기 때문입니다.또한 인터리버는 에러 구조를 숨깁니다.인터리버가 없으면 보다 고도의 디코딩 알고리즘이 에러 구조를 이용하여[citation needed] 인터리버와 조합된 보다 단순한 디코더보다 신뢰성 높은 통신을 실현할 수 있습니다.이러한 알고리즘의 예는 뉴럴[23] 네트워크 구조에 기초하고 있다.
에러 수정 코드용 소프트웨어
소프트웨어의 ECC(Error Correcting Code) 동작을 시뮬레이션하는 것은 ECC를 설계, 검증 및 개선하기 위한 일반적인 방법입니다.새로운 무선 5G 표준은 소프트웨어 ECC를 위한 새로운 범위의 애플리케이션, 즉 소프트웨어 정의 무선(SDR) 컨텍스트에서의 클라우드 무선 액세스 네트워크(C-RAN)를 제공합니다.소프트웨어 ECC를 통신에 직접 사용하는 것이 목적입니다.예를 들어 5G에서는 소프트웨어 ECC를 클라우드 내에 배치하고 이 컴퓨팅 리소스에 안테나를 연결할 수 있습니다.이렇게 하면 통신 네트워크의 유연성이 향상되어 최종적으로 시스템의 에너지 효율이 향상됩니다.
이 문맥에서는, 다음의 다양한 오픈 소스 소프트웨어가 이용 가능합니다(완전하지 않습니다).
- AFF3CT(A Fast Forward Error Correction Toolbox): C++(Turbo, LDPC, Polar code 등 지원되는 많은 코드)의 풀 통신 체인으로 매우 빠르고 채널 코딩에 특화되어 있습니다(시뮬레이션용 프로그램 또는 SDR의 라이브러리로 사용할 수 있습니다).
- IT++: 선형 대수, 수치 최적화, 신호 처리, 통신 및 통계용 클래스 및 함수의 C++ 라이브러리.
- OpenAir: 진화한 패킷코어 네트워크에 관한 3GPP 사양의 실장(C).
오류 수정 코드 목록
| 거리 | 코드 |
|---|---|
| 2 (단일 에러 검출) | 패리티 |
| 3 (단일 오류 수정) | 트리플 모듈러 용장성 |
| 3 (단일 오류 수정) | 해밍과 같은 완벽한 해밍(7,4) |
| 4 (SECDED) | 확장 해밍 |
| 5 (이중 오류 수정) | |
| 6 (이중 오류 정정/오류 검출) | 노드스트롬 로빈슨 코드 |
| 7 (3 에러 수정) | 완전 바이너리 골레이 코드 |
| 8 (TECFED) | 확장 바이너리 골레이 코드 |
- AN 코드
- BCH 코드. 코드 블록별로 임의의 수의 오류를 수정하도록 설계할 수 있습니다.
- 레이더, 원격측정, 울트라사운드, 와이파이, DSSS 휴대전화 네트워크, GPS 등에 사용되는 바커 코드.
- 버거 코드
- 고정 무게 코드
- 컨볼루션 코드
- 익스팬더 코드
- 그룹 코드
- 바이너리 골레이 코드가 실질적으로 관심 있는 골레이 코드
- Goppa 코드, McElece 암호 시스템에서 사용
- 아다마르 코드
- 헤겔바거 코드
- 해밍 코드
- 흰색 이외의 노이즈에 대한 라틴어 사각 기반 코드(전원선을 통한 광대역 등)
- 사전 코드
- 포인트 투 포인트링크가 아닌 네트워크상의 소거 수정 코드의 일종인 리니어 네트워크 코딩
- 긴 코드
- 저밀도 패리티 체크코드(Gallager 코드라고도 함)는 스파스 그래프 코드의 원형입니다.
- LT 코드: 거의 최적의 레이트리스 소거 수정 코드(분수 코드)
- m/n 코드
- 기하학[24] 및 군 이론에 사용되는 노드스트롬 로빈슨 코드
- 온라인 코드, 거의 최적의 레이트리스 삭제 수정 코드
- 폴라 코드(코드 이론)
- 랩터 코드, 거의 최적의 레이트리스 소거 수정 코드
- Reed-Solomon 오류 수정
- 리드-뮬러 코드
- 반복 누적 코드
- 트리플 모듈러 용장성 등의 반복 코드
- 척수 코드[25], 의사 랜덤 해시 함수에 기반한 무환율 비선형 코드
- 토네이도 코드, 최적에 가까운 소거 보정 코드 및 분수 코드의 전구체
- 터보 코드
- 월시-하다마르 코드
- CRC(Cyclic Redundancy Check)는 n(\display n의 최적의 제너레이터 다항식에 대해 - -1(\ 2 길이)의 메시지에 대한 1비트 오류를 수정할 수 있습니다. "Cyclic Redundancy Check 수학 #Bitfilters"를 참조하십시오.
참고 항목
참조
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). "Error Detecting and Error Correcting Codes". Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ a b c Maunder, Robert (2016). "Overview of Channel Coding".
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). "Forward Error-Correction Coding". Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work
{{cite journal}}:외부 링크quote= - ^ "낸드 플래시 메모리 장치의 해밍 코드" 2016년 8월 21일 웨이백 머신에 보관.EE 타임스 아시아분명히 "Micron Technical Note TN-29-08: NAND 플래시 메모리 장치의 해밍 코드"를 기반으로 합니다.2005. 둘 다 다음과 같이 말합니다. "Hamming 알고리즘은 많은 SLC NAND 플래시 기반 애플리케이션에서 오류 감지 및 수정을 위해 업계에서 인정받는 방법입니다."
- ^ a b "What Types of ECC Should Be Used on Flash Memory?" (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. ... Hamming based block codes are the most commonly used ECC for SLC.... both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). "The Inconvenient Truths of NAND Flash Memory" (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required ... for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). "A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions". International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). "Keyboards and covert channels". USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). "A mathematical theory of communication" (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). "Optimizing the code rate for achieving energy-efficient wireless communications". Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, 섹션 20.3.11.6 "802.11n-2009" Archived 2013년 2월 3일 IEEE, Wayback Machine, 2009년 10월 29일, 2011년 3월 21일에 액세스.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). "Practical Loss-Resilient Codes". Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ "Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)". En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). "The Development of Turbo and LDPC Codes for Deep-Space Applications". Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). "Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations". TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122...56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). "Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective". IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs........1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, 버전 8.8.0, 14페이지
- ^ "Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)". En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). "Explaining Interleaving". W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). "Deep Neural Network Probabilistic Decoder for Stabilizer Codes". Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR...711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), "An optimum nonlinear code", Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). "Rateless Spinal Codes". Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
추가 정보
- MacWilliams, 플로렌스 Jessiem, 슬론, 닐 제임스 알렉산더(2007년)[1977년].AT&T섀넌 LabsFlorham 공원, 뉴저지, 미국의 이론 Error-Correcting 코드에 쓰여진.North-Holland 수학 도서관이 있습니다.Vol16(12일 인상의 디지털 인쇄, 1판).암스테르담/런던/뉴욕/도쿄:North-Holland/엘제비어 BV.아이 에스비엔 978-0-444-85193-2.LCCN 76-41296.(xxii+762+6 페이지)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+4페이지)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- "싱글 레벨 셀 NAND 플래시 메모리 오류 수정 코드" 2007-02-16
- "낸드 플래시 메모리 오류 수정 코드" 2004-11-29
- James Hamilton, 2012-02-26에 의한 에러, 수정, 의존 시스템의 신뢰에 관한 관찰
- Sphere Packings, Ratites and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematic – 682 페이지
외부 링크
- Morelos-Zaragoza, Robert (2004). "The Correcting Codes (ECC) Page". Retrieved 5 March 2006.
- lpdec: LP 디코딩 및 관련 자료 라이브러리(Python)