버스트 오류 수정 코드

부호화 이론에서, 버스트 오류 수정 코드는 서로 독립적으로 비트에서 발생하기 보다는 연속적으로 여러 비트에서 발생하는 오류인 버스트 오류를 수정하는 방법을 채택한다.

많은 코드들이 무작위 오류를 수정하도록 설계되었다. 그러나 때때로 채널은 짧은 간격으로 국부적인 오류를 발생시킬 수 있다. 그러한 오류는 연속된 비트 수에서 발생하기 때문에 버스트(버스트 오류라고 함)에서 발생한다. 버스트 오류의 예는 저장 매체에서 광범위하게 찾아볼 수 있다. 이러한 오류는 디스크의 긁힘이나 무선 채널의 경우 번개와 같은 물리적 손상 때문일 수 있다. 그들은 독립적이지 않다; 그들은 공간적으로 집중되는 경향이 있다. 한 비트에 오류가 있으면 인접한 비트도 손상될 수 있다. 무작위 오류를 수정하는 데 사용되는 방법은 버스트 오류를 수정하는 데 비효율적이다.

정의들

버스트 길이 $\ell {\displaystyle }$ ${\displaystyle \ell}$

코드 $워드{\displaystyle }$ C ${\displaystyle C$}이$$(가) $전송$되고 Y${\displaystyle }$=${\displaystyle C}$ + ${\displaystyle E.}$ ${\displaystyle$Y=$C+E.}$로 수신된다고 가정하십시오.$$ 그런 다음 $E{\displaystyle }$ ${\displaystyle E}$의 0이 아닌 구성 $요소$가 {$${\displaystyle \ell$}$ 연속$$ 구성 요소로 제한되는$$ 경우$$ 오류 $벡터{\displaystyle }$ E${\$displaystyle \$ell$$}$을(를) 길이의 버스트 $\ell {\displaystyle }$ ${\$$displaystystyle$ \ell}이라고 한다. 예를 들어 $E{\displaystyle }$= (${\displaystyle 0}$ ${\displaystyle 1000011\mathrm{}}$ 0${\displaystyle }$) ${\displaystyle E=(0{\textbf{1000011}}}}}은($는) 길이의 버스트${\displaystyle \mathrm{\ell }}$ = 7. ${\displaystyle \ell$=7)이다$.$$}$

이 정의는 버스트 오류가 무엇인지 설명하기에 충분하지만, 버스트 오류 수정을 위해 개발된 도구의 대부분은 주기 코드에 의존한다. 이것은 우리의 다음 정의에 동기를 부여한다.

순환 버스트 길이 $\ell {\displaystyle }$ ${\displaystyle \ell}$

$오류{\displaystyle }$ 벡터 E ${\displaystyle E}$은(는) 0이 아닌 구성 요소가 $\ell {\displaystyle }$ ${\displaystyle \ell }$ 순환$$ 연속 구성 요소로 제한되는 경우$$ 길이 $\ell {\displaystyle }$ ${\displaystyle \ell$}의 순환 버스트 오류라고 불린다$$. 예를 들어 이전에 고려된 오류 벡터 $E{\displaystyle }$= (${\displaystyle 010000110}$ )${\displaystyle$ E$=(010000110$은 위치 $6{\displaystyle \mathrm{}}$ ${\displaystyle 6}$에서 시작하여 위치 $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$에서 끝나는 오류를 고려하므로 길이 ${\displaystyle \mathrm{\ell }}$= 5 ${\displaystyle$=$5}$의 $순환{\displaystyle \mathrm{}}$ 버스트입니다$.$$e 0}$ - 기반$$, 즉 첫 번째 요소가 위치 $0{\displaystyle \mathrm{}}$ ${\displaystyle 0}$에 있음$.$

이 글의 나머지 부분에 대해서는 달리 언급하지 않는 한, 우리는 버스트라는 용어를 사용하여 주기적 버스트를 지칭할 것이다.

버스트 설명

버스트 오차의 길이뿐만 아니라 패턴과 위치를 포함하는 버스트 오차의 작은 정의를 갖는 것이 종종 유용하다. 버스트 설명을 튜플$({\displaystyle P}$, L${\displaystyle }$) ${\displaystyle(P,L)}($여기서$$ $P{\displaystyle }$ ${\displaystyle$ P$}$은(는) 오류 패턴의 첫 번째 0이 아닌 항목으로 시작하여 마지막 0이 아닌 기호로 끝나는 기호 문자열)으로 정의하고$$L {\$displaysty$ L$}$은 코드 워드에서 위치(w)로$$ 정의한다.폭발물을 찾을 수 있을 것이다.^[1]

For example, the burst description of the error pattern ${\displaystyle E=(010000110)}$ is ${\displaystyle D=(1000011,1)}$. Notice that such description is not unique, because ${\displaystyle D'=(11001,6)}$ describes the same burst error. 일반적으로 $E{\displaystyle }$ ${\displaystyle E}$에서 0이 아닌 구성 요소 수가 w ${\displaystyle w$인 경우 $E{\displaystyle }$ ${\displaystyle E}$의 서로 다른 0이 아닌 $항목$에서 시작하는 $각각{\displaystyle }$ w$${\$displaystyle w}$개의$$ 버스트 설명이 있음$$$.$ 버스트 설명의 모호성으로 인해 발생하는 문제를 해결하기 위해그러나 하기 정리하기 전에 우리는 먼저 정의가 필요하다.

정의. 주어진 오류 $패턴{\displaystyle }$ y${\displaystyle }$, ${\displaystyle$ y$,}$에 있는 기호 $수$는 l ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{n}}$ g ${\displaystyle \mathrm{t}}$ ${\displaystyle \mathrm{h}}$( y${\displaystyle }$)${\displaystyle }$. ${\displaystyle \mathrm$ {$length} (y$)로 표시된다$.$$}$

정리(버스트 설명의 고유성). Suppose ${\displaystyle E}$ is an error vector of length ${\displaystyle n}$ with two burst descriptions ${\displaystyle (P_{1},L_{1})}$ and ${\displaystyle (P_{2},L_{2})}$. If ${\displaystyle \mathrm {length$${}(P_{1}+\mathrm {length}(P_{2})\leqslant n+1,}$ 그러면 두 설명은$$ 동일하며, 즉 해당 구성 요소가 동일하다.^[2]

증명. $w{\displaystyle }$ ${\displaystyle w}$을(를) $E{\displaystyle }$ ${\displaystyle E}$의 해밍 가중치(또는 0이 아닌 항목 수)로$$ 설정$.$ 그러면 $E{\displaystyle }$ ${\displaystyle E}$에 정확히$$ $w{\displaystyle }$ ${\displaystyle w}$ 오류$$ 설명이 있음. $w{\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle 1}$,${\displaystyle w=0,1,}$의 경우 증명할 것이 없다$$. 따라서 $w{\displaystyle }$ ${\displaystyle ⩾}$ ${\displaystyle 2}$ ${\displaystyle w\geqslant 2}$과(와) 설명이 동일하지 않다고 가정한다. $E{\displaystyle }$ ${\displaystyle E}$의 각 비제로 엔트리가 패턴에 나타나므로$$ $패턴$에 포함되지$$ 않은 E ${\displaystyle E}$의 구성 요소는 마지막 비제로 엔트리를 시작한 직후에 0의 순환 런을 형성하고 패턴의 첫 번째 비제로 엔트리를 바로 앞에 계속한다. 이 런에 해당하는 지수 집합을 영점 런이라고 부른다. 우리는 즉시 각 버스트 설명에 관련된 제로 런이 있고 각 제로 런이 분리된다는 것을 관찰한다. $w{\displaystyle }$ ${\displaystyle w}$ 0$$ 런이 있고 각 런이 분리되므로 모든 0 런에 총 $n{\displaystyle }$- ${\displaystyle w}$ ${\displaystyle n-w}$개의$$ 개별 요소가 있다. 반면에 우리는 다음을 가지고 있다.

${\displaystyle {\begin}n-w={\text{n-w={\n-\mathrm {length}(P_{1})+(n-\mathrm {length}(P_{2})의 0 수\\&=2n-\left(\mathrm {length})(P_{1}+\mathrm {length}(P_{2})\right)\&\geqslant 2n-(n+1)&\mathrm {length}(P_{1})+\mathrm {length}(P_{2})\leqslant n+1\&=n-1\ed}}}}}$

이는 $w{\displaystyle }$ ${\displaystyle ⩾}$ 2${\displaystyle w\geqslant 2.}$과 모순되므로 버스트 오류 설명은 동일하다.

위의 정리 중 중요한 것은 길이 ${\displaystyle \frac{1}{}}$ $2{\displaystyle \frac{\mathrm{}}{}}$( ${\displaystyle n}$+ ${\displaystyle 1}$)$$. {\$displaystyle {\tfrac{1}{2}}(n+1$)의 버스트에 대해 두 개의 뚜렷한 버스트 설명을 가질 수 없다는 것이다$.$$}$

버스트 오류 수정을 위한 주기 코드

순환 코드는 다음과 같이 정의된다: $q{\displaystyle }$ ${\$$$$\mathb {F} _{q}$의 원소로$$q ${\$displaystyle $\mathb$ {F} _{q}. 이제 단어의 개별 기호가 다항식 계수에 해당하는 $F$${\displaystyle {}_{}}$ , {\$displaystystymathb {F}$_${q}$에 대한 다항목으로 생각할 수 있다.l. 순환 코드를 정의하기 위해, 우리는 발전기 다항식이라고 불리는 고정 다항식을 선택한다. 이 순환 코드의 암호어는 모두 이 발전기 다항식으로 구분할 수 없는 다항식이다.

Codewords are polynomials of degree ${\displaystyle \leqslant n-1}$. Suppose that the generator polynomial ${\displaystyle g(x)}$ has degree ${\displaystyle r}$. Polynomials of degree ${\displaystyle \leqslant n-1}$ that are divisible by ${\displaystyle g(x)}$ result from multiplying $$${\displaystyle g}$( ${\displaystyle x}$) ${\displaystyle g(x)}$ 도 $⩽{\displaystyle }$ ${\displaystyle n}$- ${\displaystyle 1}$-${\displaystyle {}^{}}$${\displaystyle \mathrm{r}}$ ${\displaystyle \leqslant n-1-r}$의 다항식$.$ 이러한$$ ${\displaystyle {다항식}^{}}$ ${\displaystyle q^{}}$- r {\$displaystyle q$^{n-r$}$이 있다. 각각 암호어에 해당된다. 따라서$$ $주기{\displaystyle \mathrm{코드}}$의 경우${\displaystyle k}$ =$$n - r {\$displaystyle$ k=$n-r}$

Cyclic codes can detect all bursts of length up to ${\displaystyle \ell =n-k=r}$. We will see later that the burst error detection ability of any ${\displaystyle (n,k)}$ code is bounded from above by ${\displaystyle \ell \leqslant n-k}$. Cyclic codes are considered optimal for burst error detection 상한을 충족하기 때문에:

정리(순환 버스트 보정 능력) 발전기 다항식 $r{\displaystyle }$ ${\displaystyle r}$을(를) 사용하는 모든 주기 코드는 길이의 모든 버스트를 감지할 수 있다$$.${\displaystyle }⩽{\displaystyle }$ ${\displaystyle r}$ . ${\displaystyle \leqslant r.}$

Proof. We need to prove that if you add a burst of length ${\displaystyle \leqslant r}$ to a codeword (i.e. to a polynomial that is divisible by ${\displaystyle g(x)}$), then the result is not going to be a codeword (i.e. the corresponding polynomial is not divisible by ${\displaystyle g(x)}$). 길이 $⩽{\displaystyle }$ ${\displaystyle r}$${\displaystyle \leqslant r}$의 버스트가 $g{\displaystyle }$( x${\displaystyle }$) ${\displaystyle g($${\displaystyle x}$$)}$에 의해 분할되지$$ 않음을 보여 주는 것으로 충분하다$.$ 이러한 버스트는 $x{\displaystyle {}^{}}$ i ${\displaystyle {}^{}}$() ${\displaysty$ x$^{ib(x$ 여기서 $deg$ ){\$displaysty)($$x)>.$$}$ ${\displaystyle \mathrm{따라서<img\; alt="\{\backslash displaystyle\; \backslash deg(b(x))<r.\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/12bb3418b3c30539ec28ffce25220433cedcbd72"\; style="vertical-align:\; -0.838ex;\; width:14.227ex;\; height:2.843ex;"\; papago-attr-id="177">}}$ b${\displaystyle }$( x${\displaystyle }$) ${\displaystyle b(x)}$은(는) $g{\displaystyle }$( x${\displaystyle }$) ${\displaystyle$ $g$$(x)}($$후자$가 도 $$r ${\displaystyle$ $r$$})$을$($를) 가지므로 $g{\displaystyle }$($x)$는) $x{\displaystyle }$${\displaystystyle$ x$}(또는$ $모든{\displaystyle \mathrm{}}$ 코드)$$$$로 구분되지 않는다. 따라서 $x{\displaystyle {}^{}}$ ${\displaystyle i^{}}$ ${\$ x$^{i}$는 $g{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle g(x)}$로도 분할되지 않는다$$.

위의 증거는 순환 코드의 버스트 오류 감지/교정을 위한 간단한 알고리즘을 제안한다: 전송된 단어(${\displaystyle 즉}$, 도 $⩽{\displaystyle }$ ${\displaystyle \mathrm{n}}$- 1 ${\displaystyle \leqslant n-1})$가 주어진 경우,$$ $g{\displaystyle }$(${\displaystyle x}$ ${\displaystyle )}$ ${\displaysty g(x)}$로 나눌 때 이 단어의 나머지를 계산한다$.$ 나머지가 0인 경우(즉, 단어가 분할된 경우).${\displaystyle g}$( ${\displaystyle x}$) ${\displaystyle g(x)})$를 선택한 다음 유효한 코드 워드가 된다. 그렇지 않으면 오류를 보고하십시오. 이 오류를 수정하려면 전송된 단어에서 이 나머지를 빼십시오. 뺄셈 결과는 $g{\displaystyle }$( x${\displaystyle }$) ${\displaystyle g(x)}($즉, 유효한 코드 워드가 될 것이다)$$로 나눌 수 있다.

버스트에 대한 오류 감지 상한( by ${\displaystyle ⩽}$ ${\displaystyle n}$- k${\displaystyle }$= ${\displaystyle r}$ ${\displaystyle \ell \leqslant n-k=r})$에 의해, 우리는 순환 코드가 > {\$displaystyle \ell$ >$r}$의 모든 버스트를 감지할 수 없다는 것을 알고 있다 그러나 순환 코드는 실제로길이 > {\d. The reason is that detection fails only when the burst is divisible by ${\displaystyle g(x)}$. Over binary alphabets, there exist ${\displaystyle 2^{\ell -2}}$ bursts of length ${\displaystyle \ell }$. Out of those, only ${\displaystyle 2^{\ell -2-r}}$ are divisible by ${\d$$isplaystyle g(x$ 따라서 검출 실패 확률이 매우 작다(${\displaystyle {\mathrm{}}^{}}$- r ${\$ 2$^{-r$ 모든 버스트 길이의 균일한 분포를 $가정$한다. ( ${\displaystyle \ell }$.

이제 우리는 버스트를 다른 코스메트로 분류함으로써 효율적인 버스트 오류 수정 코드를 설계하는 데 도움이 될 순환 코드에 대한 근본적인 정리를 고려한다.

정리(Distinct Cosets). 선형 코드 $C{\displaystyle }$ ${\displaystyle C}$은(는) 길이의 모든 버스트 오류가 ${\displaystyle$ $\backslash {\displaystyle }$$ell}$의 고유 코세트에 있는$$ 경우 $\ell {\displaystyle }$ ${\displaystyle$ \explaystyle $\leqslant \ell}$ -burst-error-correction$$ 코드 입니다$.$

Proof. Let ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}$ be distinct burst errors of length ${\displaystyle \leqslant \ell }$ which lie in same coset of code ${\displaystyle C}$. Then ${\displaystyle \mathbf {c} =\mathbf {e} _{1}-\mathbf {e} _{2}}$ is a codeword. Hence, if we receive ${\displaystyle \mathbf {e} _{1},}$ we can decode it either to ${\displaystyle \mathbf {0} }$ or ${\displaystyle \mathbf {c} }$. In contrast, if all the burst errors ${\displaystyle \mathbf {e} _{1}}$ and ${\displaystyle \mathbf {e} _{2}}$ do not lie in same 코제트, 그리고 나서 각각의 버스트 오차는 그것의 증후군에 의해 결정된다. 그 오류는 그 증후군을 통해 고쳐질 수 있다. 따라서 길이 $⩽{\displaystyle }$의 모든 버스트 오류가 $C{\displaystyle }$ ${\displaystyle C}$의 구별되는 코세트에 존재하는$$ 경우에만 $선형{\displaystyle }$ 코드 $C{\displaystyle }$ ${\$$displaystyle \ell} -burst-error-correction$ 코드 입니다$.$

정리(버스트 오류 코드워드 분류). $C{\displaystyle }$ ${\displaystyle C}$을(를) 선형 $\ell {\displaystyle }$ ${\displaystyle \ell}$ -burst-error-correction$$ 코드로 설정하십시오$$. 그러면$$ 길이 $⩽{\displaystyle }$ ${\displaystyle 2}$ ${\displaystyle \ell }$ ${\displaystyle \leqslant 2\ell }$의 nonzero burst가 코드 워드가 될 수 없다.

Proof. Let ${\displaystyle c}$ be a codeword with a burst of length ${\displaystyle \leqslant 2\ell }$. Thus it has the pattern ${\displaystyle (0,1,u,v,1,0)}$, where ${\displaystyle u}$ and ${\displaystyle v}$ are words of length ${\displaystyle \leqslant \ell -1.}$ Hence, the words ${\displaystyle w=(0,1,u,0,0,0)}$ and ${\displaystyle c-w=(0,0,0,v,1,0)}$ are two bursts of length ${\displaystyle \leqslant \ell }$. For binary linear codes, they belong to the same coset. 이것은 구별되는 코제트 정리와 모순되므로 길이${\displaystyle }$length ${\displaystyle 2}$ $[\displaystyle \leqslant 2\ell }$의 논제로 버스트는 암호어가 될 수 없다$$.

버스트 오류 수정 한계

버스트 오류 감지 및 수정의 상한

상한선이란 결코 넘어설 수 없는 오류 감지 능력에 대한 한계를 의미한다. 길이 $⩽{\displaystyle }$의 모든 버스트 오류를 감지할 수 있는 $({\displaystyle n}$, k${\displaystyle }$) ${\$$displaystyle$ $(n,k)}$코드를$$ 설계하고 싶다고 가정해 봅시다$.$ {\$displaystyle$ $\leqslant \ell .}$ 자연스런$$ 질문: $n{\displaystyle }$ ${\$displaystyle $n}$과 $k{\displaystyle }$ ${\displaystystyle k$ 우리가 결코 달성할 수 없는 $최대$$\ell$},d? 다시 말해, 임의의 $({\displaystyle n}$ ${\displaystyle ,}$ k${\displaystyle }$) ${\displaystyle (n,k)$ 코드를$$ 사용하여 탐지할 수 있는 버스트 길이$$ $\ell {\displaystyle }$ ${\displaystyle \ell }$의 상한은? 다음의 정리는 이 질문에 대한 해답을 제공한다.

정리(버스트 오류 감지 능력). (n${\displaystyle }$,${\displaystyle k}$ ) ${\displaystyle \{\backslash }$displaystyle ($n,k$)}$$코드의$$ 버스트 오류 감지 능력은 ability${\displaystyle }\ell {\displaystyle }$ ${\displaystyle n}$- ${\displaystyle k}$. ${\displaystyle \ell \leqslant n-k이다.$$}$

Proof. First we observe that a code can detect all bursts of length ${\displaystyle \leqslant \ell }$ if and only if no two codewords differ by a burst of length ${\displaystyle \leqslant \ell }$. Suppose that we have two code words ${\displaystyle \mathbf {c} _{1}}$ and ${\displaystyle \mathbf {c}$$_{2}}:$ 길이${\displaystyle }$${\$의 버스트 b$${\$displaystyle \leqslant \ell$에 따라 다른$$. ${\displaystyle {\mathrm{}}_{}}$ $1{\displaystyle {\mathbf{}}_{}}$ ${\${$c}$$_{$$1$}을 수신할 때 전송된 단어가 $실제로{\displaystyle {\mathbf{}}_{}}$ c ${\displaystyle {}_{}}$인지, 전송 오류가 없는지$$$,$ 또는 {$c}$을 알 수 없다.${\displaystyle {\mathbf{c}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$ 전송$$ 중에 발생한 버스트 오류 $b{\displaystyle \mathbf{}}$ ${\$ 자, 두 개의 코드 단어마다 길이가 $burst{\displaystyle }$$.$ $.{\displaystyle \ell .}$의 $버스트{\displaystyle \mathbf{}}$ b$${\$displaystyle \mathbf {c}$ $\_{\displaystyle }$${1$}에 의해 전송된$$ ${\displaystyle {\mathrm{}}_{}}$ c $1{\displaystyle {\mathbf{}}_{}}$ ${\$$displaystyle \$$mathbf${$b}}{$1}{1}가 맞더라도 다른$$ 유효한 코드wor로 변경되지는 않을 것이다$.$d. 그것을 받으면 우리는 $이것$이 $b{\displaystyle {\mathbf{}}_{}}$${\displaystyle .}$ ${\displaystyle \mathbf$$${$c}$$_{1$}라는$$ 것을 알 수 있다$.$ 위의 관찰에 따르면$$, 우리는 두 개의 암호어가 첫 $번째{\displaystyle }$ n -${\displaystyle \ell }$ ${\displaystyle n-\ell}$ 기호를$$ 공유할 수 없다는 것을 안다. The reason is that even if they differ in all the other ${\displaystyle \ell }$ symbols, they are still going to be different by a burst of length ${\displaystyle \ell .}$ Therefore, the number of codewords ${\displaystyle q^{k}}$ satisfies ${\displaystyle q^{k}\leqslant q^{n-\ell }.}$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle q_{}}$ ${\$를 양쪽에$$ 적용하고 재배열하면 $\ell {\displaystyle }$ ${\displaystyle ⩽}$ ${\displaystyle n}$- ${\displaystyle k}$ ${\displaystyle \ell \leqslant n-k}$을(를) 확인할 수 있다$.$

이제 동일한 질문을 반복하지만 오류 수정에 $대해서$는 n ${\displaystyle n$${\displaystyle \}}$ 및$$ $k{\displaystyle }$ ${\displaystyle k}$을$($를$)$ 사용할 때 수정할${\displaystyle }$수 있는 버스트 길이$$ $\ell {\displaystyle }$ ${\$$displaystyle \ell }$의 상한은? 다음 정리는 이 질문에 대한 예비적인 답을 제공한다.

정리(버스트 오류 보정 능력). 임의의${\displaystyle }$(${\displaystyle n}$, ${\displaystyle k}$) ${\displaystyle (n,$k$$$)}$ 코드의 버스트 오류 수정 능력은 $\ell {\displaystyle }$ ${\displaystyle ⩽}$ ${\displaystyle n}$- ${\displaystyle k}$- ${\displaystyle {\log }_{}}$ ${\displaystyle \mathrm{q}}$ ${\displaystyle {}_{}}$ ${\displaystyle (n}$- ${\displaystyle \ell }$)${\displaystyle }$+ 2 ${\displaystyle \ell \leqslant n-k-\log _{q}(n-\ell )+2}$을 만족한다.

증명. 먼저 두 개의 코드 단어가 두 개의 ${\displaystyle \mathrm{길이}}$의 버스트 합계로 차이가 나지 않는 경우에만$$ 코드에서 길이${\displaystyle \leqslant \ell }$의 모든 버스트를 수정할 수 있다는 것을 관찰한다${\displaystyle .}${\$displaystyle$ 두 개의 코드 ${\displaystyle {\mathrm{}}_{}}$ c 1 ${\\\$} ${\displaystyle {}_{}}$ 2 \$mathb$}{1}{$ma$\$styption\$stytype}$thbf {c} _{2$}}개씩 버스트 $b{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$및$$ $b{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$개$$ 길이$$${\displaystyle \ell }$ ${\displaysty \leqslant \ell}$에 따라 다르다$$. Upon receiving ${\displaystyle \mathbf {c} _{1}}$ hit by a burst ${\displaystyle \mathbf {b} _{1}}$, we could interpret that as if it was ${\displaystyle \mathbf {c} _{2}}$ hit by a burst ${\displaystyle -\mathbf {b} _{2}}$. We can not tell whether the transmitted word is ${\displaystyle {\mathbf{c}}_{}}$${\displaystyle \mathbf {c} _{1}}$ or ${\displaystyle \mathbf {c} _{2}}$. Now, suppose that every two codewords differ by more than two bursts of length ${\displaystyle \ell }$. Even if the transmitted codeword ${\displaystyle \mathbf {c} _{1}}$ is hit by a burst of length ${\displaystyle \ell }$$$그것은 또 다른 폭발에 의해 강타당한 또 다른 암호어처럼 보이지 않을 것이다. For each codeword ${\displaystyle \mathbf {c} ,}$ let ${\displaystyle B(\mathbf {c} )}$ denote the set of all words that differ from ${\displaystyle \mathbf {c} }$ by a burst of length ${\displaystyle \leqslant \ell .}$ Notice that ${\displaystyle B(\mathbf {c} )}$ includes ${\displaystyle \mathbf{c}}$${\displaystyle \mathbf {c}$ 그 자체$$. By the above observation, we know that for two different codewords ${\displaystyle \mathbf {c} _{i}}$ and ${\displaystyle \mathbf {c} _{j},B(\mathbf {c} _{i})}$ and ${\displaystyle B(\mathbf {c} _{j})}$ are disjoint. $q{\displaystyle {}^{}}$ ${\displaystyle k^{}}$ ${\$ 코드 워드가$$ 있다. Therefore, we can say that ${\displaystyle q^{k} B(\mathbf {c} ) \leqslant q^{n}}$. Moreover, we have ${\displaystyle (n-\ell )q^{\ell -2}\leqslant B(\mathbf {c} ) }$. By plugging the latter inequality into the former, then taking the base ${\displays$$tyle q}$ logarithm과$$ 재배열, 우리는 위의 정리를 얻는다.

더 강한 결과는 리거 바운드에 의해 주어진다.

정리(리거 바운드). ▼ ${\displaystyle \ell}$이$({\displaystyle }$가) (${\displaystyle n}$ ${\displaystyle ,}$ k${\displaystyle }$) ${\displaystyle(n,k)}$ 선형$$ 블록 코드의 기능을 수정하는 버스트 오류인 경우, 2 ${\displaystyle \ell }$ ${\displaystyle ⩽}$ ${\displaystyle n}$- ${\displaystyle k}$ ${\displaystyle 2\ell \leqslant n-k$

증명. ${\displaystyle \mathrm{길이}}$의 버스트 패턴 $⩽{\displaystyle \leqslant \ell}$을(를) 수정할 수 있는 모든 선형 코드는 ${\displaystyle \mathrm{코드}}$ 워드로 길이의$$ 버스트${\displaystyle }$cannot$$ 2 cannot ${\displaystyle \leqslant 2\ell}$을(를) 가질 수 없다. 코드 워드로 길이$$${\displaystyle }$burst ${\displaystyle 2}$ ${\displaystyle \ell }$ ${\displaystyle \leqslant 2\ell }$이(가) 버스트인 경우, 길이 $\ell {\displaystyle }$ ${\displaystyle \$$ell$ $}$의 버스트 패턴 $\ell {\displaystyle }$ ${\displaystyle$ $\ell$$$}으로 변경될 수$$ 있으며$,$ 모든 코드 워드에서 길이$$ $\ell {\displaystyle }$ ${\\\displaystoper.$ 처음 ${\displaystyle 2}$㎛ {\$displaystyle 2\ell }$ 기호에$$ 벡터가 0이 아닌 경우, 벡터는 배열의 서로 다른 하위 집합에서 나와야 그 ${\displaystyle \mathrm{차이}}$가 길이 2㎛$${\$displaystyle 2\ell$}의 버스트의 코드 워드가 되지 않는다$.$ 이 조건을 확실히 하면, 그러한 하위 집합의 수는 최소한 벡터의 수와 같다. Thus, the number of subsets would be at least ${\displaystyle q^{2\ell }}$. Hence, we have at least ${\displaystyle 2\ell }$ distinct symbols, otherwise, the difference of two such polynomials would be a codeword that is a sum of two bursts of length ${\displaystyle \leqslant \ell .}$ Thus, this proves the Rie게르 바운드.

정의. 위의 리거 바운드를 달성하는 선형 버스트-오류-수정 코드를 최적 버스트-오류-수정 코드라고 한다.

버스트 오류 수정의 추가 범위

다중 단계 버스트 보정(MPBC)을 위해 선형 블록 코드의 달성 가능한 코드 속도에 대해 두 개 이상의 상한이 있다. 그러한 경계 중 하나는 모든 하위 블록 내에서 수정 가능한 최대 주기적 버스트 길이로 제한되거나, 동등하게 모든 단계 버스트 내의 최소 오차의 자유 길이 또는 간격에 대한 제약조건으로 제한된다. 이 바운드는 단일 버스트 보정을 위한 바운드의 특별한 경우로 축소되었을 때, 주기적 버스트 길이가 블록 길이의 절반 미만일 때 에이브람슨 바운드(버스트 오류 보정을 위한 해밍 바운드의 코럴)이다.^[3]

정리(버스트 수) For ${\displaystyle 1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1),}$ over a binary alphabet, there are ${\displaystyle n2^{\ell -1}+1}$ vectors of length ${\displaystyle n}$ which are bursts of length ${\displaystyle \leqslant \ell }$.^[1]

증명. 버스트 길이가 $⩽{\displaystyle }$ 1 ${\displaystyle \frac{2}{}}$( ${\displaystyle \mathrm{n}}$+ ${\displaystyle 1}$)${\displaystyle }$, ${\displaystyle \leqslant {\tfrac {1}{1$}:{2$}}(n+1$)이므로 버스트와 관련된 고유한 버스트 설명이 있다$$$.$ 버스트는 패턴의 $n{\displaystyle }$ ${\displaystyle n}$ 위치에서$$ 시작할 수 있다. 각 패턴은 $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$로 시작하며 $length$ ${\displaystyle \ell }$의 길이를 포함하고 있다$.$ $우리$는 1$${\$displaystyle \ell$}로$$ 시작하는 모든 문자열 $집합$으로 생각할 수 있다$.$ 따라서 ${\displaystyle {\ell }^{}}$- ${\displaystyle 1^{}}$ ${\$ 2$^{\ell$ -1$}$의 가능한 패턴이 있다.d a total of ${\displaystyle n2^{\ell -1}}$ bursts of length ${\displaystyle \leqslant \ell .}$ If we include the all-zero burst, we have ${\displaystyle n2^{\ell -1}+1}$ vectors representing bursts of length ${\displaystyle \leqslant \ell .}$

정리(암호어의 수에 대한 경계). If ${\displaystyle 1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1),}$ a binary ${\displaystyle \ell }$-burst error correcting code has at most ${\displaystyle 2^{n}/(n2^{\ell -1}+1)}$ codewords.

Proof. Since ${\displaystyle \ell \leqslant {\tfrac {1}{2}}(n+1)}$, we know that there are ${\displaystyle n2^{\ell -1}+1}$ bursts of length ${\displaystyle \leqslant \ell }$. Say the code has ${\displaystyle M}$ codewords, then there are ${\displaystyle Mn$는 부호 워드에서 길이 ⩽ ℓ{\displaystyle \leqslant \ell}의 붕괴로 다르2^{\ell)}}codewords. 각각의 M{M\displaystyle}, 말을 다른 코드 < 거맀을 것이며, 1{\displaystyle<1}은 별개가 되야 한다.따라서, M}⩽ 2n{\displaystyle M(2^{\ell)}+1)\leqslant 2^{n}(2ℓ − 1+1).$$ $M{\displaystyle }$ ${\displaystyle ⩽}$ ${\displaystyle {2n}^{}}$/${\displaystyle }$(${\displaystyle n}$ ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {\ell }^{}}$- ${\displaystyle 1^{}}$+ ${\displaystyle 1}$)${\displaystyle }$. ${\displaystyle M\leqslant 2^{n}/(n2^{\ell -1}+1$)을 암시한다$.$$}$

정리(Abramson의 한계). $1{\displaystyle \mathrm{}}$⩽${\displaystyle \ell }$ 1 2${\displaystyle }$(${\displaystyle \frac{\mathrm{n}}{}}$+ ${\displaystyle 1}$) ${\displaystyle 1\leqslant \ell$\leqslant \ell \$leqslant {\tfrac$ {1}{$1}:{2}}(n+$1)이 $이진$선형${\displaystyle n}$, k )이고${\displaystyle ,}$ ${\displaystystystyleyleyled(n, k),\ell$$$or) 오류 수정 코드)인 경우 블록 길이는 다음을 충족해야 한다.

${\displaystyle n\leqslant 2^{n-k-\ell +1}-1.}$

교정: 선형$({\displaystyle n}$, ${\displaystyle k}$) ${\displaystyle(n,k)}$ 코드의$$ 경우 2 ${\displaystyle k^{}}$ ${\$ 2$^{k}}$ 코드 워드가$$ 있다. 우리의 이전 결과에 의하면, 우리는

${\displaystyle 2^{k}\leqslant {\frac {2^{n}}{n2^{\ell -1}+1}}.}$

$n{\displaystyle }$ ${\displaystyle n}$을$($를) 분리하면 $n{\displaystyle }$ ${\displaystyle ⩽}$ ${\displaystyle {2n}^{}}$- ${\displaystyle k^{}}$ -${\displaystyle {\mathrm{\ell }}^{}}$+ 1${\displaystyle {}^{}}$- ${\displaystyle {\mathrm{}}^{}}$ -${\displaystyle {\mathrm{\ell }}^{}}$+ 1 ${\$1$}.$ $\ell {\displaystyle }$ ${\displaystyle ⩾}$ ${\displaystyle 1}$ ${\displaystyle \ell \geqslant$ 1$}$ 및$$ $n{\displaystyle }$ ${\displaystyle n}$은(는) 정수여야 하므로$$ $n{\displaystyle }$ ${\displaystyle ⩽}$ ${\displaystyle {2n}^{}}$- k -${\displaystyle {\ell }^{}}$+${\displaystyle {}^{}1}$ ${\displaystyle n\leqslant 2^{n-k-\ell$ +$1}-1}$가 있다$.$

비고. ${\displaystyle r}$= n${\displaystyle }$- ${\displaystyle k}$ ${\displaystyle r=n-k}$을(를) 코드의 이중화라고 하며$$, 에이브람슨의 한계에 대한 대체 공식에서는 $r{\displaystyle }$ ${\displaystyle ⩾}$ ${\displaystyle \lceil }$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}(n}$+ ${\displaystyle 1}$) ${\displaystyle +\ell }$- 1${\displaysty r\geqslant \log \{2}(n+1)\rceil +\ell-1}.$

화재코드^[3][4][5]

일반적으로 순환 코드는 버스트 오류를 감지하는 강력한 도구지만, 이제는 단일 버스트 오류 보정 기능이 우수한 Fire Code라는 이름의 이진 순환 코드 제품군을 고려한다. 단일 버스트(burst) 길이로 $말하면,$ 수신된 코드 워드가 가지고 있는 모든 오류는 $\ell {\displaystyle }$ ${\displaystyle \ell}$자리 고정$$ 범위 내에 있음을 의미한다.

${\displaystyle p}$( x${\displaystyle }$) ${\displaystyle p(x)}$을(를) ${\displaystyle {\mathrm{}}_{}}$ 2 ${\$$_{2$}}에$$ 대한 $ºm{\displaystyle }$ ${\displaystyle$ $m$$}$의 수정 불가능한 다항식이 되도록$$ 하고, $p{\displaystyle }$ ${\displaystyle$ p${\displaystyle \}}$을$x)$의 기간으로 한다$$$.$ The period of ${\displaystyle p(x)}$, and indeed of any polynomial, is defined to be the least positive integer ${\displaystyle r}$ such that ${\displaystyle p(x) x^{r}-1.}$ Let ${\displaystyle \ell }$ be a positive integer satisfying ${\displaystyle \ell \leqslant m}$ and $$${\displaystyle }$$2{\displaystyle }$ ▼${\displaystyle }$- ${\displaystyle 1}$ ${\$$displaystyle 2\ell -1}$ $여기$서 p ${\$${\displaystyle \mathrm{displaystyle}}$ p}은$($는$)$ $p{\displaystyle }$( x${\displaystyle }$) ${\displaystyle$ p$(x)}$의 기간$.$ 다음 발전기 다항식으로 Fire Code $G{\displaystyle }$ ${\$displaystyle G$}을 정의$하십시오.

${\displaystyle g(x)=\좌측(x^{2\ell -1}+1\우측)p(x).}$

$G{\displaystyle }$ ${\displaystyle G}$이(가) $\ell {\displaystyle }$ ${\displaystyle \ell}$ -burst-error$$ 수정 코드라는 것을 보여주겠다.

보조정리 1. $\\displaystyle \gcd \left(p(x),x^{2\ell -1}+1\right)=1.}$

증명. ${\displaystyle d}$( x${\displaystyle }$) ${\displaystyle d(x)}$을(를) 두 다항식 중 가장 큰 공통점이 되도록$$ 한다. Since ${\displaystyle p(x)}$ is irreducible, ${\displaystyle \deg(d(x))=0}$ or ${\displaystyle \deg(p(x))}$. Assume ${\displaystyle \deg(d(x))\neq 0,}$ then ${\displaystyle p(x)=cd(x)}$ for some constant ${\displaystyle$$c}$. But, ${\displaystyle (1/c)p(x)}$ is a divisor of ${\displaystyle x^{2\ell -1}+1}$ since ${\displaystyle d(x)}$ is a divisor of ${\displaystyle x^{2\ell -1}+1}$. 그러나 이는 $p{\displaystyle }$( x${\displaystyle }$) ${\displaystyle p(x)}$이(${\displaystyle 가}$) $x{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {\ell }^{}}$- 1${\displaystyle {}^{}}$+ ${\displaystyle x^{2\ell -1}+1.$따라서$$ ${\displaystyle \mathrm{deg}}$ ${\displaystyle }$ (${\displaystyle d}$)${\displaystyle }$= ${\displaystyle 0}$, ${\displaysty \deg(x)=0},$ {\d(으)}, 보조를 증명하는$$ 우리의 가정과 모순된다.

보조정리 2. $p{\displaystyle }$( ${\displaystyle x}$) ${\$$displaystyle p$$(x)}$이(${\displaystyle 가}$) period $p{\displaystyle }$ ${\displaystyle p}$의 다항식인 경우$,$ $p{\displaystyle }$(${\displaystyle }$x ) ${\displaystyle x{}^{}{k}^{}}$ - ${\displaystyle 1}$${\$$displaystyp p(x) x^{$$k}-$$1}$의 ${\displaystyle 경우}$에만${\displaystyle .}$

증명. $p{\displaystyle }$ ${\displaystyle k}$ ${\displaystyle$p$k}$인$$경우 ${\displaystyle x^{}}$ ${\displaystyle \mathrm{k}{}^{}}$- 1${\displaystyle }$=${\displaystyle }$( ${\displaystyle x^{}}$ ${\displaystyle \mathrm{p}{}^{}}$- 1${\displaystyle )(1}$+ ${\displaystyle x^{}}$ ${\displaystyle {}^{}}$+ ${\displaystyle {x\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle p^{}}$+${\displaystyle }$+${\displaystyle }$+ x${\displaystyle {}^{}}$/ ${\displaystyle p^{}}$)$${\$displaysty x$^{$k}-1=(x^{p}-1)(1+x^{p}+x^{2p}+\x^{k$/p$\}\}\}\}\}\}\}\}.$ 따라서 $p{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle x{}^{}}$ ${\displaystyle \mathrm{k}{}^{}}$- 1.${\displaystyle p(x)$ x$^{k}-1.$$}$

이제 $p{\displaystyle }$( ${\displaystyle x}$) x ${\displaystyle k^{}}$- ${\displaystyle 1}$ ${\displaystyle p(x)$ x$^{k}-1}$을(를) 가정해 봅시다$.$ $그러면{\displaystyle }$ k${\displaystyle p}$ p$${\$displaystyle k\geqslant p$ $k{\displaystyle }$ ${\displaystyle k}$은(으$)$에 대한$$ 유도에$$의해 p {\$displaystystystylease p}$에 의해 분리된다$$. 베이스 케이스 $k{\displaystyle }$= ${\displaystyle p}$ ${\displaystyle k=p$}이$($가) 그 뒤를$$ 따른다. 따라서 k> ${\displaystyle k>p}$을(를) 가정해 보십시오 p${\displaystyle }$( ${\displaystyle x}$) ${\displaystyle p(x)}$은(는) period p {\$displaystyp p}$이(가$)$ 있기 때문에) 두 가지를 모두 나눈다는$$ 것을 알고 있다$.$

${\displaystyle x^{p}-1=(x-1)\왼쪽(1+x+\ldots +x^{p-1}\ldots +x^{p-1}\right)\des {\text{and}-1=(x-1)\lift(1+x+\ldots +x^{k-1}\right)\right.}$

But ${\displaystyle p(x)}$ is irreducible, therefore it must divide both ${\displaystyle (1+x+\ldots +x^{p-1})}$ and ${\displaystyle (1+x+\ldots +x^{k-1})}$; thus, it also divides the difference of the last two polynomials, ${\displaystyle x^p(1+x+\dots +x^{p-k-1}}$${\displaystyle {}^{})}$ ${\displaystyle x^{p}(1+x+\ldots +x^{p-k-1}}$. Then, it follows that ${\displaystyle p(x)}$ divides ${\displaystyle (1+x+\cdots +x^{p-k-1})}$. Finally, it also divides: ${\displaystyle x^{k-p}-1=(x-1)(1+x+\ldots +x^{p-k-1})}$. By the induction hypothesis, ${$$\displaystyle$p$k-p$ 그 다음 ${\displaystyle p}$ k ${\displaystyle$ p $k$

${\displaystyle \mathrm{Leemma}}$ 2에 대한 유의점은 $p{\displaystyle }$( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle x^{}}$p - ${\displaystyle 1}$ ${\displaystyle p(x)=x^{p}-1}$이(가) 마침표 $p{\displaystyle }$ ${\displaystyle p}$이$($$가)$ 있기 때문에 p $k{\displaystyle }$${\displaystyle {}^{}}$-${\displaystyle }$${\displaystyle 1}$${\$$displaysty$ $x^{$$k}-$1}-1}을$($$가$$)$로 나눈다는 것이다$.$

정리. 방화 코드가 $is{\displaystyle }$ ${\displaystyle \ell}$ -버스트$$ 오류 수정^[4][5]

$모든{\displaystyle }$ 버스트 길이 length${\displaystyle \ell$} 이하가$$ 서로 다른 코세트에서 발생한다는 것을 보여줄 수 있다면, 우리는 그들을 수정 가능한 오류 패턴을 형성하는 코세트의 리더로 사용할 수 있다. 이유는 간단하다: 우리는 각각의 코셋이 그것과 관련된 독특한 신드롬을 가지고 있다는 것을 알고 있다. 그리고 만약 다른 길이의 모든 버스트가 다른 코셋에서 일어난다면, 모든 것이 독특한 신드롬을 가지고 있어서 오류 보정을 용이하게 한다.

정리 증명

Let ${\displaystyle x^{i}a(x)}$ and ${\displaystyle x^{j}b(x)}$ be polynomials with degrees ${\displaystyle \ell _{1}-1}$ and ${\displaystyle \ell _{2}-1}$, representing bursts of length ${\displaystyle \ell _{1}}$ and ${\displaystyle \ell$$_{2$}}: 각각 ${\displaystyle {with}_{}}$ 1,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}\ell }$. ${\displaystyle \ell$ \ell $_{1},\ell _{2}\leqslant \ell .}$ $정수$ i${\displaystyle ,}$ ${\displaysty i,j}$는 버스트의 시작 위치를 나타내며$$, 코드의 블록 길이보다 작다. 모순을 위해, x ${\displaystyle i}$ ${\displaystyle a^{}}$( x${\displaystyle }$) ${\displaystyle x^{i}a($${\displaystyle x}$$)}$와 x ${\displaystyle {}^{}}$( x${\displaystyle }$) ${\displaystyle$ x$^{j}b(x)}$가 동일한 코세트에 있다고$$ 가정한다. ${\displaystyle \mathrm{그러면}}$ $v{\displaystyle }$( x${\displaystyle }$)${\displaystyle }$= x ${\displaystyle i}$ ${\displaystyle a^{}}$ (${\displaystyle }$x${\displaystyle }$)${\displaystyle }$+ x ${\displaystyle j}$ ${\displaystyle b^{}}$( x${\displaystyle }$) ${\displaystyle v(x)=x^{i}a(x)+x^{j^{j(x$)}$b}}}}$는 유효한$$ 코드 워드(두 용어가 모두 동일한 코세트에 있으므로)이다. 일반성의 손실 없이, 나는 j{i\leqslant j\displaystyle}⩽. 분할 정리까지 − 나는 갈g(2ℓ − 1)+r, 정수 g{\displaystyle g}과 r, 0⩽ r<>2ℓ − 1{\displaystyler,0\leqslant r<, 2\ell)}에게{\displaystyle j-i=g(2\ell))+r,}. 우리는 다항식 v())을 고쳐 쓴{\와 같이 우리가:j 쓸 수 있다displ$aystyle v(x)}$은(는) 다음과 같다$$.

${\displaystyle v(x)=x^{i}a(x)+x^{i+g(2\ell -1)+r}=x^{i}a(x)+x^{i+g(2\ell -1)+r}+2x^{i+r}b(x)=x^{i}\left(a(x)+x^{b}b(x)\right)+x^{i+r}b(x)\left(x^{g(2\ell -1)}+1\right)}$

Notice that at the second manipulation, we introduced the term ${\displaystyle 2x^{i+r}b(x)}$. We are allowed to do so, since Fire Codes operate on ${\displaystyle \mathbb {F} _{2}}$. By our assumption, ${\displaystyle v(x)}$ is a valid codeword, and thus, must be a multiple of ${\displaystyle g(x}$${\displaystyle )}$ ${\displaystyle g(x$ 앞서 언급했듯이 $g{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle g(x)}$의 요인이 비교적 원시적이기$$ 때문에 v$$${\displaystyle }$( x${\displaystyle }$) ${\displaystyle v(x)}$은 x ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {\mathrm{x}}^{}}$ - ${\displaystyle 1^{}}$ + 1$(\displaystyle x^{2\$ell -1$}+$1}로$구분되어야 한다$ v${\displaystyle }$( ${\displaystyle x}$) ${\displaystyle v(x)}$에 대해 도출된 마지막 식을 자세히 살펴보면$$ x ${\displaystyle g^{}}$ ${\displaystyle {(2}^{}}$ ${\displaystyle {\ell }^{}}$- 1${\displaystyle {}^{}}$)${\displaystyle {}^{}}$+ 1 ${\displaystyle x^{g(2\ell -1)+1}+$1}는$$ x ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {\ell }^{}}$- ${\displaystyle 1{}^{}}$+ 1 $([displaysty style x^{2\$ell -1}+1}($Lema$)로 구분된다.$$ Therefore, ${\displaystyle a(x)+x^{b}b(x)}$ is either divisible by ${\displaystyle x^{2\ell -1}+1}$ or is ${\displaystyle 0}$. Applying the division theorem again, we see that there exists a polynomial ${\displaystyle d(x)}$ with degree ${\displaystyle \delta }$$$ 다음과 같은 경우:

${\displaystyle a(x)+x^{b^}b(x)=d(x)(x^{2\ell -1}+1)}$

그러면 우리는 다음과 같이 쓸 수 있다.

${\displaystyle {\ligned}\institutes +2\ell -1&=\lift \left(d(x)\left(x^{2\ell -1}+1\right)\right)\right)\\&=\lift(a(x)+x^{b(x)\right)\\&=\lift(x^{b(x)\right)&&\properties(a(x))=\ell _{1}-1<2\ell -1\\&=b+\ell _{2}-1\end{arged}}}$

이후 ℓ 1, ℓ 2⩽ ℓ{\displaystyle \ell_{1},\ell _{2}\leqslant \ell}우리는 단언할 수 있b ⩾ ℓ+는 b대리자를 암시하 δ,{\displaystyleb\geqslant \ell +\delta,}, ℓ − 1{\displaystyle b>, \ell)}양쪽의 학위 Equating.{\displaystyle b=2\ell -\ell_{2}+\delta.}b)2ℓ − ℓ 2+δ을 준다.그리고 > ${\displaystyle b}\delta$ 확장 시 주의할 점은:

${\displaystyle a(x)+x^{b^}b(x)=1+a_{1}x+a_{2}x^{2}+\ldots +x^{\ell _{1}-1}+x^{b}\왼쪽(1+b_{1}x+b_{2}}x^{2}+\ldots +x^{\ell _{2}-1}\오른쪽).}$

용어)b{\displaystyle x^{b}},지만 δ<>부터 b<>2ℓ − 1{\displaystyle \delta<>b<, 2\ell)}, 결과 식 d())(x2ℓ − 1+1){\displaystyle d())(x^{2\ell)}+1)}}, 따라서)0{\displaystyle d())=0}()) 해야 xb{\displaystyle x^{b}을 함유하고 있지 않는 것으로 보인다. 그리고 subsequly $a{\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$+ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle 0.}$ ${\displaystyle a(x)+x^{b(x)=0.}$$$ This requires that ${\displaystyle b=0}$, and ${\displaystyle a(x)=b(x)}$. We can further revise our division of ${\displaystyle j-i}$ by ${\displaystyle g(2\ell -1)}$ to reflect ${\displaystyle b=0,}$ that is ${\displaystyle j-i=g(2\$$el -1$ $v{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle v(x)}$로 다시 대체하면$$

${\displaystyle v(x)=x^{i}b(x)\왼쪽(x^{j-1}+1\오른쪽).}$

(( ) == - << ${\displaystyle \deg(b(x)))$$=\ell _{2}-1<\ell$ 는 deg ( ( )< ( ( )= ${\displaystyle \property($b$)(x$))가 있다.$<\deg(p(x)=m$ 그러나 ${\displaystyle p}$( x${\displaystyle }$) ${\displaystyle p(x)}$은(는) 수정할 수 없으므로$$ b${\displaystyle }$( ${\displaystyle x}$) ${\displaystyle b(x)}$ 및 p$$${\displaystyle }$( x${\displaystyle )}$ ${\displaystystyp(x)}$은(${\displaystyle x}$)}이(가) 비교적 프라임이어야 한다$$. $v{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle v(x)}$이(가) 암호어이므로$$ $x{\displaystyle {}^{}}$ ${\displaystyle {j\mathrm{}}^{}}$${\displaystyle {}^{}}$- 1${\displaystyle {}^{}}$+ ${\displaystyle 1}$ ${\displaystyle x^{j-1}+$1}은$($는) p${\displaystyle }$${\displaystyle {}^{}}$${\displaystyle }$( x${\displaystyle }$) ${\displaystyle p(x)}$로 구분할 수 없으므로 p ( ${\displaystyle x}$ ) ${\displaystylease$ x$^{2\line -1}+$1}+1$}+1$}로 구분해야 한다$$$.$ Therefore, ${\displaystyle j-i}$ must be a multiple of ${\displaystyle p}$. But it must also be a multiple of ${\displaystyle 2\ell -1}$, which implies it must be a multiple of ${\displaystyle n={\text{lcm}}(2\ell -1,p)}$ but that is precisely the block-length of the code. $따라서{\displaystyle }$ $j{\displaystyle }$- i ${\displaystyle j-i}$은(는) n ${\displaystyle n}$보다 작으므로$$ $n{\displaystyle }$ ${\displaystyle$ n$}$의 배수일 수 없다$$$.$ ${\displaystyle \mathrm{따라서}}$ $v{\displaystyle }$( x${\displaystyle }$) ${\displaystyle v(x)}$이(가) 코드 워드라는$$ 우리의 가정은 틀렸으며, $따라서{\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ i${\displaystyle }$(${\displaystyle x}$ )$${\$displaystyle$x^{$i}a(x)}$와 x${\displaystyle }$j ( ${\displaystyle x}$)$${\$displaysty$ x$^{j}b(x)}}}$은 서로 다른 코세트에 있으며, 따라서 수정 가능하다.

예: 화재 코드 수정 오류 5-버스트

위의 섹션에 제시된 이론과 함께 5 ${\displaystyle 5}$ -버스트$$ 오류 수정의 구성을 고려하십시오. 방화 코드를 구성하기 위해서는 우리 코드의 버스트 오류 수정 기능을 나타내는 수정 불가능한 다항식 p${\displaystyle }$( x${\displaystyle }$) ${\displaystyle p(x$ 정수 ℓ ${\displaystyle \ell }$이$($${\displaystyle 가}$) 필요하며, 2 ${\displaystyle \mathrm{\ell }}$- 1 ${\displaystyty 2\ell$ -1}이$$p의 기간으로 나눌 수 없는$$ 속성을 충족해야 한다는 것을 기억하십시오${\displaystyle .}$${\displaystyle p(x)}$. With these requirements in mind, consider the irreducible polynomial ${\displaystyle p(x)=1+x^{2}+x^{5}}$, and let ${\displaystyle \ell =5}$. Since ${\displaystyle p(x)}$ is a primitive polynomial, its period is ${\displaystyle 2^{$$5}-1=31$ 2 ${\displaystyle \ell }$- ${\displaystyle 1}$= ${\displaystyle 9}$ ${\displaystyle 2\ell -1=9}$이(가) ${\displaystyle 31}$ ${\displaystyle 31}$에 의해 분리되지 않음을 확인함$.$ 따라서,

${\displaystyle g(x)=(x^{9}+1)\왼쪽(1+x^{2}+x^{5)}\오른쪽)=1+x^{2}+x^{5}+x^{9}}+x^{11}+x^{14}}}}$

화재 코드 발생기야 $p{\displaystyle }$ ${\displaystyle p}$과 2 ${\displaystyle ³}$- ${\displaystyle 1}$ ${\displaystyle 2\ell -1}$의 최소 공통 배수를 평가하여 코드의 블록 길이를 계산할 수 있다$.$ 즉, n${\displaystyle }$= ${\displaystyle \text{lcm}(9,}$ ${\displaystyle 31}$)${\displaystyle }$= ${\displaystyle 279}$ ${\displaystyle$ n$={\lcm}(9,31)=279$ 따라서 위의 소방법은 길이 $[\displaystyle 5}$ 이하의$$ 버스트를 수정할 수 있는 주기 코드다.

바이너리 리드-솔로몬 코드

리드-솔로몬과 같은 특정 코드 패밀리는 이진수보다 큰 알파벳 크기로 작동한다. 이 특성은 그러한 코드의 강력한 버스트 오류 수정 기능을 부여한다. $F{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {{2m}^{}}_{}}$ ${\$에서 작동하는 코드를 생각해 보십시오$.$ 알파벳의 각 기호는 $m{\displaystyle }$ ${\displaystyle m}$비트로$$ 나타낼 수 있다. If ${\displaystyle C}$ is an ${\displaystyle (n,k)}$ Reed–Solomon code over ${\displaystyle \mathbb {F} _{2^{m}}}$, we can think of ${\displaystyle C}$ as an ${\displaystyle [mn,mk]_{2}}$ code over ${\displaystyle \mathbb {F} _{2}}$.

이러한 코드가 버스트 오류 보정에 강력한 이유는 $각{\displaystyle }$ 기호가 m ${\displaystyle m}$비트로$$ 표시되기 때문이며, 일반적으로 이러한 $m{\displaystyle }$ ${\displaystyle m}$비트의$$ 개수가 잘못되었든, 단일 비트 또는 모든 $m{\displaystyle }$ ${\displaystyle m}$비트에$$ 오류가 포함되어 있든, 디코딩적 관점에서 보면 i.s 단일 기호 오류. 즉, 버스트 오차는 군집 내에서 발생하는 경향이 있기 때문에, 여러 이진 오차가 단일 기호 오차의 원인이 될 가능성이 크다.

$({\displaystyle m}$+ ${\displaystyle 1}$) ${\displaystyle (m+1)}$개의$$ 오류가 최대 $2개$의 ${\displaystyle 2}$개의$$ 기호에 영향을 줄 수 있으며, ${\displaystyle \mathrm{2m}}$+ ${\displaystyle 1}$의 버스트 $유형 2m+1$}은$(는)$ 최대 $3개$의 ${\displaystystyle 3}$개의$$ 기호에 영향을 줄 수 있다는$$ 점에 유의하십시오. 그러면 t ${\displaystyle m}$+ ${\displaystyle 1}$ ${\displaystyle$ $tm+1$$}$$$버스트가 $최대{\displaystyle }$ t${\displaystyle }$+ ${\displaystyle 1}$ 기호에$$ 영향을 미칠 수 있으며$$$,$ 이는 $t{\displaystyle }$ ${\displaystyle t}$ - 심볼스-오류$$ 수정 코드가 최대 $({\displaystyle t}$- 1${\displaystyle }$) ${\displaystyle \mathrm{m}}$+ 1 ${\displaystyle (t-1)m+1}$ 길이로 버스트를 수정할 수 있음을 의미한다$.$

일반적으로 $F{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {{2m}^{}}_{}}$ ${\$$displaystyle t}$에 대한 Reed-Solomon 코드를 수정하는 오류$$ {\$displaystyle \mathb$ {$F} _{2^{m}}}}}$은(는) 모든 조합을 수정할 수 있다$$.

${\displaystyle {\frac {t}{1+\lfloor (l+m-2)/m\m\mloor }}}$

$t{\displaystyle }$ ${\displaystyle t}$을(를) 수정할 수 있는 것 외에 길이 $l{\displaystyle }$ ${\displaystyle l$의 버스트 수가 더 적음.

이진 RS 코드의 예

$G{\displaystyle }$ ${\displaystyle G}$을(를)${\displaystyle }$[${\displaystyle 255,}$ ${\displaystyle 223,}$ ${\displaystyle 33}$] ${\displaystyle [255,223,$33$]}$RS$$ 코드 F ${\displaystyle {{\mathrm{}}^{}}_{}}$ ${\displaystyle {{8\mathrm{}}^{}}_{}}$ ${\$ NASA에 의해 카시니-Hygens 우주선에 채용되었다.^[6] $\lfloor {\displaystyle }$ ${\displaystyle 33}$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle \rfloor }$= ${\displaystyle 16}$ ${\displaystyle \lfloor =16}$ 기호$$ 오류를 수정할 수 있다. 우리는 $이제{\displaystyle }$ G$${\$displaystyle G}$에서 Binary $RS{\displaystyle {}^{}}$ Code G$display$ {\$displaystyle$ G$'}$을(를) 생성한다. 각 기호는 $\lceil {\displaystyle }$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle }$(${\displaystyle 255)}$=${\displaystyle 8}$ {\$displaystyle \lceil \log _{2}(255)\rceil =8}$비트를$$ 사용하여 작성된다$.$ 따라서 바이너리 RS 코드는${\displaystyle \mathrm{파라미터}}$로${\displaystyle }$[${\displaystyle 2040}$,${\displaystyle 1784{}_{}}$ 33 ] ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}개가 될 것이다. 길이 $l{\displaystyle }$= ${\displaystyle 121}$ ${\displaystyle l=121}$의 단일 버스트를 수정할 수 있다$.$

인터리브 코드

인터리빙은 수녀원 코드를 임의 오류 수정기에서 버스트 오류 수정기로 변환하는 데 사용된다. 인터리브 코드 사용에 대한 기본적인 아이디어는 수신기에서 기호를 섞는 것이다. 이는 수신된 오류 버스트의 무작위화로 이어지며, 이는 가까운 위치에 있으며, 우리는 무작위 채널에 대한 분석을 적용할 수 있다. 따라서 송신기에서 인터리버가 수행하는 주요 기능은 입력 기호 시퀀스를 변경하는 것이다. 수신기에서 디인터리버는 수신된 시퀀스를 변경하여 송신기에서 원래 변경되지 않은 시퀀스를 되찾는다.

인터리버 용량 수정 중 버스트 오류 발생

정리. 일부 코드의 버스트 오류 수정 기능이 $\ell {\displaystyle }$, ${\displaystyle \ell ,}$인 경우, $\lambda {\displaystyle }$ ${\displaystyle \lambda$} -way$$ interleval은 ${\displaystyle \lambda .}$ ${\displaystyle \lambda \ell .}$이다.

Proof: Suppose that we have an ${\displaystyle (n,k)}$ code that can correct all bursts of length ${\displaystyle \leqslant \ell .}$Interleaving can provide us with a ${\displaystyle (\lambda n,\lambda k)}$ code that can correct all bursts of length ${\displaystyle \leqslant \lambda \ell$$,}$ for any given ${\displaystyle \lambda }$. If we want to encode a message of an arbitrary length using interleaving, first we divide it into blocks of length ${\displaystyle \lambda k}$. We write the ${\displaystyle \lambda k}$ entries of each block into a ${\displaystyle \lambda \times k}$ matrix using roh 그런 다음${\displaystyle }$(${\displaystyle n}$, ${\displaystyle k}$) ${\displaystyle (n,k)}$ 코드를$$ 사용하여 각 행을 인코딩한다. 우리가 얻을 것은 $\lambda {\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle n}$ ${\displaystyle \lambda \time n}$ 행렬이다$$. 자, 이 행렬은 열전주 순서로 읽혀지고 전송된다. 트릭은 전송된 단어에$$ $길이{\displaystyle }$ h ${\displaystyle h}$이(가) 버스트가 발생하는 경우 각 행에 약 $h{\displaystyle \frac{}{}}$ ${\$ {\$tfrac {h}{\lambda$}}} 연속$$ 오류가 발생한다는 것이다(더 구체적으로는 각 행에 길이 버스트 적어도 $\lfloor {\displaystyle }$ ${\displaystyle h\frac{}{}}$ ${\displaystyle \frac{\lambda }{}}$ ⌋ ${\displaystyle \rfloor }$ \ \ \$\$ \lflflflflflflpround ${\t${\t}{\t}{\lflflflflflack {\$fla$$.$$mbda }}\chloor }$ 및$$ 최대 $\lceil {\displaystyle }$ ${\displaystyle \frac{h}{}}$ ${\displaystyle \rceil }$ $\$ {\$displaystyle \lceil${\$tfrac$ {h$}{\lambda }}\rceil }).$ $h{\displaystyle }$ ${\displaystyle ⩽}$ ${\displaystyle \lambda \ell }$, {\$displaystyle$h\$leqslant \lambda$\ell $,}$인 ${\displaystyle \frac{\mathrm{경우}}{}}$ ${\displaystyle h}$ ${\displaystyle ⩽}$ ⩽ ⩽ { ${\displaystyle$ {h$}{\lambda$$}}}}}\displaystyle(n,k)$$$코드는${\displaystyle }$각 행을 수정할 수 있다. 만약 h입니다. 따라서 틈새 있는(λ,λ k){\displaystyle(n,\lambda k\lambda)}부호.;λ ℓ,{\displaystyle h>, \lambda \ell,} 다음 적어도 한줄}}h({\displaystyle{\tfrac{h}{\lambda}보다 더 많은 연속 오류를 포함할 것이며, 길이 h{h\displaystyle}의 폭발을 해결할 수 있습니다.그 ${\displaystyle (n}$, ${\displaystyle k}$) ${\displaystyle(n,k)}$ 코드가$$ 이 코드를 수정하지 못할 수 있음. 따라서$$ 인터리브$({\displaystyle \mathrm{\lambda n},}$ $){\displaystyle (\lambda n,\lambda$ k$)}$ 코드의$$ 오류 수정 능력은 정확히 ${\displaystyle \lambda }$. ${\displaystyle ..}${\$displaystyle \lambda \ell.}$ 인터리브 코드의 BEC 효율성은 원래${\displaystyle (n}$ ,${\displaystyle k}$ )$${\$displaystystylease (n,k)$ 코드와$$ 동일하다. 이는 다음과 같은 이유에서 사실이다.

${\displaystyle {\frac {2\fractda \ell \ell}{\proda n-\proda k}={\frac {2\ell}{n-k}}}}}}$

블록 인터리버

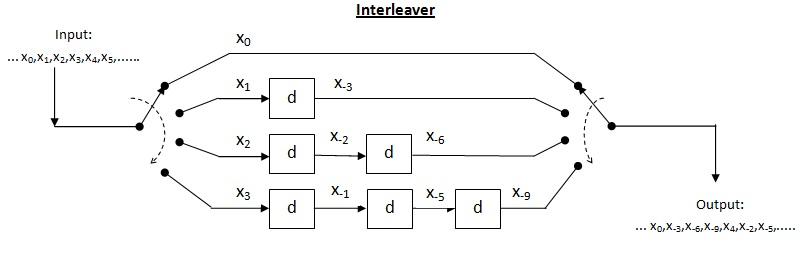
아래 그림은 가로 세로 3의 인터리버를 나타낸다.

위의 인터리버는 블록 인터리버라고 불린다. 여기서 입력 기호는 행에 순차적으로 쓰여지고 출력 기호는 열을 순차적으로 읽어 얻어진다. 따라서 이는 $M{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle N}$ ${\displaystyle M\time N}$ 배열의$$ 형태로 나타난다. 일반적으로 $N{\displaystyle }$ ${\displaystyle N}$은(는) 코드 워드의 길이입니다$$.

블록 인터리버 용량: For an ${\displaystyle M\times N}$ block interleaver and burst of length ${\displaystyle \ell ,}$ the upper limit on number of errors is ${\displaystyle {\tfrac {\ell }{M}}.}$ This is obvious from the fact that we are reading the output column wise and the number of rows is ${\displaystyle M}$. By th$위$의 정리${\displaystyle }$t$,$ {\$displaystyle t}$까지의 오류 보정 용량에 대해 허용되는 최대$$ 버스트 길이는 ${\displaystyle M}$ ${\displaystyle t}$ .${\displaystyle Mt.}$ M $t{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle Mt+1}$의 버스트 길이의 경우$$ 디코더가 실패할 수 있다$.$

블록 인터리버의 효율성(${\displaystyle }$ ${\displaystyle \gamma }$ ):$$ 디코더가 인터리버 메모리에 실패할 수 있는 버스트 길이의 비율을 취함으로써 발견된다. 따라서 $as{\displaystyle }$ ${\displaystyle \gamma}$을(를) as로$$ 공식화할 수 있다.

${\displaystyle \gamma ={\frac {Mt+1}{MN}\약 {\frac {t}{N}}.}$

블록 인터리버의 단점 : 그림에서 분명히 칼럼을 순차적으로 읽게 되므로 수신자는 완전한 메시지를 수신한 후에만 단일 행을 해석할 수 있고 그 전에는 해석하지 않는다. 또한 수신기는 수신한 기호를 저장하기 위해서는 상당한 양의 메모리가 필요하며, 완전한 메시지를 저장해야 한다. 따라서 이러한 요인은 두 가지 단점을 야기한다. 하나는 대기 시간이고 다른 하나는 저장 공간이다. (대단히 많은 양의 메모리)이다. 이러한 단점은 아래에 설명된 경련성 인터리버를 사용함으로써 피할 수 있다.

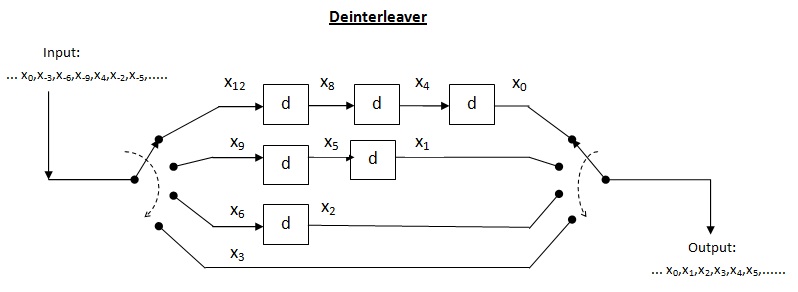
콘볼루션 인터리버

크로스 인터리버는 멀티플렉서-디멀티플렉서 시스템의 일종이다. 이 시스템에서 지연선은 점진적으로 길이를 증가시키기 위해 사용된다. 지연 라인은 기본적으로 신호를 특정 시간 지속시간까지 지연시키기 위해 사용되는 전자회로다. $n{\displaystyle }$ ${\displaystyle n}$을(를) 지연 라인의 수로 $하고{\displaystyle }$ d$${\$displaystyle d}$을(를) 각 지연 라인에 의해 도입된 기호의 수로 한다$$. 따라서 연속 입력 간의 구분 = $n{\displaystyle }$ ${\displaystyle d}$ ${\displaystyle nd}$ 기호$$ 코드 워드 ⩽${\displaystyle n}$. ${\displaystyle \leqslant n.}$ 따라서$$ 입력 코드 워드의 각 기호는 구별되는 지연 라인에 있게 된다. 길이 $\ell {\displaystyle }$ ${\displaystyle \ell }$의 버스트 오류가 발생하도록$$ 하십시오. 연속된 기호 간의 분리가 ${\displaystyle n}$ $d{\displaystyle }$, ${\displaystyle nd}$이므로, 디인터리브 출력에 포함될 수 있는 오류$$ 수는 $\ell n{\displaystyle \frac{}{}}$ ${\displaystyle \frac{d}{}}$+ ${\displaystyle \frac{1}{}}$. ${\displaystyle {\tfrac {\ell}{nd+1}.$$}$ 위 정리에서는$$ $t{\displaystyle }$ ${\displaystyle t}$까지의 오류 보정 용량에 대해 허용되는 최대 버스트 길이는${\displaystyle }$(${\displaystyle n}$ d${\displaystyle }$+ ${\displaystyle 1}$)${\displaystyle }$( ${\displaystyle t}$- ${\displaystyle 1}$)${\displaystyle }$. ${\displaystyle (nd+1)(t-1$)이다$.$$}$${\displaystyle }$(${\displaystyle n}$ ${\displaystyle d}$+ 1${\displaystyle }$)${\displaystyle }$( t${\displaystyle }$- ${\displaystyle 1}$)${\displaystyle }$+ ${\displaystyle 1}$, ${\displaystyle (nd+1)(t-1)+1,}$ 디코더의$$ 버스트$$ 길이가 실패할 수 있다.

크로스 인터리버의 효율성 (${\displaystyle }$ ${\displaystyle \gamma }$ ) $$: 디코더가 인터리버 메모리에 고장날 수 있는 버스트 길이의 비율을 취함으로써 발견된다. 이 경우 인터리버의 기억은 다음과 같이 계산할 수 있다.

${\displaystyle(0+1+2+3+\cdots +(n-1)d={\frac {n(n-1)}{2}}d.}$

따라서 다음과 같이$$ $\gamma {\displaystyle }$ ${\displaystyle \gamma}$을(를) 공식화할 수 있다.

${\displaystyle \cHB ={\frac {(nd+1)(t-1)+1}{{\frac {n(n-1)}{2}}d}}.}$

크로스 인터리버 성능 : 위의 인터리버 그림에서 보듯이 출력은 각 지연선 끝에서 생성되는 대각선 기호에 불과하다. 이 경우 입력 멀티플렉서 스위치가 절반 정도 전환되면 수신기에서 첫 번째 행을 읽을 수 있다. 따라서, 우리는 첫 번째 행을 읽기 위해서 수신기에 최대 반 쪽 메시지를 저장해야 한다. 이는 스토리지 요구사항을 절반으로 줄인다. 이제 첫 번째 행을 읽으려면 절반의 메시지만 필요하기 때문에 대기 시간도 절반으로 줄어 블록 인터리버에 비해 양호한 개선 효과를 볼 수 있다. 따라서, 총 인터리버 메모리는 송신기와 수신기 사이에서 분할된다.

적용들

컴팩트 디스크

코드를 수정하지 않으면 디지털 오디오는 기술적으로 실현 가능하지 않을 것이다.^[7] 리드-솔로몬 코드는 모든 비트가 잘못된 기호를 쉽게 수정할 수 있는 것처럼 단일 비트 오류로 손상된 기호를 수정할 수 있다. 따라서 버스트 오류를 수정하는 데 RS 코드가 특히 적합하다.^[5] 지금까지 RS코드의 가장 일반적인 적용은 컴팩트디스크에 있다. RS 코드에 의해 제공되는 기본적인 오류 수정 외에 크로스 인터리버에 의해 디스크의 긁힘으로 인한 버스트 에러로부터 보호가 제공된다.^[3]

현재의 컴팩트 디스크 디지털 오디오 시스템은 네덜란드의 N. V. 필립스와 일본의 소니사가 개발하였다(1979년 체결된 협정).

콤팩트 디스크는 투명한 플라스틱 코팅으로 코팅된 120mm 알루미늄 디스크로 구성되며, 길이 약 5km의 나선 트랙으로, 최대 0.25m/s의 일정한 속도로 파장 레이저에 의해 광학적으로 스캔된다. 이 일정한 속도를 달성하기 위해 트랙의 안쪽 부분에서 스캔하는 동안 디스크 회전 속도가 최대 8rv/s에서 바깥쪽 부분에서는 최대 3.5rv/s까지 다양하다. 구덩이와 착륙은 트랙을 따라 2진수 데이터를 구성하는 강하(깊이 0.12μm)와 평평한 세그먼트(0.6μm 폭)이다.^[8]

CD 프로세스는 다음 하위 프로세스의 시퀀스로 추상화될 수 있다: -> 신호 소스의 채널 인코딩 -> 마스터 디스크를 준비하고, 사용자 디스크를 만들고, 재생하는 동안 사용자 디스크에 내장된 신호를 감지하는 기계적인 하위 프로세스 – 채널 -> 사용자 디스크에서 감지된 신호 디코딩

이 과정은 버스트 오류와 무작위 오류가 모두 발생한다.^[7] 버스트 오류는 디스크 소재(알루미늄 반사필름의 결함, 투명한 디스크 소재의 반사율 불량), 디스크 생산(디스크 형성 및 디스크 절단 등의 결함), 디스크 취급(scratch - 일반적으로 얇은 레이디얼 및 녹음 방향과 직교하는 직교) 및 플레이백 메커니즘의 변화를 포함한다. 무작위 오류에는 재구성된 신호파의 지터와 신호의 간섭으로 인한 오류가 포함된다. CIRC(Cross-Interleaved Reed-Solomon code)는 CD 공정에서 오류 감지 및 보정을 위한 기반이다. 순차적으로 최대 3,500비트(CD 표면에 보이는 길이 2.4mm)의 버스트를 수정하고 사소한 스크래치로 인해 발생할 수 있는 최대 12,000비트(8.5mm)의 버스트를 보정한다.

인코딩: 음파는 A/D 컨버터에 의해 샘플링되고 디지털 형태로 변환된다. 음파는 진폭에 대해 샘플링된다(44.1kHz 또는 44,100 쌍으로, 스테레오 사운드의 좌우 채널에 대해 각각 하나씩). 인스턴스의 진폭에는 길이 16의 이진 문자열이 할당된다. 따라서 각 표본은 F ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {16}_{}^{}}$ ${\$ 또는$$ 4 F ${\displaystyle {\mathrm{}}_{}^{}}$ 8 ${\$바이트의$$ 데이터에서 2개의 이진 벡터를 생성한다. 녹음된 음의 매 초마다 44,100 × 32 = 1,411,200비트(176,400바이트)의 데이터가 나온다.^[5] 1.41 Mbit/s 샘플링된 데이터 스트림은 오류 수정 시스템을 통과하여 결국 1.88 Mbit/s의 스트림으로 변환된다.

인코더를 위한 입력은 24개의 8비트 기호로 구성된다(A/D 컨버터의 16비트 샘플 12개, 좌우 데이터(음향) 소스에서 각각 6개). A frame can be represented by ${\displaystyle L_{1}R_{1}L_{2}R_{2}\ldots L_{6}R_{6}}$ where ${\displaystyle L_{i}}$ and ${\displaystyle R_{i}}$ are bytes from the left and right channels from the ${\displaystyle i^{th}}$ sample of the frame.

처음에 바이트는 L ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ 3 ${\displaystyle {L\mathrm{}}_{}}$ ${\displaystyle {5\mathrm{}}_{}}$ R ${\displaystyle {}_{}{}_{}}$ R 3 ${\displaystyle {}_{}{}_{}}$ 3 ${\displaystyle {}_{}{}_{}}$ 3 ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {4\mathrm{}}_{}}$ ${\displaystyle {L\mathrm{}}_{}}$ ${\displaystyle {6\mathrm{}}_{}}$ R ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {}_{}{}_{}}$ 4 ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {6\mathrm{}}_{}}$ ${\$로 표현되는 새로운 프레임을 형성하도록 순열된다.$L_{5}R_{1}R_{3}R_{5}L_{2}L_{4}$$L_{6}R_{2}R_{4}R_{6}}$ 여기서$$ ${\displaystyle {Li}_{}{}_{}}$, R ${\displaystyle {}_{}}$ ${\$은(는) 2개의 간섭 프레임 후 프레임에서 i $t{\displaystyle {}^{}}$ ${\displaystyle h^{}}$ ${\$th$$$}}}}}}}}$왼쪽과 오른쪽 샘플을$$ 나타낸다.

다음으로, 이 24개의 메시지 기호는 $F{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {256}_{}}$ ${\$에 대한 RS 코드 축약인 C2(28,24,5) Reed-Solomon 코드를 사용하여 인코딩된다$.$ 최소 거리 5인 2오류 수정. 이렇게 하면 4바이트의 중복성이 추가되고, $P{\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ P ${\displaystyle {2\mathrm{}}_{}}$ ${\${1}P_${2$}}: 새로운 프레임을 형성한다$$: L ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {L\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {L\mathrm{}}_{}}$ ${\displaystyle {5\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {}_{}{}_{}}$ R 5 ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ P ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ 2 ${\displaystyle {}_{}{}_{}}$ 4 ${\displaystyle {L\mathrm{}}_{}}$ ${\displaystyle {6\mathrm{}}_{}}$ ${\displaystyle {R\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\$$L_{5}R_{1}R_{3}R_{5}P_{1}P_{1}P_{2}L_{2}L_{4}$$L_{6}R_{2}R_{4}R_{6$ . 그 결과 28개의 심볼 코드는 a(28.4) 교차 인터리버를 통과하여 28개의 인터리브 기호로 이어진다. 그런 다음 이러한 코드들은 C1(32,28,5) RS 코드를 통과하여 32개의 코드화된 출력 기호를 생성한다. 다음 코드 워드의 짝수 기호가 있는 코드 워드의 홀수 기호들을 추가로 재정렬하여 위의 4프레임 지연 인터리빙 후에도 여전히 존재할 수 있는 짧은 버스트를 분리한다. 따라서 매 24개의 입력 기호에 $대해{\displaystyle }$ R${\displaystyle }$= ${\displaystyle 24}$/ $(\displaystyle R=24/32})$를 제공하는 32개의 출력 기호가 있을 것이다$.$ 마지막으로 제어 및 표시 정보의 1바이트가 추가된다.^[5] 그 다음 33바이트 각각은 EFM(814 변조)과 3개의 병합 비트를 추가하여 17비트로 변환된다. 따라서 6개 샘플의 프레임은 33바이트 × 17비트(561비트)를 생성하며, 여기에 24개의 동기화 비트와 3개의 병합 비트가 추가되어 총 588비트가 생성된다.

디코딩: CD 플레이어(Circ 디코더)는 32개의 출력 기호 데이터 스트림을 수신한다. 이 하천은 디코더 D1을 먼저 통과한다. 디코딩 방법을 결정하고 제품 성능을 최적화하는 것은 CD 시스템의 개별 설계자들의 몫이다. 최소 거리 5 D1, D2 디코더는 각각 $e{\displaystyle }$ $e}$$오류$ 및 $f {\displaystyle$ $f$$}$$오류$의 조합을 수정할 수 있으며$,$ 의 솔루션에서 D1은 단일 오차를 수정하도록 설계되어 있다^[5] 그리고 1개 이상의 오류가 발생할 경우 이 디코더는 28개의 지우개를 출력한다. 다음 단계에서 디인터레버는 28개의 D2 암호에 걸쳐 이러한 지우개를 분배한다. 다시 대부분의 솔루션에서 D2는 삭제(간단하고 비용이 적게 드는 솔루션)만을 다루기로 되어 있다. 4개 이상의 소거가 발생하는 경우 D2에 의해 24개의 소거가 출력된다. 그 후 오류 은폐 시스템은 수정할 수 없는 기호의 경우 보간(주변 기호로부터)을 시도하며, 그러한 잘못된 기호에 해당하는 소리가 음소거된다.

CERC의 성능:^[7] CERC는 단순한 선형 보간법으로 긴 버스트 오류를 은폐한다. 2.5mm의 트랙 길이(4000비트)는 수정 가능한 최대 버스트 길이, 7.7mm 트랙 길이(1만2300비트)는 보간할 수 있는 최대 버스트 길이다. 표본 보간률은 비트 오류율(BER) =${\displaystyle {10}^{}}$ -${\displaystyle 4^{}}$에서 10시간마다 1회, BER = ${\displaystyle {10}^{}}$ - 3 ${\$= $10^{-4},$ 분당$$ 1000회 샘플링 = 10${\displaystyle {}^{}}$- ${\displaystyle 3^{}}$ ${\$$^{-3} 검출$ 불가능한$$ 오류 샘플(클릭): ${\displaystyle {\mathrm{750시간}}^{}}$마다${\displaystyle {\mathrm{1회}}^{}}$ 미만, BER$$ = ${\displaystyle {10}^{}}$ - 3 ${\$ styleankset 10-daystyledaystyledaystypecastyledaystyleepecastyledaystyle${\displaystyle {-}^{}}$ 4 ${\$

참고 항목

• 오류 감지 및 수정
• 피드백을 사용하여 코드 오류 수정
• 코드 레이트
• 리드-솔로몬 오차 보정

참조