소거코드

코딩 이론에서 소거 코드는 비트 소거(비트 오류보다는)를 가정하는 전방 오류 보정(FEC) 코드로, k 기호의 메시지를 n 기호로 긴 메시지(코드 워드)로 변환하여 원본 메시지를 n 기호의 서브셋에서 복구할 수 있다. r = k/n 분수를 코드 레이트라고 한다. k'가 회수에 필요한 기호의 수를 나타내는 fraction k'/k를 수신 효율이라고 한다.

최적 삭제 코드

최적 삭제 코드는 n 코드 단어 기호 중 k가 원본 메시지를 복구하기에 충분한 속성을 가지고 있다(즉, 최적의 수신 효율을 가지고 있다). 최적의 삭제 코드는 분리 가능한 최대 거리 코드(MDS 코드)이다.

패리티 조회

패리티 검사는 n = k + 1. k 값 집합에서 다음과 같은 ${\displaystyle {특별}_{}}$한 경우. k 값${\displaystyle }${${\displaystyle {vi}_{}}$ ${\displaystyle {}_{}{}_{}}$ 1${\displaystyle {}_{}}$≤ ${\displaystyle i_{}}$ ${\displaystyle {\le }_{}}$ i ≤ ${\displaystyle k_{}}$ ${\$ 체크섬을 계산하여 k 소스 값에 추가한다.

${\displaystyle v_{k+1}=-\sum _{i=1}^{k}v_{i}.}$

k + 1 값${\displaystyle }${${\displaystyle {}_{}}$ ${\displaystyle i_{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {\le }_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {\le }_{}}$ ${\displaystyle {\mathrm{k}}_{}}$+ 1 ${\$의 집합은 이제 체크섬과 관련하여 일치한다$$. 이러한 값 중 ${\displaystyle {하나}_{}}$인 $v{\displaystyle {}_{}}$e {\$displaystyle v_{e}$을(를$)$ 지우면 나머지 변수를 합하면 쉽게 복구할 수 있다.

${\displaystyle v_{e}=-\sum _{i=1,i\neq e}^{k+1}v_{i}.}$

다항식 오버샘플링

예: 오류 메일(k = 2)

k = 2인 간단한 경우, 두 개의 원래 기호 사이의 선을 따라 다른 점을 샘플링하여 중복 기호를 생성할 수 있다. 이를 에러메일(err-mail:

앨리스는 자신의 전화번호(555629)를 에러메일로 밥에게 보내고 싶어한다. 에러메일은 이메일처럼 작동한다.

1. 모든 메일의 절반 가량이 분실된다.^[1]
2. 5자 이상 메시지는 불법이다.
3. 매우 비싸다(항공우편과 비슷하다.

앨리스는 밥에게 자신이 보내는 메시지를 인정해 달라고 부탁하는 대신 다음과 같은 계획을 구상한다.

1. 그녀는 자신의 전화번호를 a = 555, b = 629 두 부분으로 나누고, "A=555"와 "B=629"라는 두 개의 메시지를 밥에게 보낸다.
2. She constructs a linear function, ${\displaystyle f(i)=a+(b-a)(i-1)}$, in this case ${\displaystyle f(i)=555+74(i-1)}$, such that ${\displaystyle f(1)=555}$ and ${\displaystyle f(2)=629}$.

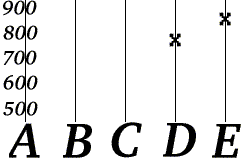
1. 그녀는 f(3), f(4), f(5) 값을 계산한 다음, 세 개의 중복 메시지인 "C=703", "D=777", "E=851"을 전송한다.

밥은 f(k)의 형태가 f${\displaystyle }$( ${\displaystyle i}$)${\displaystyle }$= ${\displaystyle a}$+${\displaystyle }$( ${\displaystyle b}$- a${\displaystyle }$)${\displaystyle }$( ${\displaystyle \mathrm{i}}$- ${\displaystyle 1}$) ${\displaystyle f(i)=a+(b-a)(i-1$이며 여기서 a와 b는 전화번호의 두 부분이라는 것을 알고 있다. 이제 밥이 "D=777"과 "E=851"을 받았다고 가정하자.

밥은 자신이 받은 값(f(4)과 f(5)에서 a와 b의 값을 계산하여 앨리스의 전화번호를 재구성할 수 있다. 밥은 어떤 두 개의 에러메일을 사용하여 이 절차를 수행할 수 있으므로, 이 예에서 삭제 코드의 비율은 40%이다.

앨리스는 6개의 문자를 포함하고 있기 때문에 하나의 에러메일로 전화번호를 인코딩할 수 없으며, 하나의 에러메일 메시지의 최대 길이는 5개라는 점에 유의하십시오. 만일 그녀가 조각조각으로 그녀의 전화번호를 밥에게 각 작품의 수령을 인정하라고 요구한다면, 어쨌든 적어도 네 개의 메시지가 전송되어야 할 것이다(앨리스로부터 두 개, 밥으로부터 두 개의 답장이 전송). 따라서 5개의 메시지가 필요한 이 예시에서의 삭제 코드는 상당히 경제적이다.

이 예는 약간 꾸며낸 것이다. 모든 데이터 집합에서 작동하는 정말로 일반적인 삭제 코드에 대해, 우리는 주어진 f(i)가 아닌 다른 것이 필요할 것이다.

일반사례

위의 선형 구조는 다항식 보간법으로 일반화할 수 있다. 또한, 점들은 이제 유한한 분야에 걸쳐 계산된다.

먼저 우리는 최소 n의 순서로 유한 필드 F를 선택하지만, 보통 2의 검정력을 선택한다. 송신자는 데이터 기호의 번호를 0에서 k - 1로 매기고 전송한다. 그런 다음 p(i)가 데이터 기호 i와 같도록 순서 k의 (Lagrange) 다항식 p(x)를 구성한다. 그런 다음 p(k), ..., p(n - 1)를 보낸다. 수신자는 k 기호를 성공적으로 수신할 경우 이제 다항식 보간법을 사용하여 손실된 패킷을 복구할 수 있다. F의 순서가 2보다^b 작을 경우, 여기서 b는 기호의 비트 수인 경우 다중 다항식을 사용할 수 있다.

송신자는 k에서 n - 1까지의 기호를 구성할 수 있다. 즉, 기호의 전송 사이에 작업량을 균등하게 분배한다. 수신자가 '즉시' 계산을 하려면, 기호 i < k가 성공적으로 수신된 경우 q(i) = p(i) 그리고 기호 i < k가 수신되지 않은 경우 q(i) = 0과 같은 새로운 다항식 q를 구성할 수 있다. 이제 r(i) = p(i) - q(i)로 하자. 첫째로 우리는 r(i) = 기호 i < k가 성공적으로 수신된 경우 0이라는 것을 안다. 둘째, 기호 i ≥k가 성공적으로 수신된 경우 r(i) = p(i) - q(i)를 계산할 수 있다. 그래서 우리는 R을 구성하고 손실된 패킷을 찾기 위해 그것을 평가하기에 충분한 데이터 포인트를 가지고 있다. 그래서 송신자와 수신자 모두 '즉시' 운용을 위해서는 O(n (n - k) 운용이 필요하며 O(n - k) 공간만 필요하다.

실제 구현

이 프로세스는 리드-솔로몬 코드에 의해 구현되며, Vandermonde 매트릭스를 사용하여 유한한 필드에 걸쳐 코드 단어가 구성된다.

최적에 가까운 삭제 코드

거의 최적에 가까운 삭제 코드는 (1 + ε)k 기호가 있어야 메시지를 복구할 수 있다(여기서 ε>0). ε 감소는 CPU 시간 비용으로 할 수 있다. 계산 복잡성에 대한 거의 최적의 삭제 코드 거래 보정 기능: 실제 알고리즘은 선형 시간 복잡성으로 인코딩 및 디코딩할 수 있다.

분수 코드(무임률 삭제 코드라고도 함)는 최적에 가까운 삭제 코드의 주목할 만한 예다. 그들은 k 기호 메시지를 사실상 무한히 인코딩된 형태로 변환할 수 있다. 즉, 오류 수정에 모두 사용될 수 있는 임의의 양의 중복 기호를 생성할 수 있다. 수신기는 암호화된 기호보다 약간 더 많이 수신한 후에 해독을 시작할 수 있다.

재생 코드는 기존 인코딩된 조각에서 인코딩된 조각이 손실된 재구축(수리라고도 함) 문제를 다룬다. 이 문제는 암호화된 이중화를 유지하기 위한 통신이 문제가 되는 분산형 스토리지 시스템에서 발생한다.

스토리지 시스템의 삭제 코딩 적용

스토리지 시스템의 장애로부터 복구하는 일반적인 방법은 복제를 사용하는 것이었습니다.^[2] 그러나 복제는 낭비된 바이트의 측면에서 상당한 오버헤드를 초래한다. 따라서 데이터 센터에서 사용되는 스토리지 시스템과 같이 점점 더 큰 스토리지 시스템이 삭제 코딩된 스토리지를 사용하게 된다. 스토리지 시스템에 사용되는 삭제 코딩의 가장 일반적인 형태는 패리티 블록이라고 불리는 알려진 데이터의 조각에서 누락된 데이터를 재생성하는 데 사용되는 고급 수학 공식인 리드-솔로몬(RS) 코드다.^[3] a (k, m) RS 코드에서는 "청크"라고 불리는 k 데이터 블록의 집합이 (k + m) 청크로 인코딩된다. 총 청크 세트는 스트라이프로 구성되어 있다. 코딩은 (k + m) 청크 중 적어도 k가 가능한 한 전체 데이터를 복구할 수 있도록 한다. 즉, (k, m) RS 인코딩 스토리지는 최대 m의 장애를 허용할 수 있다.

예: 자신의 HDFS를 위해 페이스북에서 사용되는 RS(10, 4) 코드에서는 10MB의 사용자 데이터를 10개의 1MB 블록으로 나눈다.^[4] 그런 다음 4개의 1MB 패리티 블록을 추가로 생성하여 이중화를 제공한다. 이것은 최대 4개의 동시 실패를 허용할 수 있다. 이곳의 스토리지 오버헤드는 14/10 = 1.4X이다.

완전히 복제된 시스템의 경우 최대 4개의 동시 실패를 허용하려면 10MB의 사용자 데이터를 4번 복제해야 한다. 이 경우 스토리지 오버헤드는 50/10 = 5배일 것이다.

이를 통해 삭제 코딩 스토리지의 스토리지 오버헤드가 전체 복제에 비해 낮다는 것을 알 수 있으며, 따라서 오늘날의 스토리지 시스템의 매력도 높일 수 있다.

예

다음은 다양한 코드 구현의 몇 가지 예:

최적 삭제 코드 근사치

• 토네이도 코드
• 저밀도 패리티 검사 코드

최적 분수에 가까운 코드(무속 삭제)

• 분수코드
• 온라인 코드
• LT 코드
• 랩터 코드
• 네트워크 코드

최적 삭제 코드

• 패리티: RAID 스토리지 시스템에 사용됨
• 파치브
• Tahoe-LAFS는 zfec을 포함한다.
• 리드-솔로몬 코드
• 최대 중복 패킷 수에서 MDS 코드가 Reed-Solomon을 능가하는 삭제 복원 체계 코드(Erase Resilient System Code)는 RS(4,2), RS(9,2)(3비트)를 참조하십시오.
• 코드^[5] 재생성에는 Storage Wiki도 참조하십시오.
• 기타 모든 MDS 코드("최대 거리 분리 가능 코드"의 일종)

기타

• 철자 알파벳

참고 항목

• 전달 오류 수정 코드.
• 비밀 공유(디코딩 쿼럼에 도달할 때까지 원래 비밀이 암호화되고 가려진다는 점에서 삭제)

참조

외부 링크

• Jerasure는 SIMD 최적화를 통해 Reed-Solomon 및 Cauchy 삭제 코드 기법을 구현하는 무료 소프트웨어 라이브러리다.
• Luigi Rizzo에 의한 컴퓨터 통신에서의 소프트웨어 FEC는 최적의 삭제 보정 코드를 설명한다.
• Feclib는 밴드 매트릭스를 사용하는 루이지 리조의 작품에 대한 거의 최적의 확장이다. 밴드의 폭 크기, 유한장의 크기처럼 많은 파라미터를 설정할 수 있다. 그것은 또한 현대 CPU의 큰 레지스터 크기를 성공적으로 이용했다. 위에서 언급한 최적 코드에 가까운 코드와 어떻게 비교하는지는 알 수 없다.
• 코드 재생성 및 삭제 코드 재구성을 위한 분산 스토리지 Wiki에 대한 코드 지정
• 1996년 개발된 ECIP "삭제코드 인터넷 프로토콜"은 인터넷에서 FEC "Forward Error correction"을 처음으로 사용한 것이다. 그것은 처음에 아서 C경의 라이브 비디오를 스트리밍하기 위해 상업적으로 사용되었다. 스리랑카에서 인디애나 UIUC로 클라크.