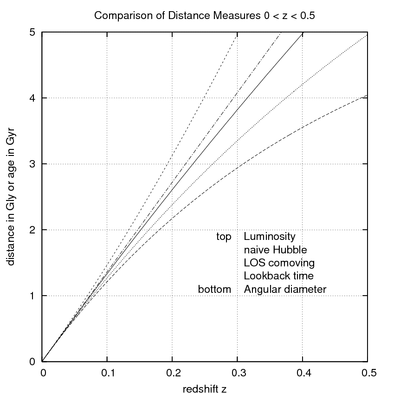
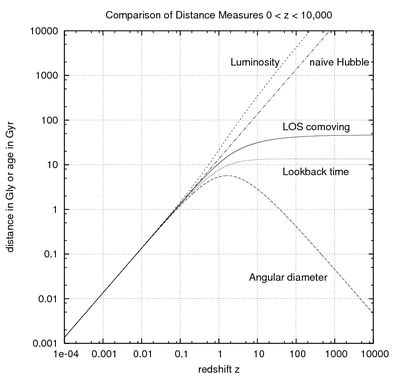
거리 측정(우주론)

코모빙(Comoving)과 적정 거리를 이 기사로 통합하자는 의견이 제시되었다. (토론) 2021년 1월부터 제안.

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "거리 측정" 우주론 – 뉴스 · 신문 · 책 · 학자 · JSTOR (2018년 4월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

다음에 대한 시리즈 일부
물리 우주론
빅뱅 · 우주 우주의 시대 우주의 연대기
초기 우주 인플레이션 · 핵합성법 배경 중력파(GWB) 마이크로파(CMB) · 중성미자(CNB)
확장 · 미래 허블의 법칙 · 레드시프트 공간의 미터법 확장 FLRW 미터법 · 프리드만 방정식 비균질 우주론 팽창하는 우주의 미래 우주의 궁극적 운명
구성요소 · 구조 구성 요소들 람다-CDM 모델 암흑 에너지 · 다크 유체 · 암흑 물질 구조 우주의 모양 은하 필라멘트 · 은하 형성 대형 퀘이사군 대규모 구조 재이온화 · 구조형성
실험 블랙홀 이니셔티브(BHI) 부머안그 우주 배경 탐색기(COBE) 암흑 에너지 조사 일러스트리스 프로젝트 플랑크 우주전망대 SDSS(Sloan Digital Sky Survey) 2dF 갤럭시 레드시프트 조사("2dF") 윌킨슨 마이크로파 비소트로피 프로브(WMAP)
과학자들 아론손 알펜 앨퍼 바라드와이 코페르니쿠스 시터 디케 엘러스 아인슈타인 엘리스 프리드만 갈릴레오 가모우 구스 호킹 허블 레마슈트레 매더 뉴턴 펜로즈 펜지아스 루빈 슈미트 평활 순체프 선야예프 톨먼 윌슨 젤도비치 우주론자 목록
제목이력 우주 전자레인지 발견 백그라운드 방사선 빅뱅 이론의 역사 에 대한 종교적인 해석 빅뱅 이론 우주론 연표
카테고리 천문 포털
v t

거리 측정은 물리적인 우주론에서 두 물체 사이의 거리나 우주의 사건 사이의 거리에 대한 자연스러운 개념을 주기 위해 사용된다. 그것들은 종종 관측 가능한 양(예: 원거리 퀘이사의 광도, 원거리 은하의 적색 편향 또는 우주 마이크로파 배경(CMB) 전력 스펙트럼의 음향 피크의 각도 크기)을 직접 관측할 수는 없지만 계산에 더 편리한 다른 양(예: 혼성 coo)에 묶는 데 사용된다.퀘이사 은하 등)의 좌표. 여기서 논의된 거리 측정은 모두 낮은 적색 임시방편에서의 유클리드 거리라는 일반적인 개념으로 줄어든다.

우주론에 대한 우리의 현재의 이해와 일치하여, 이러한 척도는 일반 상대성 이론의 맥락 안에서 계산되며, 여기서 프리드만-레마슈트레-로베르톤-워커 솔루션은 우주를 묘사하는 데 사용된다.

개요

우주론에서 "거리"에 대한 몇 가지 다른 정의가 있는데, 이 정의들은 모두 작은 적색 편향에 대해 점증적이지 않은 것이다. 이러한 거리에 대한 표현은 $적색편향{\displaystyle }$ z ${\displaystyle z}$의 함수로 쓰일 때 가장 실용적이다$.$ 적색편향은 항상 관측 가능하기 때문이다. 또한 축척 계수 $a{\displaystyle }$= ${\displaystyle 1}$/${\displaystyle }$( 1${\displaystyle }$+ ${\displaystyle z}$)${\displaystyle }$. ${\displaystyle a=1/(1+z$)의 함수로 쓸 수 있다$.$$}$

사실 적색선물에는 두 가지 개념이 있다. 하나는 우주 극초단파 배경에서 정의한 것처럼 지구와 물체가 모두 "커밍" 환경(허블 흐름)에 대해 움직이지 않는다면 관찰될 적색 편향이다. 다른 하나는 실제 적색 편향 측정으로 관찰된 물체의 고유 속도와 우리의 고유 속도에 따라 달라진다. 태양계가 약 370km/s에서 Leo와 Crater $사이$의 방향으로 이동하기 때문에, 이것은 그 방향의 먼 물체의 경우$$${\displaystyle 약}$ 1.$0012배$ 감소하고 반대 방향의 먼 물체에 대해서는 $동일$한 계수만큼 증가시킨다$.$ (태양 주위를 도는 지구의 운동 속도는 30km/s에 불과하다.)

우리는 먼저 몇 가지 거리 측정에 대한 공식을 제공하고, 그 다음 더 아래쪽에 자세히 기술한다. "허블 거리"를 다음과 같이 정의

${\displaystyle d_{H}={\frac {c}{H_{0}}}\약 3000h^{-1}{\text{Mpc}\약 9.26\cdot 10^{25}h^{1}{\text{m}}}}}}}}}}$

여기서 $c{\displaystyle }$ ${\displaystyle c}$은 빛의 속도, ${\displaystyle {H\mathrm{}}_{}}$ $0{\displaystyle {}_{}}$ ${\$은 오늘날$$ 허블 매개변수, h는 치수 없는 허블 상수로, 모든 $거리$는 z${\displaystyle {}_{}}$ d ${\displaystyle H_{}}$ ${\$ z$\cdot d_{{}$에 점증상이다.스몰 z용 $H}$

우리는 또한 차원 없는 허블 매개변수를 정의한다.^[1]

${\displaystyle E(z)={\frac {H(z)}{H_{0}}}={\sqrt {\오메가_{r}(1+z)^{4}+\오메가_{m}(1+z)^{3}+\오메가_{k}(1+z)^{2}+\오메가_{\Lambda }}}}}}}}}}}}}}}}}}}}}}}}}}:{\오메가.$

Here, ${\displaystyle \Omega _{r},\Omega _{m},}$ and ${\displaystyle \Omega _{\Lambda }}$ are normalized values of the present radiation energy density, matter density, and "dark energy density", respectively (the latter representing the cosmological constant), and ${\displaystyle {\mathrm{\Omega }}_k=1-{\mathrm{\Omega }}_r-{\mathrm{\Omega }}_m-{\mathrm{\Omega }}_{\mathrm{\Lambda }}}$${\displaystyle \Oomega_{k}=1-\Oomega_{r}-\Oomega_{m}-\Oomega_{\Lambda }}}}}}}$이(가) 곡률을 결정한다$$. 주어진 적색변환에서 허블 파라미터는 $H{\displaystyle }$( ${\displaystyle z}$)${\displaystyle }$= H ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$( $){\displaystyle H(z)=$이다.$H_{0}E(z)}$.

대부분의 다른 공식의 기초가 되는 거리 혼합식은 적분을 포함한다. 일부 제한된 매개변수 선택(아래 참조)의 경우, 혼합 거리 적분은 일반적으로 폐쇄 분석 형태를 가지지만, 특히 우리 우주의 매개변수에 대해서는 숫자적으로만 해결책을 찾을 수 있다. 우주학자들은 일반적으로 관찰자에서 적색편향 $z{\displaystyle }$ ${\displaystyle z}$의 가시선(LOS)을 따라$$ 물체까지의 거리에 대해 다음과 같은 측정법을 사용한다.^[2]

• 단거리:

${\displaystyle d_{C}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{E(z')}}}}}}$

There is a closed-form expression for this integral if ${\displaystyle \Omega _{r}=\Omega _{m}=0}$ or, by substituting the scale factor ${\displaystyle a}$ for ${\displaystyle 1/(1+z)}$, if ${\displaystyle \Omega _{\Lambda }=0}$. 현재 우리 우주는 $\Omega {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle r_{}}$= ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle k_{}}$= ${\displaystyle 0.}$ ${\displaystyle \Oomega _{r}=\Oomega _{k}=0.}$로 밀접하게 표현되고 있는 것 같다$$. 이 경우, 우리는 다음과 같은 것을 가지고 있다.

${\displaystyle d_{C}(z)=d_{H}\Omega _{m}^{-1/3}\Omega _{\Lambda }^{-1/6}[f((1+z)(\Omega _{m}/\Omega _{\Lambda })^{1/3})-f((\Omega _{m}/\Omega _{\Lambda })^{1/3})]}$

어디에

${\displaystyle f(x)\equiv \int _{0}^{x}{\frac {dx}{\sqrt{x^{3}+1}:{\displaysty \frac {dx}{\sqrt{x^}}+1}$

접근 거리는 물체나 우리가 특정한 속도를 가지고 있지 않을 경우 지속되는 z 값을 사용하여 계산해야 한다.

스케일 팩터와 함께 적절한 시간 거리를 제공한다.

${\displaystyle d=ad_{C}$

• 횡방향 접근 거리:

${\displaystyle d_{M}(z)={\begin{case}{\fract {d_{{}H}{{\sqrt{{k}}}\sinh \좌측({\frac {{\sqrt{\}}{k}d_{C}(z)}{d_{H}}\우측)&#&#160;\오메가 _{k}0\\d_{C}(z)&\오메가 _{k}=0\\\\frac {d_{\frac}{{d_}}H}}{{\sqrt{{k}}}}\sin({\frac {{\sqrt{\}}}\Oomega_{k}}{C}(z)}{d_{H}}\right)&#&###################################################\Oomega _{k}<0\end{case}}}$

• 각도 직경 거리:

${\displaystyle d_{A}(z)={\frac {d_{M}(z)}{1+z}}}}$

이 공식은 태양계도 물체도 그들 사이의 선에 평행한 독특한 속도 성분을 가지고 있지 않다면 엄격히 정확하다. 그렇지 않으면, 이 경우에 해당되는 빨간색 시프트를 사용해야 하지만 ${\displaystyle d_{}}$ $A{\displaystyle {}_{}}$ ${\$$A}}$은(는) 방향에 따라 0.99867~1.00133 사이의 인수로 태양계 운동을 보정해야 한다$$. (만약 어떤 물체를 향해 속도 v로 이동하기 시작하면, 어떤 거리에서도 그 물체의 각도 직경은 $({\displaystyle \sqrt{1}}$+ v${\displaystyle \sqrt{}}$/ ${\displaystyle \sqrt{c}}$)${\displaystyle \sqrt{}}$/ (${\displaystyle \sqrt{1}}$- v /${\displaystyle \sqrt{}}$)${\displaystyle \sqrt{}}$.${\displaystyle {\sqrt {(1+v/c)/(1-v/c)}$의 인수만큼 감소한다.$}$)

• 조도 거리:

${\displaystyle d_{L}(z)=(1+z)d_{M}(z)}$

다시 말하지만, 이 공식은 태양계도 물체도 그들 사이의 선에 평행한 독특한 속도 성분을 가지고 있지 않다면 엄격히 정확하다. 그렇지 않으면, 이 경우에 해당되는 적색 편향은 ${\displaystyle d_{}}$ $M{\displaystyle {}_{}}$, ${\displaystyle d_{M}}$에 사용해야 하지만$$ 인자$({\displaystyle 1}$+ ${\displaystyle z}$) ${\displaystyle(1+z)$는 측정된 적색 편향수를 사용해야 하며$$$,{\displaystyle \sqrt{}}$ (${\displaystyle \sqrt{1}}$ +${\displaystyle \sqrt{v}}$ / ${\displaystyle \sqrt{c}}$)${\displaystyle }$/${\displaystyle \sqrt{}}$( ${\displaystyle \sqrt{1}}$- ${\displaystyle \sqrt{v}}$/${\displaystyle \sqrt{}}$)를 곱하여 개체의 고유 속도에 대해 또 다른 보정을 해야 한다.${\displaystyle {\sqrt$ {($1+v/c)/(1-v/c)}},$ 여기서$$ v는 우리로부터 멀리 떨어진 물체의 고유 속도의 구성 요소다. 이렇게 하면, 광도 거리는 각 직경 거리에${\displaystyle }$(${\displaystyle 1}$+ z${\displaystyle {}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$,${\디스플레이$ 스타일 $(1+z)^{2$}를 곱한 것과 같을 것이다. 여기서$$ z는 에테르링턴의 상호주의 정리(아래 참조)에 따라 측정된 적색 편향이다.

• 경량 이동 거리:

${\displaystyle d_{T}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{{(1+z')E(z')}}}}}}}$

There is a closed-form solution of this if ${\displaystyle \Omega _{r}=\Omega _{m}=0}$ involving the inverse hyperbolic functions ${\displaystyle {\text{arcosh}}}$ or ${\displaystyle {\text{arsinh}}}$ (or involving inverse trigonometric functions if the cosmological constant has the other sign). $\Omega {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle r_{}}$= ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {\Omega \mathrm{}}_{}}$= ${\displaystyle 0}$ ${\displaystyle \Oomega _{r}=\Oomega$ $_{\$$Lambda }=0}$일 경우, $d$(z)에는 닫힌 형태 솔루션이 있지만, $z{\displaystyle (d_{}}$에는 없다${\displaystyle .}$ ${\style$ z($d_{T}).$$}$

두 거리 측정값이 평탄한 우주에서 ${\displaystyle \mathrm{등가}}$하도록 제한 ${\displaystyle {\Omega }_{}}$ k${\displaystyle {}_{}}$→ 0 ${\displaystyle \Oomega _{k}\to$ 0$\}$을 취함으로써 편차 거리는 횡단 편차 거리로부터 회복된다는 점에 유의한다.

Age of the universe is ${\displaystyle \lim _{z\to \infty }d_{T}(z)/c}$, and the time elapsed since redshift ${\displaystyle z}$ until now is: ${\displaystyle t(z)=d_{T}(z)/c.$$}$

대체 용어

피블스(1993)는 가로 방향 콤보빙 거리를 "사각형 크기 거리"라고 부르는데, 이는 각 직경 거리로 오인해서는 안 된다.^[1] 때때로 기호 $\chi {\displaystyle }$ ${\displaystyle \chi }$ 또는$$ $r{\displaystyle }$ ${\displaystyle r}$이(가) 콤보빙 및 각도 직경 거리를 모두 나타내기 위해 사용된다$$. 때때로, 가벼운 여행 거리는 "돌아보기 거리"라고도 불린다.

세부 사항

코모빙 거리

기본적인 관찰자, 즉 둘 다 허블 흐름을 따라 움직이고 있는 관찰자 사이의$$ 접근 거리 ${\displaystyle d_{}}$ C ${\$는 시간에 따라 변하지 않는데, 이는 우주가 팽창하는 것을 설명하기 때문이다. 접근 거리는 가시선(LOS)을 따라 주변의 기본 관찰자의 적절한 거리를 통합하여 얻지만, 적절한 거리는 일정한 우주 시간에서의 측정치가 산출하는 값이다.

표준 우주론에서, 우주론자들이 물체들 사이의 거리를 측정하기 위해 사용하는 두 개의 밀접하게 관련된 거리 측정값이다; 우주론자들은 현재 적절한 거리 측정값이다.

공전 거리(우리 자신의 움직임에 대해 작은 보정으로)는 시차로부터 얻을 수 있는 거리로, 도 단위의 시차(parallax)는 현재 태양을 통과하여 먼 물체를 중심으로 하는 원의 원주에 대한 천문 단위의 비율과 같기 때문에 360°를 곱한 것이다. 그러나 메가파섹을 넘는 물체는 시차(가이아 우주망원경은 7마이크로카초의 정밀도로 가장 밝은 별들의 시차(paralax)를 측정한다)가 너무 작아서 우리 로컬 그룹 밖의 은하의 시차(paralax)는 측정할 수 없다.

적정거리

적절한 거리는 우주의 팽창으로 인해 시간이 지남에 따라 변할 수 있는 우주적 시간의 특정 순간에 먼 물체가 있는 곳에 대략 해당한다. 우주의 팽창에 따른 거리(군집 내 은하계의 움직임과 같은 다른 국소적 요인)로 인해 시간적으로 변하지 않는 거리를 주는 우주 팽창에 따른 거리 요소, 즉 우주 팽창 거리는 현재 적절한 거리다.

횡방향 합선 거리

Two comoving objects at constant redshift ${\displaystyle z}$ that are separated by an angle ${\displaystyle \delta \theta }$ on the sky are said to have the distance ${\displaystyle \delta \theta d_{M}(z)}$, where the transverse comoving distance ${\displaystyle d_{M}}$ is defined appropriate리의

각도 지름 거리

An object of size ${\displaystyle x}$ at redshift ${\displaystyle z}$ that appears to have angular size ${\displaystyle \delta \theta }$ has the angular diameter distance of ${\displaystyle d_{A}(z)=x/\delta \theta }$. This is commonly used to observe so called standard rulers, for example ibaryon 음향 진동의 맥락.

조도 거리

If the intrinsic luminosity ${\displaystyle L}$ of a distant object is known, we can calculate its luminosity distance by measuring the flux ${\displaystyle S}$ and determine ${\displaystyle d_{L}(z)={\sqrt {L/4\pi S}}}$, which turns out to be equivalent to the expression above for ${\displaystyle d_L(}$${\displaystyle z}$) ${\displaystyle d_{L}(z$ 이 양은 우주 팽창의 가속도를 발견하기 위해 처음 사용된 Ia 초신성형 같은 표준초들의 측정에 중요하다.

경량 이동 거리

${\displaystyle {이}_{}}$ $거리{\displaystyle {}_{}}$ d T ${\$$T}}}$은 물체로부터 관찰자에게 빛의 속도에 곱한 빛이 도달하는 데 걸린 시간(년)이다$$. 예를 들어, 이 거리 측정에서 관측 가능한 우주의 반지름은 우주의 나이에 빛의 속도(1광년/년)를 곱한 시대가 된다. 즉, 138억 광년이다.

에테르링턴의 거리 이중성

Etherington의 거리-이중성 방정식은 표준 초의 광도 거리와 각도 지름 거리 사이의 관계다. d ${\displaystyle L_{}}$=${\displaystyle }$( ${\displaystyle 1}$+ z${\displaystyle {}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}{}_{}}$ ${\displaystyle A_{}}$ ${\$d}}}로 표현된다.$A}$

참고 항목

• 빅뱅
• 코모빙 거리
• 프리드만 방정식
• 파르세크
• 물리 우주론
• 우주 거리 사다리
• 프리드만-레마슈트레-로베르톤-워커 미터법
• 아원자 척도

참조

• 스콧 도델슨, 모던 코스모ology. 학술신문(2003년).

외부 링크

• '우주의 거리 척도'는 서로 다른 우주적 거리 측도를 비교한다.
• '우주론에서의 거리 측도'는 다양한 거리 측도를 세계 모델과 적색 변형의 함수로 계산하는 방법을 자세히 설명한다.
• iCosmos: Cosmology Calculator (Graph Generation 포함)는 서로 다른 거리 측정값을 우주 모델과 적색 편향의 함수로 계산하고 적색 편향 0에서 20까지의 모델에 대한 그림을 생성한다.