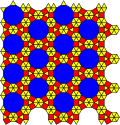
데미레겔러 타일링

Demiregular tiling

기하학에서 제습 기울기는 2개 이상의 정규 다각형 면으로 만든 유클리드 테셀레이션의 집합이다.다른 작가들은 다른 일련의 기울기를 열거했다.대칭 궤도를 살펴보는 보다 체계적인 접근방식은 20개가 있는 2-통일 기울기이다.제습형 틸팅 중 일부는 실제로 3-통일형 틸팅이다.

2인치 기울기 20개

그룬바움(Grünbaum)과 셰퍼드(Shephard)는 틸링스(Tilings)와 패터런스(Patterns)에 있는 20개의 2-제복 기울기 전체 목록을 열거했다. 1987:

2-10 틸팅
cmm, 2*22
2-uniform n4.svg
(44; 33.42)1 		cmm, 2*22
2-uniform n3.svg
(44; 33.42)2 		pmm, *2222
2-uniform n14.svg
(36; 33.42)1 		cmm, 2*22
2-uniform n15.svg
(36; 33.42)2 		cmm, 2*22
2-uniform n6.svg
(3.42.6; (3.6)2)2 		pmm, *2222
2-uniform n7.svg
(3.42.6; (3.6)2)1 		pmm, *2222
2-uniform n11.svg
((3.6)2; 32.62)
p4m, *442
2-uniform n2.svg
(3.12.12; 3.4.3.12)		 p4g, 4*2
2-uniform n16.svg
(33.42; 32.4.3.4)1 		2배의
2-uniform n17.svg
(33.42; 32.4.3.4)2 		p6m, *632
2-uniform n10.svg
(36; 32.62)		 p6m, *632
2-uniform n19.svg
(36; 34.6)1 		p6,632
2-uniform n20.svg
(36; 34.6)2 		cmm, 2*22
2-uniform n12.svg
(32.62; 34.6)
p6m, *632
2-uniform n18.svg
(36; 32.4.3.4)		 p6m, *632
2-uniform n9.svg
(3.4.6.4; 32.4.3.4)		 p6m, *632
2-uniform n8.svg
(3.4.6.4; 33.42)		 p6m, *632
2-uniform n5.svg
(3.4.6.4; 3.42.6)		 p6m, *632
2-uniform n1.svg
(4.6.12; 3.4.6.4)		 p6m, *632
2-uniform n13.svg
(36; 32.4.12)

기카의 목록(1946)

기카는 그 중 10개의 꼭지점 유형을 2개 또는 3개의 꼭지점 유형으로 나열하여 반정형 다형 파티션이라고 부른다.[1]

2-uniform n1.svg 2-uniform n8.svg 2-uniform n9.svg
플레이트 XXVII
12번
4.6.12
3.4.6.4		 13번
3.4.6.4
3.3.3.4.4		 13번 비스.
3.4.4.6
3.3.4.3.4		 13번 테르.
3.4.4.6
3.3.3.4.4		 플레이트 XXIV
13번 쿼터.
3.4.6.4
3.3.4.3.4
2-uniform n13.svg 3-uniform 48.svg
14번
33.42
36 		플레이트 XXVI
14번 비스.
3.3.4.3.4
3.3.3.4.4
36 		14번 테르.
33.42
36 		15번
3.3.4.12
36 		플레이트 XXV
16번
3.3.4.12
3.3.4.3.4
36

스타인하우스의 명단 (1969년)

스타인하우스는 11개의 정규 및 반정형 폴리곤을 넘어 일반 폴리곤의 비균형 테셀레이션 5가지 예를 제시한다.[2] (모두 정점 2종류가 있는데 반해 정점 1종은 3종류다.)

2시 30분 3시 30분
2-uniform n8.svg 2-uniform n9.svg 2-uniform n13.svg 2-uniform n16.svg 3-uniform 9.svg
이미지 85
33.42
3.4.6.4		 이미지 86
32.4.3.4
3.4.6.4		 이미지 87
3.3.4.12
36 		이미지 89
33.42
32.4.3.4		 이미지 88
3.12.12
3.3.4.12

크리츠로우 리스트 (1970년)

크라이트로우는 데미 정규 테셀레이션 14개를 식별하며, 7개는 2-통일, 7개는 3-통일이다.

그는 얼굴 순서를 구별하기 위해 위첨자로 정점 유형의 문자 이름을 코드화한다.그는 A, B, C, D, F, J가 전체 비행기의 연속 커버의 일부가 될 수 없음을 인식한다.

A
(iii)		 B
(iii)		 C
(iii)		 D
(iii)		 E
(iii)		 F
(iii)		 G
(iii)		 H
(iii)		 J
(iii)		 K(2)
(지역)
Regular polygons meeting at vertex 3 3 7 42.svg
3.7.42		 Regular polygons meeting at vertex 3 3 8 24.svg
3.8.24		 Regular polygons meeting at vertex 3 3 9 18.svg
3.9.18		 Regular polygons meeting at vertex 3 3 10 15.svg
3.10.15		 Regular polygons meeting at vertex 3 3 12 12.svg
3.12.12 		Regular polygons meeting at vertex 3 4 5 20.svg
4.5.20		 Regular polygons meeting at vertex 3 4 6 12.svg
4.6.12 		Regular polygons meeting at vertex 3 4 8 8.svg
4.8.8 		Regular polygons meeting at vertex 3 5 5 10.svg
5.5.10		 Regular polygons meeting at vertex 3 6 6 6.svg
63
L1
(데미)		 L2
(데미)		 M1
(데미)		 M2
(iii)		 N1
(데미)		 N2
(iii)		 P(3)
(지역)		 Q1
(iii)		 Q2
(iii)		 R
(iii)		 S(1)
(지역)
Regular polygons meeting at vertex 4 3 3 4 12.svg
3.3.4.12		 Regular polygons meeting at vertex 4 3 4 3 12.svg
3.4.3.12		 Regular polygons meeting at vertex 4 3 3 6 6.svg
3.3.6.6		 Regular polygons meeting at vertex 4 3 6 3 6.svg
3.6.3.6 		Regular polygons meeting at vertex 4 3 4 4 6.svg
3.4.4.6		 Regular polygons meeting at vertex 4 3 4 6 4.svg
3.4.6.4 		Regular polygons meeting at vertex 4 4 4 4 4.svg
44 		Regular polygons meeting at vertex 5 3 3 4 3 4.svg
3.3.4.3.4 		Regular polygons meeting at vertex 5 3 3 3 4 4.svg
3.3.3.4.4 		Regular polygons meeting at vertex 5 3 3 3 3 6.svg
3.3.3.3.6 		Regular polygons meeting at vertex 6 3 3 3 3 3 3.svg
36
2시 30분
1 2 4 6 7 10 14
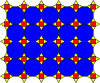2-uniform n2.svg
(3.12.12; 3.4.3.12)		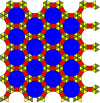 2-uniform n13.svg
(36; 32.4.12)		 2-uniform n1.svg
(4.6.12; 3.4.6.4)		 2-uniform n11.svg
((3.6)2; 32.62)		 2-uniform n9.svg
(3.4.6.4; 32.4.3.4)		 2-uniform n18.svg
(36; 32.4.3.4)		 2-uniform n5.svg
(3.4.6.4; 3.42.6)
E+L2 L1+(1) N1+G M1+M2 N2+Q1 Q1+(1) N1+Q2
3시 30분
3 5 8 9 11 12 13
(3.3.4.3.4; 3.3.4.12, 3.4.3.12) (36; 3.3.4.12; 3.3.4.3.4) (3.3.4.3.4; 3.3.3.4.4, 4.3.4.6) (36, 3.3.4.3.4) (36; 3.3.4.3.4, 3.3.3.4.4) (36; 3.3.4.3.4; 3.3.3.4.4) (3.4.6.4; 3.42.6)
L1+L2+Q1 L1+Q1+(1) N1+Q1+Q2 Q1+(1) Q1+Q2+(1) Q1+Q2+(1) N1+N2
클레임 틸링 및 듀얼
Demi 1 Uniform.svg Demi 2 Uniform.svg Demi 3 Uniform.svg Demi 4 Uniform.svg Demi 5 Uniform.svg Demi 6 Uniform.svg Demi 7 Uniform.svg
Demi 1 Dual.svg Demi 2 Dual.svg Demi 3 Dual.svg Demi 4 Dual.svg Demi 5 Dual.svg Demi 6 Dual.svg Demi 7 Dual.svg

참조

  1. ^ 기카(1946) 페이지 73-80
  2. ^ 1969년, 페이지 79-82
  • 기카, M.예술과 삶의 기하학, (1946), 제2판, 뉴욕: 도버, 1977.
  • Keith Critchlow, Order in Space: 디자인 소스 북, 1970, 페이지 62–67
  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. 페이지 35-43
  • Steinhaus, H. Matheical Snapshots 3번째 에드, (1969), 옥스퍼드 대학 출판부, (1999) 뉴욕: 도버
  • Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman. ISBN 0-7167-1193-1. 페이지 65
  • Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
  • 데미레굴러 틸링 찾기, 헬머 아스락센

외부 링크