외부 탄도학
External ballistics외부 탄도학 또는 외부 탄도학은 비행 중인 발사체의 행동을 다루는 탄도학의 한 부분입니다.발사체는 동력 또는 무동력, 유도 또는 무유도, 스핀 또는 지느러미 안정화, 대기 또는 우주의 진공 상태에서 비행할 수 있지만,[1] 가장 확실한 것은 중력장의 영향을 받아 비행합니다.
총으로 발사된 발사체는 동력이 없을 수 있으며, 발사체가 [2]총신을 벗어날 때까지 추진체의 점화로부터 모든 속도를 유도합니다.그러나, 외부 탄도 분석은 또한 로켓포 보조 발사체 및 총 발사 로켓의 궤적을 다루며, 로켓 모터 또는 공기 호흡 엔진과 같은 탑재 추진 시스템의 내부 탄도로부터 모든 궤적 속도를 획득하는 로켓,활성화 단계 및 모터 소진 후 둘 다.외부 탄도학은 또한 공, 화살 등과 같은 다른 발사체의 자유 비행과 관련이 있습니다.
발사체에 작용하는 힘
비행 중 발사체에 작용하는 주요 또는 주요 힘은 중력, 항력 및 존재하는 경우 바람, 동력 비행 중인 경우 추력, 유도된 경우 제어 표면에 의해 전달되는 힘입니다.
소형 무기 외부 탄도 응용 분야에서는 중력이 발사체에 아래쪽으로 가속을 가해 발사체가 시선에서 떨어지도록 합니다.드래그 또는 공기 저항은 속도의 제곱에 비례하는 힘으로 발사체를 감속시킵니다.바람이 발사체를 궤도에서 벗어나게 합니다.비행 중 중력, 항력 및 바람은 발사체의 경로에 큰 영향을 미치며, 발사체가 어떻게 이동할지 예측할 때 고려해야 합니다.
중간에서 긴 범위 및 비행 시간의 경우, 중력, 공기 저항 및 바람 외에도 외부 요인 단락에 설명된 몇 가지 중간 또는 중간 변수가 소형 무기를 고려해야 합니다.메소 변수는 각도가 있는 사격 시나리오나 확장된 사격 범위를 처리해야 하는 총기 사용자에게 중요할 수 있지만, 일반적인 사냥 및 표적 사격 거리에서는 거의 관련이 없습니다.
장기에서 매우 긴 소형 무기 목표 범위 및 비행 시간에 대해서는 장거리 요인 단락에 설명된 것과 같은 사소한 영향과 힘이 중요해지고 고려되어야 합니다.이러한 작은 변수의 실질적인 효과는 단거리 및 중간 범위의 정상적인 그룹 산란이 이러한 효과가 발사체 궤적에 미치는 영향에 우선하기 때문에 대부분의 총기 사용자에게는 일반적으로 관련이 없습니다.
극도로 긴 사거리에서, 포병은 거의 직선이 아닌 궤도를 따라 발사해야 합니다. 공기 저항이 영향을 미치지만 포물선에 더 가깝습니다.극단적인 장거리 발사체는 상황에 따라 라인에서 목표물을 향해 상당한 편향이 발생하며, 조준할 때 모든 외부 요인과 장거리 요인을 고려해야 합니다.파리 건과 같은 매우 큰 구경의 포병의 경우, 이 기사에서 다루지 않은 매우 미묘한 효과는 조준 솔루션을 더욱 개선할 수 있습니다.
탄도 미사일의 경우, 관련된 고도도 상당한 영향을 미치는데, 비행의 일부는 회전하는 지구보다 훨씬 높은 진공 상태에서 발생하여 발사 시 목표물을 꾸준히 이동시킵니다.
비행 중 비구면 발사체 안정화
비행 중 비구면 발사체를 안정화하기 위해 두 가지 방법을 사용할 수 있습니다.
- M829 Armor-Piercing, Fin-Stabilized, Discarding Savot(APFSDS)과 같은 화살이나 사봇과 같은 발사체는 꼬리 표면으로 압력 중심(CP)을 질량 중심(CM) 뒤로 밀어넣어 안정성을 확보합니다.CM 조건 뒤의 CP는 안정적인 발사체 비행을 제공하며, 이는 공기역학적 힘으로 인해 발사체가 대기를 통해 비행하는 동안 뒤집히지 않는다는 것을 의미합니다.
- 소형 무기 탄환 및 포탄과 같은 발사체는 CP가 CM 앞에 있는 것을 처리해야 하며, 이는 비행 중에 이러한 발사체를 불안정하게 만듭니다.이러한 발사체를 안정화하기 위해 발사체는 종방향(후행으로 이어지는) 축을 중심으로 회전합니다.회전하는 질량은 CM 앞에 있는 CP의 불안정한 전복 토크에 대해 총알의 길이 축을 저항력으로 유지하는 자이로스코프 힘을 생성합니다.
외부 탄도학의 주효과
발사체/탄환 낙하 및 발사체 경로
비행 중인 발사체에 대한 중력의 영향을 종종 발사체 낙하 또는 총알 낙하라고 합니다.총의 조준 구성 요소를 제로로 만들 때 중력의 효과를 이해하는 것이 중요합니다.발사체 낙하를 계획하고 적절히 보상하기 위해서는 포물선 모양의 궤적을 이해해야 합니다.
발사체/탄환 낙하
발사체가 멀리 떨어진 목표물에 충격을 주려면 배럴이 목표물에 대해 양의 표고 각도로 기울어져 있어야 합니다.이는 발사체가 보어의 기계적 제약으로부터 자유로워지는 순간 중력의 영향에 반응하기 시작하기 때문입니다.보어의 중심축을 따라 내려가 무한대로 나가는 가상의 선을 출발선이라고 하며 발사체가 배럴을 떠나는 선이 됩니다.중력의 영향으로 인해 발사체는 절대로 출발선보다 높은 목표물에 충돌할 수 없습니다.양의 기울기를 가진 발사체가 아래로 이동할 때, 그것은 중력에 의해 초기 경로에서 빗나가면서 출발선 아래로 호를 그립니다.발사체/탄환 낙하는 보어에서 출발선 아래에 있는 발사체의 수직 거리로 정의됩니다.출발선이 위쪽 또는 아래쪽으로 기울어져 있더라도, 발사체 낙하는 여전히 탄환과 궤도를 따라 어느 지점에서 출발선 사이의 거리로 정의됩니다.발사체 낙하는 발사체의 실제 궤적을 설명하지 않습니다.그러나 발사체 낙하에 대한 지식은 속도 및 항력 거동과 같은 변수의 영향을 비교하여 궤도의 모양에 대해 두 개의 다른 발사체를 직접 비교할 때 유용합니다.
발사체/탄환 경로
멀리 떨어진 표적을 타격하려면 사격자의 눈에서 출발선을 향해 아래쪽으로 조준 시스템의 중심선을 통해 시선을 각도로 조정하여 달성되는 적절한 양의 고도 각도가 필요합니다.이 작업은 단순히 조준기를 기계적으로 아래로 조정하거나, 전체 조준기를 아래로 경사지는 것으로 알려진 마운트에 고정하거나, 두 가지를 모두 조합하여 수행할 수 있습니다.이 절차는 목표물에 조준을 맞추기 위해 총신을 들어올려야 할 때 총구를 높이는 효과가 있습니다.특정 고도 각도에서 총부리를 남기는 발사체는 총부리 속도, 중력, 공기역학적 항력과 같은 다양한 요인에 따라 특성이 달라지는 탄도 궤적을 따릅니다.이 탄도 궤적을 총탄 경로라고 합니다.만약 발사체가 스핀 안정화된다면, 라이플링이 "우측 반전"을 사용한다면, 공기역학적 힘도 예측 가능하게 궤도를 약간 오른쪽으로 호를 그리게 될 것입니다.어떤 통들은 왼쪽으로 꼬아서 잘려나가고, 그 결과 총알은 왼쪽으로 호를 그리게 됩니다.따라서 이 경로 편차를 보정하려면 조준경도 각각 왼쪽 또는 오른쪽으로 조정해야 합니다.일정한 바람은 또한 예측 가능하게 총알 경로에 영향을 주어 바람 방향에 따라 약간의 좌우, 그리고 약간의 위아래로 밀어줍니다.이러한 편차의 크기는 회전하는 총알이 점질량 궤적에서 약간 벗어나 꾸준히 예측 가능하게 정렬되는 경향이 있는 "휴식의 요"라고 불리는 현상으로 인해 총알이 궤적의 위쪽 또는 아래쪽 경사에 있는지에 의해 영향을 받습니다.그럼에도 불구하고, 이러한 각 궤적 섭동은 세부적인 분석 모델링 및 테스트 범위 측정의 조합을 통해 발사체 공기역학 계수가 설정되면 예측할 수 있습니다.
발사체/탄환 경로 분석은 다양한 알려진 거리에서 사격을 위해 조준선에 수직 상승 및 수평 편향 보정이 얼마나 적용되어야 하는지를 예측하는 탄도 테이블을 설정할 수 있기 때문에 사격 선수에게 매우 유용합니다.가장 상세한 탄도표는 장거리 포병용으로 개발되었으며 고도, 범위 및 편향의 세 축 방향과 피치, 요 및 스핀의 세 회전 방향을 따르는 공기역학적 거동을 설명하는 6개의 자유도 궤적 분석을 기반으로 합니다.소형 무기 애플리케이션의 경우 궤적 모델링은 종종 이러한 자유도 중 4개만 포함하는 계산으로 단순화될 수 있으며, 피치, 요 및 스핀의 효과를 궤적 편향을 설명하기 위한 휴식의 요 효과로 묶습니다.세부적인 범위 표가 설정되면 사격 선수는 목표 범위, 바람, 기온 및 습도, 지형 고도 차이와 같은 기타 기하학적 고려 사항에 따라 비교적 빠르게 시야를 조정할 수 있습니다.
투영 경로 값은 조준기 높이 또는 보어 중심선 위의 조준기 거리와 조준기가 영점이 되는 범위에 의해 결정되며, 이는 차례로 표고 각도를 결정합니다.탄도 궤도를 따르는 발사체는 전진과 수직의 움직임을 모두 가지고 있습니다.공기 저항으로 인해 전진 운동이 느려지고, 점 질량 모델링에서 수직 운동은 표고 각도와 중력의 조합에 따라 달라집니다.처음에 발사체는 시선 또는 수평 조준면에 대해 상승합니다.발사체는 결국 수직 속도 성분이 중력의 영향으로 0으로 붕괴하는 정점(궤도 포물선의 가장 높은 지점)에 도달한 다음 하강하기 시작하여 결국 지구에 영향을 미칩니다.원하는 대상까지의 거리가 멀어질수록 표고 각도가 커지고 정점이 높아집니다.
발사체 경로는 수평 조준면을 두 번 교차합니다.총에 가장 가까운 지점은 총알이 시선을 통과하는 동안 발생하며 근점이라고 불립니다.두 번째 점은 발사체가 시선을 통해 하강할 때 발생합니다.그것은 far zero라고 불리며 총에 대한 거리의 현재 시야를 정의합니다.발사체 경로는 궤적을 따라 다양한 지점에서 수평 조준면 위 또는 아래의 거리로 수치적으로 설명됩니다.이는 고도 각도에 관계없이 출발선이 포함된 평면을 참조하는 발사체 낙하와는 대조적입니다.이 두 파라미터는 각각 다른 기준 데이텀을 사용하기 때문에,발사체가 출발선 아래에서 추적하고 있음에도 불구하고 수평 또는 수평에 가까운 수평 촬영의 경우 지표면뿐만 아니라 시선과 관련하여 실제적이고 상당한 높이를 얻을 수 있기 때문에 상당한 혼란이 발생할 수 있습니다.
최대 직사거리 및 전투 0
발사체 낙하 및 경로에 대한 지식은 발사체의 실제 궤적을 설명하지 않더라도 사격자에게 몇 가지 실용적인 용도가 있습니다.예를 들어, 특정 범위 도달에 대한 수직 발사체 위치가 사격자가 타격하고자 하는 표적 영역의 수직 높이 내에 있는 경우, 조준점은 반드시 해당 범위에 대해 조정될 필요는 없습니다. 발사체는 특정 [3]표적에 대해 충분히 평평한 점-공백 범위 궤적을 가지고 있는 것으로 간주됩니다."전투 제로"라고도 알려진, 최대 직사거리는 또한 군대에게 중요합니다.병사들은 이 범위 내의 모든 목표물을 향해 총을 쏘도록 지시받습니다. 단지 적의 목표물의 질량 중심에 무기의 조준을 배치하는 것만으로 말입니다.조준 사격이 잘 되면 적병의 몸통에 명중하기 때문에 거리 추정의 오류는 전술적으로 무관합니다.돌격소총에서 높은 조준경과 더 빠른 속도의 탄환에 대한 현재의 추세는 부분적으로 소총을 [4][5][6]더 쉽게 사용할 수 있도록 최대 직사거리를 확장하려는 욕구 때문입니다.
드래그 저항
컴퓨터 유체 역학과 같은 수학적 모델은 드래그 또는 공기 저항의 효과를 계산하는 데 사용됩니다. 그것들은 상당히 복잡하고 아직 완전히 신뢰할 수는 없지만, 연구는 진행 [7]중입니다.따라서 비행 궤적을 적절하게 설명하는 데 필요한 발사체 공기역학적 특성을 설정하는 가장 신뢰할 수 있는 방법은 경험적 측정입니다.
표준 모양의 발사체에 대해 생성된 고정 드래그 곡선 모델
Mayevski/Siacci 방법 및 1881년에 도입된 G1 드래그 모델에 기반한 탄도 테이블 또는 탄도 소프트웨어의 사용은 외부 탄도 작업에 사용되는 가장 일반적인 방법입니다.발사체는 탄환 모양의 공기 저항(끌림 계수)과 그 단면 밀도(질량과 탄환 직경의 함수)를 결합한 탄도 계수 또는 BC로 설명됩니다.
질량 m, 속도 v, 직경 d를 가진 발사체가 경험하는 항력으로 인한 감속은 1/BC, 1/m, v², d²에 비례합니다.BC는 표준 G1 발사체와 비교한 탄도 효율의 비율을 제공합니다. G1 발사체는 평평한 바닥, 3.28 칼리버/직경의 길이, 점에 대한 2 칼리버/직경 접선 곡선을 가진 가상 발사체입니다.G1 표준 발사체는 1881년 독일의 철강, 탄약 및 군수품 제조업체인 크루프에 의해 정의된 "C" 표준 기준 발사체에서 유래되었습니다.G1 모델 표준 발사체의 BC는 [8]1입니다.프랑스 게브르 위원회는 이 발사체를 첫 번째 기준 발사체로 사용하기로 결정하고 G1이라는 [9][10]이름을 붙였습니다.
0.177~0.50인치(4.50~12.7mm) 범위의 스포츠 탄환은 G1 BC가 0.12~1.00 범위에 있으며 공기역학적으로 1.00이 가장 많고 0.12가 가장 작습니다.BC의 § 1.10의 매우 낮은 항력 탄환은 모노 메탈 로드로 CNC 정밀 선반에서 설계 및 생산될 수 있지만, 종종 특수 [11]배럴이 장착된 맞춤형 풀 보어 라이플에서 발사되어야 합니다.
단면 밀도는 발사체 또는 탄환의 매우 중요한 측면이며, 탄환과 같은 둥근 발사체의 경우 탄환 질량에 대한 정면 표면적(탄환 직경의 절반 제곱, 시간 파이)의 비율입니다.주어진 탄환 모양의 경우 정면 표면은 눈금의 제곱에 따라 증가하고 질량은 지름의 입방체에 따라 증가하기 때문에 단면 밀도는 보어 직경에 따라 선형으로 증가합니다.BC는 형상과 단면 밀도를 결합하기 때문에 G1 발사체의 반 스케일 모델은 BC 0.5, 4분의 1 스케일 모델은 BC 0.25입니다.
서로 다른 발사체 모양은 속도의 변화(특히 초음속과 아음속 사이)에 다르게 반응하기 때문에, 총알 제조업체가 제공하는 BC는 총알의 공통 속도 범위를 나타내는 평균 BC가 될 것입니다.소총 탄환의 경우 이것은 아마도 초음속일 것이고, 권총 탄환의 경우 아마도 아음속일 것입니다.초음속, 초음속 및 아음속 비행 시스템을 통과하는 발사체의 경우 BC는 단일 상수에 의해 잘 근사되지 않지만 마하 수 M의 함수 BC(M)로 간주됩니다. 여기서 M은 발사체 속도를 음속으로 나눈 값입니다.발사체를 비행하는 동안 M은 감소하므로 (대부분의 경우) BC도 감소합니다.
대부분의 탄도 테이블 또는 소프트웨어는 하나의 특정 항력 함수가 탄도 계수와 관련된 탄환의 항력 및 비행 특성을 정확하게 설명한다고 당연하게 생각합니다.이러한 모델은 워커터, 플랫 기반, 스피처, 보트 테일, 매우 낮은 드래그 등의 총알 유형 또는 모양을 구별하지 않습니다.그들은 게시된 BC에 표시된 대로 하나의 불변 항력 함수를 가정합니다.
그러나 여러 표준 투영 형상에 최적화된 여러 드래그 곡선 모형을 사용할 수 있습니다.여러 표준 투영 형상 또는 유형에 대한 고정 드래그 곡선 모델을 다음과 같이 부릅니다.
- G1 또는 Ingalls(2구경(블런트) 노즈오기브의 플랫 베이스 - 지금까지 가장 인기 있음)
- G2(애버딘 J 발사체)
- G5(짧은 7.5° 보트-테일, 6.19 캘리버 긴 접선)
- G6(플랫베이스, 6개 칼리버 긴 샹토기브)
- G7(길이 7.5°의 보트 테일, 10개의 캘리버 탄젠토기브, 매우 낮은 항력 탄환을 위해[12] 일부 제조업체에서 선호함)
- G8 (플랫베이스, 길이 10 칼리브르 샹토기브)
- GL(블런트 리드 노즈)
다양한 속도 체제가 .338 칼리브레 소총 탄환에 미치는 영향은 도플러 레이더가 G1 BC [13][14]데이터를 확립했다고 명시한 .338 Lapua Magnum 제품 브로셔에서 확인할 수 있습니다.이 브로셔와 같은 데이터를 게시하는 이유는 Siacci/Mayevski G1 모델이 사용된 기준 발사체 모양에서 상당히 벗어난 특정 발사체의 항력 거동에 맞게 조정될 수 없기 때문입니다.Siacci/Mayevski G1 모델에 기반을 둔 일부 탄도 소프트웨어 설계자는 사용자에게 서로 다른 속도 시스템에 대해 몇 가지 다른 G1 BC 상수를 입력하여 BC 상수 하나만 사용하는 계산에 비해 더 긴 범위에서 탄환 비행 동작과 더 가깝게 일치하는 탄도 예측을 계산할 수 있는 가능성을 제공합니다.
위의 예는 고정 드래그 곡선 모델의 중심 문제를 보여줍니다.이러한 모형은 관심 있는 발사체가 기준 발사체와 동일한 모양이거나 기준 발사체와 매우 유사한 모양을 갖는 한 만족스러운 정확한 예측을 산출할 수 있습니다.기준 발사체 모양에서 벗어나면 [15][16]예측의 정확도가 떨어집니다.적용된 기준 발사체에서 발사체가 벗어나는 정도는 폼 팩터(i)[17]로 수학적으로 표현됩니다.폼 팩터는 관심 발사체가 경험하는 항력과 주어진 속도(범위)에서 사용되는 기준 발사체가 경험하는 항력을 비교하는 데 사용할 수 있습니다.발사체의 실제 항력 곡선이 사용된 기준 발사체의 고정 항력 곡선에서 크게 벗어날 수 있다는 문제는 전통적인 항력 모델링 접근 방식을 체계적으로 제한합니다.그러나 비교적 단순하기 때문에 일반적인 사격 대중에게 설명하고 이해할 수 있으므로 탄도 소프트웨어 예측 개발자와 제품을 판매하려는 총알 제조업체 사이에서도 인기가 있습니다.
고급 드래그 모델
페자 모형
탄도 계산기를 만드는 또 다른 시도는 1980년에 Dr.에 의해 제시된 모델입니다.아서 J. 페이사.[18]Pejsa 박사는 그의 웹사이트에서 그의 방법이 [19]이론적으로 2.5mm(0.1인치) 내에서 소총 탄환 궤적을 예측하고 0.3m/s(1ft/s) 내에서 914m(1,000yd)까지 총알 속도를 일관되게 예측할 수 있었다고 주장합니다.Pejsa 모델은 폐쇄형 솔루션입니다.
Pejsa 모델은 단 두 가지 속도 측정, 해당 속도 측정 사이의 거리 및 기울기 또는 감속 상수 [20]계수를 사용하여 주어진 비행 영역(예: 초음속 비행 영역) 내의 발사체를 예측할 수 있습니다.모형을 사용하면 드래그 곡선이 세 개의 다른 [21]점에서 기울기(참/보정) 또는 곡률을 변경할 수 있습니다.하향 속도 측정 데이터를 주요 변곡점 주변에 제공하여 마하 대 CD 표와 매우 유사한 발사체 지연 속도를 보다 정확하게 계산할 수 있습니다.Pejsa 모델을 사용하면 다양한 총알 모양과 크기의 지연율에서 미묘한 차이를 고려하여 기울기 계수를 조정할 수 있습니다.0.1(평코 탄환)에서 0.9(매우 낮은 항력 탄환) 사이의 범위입니다.이 기울기 또는 감속 상수 인자를 알 수 없는 경우 기본값 0.5가 사용됩니다.시험 발사 측정의 도움을 받아 특정 탄환/소총 시스템/사격기 조합에 대한 기울기 상수를 결정할 수 있습니다.이러한 시험 발사는 60%에서 수행하는 것이 바람직하며, 극단적인 장거리 탄도 예측의 경우 불규칙한 천음속 효과를 멀리하면서 관심 발사체의 초음속 범위의 80%에서 90%까지 수행해야 합니다.이를 통해 Pejsa 모델을 쉽게 조정할 수 있습니다.Pejsa 모델의 실질적인 단점은 이러한 더 나은 예측을 제공하기 위한 정확한 발사체 특정 하향 속도 측정이 대다수의 사격 애호가들에 의해 쉽게 수행될 수 없다는 것입니다.
속도 데이터 포인트가 알려져 있고 해당 속도 측정 사이의 거리가 알려진 경우 주어진 기울기 상수 인자에 대해 평균 지연 계수를 계산할 수 있습니다.분명히 이것은 같은 비행 체제 내에서만 사실입니다.속도의 경우 속도는 벡터의 양이고 속도는 속도 벡터의 크기이므로 실제 속도는 의미합니다.전력 함수에는 일정한 곡률이 없기 때문에 단순 코드 평균을 사용할 수 없습니다.Pejsa 모델은 0.25 범위에서 가중 평균 지연 계수를 사용합니다.속도가 가까울수록 가중됩니다.지연 계수는 피트 단위로 측정되는 반면, 범위는 야드 단위로 측정되므로 0.25 * 3.0 = 0.75이며, 일부 지역에서는 0.75가 아닌 0.8이 사용됩니다.0.8은 수동 계산기에 쉽게 입력할 수 있도록 반올림한 값입니다.Pejsa 모델은 단순한 코드 가중 평균을 사용하지 않기 때문에 두 속도 측정을 사용하여 두 속도 측정 지점 사이의 미드레인지에서 코드 평균 지연 계수를 찾아 단거리 정확도로 제한합니다.시작 지연 계수를 찾기 위해 Dr.Pejsa는 그의 두 책에서 두 개의 다른 방정식을 제공합니다.첫 번째는 전력 [22]함수와 관련이 있습니다.두 번째 방정식은 R/4에서 가중 평균을 찾는 데 사용된 방정식과 동일합니다. 여기서 N * (R/2)을 추가합니다. 여기서 R은 중간에서 코드 평균 지연 계수에 대한 피트 범위이고 N은 기울기 상수 [23]계수입니다.시작 지연 계수를 찾은 후 R/4에서 가중 평균을 찾기 위해 반대 절차를 사용합니다. 시작 지연 계수에서 N*(R/4)을 뺀 값입니다.즉, N은 코드 라인의 기울기로 사용됩니다.Pejsa 박사는 R/4에서의 가중 평균 지연 계수가 좋은 근사치임을 증명하기 위해 검정력 시리즈에서 자신의 낙하 공식을 확장했다고 말합니다.이 닥터를 위해.Pejsa는 자신의 결론에 도달하기 위해 자신의 드롭 공식의 파워 시리즈 확장을 다른 이름 없는 드롭 공식의 파워 확장과 비교했습니다.두 검정력 시리즈의 네 번째 항은 0.25 범위의 지연 계수가 Pejsa의 드롭 공식에 사용되었을 때 일치했습니다.네 번째 용어는 N을 사용한 첫 번째 용어이기도 합니다.박사에 따르면 N = 0.36에서 중요하지 않고 사라진 N과 관련된 상위 항.Pejsa는 특히 N의 약 0.36에 대해 매우 정확한 선형 근사치를 만드는 행운의 우연이었습니다.지연 계수 함수를 사용하면 미적분에서 적분 가능 [24]함수의 평균을 찾는 것은 사소한 일이기 때문에 N에 대한 정확한 평균 값을 얻을 수 있습니다.페이사 박사는 지연 계수를 C * V로N 모델링할 수 있다고 말합니다. 여기서 C는 하강 공식과 N 기울기 [25]상수 계수를 도출하는 동안 사라지는 적합 계수입니다.
지연 계수는 속도 제곱을 지연 속도 A로 나눈 값과 같습니다.평균 지연 계수를 사용하면 Pejsa 모델이 주어진 비행 체제 내에서 폐쇄형 표현이 될 수 있습니다.
속도 데이터가 아닌 G1 탄도 계수를 사용할 수 있도록 하기 위해 Dr.Pejsa는 두 개의 기준 드래그 곡선을 제공했습니다.첫 번째 기준 드래그 곡선은 순수하게 시아치/마예프스키 지연 속도 함수를 기반으로 합니다.두 번째 기준 항력 곡선은 초음속 비행 체제에서 기울기 또는 감속 상수 계수가 0.5인 .30-06 스프링필드 카트리지, 볼, 칼리버 .30 M2 152 알갱이(9.8 g) 소총 스피처 총알을 사용하여 발사체 속도 2600 fps(792.5 m/s)에서 시아치/마예프스키 지연 속도 함수와 동일하게 조정됩니다.다른 비행 체제에서 두 번째 페자 기준 항력 곡선 모델은 0.0 또는 -4.0의 기울기 상수 인자를 사용합니다.이러한 감속 상수 인자는 Pejsa의 공식을 백업하여 확인할 수 있습니다(끌기 곡선 세그먼트는 V / C 형태에(2 - N) 적합하고 지연 계수 곡선 세그먼트는 V / (V(2 - N) / C) = C * VN 형태에2 적합합니다(여기서 C는 적합 계수입니다.주어진 마하 수치에서 지연 계수를 반환하는 그의 선택된 기준 드래그 곡선과 사전 정의된 수학 함수의 정확한 모양을 결정하는 데 사용된 경험적 테스트 데이터는 미군에 의해 카트리지, 볼, 칼리버.30 M2 탄환에 대해 제공되었습니다.지연 계수 함수의 계산에는 공기 밀도도 포함되는데, 페자는 이를 명시적으로 언급하지 않았습니다.Siacci/Mayevski G1 모델은 다음과 같은 감속 매개 변수화(60°F, 30 inHg 및 67% 습도, 공기 밀도 δ = 1.2209 kg/m3)[26]를 사용합니다.Pejsa 박사는 Siacci/Mayevski G1 드래그 곡선이 현대의 스피처 [27]총알에 잘 맞지 않기 때문에 두 번째 드래그 곡선을 사용할 것을 제안합니다.최적의 장거리 모델링을 위한 관련 지연 계수를 얻기 위해 Pejsa 박사는 특정 발사체에 대한 정확한 발사체 특정 하향 속도 측정 데이터를 사용하여 기준 드래그 곡선 파생 평균 지연 계수를 사용하는 대신 경험적으로 평균 지연 계수를 도출할 것을 제안했습니다.또한 그는 낮은 속도에서 실제 발사체 비행 거동을 경험적으로 테스트하기 위해 추진제 부하가 감소된 탄약을 사용할 것을 제안했습니다.감소된 추진제 부하로 작업할 때는 [21]화기에서 실험 부하를 발사할 때 발생할 수 있는 위험하거나 치명적인 조건(폭발)을 방지하기 위해 최대한 주의해야 합니다.
망게스 모형
Pejsa 모델만큼 잘 알려져 있지는 않지만, 추가적인 대체 탄도 모델은 1989년 5월 9일부터 11일까지 벨기에 브뤼셀의 브뤼셀 의회 센터에서 열린 미국 국방 준비 (ADPA) 11차 국제 탄도 심포지엄에서 Duff Manges 대령에 의해 발표되었습니다."직접 화기 시스템을 위한 폐쇄형 궤적 솔루션"이라는 제목의 논문은 의사록 1권, 추진 역학, 발사 역학, 비행 역학, 665-674페이지에 나와 있습니다.원래 120mm 탱크 총 탄약에 대한 발사체 항력을 모델링하기 위해 고안된 새로운 항력 계수 공식은 페자 모델에 대해 주장된 것과 유사한 결과를 가진 중앙 연소식 소총 탄약의 탄도 궤적에 후속적으로 적용되었습니다.
Manges 모델은 표준 G1 및 기타 유사성 곡선을 기반으로 "G" 곡선과 "탄도 계수"를 피하는 첫 번째 원칙 이론적 접근법을 사용합니다.이론적 설명은 크게 세 부분으로 나뉩니다.첫 번째는 궤도 미분 운동 방정식에 대한 닫힌 형태 솔루션을 허용하는 일련의 직교를 수학적으로 정의하여 점 질량 발사체의 평평한 궤적을 지배하는 2차원 미분 운동 방정식의 공식을 개발하고 해결하는 것입니다.실제 관측된 드래그 데이터로 빠르게 수렴하는 일련의 연속적인 근사 드래그 계수 함수가 생성됩니다.진공 궤적, 단순화된 공기역학, d'Antonio 및 오일러 항력 법칙 모델은 특별한 경우입니다.따라서 망즈 항력 법칙은 운동의 점질량 방정식에 대한 2차원 폐쇄형 솔루션을 얻는 데 사용된 초기 모델과 관련하여 통일된 영향을 제공합니다.이 논문의 세 번째 목적은 관찰된 실험 데이터에서 새로운 항력 함수를 얻기 위한 최소 제곱 적합 절차를 설명하는 것입니다.저자는 결과가 현대식 탱크 탄약에 대한 6개의 자유도 수치 계산 및 다양한 모양과 크기를 가진 중앙 연소식 소총 탄약에 대해 공개된 사격표와 매우 일치한다고 주장합니다.
마이크로소프트 Excel 응용 프로그램이 작성되어 풍동 획득 표 형식 드래그 계수의 최소 제곱 적합치를 사용합니다.또는 제조업체에서 제공한 탄도 궤적 데이터 또는 도플러 획득 속도 데이터를 적합시켜 모델을 보정할 수 있습니다.그런 다음 Excel 응용 프로그램은 사용자 지정 매크로 명령을 사용하여 관심 궤적 변수를 계산합니다.수정된 4차 룽게-쿠타 통합 알고리듬이 사용됩니다.Pejsa처럼, Colonel Manges는 중심 사격 소총의 정확도가 총알 위치의 경우 1인치의 10분의 1인치, 발사체 속도의 경우 초당 피트에 가깝다고 주장합니다.
제11회 국제 탄도 심포지엄의 의사록은 웨이백 머신의 2012-01-26 보관 웹사이트 http://www.ndia.org/Resources/Pages/Publication_Catalog.aspx 에서 국방 산업 협회(NDIA)를 통해 확인할 수 있습니다.
6 자유도 모형
PRODAS와 같은 고급 전문 탄도 모델도 사용할 수 있습니다.이 값은 6개의 자유도(6DoF) 계산을 기반으로 합니다.6 DoF 모델링은 발사체 피치, 요 및 롤 속도와 함께 공간에서의 x, y 및 z 위치를 설명합니다.6 DoF 모델링은 정교한 데이터 입력, 사용된 발사체에 대한 지식, 비전문 탄도학자에게는 [28]실용적이지 않지만 호기심 많고 컴퓨터에 능통하며 수학적 성향이 있는 사람에게는 불가능하지 않은 값비싼 데이터 수집 및 검증 방법을 필요로 합니다.다양한 발사체 모양에 대한 광범위한 테스트 범위 데이터를 줄이고, 치수 입력 지오메트리를 교정기로 정규화하며, 코 길이 및 반지름, 차체 길이 및 보트 꼬리 크기를 고려하고, 공기역학 계수의 전체 세트를 추정할 수 있는 반경험적 항공 예측 모델이 개발되었습니다.스핀 안정화 항공 예측 소프트웨어에 대한 초기 연구 결과 스피너 컴퓨터 프로그램이 탄생했습니다.[29]FINER 항공 예측 코드는 핀 안정화된 [30]발사체에 대한 6-d 입력을 계산합니다.안정성 분석에 필요한 질량, 무게 중심, 축 및 횡방향 관성 모멘트의 발사체 매개변수를 결정하는 고체 모델링 소프트웨어도 쉽게 사용할 수 있으며 컴퓨터 [31]프로그램에도 간단합니다.마지막으로, 4차 룽게-쿠타에 적합한 6-d의 수치 통합 알고리듬을 쉽게 사용할 [32]수 있습니다.아마추어 탄도학자가 탄환 너트 및 세차 운동과 함께 발사체 궤적의 자세한 분석 세부 사항을 조사하는 데 필요한 모든 것은 컴퓨터 프로그래밍 결정입니다.그럼에도 불구하고, 소형 무기 애호가들에게는 학문적 호기심을 떠나, 공개된 총알 탄도 계수를 기반으로 한 더 단순화된 점 질량 궤적에 비해 궤도를 6-d 정확도로 예측할 수 있는 것은 아마도 실질적인 의미가 없다는 것을 발견할 것입니다.6 DoF는 일반적으로 제한된 수의 (의도된) 군사 문제 발사체의 탄도 거동을 연구하는 항공우주 및 방위 산업과 군사 조직에서 사용됩니다.계산된 6개의 DoF 추세는 보다 일반적인 탄도 소프트웨어 애플리케이션에서 보정 테이블로 통합될 수 있습니다.
6 DoF 모델링 및 소프트웨어 애플리케이션은 수십 년 동안 전문적으로 잘 갖춰진 조직에서 사용되고 있지만, 일반적으로 계산 과정에서 (강화된) 개인 디지털 비서, 태블릿 컴퓨터 또는 스마트폰과 같은 모바일 컴퓨팅 장치의 컴퓨팅 성능 제한은 현장에서 즉시 수행되어야 합니다.2016년 스칸디나비아 탄약 제조업체 남모 라푸아 오이는 라푸아 탄도학이라는 이름의 6 DoF 계산 모델 기반 탄도 자유 소프트웨어를 출시했습니다.이 소프트웨어는 모바일 앱으로만 배포되며 Android 및 iOS [33]기기에서 사용할 수 있습니다.그러나 사용된 6DoF 모델은 6DoF 솔버에 총알 특정 드래그 계수(Cd)/도플러 레이더 데이터와 관심 있는 발사체의 기하학적 차원이 필요하기 때문에 라푸아 총알로 제한됩니다.다른 탄환의 경우, Lapua Ballistics 솔버는 G1 또는 G7 탄도 계수와 Mayevski/Siacci 방법으로 제한됩니다.
포병 소프트웨어 제품군
군사 조직은 NATO 군비 그룹(NAAG)의 SG2 Shareable(Fire Control) Software Suite(S4)와 같은 포병용 화기 제어 시스템을 위한 NABK(NATO Armension Ballistic Kernel)와 같은 탄도 모델을 개발했습니다.NATO 군비 탄도 커널은 4-DoF 수정 지점 질량 모델입니다.이것은 간단한 포인트 질량 모델과 계산 집약적인 6-DoF [34]모델 사이의 절충입니다.BALCO는 NATO 표준화 권고 4618에서 정의한 수학적 모델을 기반으로 한 궤도 시뮬레이션 프로그램으로, NATO 워킹그룹 내에서도 BALCO라는 6, 7 자유도 표준이 개발되었습니다.BALCO의 주요 목표는 제어 표면을 특징으로 하는 기존의 축 대칭 및 정밀 유도 발사체 모두에 대한 충실도가 높은 궤적을 계산하는 것입니다.BALCO 궤적 모델은 다음 기능을 구현하는 FORTRAN 2003 프로그램입니다.
- 6/7ºDoF 운동 방정식
- 7차 룽게, 쿠타, 펠베르크 통합
- 지구 모형
- 대기 모형
- 공기역학 모델
- 스러스트 및 베이스 번 모델
- 액추에이터[35] 모델
이러한 모델이 산출하는 예측은 비교 [36]연구의 대상이 됩니다.
도플러 레이더 측정
발사체에 대한 항력 또는 공기 저항 효과를 정확하게 설정하려면 도플러 레이더 측정이 필요합니다.Weibel 1000e 또는 Infinition BR-1001 도플러 레이더는 정부, 전문 탄도학자, 국방군 및 일부 탄약 제조업체에서 관심 있는 발사체의 비행 행동에 대한 실제 데이터를 얻기 위해 사용됩니다.정확하게 확립된 최첨단 도플러 레이더 측정은 3차원 공간에서 몇 밀리미터 이내의 정확도로 공기총 펠릿만큼 작은 발사체의 비행 행동을 결정할 수 있습니다.발사체 감속과 관련하여 수집된 데이터는 탄도 계수(BC) 또는 항력 계수(Cd)와 같은 여러 가지 방법으로 도출되고 표현될 수 있습니다.회전하는 발사체는 비행할 때 무게 중심에 대한 세차운동과 너트화를 모두 경험하기 때문에 6d 궤도 분석에 완전히 적용할 수 있도록 요 유도 항력 계수와 제로 요 항력 계수를 분리하기 위해 도플러 레이더 측정의 추가 데이터 감소가 필요합니다.
선반형 모노리식 솔리드 .50 BMG 초저 드래그 탄환(Lost River J40.510-773 그레인 모노리식 솔리드 탄환 / 트위스트 레이트 1:15 in)에 대한 도플러 레이더 측정 결과는 다음과 같습니다.
| 범위(m) | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 | 1800 | 1900 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 탄도 계수 | 1.040 | 1.051 | 1.057 | 1.063 | 1.064 | 1.067 | 1.068 | 1.068 | 1.068 | 1.066 | 1.064 | 1.060 | 1.056 | 1.050 | 1.042 | 1.032 |
BC 값의 초기 상승은 발사체의 항상 존재하는 요와 보어 밖으로의 세차운동에 기인합니다.테스트 결과는 한 번의 샷뿐만 아니라 여러 번의 샷에서 얻어졌습니다.총알의 제조사인 로스트 리버 탄도 기술은 총알의 BC 번호에 대해 1.062를 할당했습니다.
Lapua GB528 Scenar 19.44 g (300 g) 8.59 mm (0.338 in) 캘리브레이션 초저항력 탄환에 대한 도플러 레이더 측정 결과는 다음과 같습니다.
| 마하수 | 0.000 | 0.400 | 0.500 | 0.600 | 0.700 | 0.800 | 0.825 | 0.850 | 0.875 | 0.900 | 0.925 | 0.950 | 0.975 | 1.000 | 1.025 | 1.050 | 1.075 | 1.100 | 1.150 | 1.200 | 1.300 | 1.400 | 1.500 | 1.600 | 1.800 | 2.000 | 2.200 | 2.400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 드래그 계수 | 0.230 | 0.229 | 0.200 | 0.171 | 0.164 | 0.144 | 0.141 | 0.137 | 0.137 | 0.142 | 0.154 | 0.177 | 0.236 | 0.306 | 0.334 | 0.341 | 0.345 | 0.347 | 0.348 | 0.348 | 0.343 | 0.336 | 0.328 | 0.321 | 0.304 | 0.292 | 0.282 | 0.270 |
이 시험된 탄환은 마하 1.200 부근의 천음속 비행 체제에 진입할 때 최대 항력 계수를 경험합니다.
도플러 레이더 측정의 도움을 받아 탄환 속도가 음속 근처의 천음속 영역으로 느려지는 확장된 범위에서 사격할 때 가장 유용한 발사체 특정 항력 모델을 설정할 수 있습니다.여기서 수학적 모델링에 의해 예측된 발사체 항력이 발사체에 의해 경험되는 실제 항력에서 크게 벗어날 수 있습니다.추가적인 도플러 레이더 측정은 다양한 총알 [37]구조의 미묘한 기내 효과를 연구하는 데 사용됩니다.
정부, 전문 탄도학자, 국방군 및 탄약 제조업체는 대형 발사체에 장착된 원격 측정 프로브를 통해 수집된 측정값으로 도플러 레이더 측정값을 보완할 수 있습니다.
항력 또는 탄도 계수의 일반적 추세
일반적으로, 뾰족한 발사체는 둥근 코 탄환보다 항력 계수(Cd) 또는 탄도 계수(BC)가 더 좋을 것이고, 둥근 코 탄환은 평평한 코 탄환보다 더d 나은 C 또는 BC를 가질 것입니다.더 낮은 점 각도를 생성하는 큰 반지름 곡선은 특히 초음속에서 더 낮은 항력을 생성합니다.속이 빈 점 글머리 기호는 같은 점 직경의 평평한 점과 매우 유사합니다.초음속 사용을 위해 설계된 발사체는 종종 보트 꼬리라고 불리는 뒤쪽에 약간 테이퍼된 베이스를 가지고 있어서 비행 [38]시 공기 저항을 줄입니다.장거리 사격을 위한 "테이프로 된 후방"의 유용성은 1870년대 [39]초에 이미 잘 확립되었지만, 기술적인 어려움이 20세기에 들어서기 전에 그들의 광범위한 채택을 방해했습니다.발사체를 케이스에 안전하게 압착하는 데 사용되는 발사체 주위의 오목한 링인 캐넬루어는 드래그를 증가시킵니다.
분석 소프트웨어는 탄도 연구소(이후 육군 연구소로 불림)에서 개발한 것으로, 실제 시험 범위 데이터를 발사체 항력 계수 [40]예측을 위한 매개 변수 관계로 축소했습니다.대구경 포병은 기하학을 능률화하는 것 외에도 항력 감소 메커니즘을 사용합니다.로켓 보조 발사체는 공기역학적 항력을 극복하기 위해 추가 추력을 제공하는 입마개 출구에서 점화되는 작은 로켓 모터를 사용합니다.로켓 보조는 아음속 포탄 발사체에 가장 효과적입니다.기저 항력이 지배적인 초음속 장거리포의 경우 기저 블리딩이 사용됩니다.베이스 블리드는 가스 발생기의 한 형태로, 상당한 추력을 제공하지 않고 오히려 발사체 뒤의 저압 영역을 가스로 채워 베이스 드래그와 전체 발사체 드래그 계수를 효과적으로 감소시킵니다.
천음속 문제
초음속 주둥이 속도로 발사된 발사체는 어느 순간 음속에 접근하는 속도가 느려집니다.천음속 영역(약 마하 1.2–0.8)에서 대부분의 비구면 발사체의 압력 중심(CP)은 발사체가 감속함에 따라 앞으로 이동합니다.CP 이동은 발사체의 (동적) 안정성에 영향을 미칩니다.발사체가 잘 안정화되지 않으면 천음속 영역을 통해 전방을 향해 있을 수 없습니다(발사체는 감쇠되지 않으면 결국 길이 축을 따라 제어할 수 없는 텀블링으로 끝날 수 있는 한계 주기 요라고 불리는 원치 않는 세차 운동 또는 콘 모션을 보이기 시작합니다).그러나, 발사체가 천음속 영역을 통과하여 비행할 수 있을 정도로 충분한 안정성(정적이고 동적)을 가지고 있고 전방을 향하더라도, 여전히 영향을 받습니다.아음속 영역에 진입할 때 발사체의 비행이 다시 잘 수행되더라도 불규칙하고 갑작스러운 CP 이동 및 동적 안정성의 (일시적) 감소는 상당한 분산(그리고 따라서 상당한 정확도 저하)을 일으킬 수 있습니다.이것은 천음속 영역에서 발사체의 탄도 행동을 정확하게 예측하는 것을 매우 어렵게 만듭니다.
이것 때문에, 사격수들은 보통 발사체가 여전히 [note 1]초음속일 정도로 충분히 가까운 목표물을 교전하는 것으로 스스로를 제한합니다.2015년 미국의 탄도학자 브라이언 리츠는 초음속 발사(총탄) 탄환이 초음속 영역으로 들어가는 범위에서의 소총 사격을 정의하기 위해 "확장 장거리" 개념을 도입했습니다.Litz에 따르면, "장거리 연장은 총알이 초음속 범위로 느려질 때마다 시작됩니다.탄환이 마하 1에 가까워질 때 속도가 느려지면서 탄환이 상대적으로 [41]잘 작동하는 초음속 범위에 비해 더 복잡하고 설명하기 어려운 초음속 효과와 마주치기 시작합니다."
주변 공기 밀도는 천음속 전환 시 동적 안정성에 상당한 영향을 미칩니다.주변 공기 밀도는 가변적인 환경 요인이지만, 밀도가 낮은 공기를 통과하는 발사체는 밀도가 높은 공기를 통과하는 것보다 부정적인 초음속 전환 효과를 더 잘 부정할 수 있습니다.발사체 또는 탄환 길이도 한계 주기 요에 영향을 미칩니다.긴 발사체는 같은 직경의 짧은 발사체보다 더 많은 한계 주기 요를 경험합니다.불필요한 한계 주기 요 운동에 영향을 미치는 것으로 확인된 발사체 설계의 또 다른 특징은 발사체의 기저부에 있는 모따기입니다.발사체나 탄환의 맨 밑부분이나 뒤꿈치에는 0.25~0.50mm(0.01~0.02인치)의 모따기 또는 반지름이 있습니다.이 반지름의 존재는 발사체가 더 큰 한계 주기 요 [42]각도로 비행하도록 합니다.리플링은 제한 사이클 [43]요에도 미묘한 영향을 미칠 수 있습니다.일반적으로 고속 회전 발사체는 제한 주기 요를 덜 경험합니다.
유도탄 연구
스핀 안정화된 발사체가 직면한 천음속 문제를 피하기 위해 발사체는 이론적으로 비행 중에 유도될 수 있습니다.Sandia National Laboratory는 2012년 1월에 1마일(약 1,610m 또는 1760야드) 이상의 거리에서 레이저로 지정된 목표물을 타격할 수 있는 소구경 매끄러운 구경의 총기를 위한 4인치(102mm) 길이의 다트와 같은 자체 유도 총알을 연구하고 시험 발사했다고 발표했습니다.이 발사체들은 스핀 안정화되지 않으며 비행 경로는 초당 30회 전자 작동기로 제한 내에서 조종할 수 있습니다.연구원들은 또한 총알이 총신을 빠져나올 때 급진적으로 투구하고 사정거리를 내려갈 때 적게 투구하는 비디오를 가지고 있다고 주장하는데, 이는 장거리 총기 전문가들에게 "잠드는 것"으로 알려진 논쟁적인 현상입니다.샌디아 연구원 레드 존스는 총알의 움직임이 비행 시간이 길수록 안정되기 때문에 더 긴 거리에서 정확도가 향상된다고 말했습니다."아무도 그것을 본 적이 없지만, 우리는 그것이 사실이라는 것을 보여주는 고속 비디오 사진을 가지고 있습니다," 라고 그가 말했습니다.[44]최근 테스트에 따르면 초기 작동 [45]성능이 근접했거나 이미 달성된 것으로 나타났습니다.
소프트웨어의 예측 품질 테스트
비행의 모든 변수를 사전에 알고 보상할 수 없기 때문에 아무리 발전된 소프트웨어 시뮬레이션은 항상 실제 궤도와 완벽하게 일치하는 예측을 산출하지 못할 것입니다.그러나 실제 비행 행동에 매우 가까운 예측을 얻을 수 있습니다.
경험적 측정법
(극단적인) 장거리용 탄도 예측 컴퓨터 프로그램은 초음속에서 아음속 전환 범위(소총/카트리지/총탄 조합의 초음속 범위의 마지막 10~20%)에서 현장 테스트를 수행하여 평가할 수 있습니다.예를 들어 표준 16.2g(250gr) Lapua Scenar GB488 탄환을 905m/s(2969ft/s)의 총구 속도로 사격하는 일반적인 .338 Lapua Magnum 소총의 경우, 소프트웨어의 현장 시험은 국제 표준 대기 해수면 조건(공기 밀도 ρ = 1.225kg/m)에서 1300 1200-1422m(1312-1422yd)에서 수행해야 합니다.소프트웨어가 짧은 범위에서 중간 범위까지의 궤적을 얼마나 잘 예측하는지 확인하려면 초음속 범위의 20, 40, 60%에서 현장 테스트를 수행해야 합니다.중간 범위보다 짧은 범위에서는 천음속 문제와 그에 따라 행동하지 않는 총알 비행이 발생해서는 안 되며 BC는 일시적일 가능성이 적습니다.(극단적인) 장거리에서 소프트웨어의 예측 품질을 테스트하는 것은 탄약을 소비하기 때문에 비용이 많이 듭니다. 통계적으로 신뢰할 수 있는 진술을 하기 위해서는 발사된 모든 총의 실제 총구 속도를 측정해야 합니다.24개 미만의 표본 그룹은 원하는 통계적으로 유의한 신뢰 구간을 얻지 못할 수 있습니다.
도플러 레이더 측정법
정부, 전문 탄도학자,방위군 및 일부 탄약 제조업체는 대형 발사체에 장착된 도플러 레이더 및/또는 원격 측정 프로브를 사용하여 관심 있는 특정 발사체의 비행 행동에 관한 정확한 실제 데이터를 확보하고, 따라서 수집된 실제 데이터를 탄도 컴퓨터 프로그램에 의해 계산된 예측과 비교합니다.그러나 일반적인 사격이나 공기역학 애호가들은 그런 값비싼 전문 측정 장치를 사용할 수 없습니다.당국과 발사체 제조업체는 일반적으로 도플러 레이더 테스트 결과와 발사체의 시험 유도 항력 계수(Cd)를 일반 대중과 공유하는 것을 꺼립니다.2020년경, 무료 비행 항력 계수를 결정하기 위해 더 저렴하지만 성능이 떨어지는 (아마추어) 도플러 레이더 장비가 일반 [46]대중에게 제공되었습니다.
2009년 1월, 스칸디나비아 탄약 제조업체인 Nammo/Lapua는 대부분의 소총 [47][48]발사체에 대한 도플러 레이더 시험 파생 항력 계수 데이터를 발표했습니다.2015년 미국의 탄약 제조업체인 버거 불릿은 PRODAS 6 DoF 소프트웨어와 함께 도플러 레이더를 사용하여 궤적 [49]솔루션을 생성한다고 발표했습니다.2016년 미국 탄약 제조업체 호나디는 궤도 솔루션을 [50][51][52][53]생성하기 위해 수정된 포인트 질량 모델을 사용하는 소프트웨어에 도플러 레이더 유도 드래그 데이터를 사용한다고 발표했습니다.측정을d 통해 파생된 C 데이터 엔지니어는 알려진 수학적 탄도 모델과 특정 표 형식의 데이터를 동시에 테스트하는 알고리즘을 만들 수 있습니다.QuickTARGET Unlimited, Lapua Edition,[54] Lapua[55] Ballistics 또는 Hornady 4DOF와 같은 예측 소프트웨어에서 사용할 경우 도플러 레이더 테스트에서 파생된 항력 계수 데이터를 사용하여 보다 정확한 외부 탄도 예측을 수행할 수 있습니다.
Lapua에서 제공한 항력 계수 데이터 중 일부는 마하 1 비행 속도 영역 주변 또는 그 이하에서 측정된 항력이 급격하게 증가함을 보여줍니다.이 동작은 대부분의 측정된 소구경 총알에서 관찰되었으며, 대구경 총알에서는 관찰되지 않았습니다.이는 일부(대부분 더 작은 구경의) 소총 탄환이 천음속/아음속 비행 속도 체제에서 더 많은 제한 주기 요(코닝 및/또는 텀블링)를 나타냈음을 의미합니다.일부 시험 발사체에 대한 부정적인 천음속/아음속 비행 거동에 관한 정보는 중요합니다.한계 주기 요의 효과는 쉽게 예측할 수 없고 최상의 탄도 예측 모델 및 소프트웨어에 치명적일 수 있기 때문에 이는 장거리 사격 사용에 대한 제한 요소입니다.
제시된d C 데이터는 라푸아 테스터가 시험 발사 동안 사용한 배럴, 회전(회전) 속도 및 탄약 로트에 대해 측정되었기 때문에 모든 총기-탄약 조합에 단순히 사용할 수 없습니다.라이플링의 차이(홈의 수, 깊이, 폭 및 기타 치수 특성), 비틀림 속도 및/또는 총구 속도와 같은 변수는 발사체에서 서로 다른 회전(스핀) 속도 및 라이플링 마크를 제공합니다.이러한 변수의 변화와 발사체 생산 로트의 변화는 발사체가 통과하는 공기와의 서로 다른 다운 레인지 상호 작용을 발생시켜 비행 행동에 (작은) 변화를 초래할 수 있습니다.외부 탄도학의 이 특정 분야는 현재 (2009년) 자세히 연구되지 않았거나 [56]잘 이해되지 않았습니다.
여러 항력 모델링 및 측정 방법의 예측
외부 탄도 행동을 모델링하고 예측하기 위해 사용되는 방법은 비행 범위와 시간이 증가함에 따라 다른 결과를 산출할 수 있습니다.이를 설명하기 위해 Lapua Scenar GB528 19.44 g (300 gr) 8.59 mm (0.338 in) 제조업체가 G1 탄도 계수(BC)를 0으로 표시한 매우 낮은 항력 소총 탄환을 보정합니다.국제 표준 대기 해수면 조건(공기 밀도 θ = 1.225 kg/m³)에서 830 m/s(2723 ft/s)의 총구 속도로 발사된 785발은 마하 1 = 340.3 m/s, 마하 1.2 = 408.4 m/s)로 발사되며, 발사체 속도와 비행 시간은 0 ~ 3,000 m(0 ~ 3,281 yd)[note 2]로 예측되었습니다.
| 범위(m) | 0 | 300 | 600 | 900 | 1,200 | 1,500 | 1,800 | 2,100 | 2,400 | 2,700 | 3,000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 레이더 테스트 파생 항력 계수 방법 V(m/s) | 830 | 711 | 604 | 507 | 422 | 349 | 311 | 288 | 267 | 247 | 227 |
| 비행 시간 | 0.0000 | 0.3918 | 0.8507 | 1.3937 | 2.0435 | 2.8276 | 3.7480 | 4.7522 | 5.8354 | 7.0095 | 8.2909 |
| 총강하량(m) | 0.000 | 0.715 | 3.203 | 8.146 | 16.571 | 30.035 | 50.715 | 80.529 | 121.023 | 173.998 | 241.735 |
| 6 DoF 모델링 방법 V(m/s) | 830 | 711 | 604 | 506 | 420 | 347 | 310 | 287 | 266 | 244 | 222 |
| 비행 시간 | 0.0000 | 0.3919 | 0.8511 | 1.3949 | 2.0467 | 2.8343 | 3.7575 | 4.7641 | 5.8508 | 7.0332 | 8.3346 |
| 총강하량(m) | 0.000 | 0.714 | 3.195 | 8.132 | 16.561 | 30.060 | 50.836 | 80.794 | 121.498 | 174.796 | 243.191 |
| G1 드래그 모델 방법 V(m/s) | 830 | 718 | 615 | 522 | 440 | 374 | 328 | 299 | 278 | 261 | 248 |
| 비행 시간 | 0.0000 | 0.3897 | 0.8423 | 1.3732 | 2.0009 | 2.7427 | 3.6029 | 4.5642 | 5.6086 | 6.7276 | 7.9183 |
| 총강하량(m) | 0.000 | 0.710 | 3.157 | 7.971 | 16.073 | 28.779 | 47.810 | 75.205 | 112.136 | 160.739 | 222.430 |
| Pejsa 항력 모형 방법 V(m/s) | 830 | 712 | 603 | 504 | 413 | 339 | 297 | 270 | 247 | 227 | 208 |
| 비행 시간 | 0.0000 | 0.3902 | 0.8479 | 1.3921 | 2.0501 | 2.8556 | 3.8057 | 4.8682 | 6.0294 | 7.2958 | 8.6769 |
| 총강하량(m) | 0.000 | 0.719 | 3.198 | 8.129 | 16.580 | 30.271 | 51.582 | 82.873 | 126.870 | 185.318 | 260.968 |
| G7 드래그 모델 방법 V (m/s) | 830 | 713 | 606 | 508 | 418 | 339 | 303 | 283 | 265 | 249 | 235 |
| 비행 시간 | 0.0000 | 0.3912 | 0.8487 | 1.3901 | 2.0415 | 2.8404 | 3.7850 | 4.8110 | 5.9099 | 7.0838 | 8.3369 |
| 총강하량(m) | 0.000 | 0.714 | 3.191 | 8.109 | 16.503 | 30.039 | 51.165 | 81.863 | 123.639 | 178.082 | 246.968 |
표는 도플러 레이더 테스트 파생 드래그 계수(Cd) 예측 방법과 2017년 Lapua Ballistics 6 DoF App 예측이 유사한 결과를 생성하는 것을 보여줍니다.6 DoF 모델링은 이 총알에 대해 2,400m(2,625yd) 이상의 범위에서 과도한 안정화로 끌리는 총알 안정성(((Sd) 및 (Sg)을 추정합니다.2,400m(2,625yd)에서 총 낙하 예측은 50° 위도에서 47.5cm(19.7인치) 또는 0.20m(0.68moa)를 벗어나며, 최대 2,700m(2,953yd)까지 총 낙하 예측은 50° 위도에서 0.30m(1moa) 이내입니다.2016년 Lapua Ballistics 6 DoF App 버전 예측은 도플러 레이더 테스트 예측에 훨씬 더 가까웠습니다.
전통적인 Siacci/Mayevski G1 드래그 곡선 모델 예측 방법은 일반적으로 현대의 도플러 레이더 테스트 파생 드래그 계수(Cd) 예측 [note 3]방법에 비해 더 낙관적인 결과를 산출합니다.300m(328yd) 범위에서는 차이가 거의 눈에 띄지 않지만 600m(656yd) 이상에서는 차이가 10m/s(32.8ft/s)의 투사 속도에 걸쳐 커지고 점차 현저해집니다.1,500 m(1,640 yd) 범위에서 발사체 속도 예측은 25 m/s(82.0 ft/s)를 벗어나며, 이는 50° 위도에서 125.6 cm(49.4 in) 또는 0.83 m(2.87 ma)의 예상 총 낙하 차이와 같습니다.
경사 상수 인자 미세 조정이 없는 페이사 드래그 모델 폐쇄형 솔루션 예측 방법은 도플러 레이더 테스트 파생 드래그 계수(Cd) 예측 방법과 비교하여 초음속 비행 체제에서 매우 유사한 결과를 산출합니다.1,500 m(1,640 yd) 범위에서 발사체 속도 예측은 10 m/s(32.8 ft/s)를 벗어나며, 이는 50° 위도에서 23.6 cm(9.3 in) 또는 0.16 m(0.54 ma)의 예상 총 낙하 차이와 같습니다.
0.377의 G7 탄도 계수(BC)를 사용할 때 G7 드래그 곡선 모델 예측 방법(일부 제조업체에서 매우 낮은 드래그 모양 소총 탄환에 대해 권장)은 도플러 레이더 테스트 파생 드래그 계수(Cd) 예측 방법과 비교하여 초음속 비행 체제에서 매우 유사한 결과를 산출합니다.1,500m(1,640yd) 범위에서 발사체 속도 예측의 최대 편차는 10m/s(32.8ft/s)입니다.1,500m(1,640yd)에서 예상되는 총 강하 차이는 50° 위도에서 0.4cm(0.16in)입니다.1,800m(1,969yd)에서 예상되는 총 강하 차이는 45.0cm(17.7in)이며, 이는 0.25m(0.86moa)와 같습니다.
적절한 예측 모델은 초음속 비행 체제에서 유사한 결과를 산출할 것으로 예상됩니다.1,200m(1,312yd) 이하의 5가지 예제 모델은 모두 초음속 마하 1.2+ 발사체 속도와 51cm(20.1in) 대역폭 내의 총 낙하 차이를 예측합니다.1,500m(1,640yd)의 초음속 비행 체제에서 모델은 마하 1.0 ~ 마하 1.1 부근의 발사체 속도와 훨씬 큰 150cm(59인치) 대역폭 내의 총 낙하 차이를 예측합니다.
외부 요인
바람
바람에는 다양한 효과가 있으며, 첫 번째는 발사체가 옆으로 빗나가도록 하는 효과입니다(수평 편향).과학적인 관점에서 볼 때, "발사체의 측면을 밀어내는 바람"은 수평적인 바람 드리프트를 유발하는 것이 아닙니다.바람의 이동을 유발하는 것은 항력입니다.항력은 풍향계와 마찬가지로 발사체를 바람으로 바꾸어 공기 압력의 중심을 코에 유지시킵니다.이것은 코가 바람 속으로 (당신의 관점에서) 꼬이게 하고, 베이스는 (당신의 관점에서) "바람 아래로" 꼬이게 합니다.그래서 (여러분의 관점에서도) 드래그는 발사체를 바람을 타고 아래쪽으로 코에서 꼬리 방향으로 밀어내는 것입니다.
바람은 또한 공기역학적 점프를 유발하는데, 이는 발사체의 자유로운 비행 또는 주둥이 또는 매우 가까운 곳에서 활성화된 횡방향(바람) 임펄스에 의해 발생하여 동적 [57]불균형을 초래합니다.공기역학적 점프의 양은 교차 풍속, 총구에서 총알의 자이로스코프 안정성, 총구 비틀림이 시계방향 또는 반시계방향인지에 따라 달라집니다.바람 방향과 마찬가지로 비틀림 방향이 공기역학적 점프 방향을 역전시킵니다.
다소 덜 명백한 효과는 역풍 또는 순풍에 의해 발생합니다.역풍은 발사체의 상대 속도를 약간 증가시키고 항력과 그에 상응하는 강하를 증가시킵니다.순풍은 항력과 발사체/탄환 낙하를 감소시킵니다.바람은 힘과 방향이 거의 일정하지 않고 일반적으로 불어오는 지형과 상호 작용하기 때문에 실제 세계에서 순한 역풍이나 순풍은 거의 없습니다.이로 인해 역풍 또는 순풍 조건에서 초장거리 사격이 어려운 경우가 많습니다.
수직각
샷의 수직 각도(또는 높이)도 샷의 궤적에 영향을 미칩니다.소형 구경 발사체(권총 또는 소총에서 발사됨)를 위한 탄도 테이블은 지면에 수직으로 작용하는 중력으로 사격자와 표적 사이의 수평 시선을 가정합니다.따라서 사격자 대 표적 각도가 위 또는 아래인 경우(중력 성분의 방향이 기울기 방향에 따라 변하지 않음), 중력으로 인한 궤적 곡선 가속도는 경사각의 코사인에 비례하여 실제로 더 작을 것입니다.결과적으로 소위 "사선 범위"에서 위쪽 또는 아래쪽으로 발사된 발사체는 평평한 지면에서 동일한 목표 거리를 초과 사격하게 됩니다.그 효과는 충분히 커서 사냥꾼들은 산악 지형에서 그들의 목표 연기를 적절히 조정해야 합니다.수평 범위 홀드오프에 대한 기울기 범위 조정을 위한 잘 알려진 공식은 라이플맨의 규칙으로 알려져 있습니다.라이플맨 규칙과 약간 더 복잡하고 덜 알려진 개량 라이플맨 규칙 모델은 많은 소형 무기 응용에 대한 충분히 정확한 예측을 생성합니다.그러나 간단한 예측 모델은 오르막 또는 내리막을 촬영할 때 사소한 중력 효과를 무시합니다.이를 보완할 수 있는 유일한 실질적인 방법은 탄도 컴퓨터 프로그램을 사용하는 것입니다.장거리에 걸쳐 매우 가파른 각도에서의 중력 외에도, 공기 밀도의 영향은 비행 중에 만나는 발사체를 변화시키는 [58]것이 문제가 됩니다.경사 화재 시나리오에 사용할 수 있는 수학적 예측 모델은 경사 각도 및 범위의 양과 방향(상승 또는 하강)에 따라 다양한 정확도 예상 [59]수준을 산출합니다.덜 발달된 탄도 컴퓨터 프로그램은 동일한 수직 각도와 범위에서 오르막과 내리막 샷에 대해 동일한 궤적을 예측합니다.더 발전된 프로그램은 오르막과 내리막 샷에서 중력의 작은 효과를 고려하여 동일한 수직 각도와 범위에서 약간 다른 궤적을 만듭니다.현재 공개적으로 이용 가능한 탄도 컴퓨터 프로그램(2017)은 발사체가 비행 중에 만나는 공기 밀도가 다른 복잡한 현상을 설명하지 않습니다.
주변 공기 밀도
기압, 온도 및 습도 변화가 주변 공기 밀도를 구성합니다.습도는 반직관적인 영향을 미칩니다.수증기의 밀도는 리터당 0.8g인 반면 건조한 공기는 리터당 평균 약 1.225g이기 때문에 습도가 높을수록 실제로 공기 밀도가 감소하고 따라서 저항이 감소합니다.
강수
총탄이 빗방울과 충돌할 때 강수량은 상당한 요와 그에 따른 편향을 일으킬 수 있습니다.이러한 우연한 충돌이 발생하는 범위가 더 낮을수록 대상에 대한 편향은 줄어듭니다.빗방울과 총알의 무게는 그러한 충돌 동안 요가 유도되는 정도에도 영향을 미칩니다.큰 빗방울과 가벼운 총알은 최대 요 효과를 낼 것입니다.같은 빗방울과 충돌하는 무거운 총알은 요 [60]효과를 크게 덜 경험할 것입니다.
장거리 요인
자이로스코프 드리프트(회전 드리프트)
자이로스코프 드리프트는 총알의 질량과 공기역학이 비행하는 대기와 상호작용하는 것입니다.측면 공기의 움직임이 전혀 없는 완전히 조용한 공기에서도 스핀 안정화된 발사체는 "휴식의 요"로 알려진 자이로스코프 현상으로 인해 스핀에 의한 측면 구성 요소를 경험하게 됩니다.오른쪽(시계 방향) 회전의 경우 이 구성 요소는 항상 오른쪽에 있습니다.왼쪽(시계 반대 방향) 회전의 경우 이 구성 요소는 항상 왼쪽에 있습니다.이는 발사체의 세로축(회전축)과 무게중심(CG)의 속도 벡터 방향이 작은 각도만큼 어긋나기 때문인데, 이를 평형요 또는 휴지요라고 합니다.휴식 각도의 요 크기는 일반적으로 0.[61]5도 미만입니다.회전하는 물체는 인가된 토크 벡터로부터 90도 각도의 각속도 벡터와 반응하기 때문에, 탄환의 대칭축은 수직면의 구성요소와 수평면의 구성요소와 함께 이동합니다; 오른손(시계방향) 회전 탄환의 경우,탄환의 대칭축은 발사체가 탄도 호를 따라 이동할 때 속도 벡터의 방향을 기준으로 오른쪽으로 약간 위쪽으로 치우칩니다.이 작은 경사의 결과로, 지속적인 기류가 형성되어 총알이 오른쪽으로 빗나가는 경향이 있습니다.따라서 탄환이 오른쪽(오른손 회전) 또는 왼쪽(왼손 회전)으로 이동하는 이유는 휴식의 요(Yaw of rese)가 발생하기 때문입니다.이것은 총알이 주어진 순간에 옆으로 미끄러지고, 따라서 옆으로 미끄러지는 [62][63]성분을 경험한다는 것을 의미합니다.
다음 변수는 자이로스코프 드리프트의 크기에 영향을 미칩니다.
- 발사체 또는 탄환 길이: 긴 발사체는 주어진 요 각도에 대해 더 많은 측면 "리프트"를 생성하기 때문에 자이로스코프 드리프트를 경험합니다.
- 회전 속도: 더 빠른 회전 속도는 코가 더 먼 쪽을 가리키기 때문에 자이로스코프 드리프트를 더 많이 생성합니다.
- 범위, 비행 시간 및 궤적 높이: 자이로스코프 드리프트는 이러한 모든 변수에 따라 증가합니다.
- 대기의 밀도: 밀도가 높은 공기는 자이로스코프 드리프트를 증가시킵니다.
1000야드(914.4m)에서 미군 및 기타 초저저항 탄환의 자이로스코프 드리프트에 대한 도플러 레이더 측정 결과는 다음과 같습니다.
| 글머리 기호 | 미군 M193볼 (5.56x45mm NATO) | 미군 M118 스페셜볼 (7.62x51mm NATO) | 팔마 시에라 매치 킹 | LRBT J40 매치 | 시에라 매치 킹 | 시에라 매치 킹 | LRBT J40 매치 | LRBT J40 매치 |
|---|---|---|---|---|---|---|---|---|
| 발사체 질량(곡물 및 g 단위) | 55알(3.56g) | 173알(11.21g) | 155알(10.04g) | 190알(12.31g) | 220알(14.26g) | 300알(19.44g) | 350알(22.68g) | 419알(27.15g) |
| 투사체 직경(인치 및 mm 단위) | .224인치(5.69mm) | .308인치(7.82mm) | .308인치(7.82mm) | .308인치(7.82mm) | .308인치(7.82mm) | .338인치(8.59mm) | .198인치(9.53mm) | .408인치(10.36mm) |
| 자이로스코프 드리프트(인치 및 mm 단위) | 23.00인치(584.20mm) | 11.50인치(292.10mm) | 12.75인치(323.85mm) | 3.00인치(76.20mm) | 7.75인치(165.85mm) | 6.50인치(165.10mm) | 0.87인치(22.10mm) | 1.90인치(48.26mm) |
표는 자이로스코프 드리프트를 무게와 직경만으로 예측할 수 없음을 보여줍니다.자이로스코프 드리프트에 대한 정확한 예측을 하기 위해서는 외부 및 내부 탄도에 대한 몇 가지 세부 사항이 고려되어야 합니다.포신의 비틀림 속도, 포신이 총구를 빠져나올 때의 속도, 포신 고조파 및 대기 조건과 같은 요소들은 모두 발사체의 경로에 기여합니다.
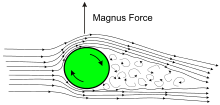
마그누스 효과
스핀 안정화된 발사체는 탄환의 스핀이 바람의 측면 벡터에 수직으로 위 또는 아래로 작용하는 힘을 생성하는 Magnus 효과의 영향을 받습니다.수평풍과 우측(시계방향) 회전 방향의 단순한 경우, 탄환 주위에 유도된 압력 차이는 발사 지점에서 본 아래쪽(오른쪽에서 부는 바람) 또는 위쪽(왼쪽에서 부는 바람) 힘을 발사체에 작용시켜 탄환의 충격 지점에 [64]영향을 줍니다.수직 편향 값은 수평 바람 유도 편향 요소에 비해 작은 경향이 있지만, 그럼에도 불구하고 4m/s(14.4km/h 또는 9mph)를 초과하는 바람에서는 상당할 수 있습니다.
매그너스 효과와 탄환 안정성
마그누스 효과는 탄환의 무게중심에 작용하는 것이 아니라 탄환의 요에 영향을 미치는 압력중심에 작용하기 때문에 탄환 안정성에 중요한 역할을 합니다.Magnus 효과는 무게 중심보다 앞쪽에 위치한 압력 중심을 가진 총알에 불안정한 힘으로 작용하고 반대로 무게 중심 뒤에 위치한 압력 중심을 가진 총알에 안정적인 힘으로 작용합니다.압력 중심의 위치는 유동장 구조, 즉 탄환이 초음속, 초음속 또는 아음속 비행 중인지에 따라 달라집니다.실제로 이것이 의미하는 바는 탄환의 모양과 다른 속성에 따라 달라지는데, 어떤 경우든 마그누스 힘은 탄환이 비행 [65][66]경로를 따라 "뒤틀려"고 시도하기 때문에 안정성에 큰 영향을 미칩니다.
역설적으로, 길이 때문에 매우 낮은 항력 탄환은 이동하는 공기에 더 큰 표면적을 제공하여 공기역학적 효율을 감소시키기 때문에 더 큰 Magnus 불안정 오류를 나타내는 경향이 있습니다.이러한 미묘한 효과는 형상 및 단면 밀도에 기초한 계산된d C 또는 BC가 제한적으로 사용되는 이유 중 하나입니다.
포아송 효과
궤도 위에 있는 발사체의 코에 따라 달라지는 표류의 또 다른 작은 원인은 포아송 효과입니다.이것은, 만약 그것이 일어난다면, 자이로스코프 드리프트와 같은 방향으로 작용하고 매그너스 효과보다 훨씬 덜 중요합니다.그것은 발사체의 위쪽 코가 공기 쿠션을 그 아래에 쌓이게 한다고 가정합니다.또한 이 쿠션과 발사체 사이에 마찰이 증가하여 후자가 회전하면서 쿠션에서 굴러 떨어져 옆으로 이동하는 경향이 있다고 가정합니다.
이 간단한 설명은 꽤 인기가 있습니다.그러나 압력이 증가하면 마찰력이 증가한다는 것을 보여주는 증거가 없으며 그렇지 않으면 효과가 없습니다.그것이 존재한다고 해도 자이로스코프 및 코리올리 드리프트에 비해 상당히 미미할 것입니다.
코가 궤적 아래로 떨어지면 포아송 효과와 매그너스 효과 모두 드리프트 방향을 반대로 합니다.평형 요에서처럼 코가 한쪽으로 쏠리면 이러한 효과가 범위에 미세한 변화를 일으킵니다.
코리올리 표류
코리올리 효과는 지구 축에 수직인 방향으로 코리올리 드리프트를 발생시킵니다. 지구 및 발사 방향의 대부분의 위치에서 이 편향은 수평 및 수직 구성 요소를 포함합니다.편차는 북반구의 궤적 오른쪽, 남반구의 왼쪽, 동쪽 사격의 경우 위쪽, 서쪽 사격의 경우 아래쪽입니다.수직 코리올리 편향은 외트뵈시 효과라고도 합니다.코리올리 드리프트는 공기역학적 효과가 아닙니다; 그것은 지구의 자전의 결과입니다.
코리올리 효과의 크기는 작습니다.소형 무기의 경우, 코리올리 효과의 크기는 일반적으로 미미하지만(1,000 m (1,094 yd)에서 약 10 cm (3.9 in) 정도의 고출력 소총의 경우), 대륙간 탄도 미사일과 같은 극한의 장거리 소총 발사체, 포, 로켓과 같이 비행 시간이 긴 탄도 발사체의 경우,궤적을 계산하는 데 중요한 요소입니다.드리프트의 크기는 발사 및 목표 위치, 발사 방위, 발사체 속도 및 비행 시간에 따라 달라집니다.
수평효과
회전하지 않는 기준 프레임(즉, 지구와 함께 회전하는 기준 프레임이 아님)에서 볼 때, 중력과 공기 저항을 무시하고 발사체는 직선으로 움직입니다.지구에 대해 고정된 기준 프레임에서 볼 때, 그 직선 궤적은 옆으로 구부러진 것처럼 보입니다.이 수평 곡률의 방향은 북반구에서는 오른쪽이고 남반구에서는 왼쪽이며, 샷의 방위에 의존하지 않습니다.수평 곡률은 극점에서 가장 크고 [67]적도에서는 0으로 감소합니다.
수직(외트뵈시 효과
외트뵈시 효과는 운동 방향과 속도, 지구 [68][69]자전 방향 사이의 관계에 기초하여 움직이는 물체에 대한 인식된 중력을 변화시킵니다.
외트뵈시 효과는 적도에서 가장 크고 극에서는 0으로 감소합니다.그것은 동쪽으로 이동하는 발사체가 위쪽으로 방향을 틀게 하고, 서쪽으로 이동하는 발사체가 아래쪽으로 방향을 틀게 합니다.다른 방향의 궤적에 대해서는 효과가 덜 뚜렷하며, 정북 또는 남향을 목표로 하는 궤적에 대해서는 0입니다.우주선이 지구 궤도로 발사되는 것과 같은 큰 운동량 변화의 경우, 그 효과는 상당합니다.그것은 궤도로 가는 가장 빠르고 연료 효율적인 경로에 기여합니다: 적도에서 곧장 동쪽으로 향하는 발사입니다.
장비 요인
발사체 궤도에 작용하는 힘은 아니지만 궤도에 영향을 미치는 장비 관련 요소가 몇 가지 있습니다.이러한 요인들은 달리 설명할 수 없는 외부 탄도 비행 행동을 유발할 수 있기 때문에 간략하게 언급해야 합니다.
가로뛰기
측면 점프는 발사 순간 총신의 약간의 측면 및 회전 운동에 의해 발생합니다.베어링에 작은 오차가 발생하는 효과가 있습니다.크기가 작고 라운드마다 다르기 때문에 효과는 무시됩니다.
측면 방출
수평 방출은 적용된 스핀 안정화된 발사체의 질량 불균형 또는 발사체가 총신을 축에서 벗어나 정적 불균형으로 이어질 때 과도 비행 단계 동안 압력 불균형으로 인해 발생합니다.존재할 경우 분산이 발생합니다.일반적으로 크기가 작고 발사체에서 발사체로, 원형에서 원형으로, 총신에서 총신으로 다양하기 때문에 효과를 예측할 수 없습니다.
최대 유효 소형 암 범위
모든 소형 무기와 특히 고성능 저격총의 최대 실용[note 4] 범위는 주로 사용되는 스핀 안정 발사체의 공기역학적 또는 탄도 효율에 따라 달라집니다.장거리 사격 선수들은 또한 지점 목표물에서 첫 번째 샷을 날릴 수 있도록 고도와 바람의 보정을 계산하기 위해 관련 정보를 수집해야 합니다.이러한 화재 제어 보정을 계산하는 데이터에는 다음과 같은 [70]변수의 긴 목록이 있습니다.
- 탄도 계수 또는 시험 파생 항력 계수(Cd)/사용된 탄환의 거동
- 라이플 보어 축 위의 조준 구성 요소 높이
- 조준 구성 요소와 라이플 조합이 관찰된 0 범위
- 탄환의 질량
- 실제 총구 속도(분말 온도가 총구 속도에 영향을 미치며 프라이머 점화도 온도에 따라 다름)
- 사거리에서 목표물까지
- 사용된 총, 탄약 및 탄환 조합의 초음속 범위
- 오르막/내리막 사격 시 경사각
- 목표 속도와 방향
- 풍속 및 방향(수평 발사체 편향의 주요 원인이며 일반적으로 정확하게 측정하고 판단하기 어려운 탄도 변수).바람 효과로 인해 수직 편향이 발생할 수도 있습니다.)
- 기압, 온도, 고도 및 습도 변화(주위 공기 밀도를 구성함)
- 지구 중력(위도 및 고도에 따라 약간 변화)
- 자이로스코프 드리프트(배럴의 비틀림 방향과 비틀림 속도에 의해 유도되는 수평면 및 수직면 자이로스코프 효과(종종 스핀 드리프트로 알려져 있음)
- 코리올리 효과 드리프트(위도, 화재 방향 및 북반구 또는 남반구 데이터가 이 효과를 지시함)
- 외트뵈시 효과(코리올리 효과, 위도 및 화재 방향과 상호 관련이 있음)
- 공기역학적 점프(자유 비행 중 또는 동적 [57]불균형을 초래하는 주둥이 또는 매우 가까운 곳에서 활성화된 횡방향(바람) 임펄스에 의해 발생하는 횡풍 편향의 수직 구성 요소)
- 측면 방출(적용된 발사체의 질량 불균형으로 인해 발생하거나 배럴이 축을 벗어나 정적 불균형이 발생하는 변형)
- 조준 구성 요소의 고유 잠재적 정확도 및 조정 범위
- 소총의 고유 잠재적 정확도
- 탄약의 고유 잠재적 정확도
- 궤적 계산에 사용되는 컴퓨터 프로그램 및 기타 사격 제어 구성 요소의 고유 잠재적 정확도
주변 공기 밀도는 북극 해수면 조건에서 최대치입니다.차가운 화약은 또한 낮은 압력을 생성하여 따뜻한 화약보다 낮은 총구 속도를 만듭니다.이것은 총의 최대 실용 범위가 북극 해수면 조건에서 가장 짧을 것이라는 것을 의미합니다.
원거리에서 지점 목표물을 타격할 수 있는 능력은 환경적, 기상학적 요인을 다루는 능력과 외부 탄도 및 장비의 한계에 대한 이해와 많은 관련이 있습니다.탄도 솔루션을 결정하는 데 도움이 되는 (컴퓨터) 지원과 매우 정확한 레이저 거리 측정기 및 기상 측정 장비가 없다면, 알려지지 않은 범위에서 1000m(1100yd) 이상의 장거리 사격은 심지어 가장 전문적인 장거리 사격 [note 5]기술자에게도 추측이 됩니다.
흥미로운 추가 읽기: 마크맨십 위키북
탄도 데이터 사용
다음은 0.480 BC의 .30 칼리브 Speer 169 그레인(11g)의 뾰족한 보트 꼬리 매치 탄환에 대한 탄도 표의 예입니다.보어 라인 위 1.5인치(38mm)의 조준경과 조준경이 각각 200야드(183m)와 300야드(274m)와 일치하도록 조정된 조준경을 가정합니다.
| 범위 | 0 | 100야드 91m | 200야드 183m | 300야드 274m | 400야드 366m | 500야드 457m | |
|---|---|---|---|---|---|---|---|
| 속도 | (ft/s) | 2,700 | 2,512 | 2,331 | 2,158 | 1,992 | 1,834 |
| (m/s) | 823 | 766 | 710 | 658 | 607 | 559 | |
| 200야드/184m에 대해 영점 조정 | |||||||
| 높이 | (in) | −1.5 | 2.0 | 0 | −8.4 | −24.3 | −49.0 |
| (mm) | −38 | 51 | 0 | −213 | −617 | −1245 | |
| 274m/300야드에 대해 영점 조정 | |||||||
| 높이 | (in) | −1.5 | 4.8 | 5.6 | 0 | −13.1 | −35.0 |
| (mm) | −38 | 122 | 142 | 0 | −333 | −889 | |
이 표는 상당히 공기역학적인 총알이 고속으로 발사되더라도 "탄환 낙하" 또는 충격 지점의 변화가 상당함을 보여줍니다.이러한 영향 지점의 변화는 두 가지 중요한 의미를 갖습니다.첫째, 400~500yd(460m)의 충격 지점 차이가 25~32in(0에 따라 다름)이기 때문에 더 긴 범위에서 목표물까지의 거리를 추정하는 것이 중요합니다.즉, 사격 선수가 목표물이 실제로 500yd 떨어져 있을 때 목표물이 400yd 떨어져 있다고 추정할 경우, 목표물 아래 25-32인치(635-813mm)에 충격을 주어 목표물을 완전히 놓칠 수 있습니다.두 번째로, 소총은 일반적인 표적 범위에 적합한 거리로 영점을 맞춰야 합니다. 왜냐하면 사격자는 큰 총알 낙하를 보상하기 위해 표적 위에서 멀리 조준해야 할 수 있기 때문에 표적을 완전히 볼 수 없습니다(예: 망원경 시야 밖에 있을 수 있습니다).200yd(180m)에서 영점을 맞춘 라이플의 예에서, 사격 선수는 500yd에서 목표물에 대해 충돌 지점으로부터 4피트(1.2m) 이상 위에서 49를 조준해야 합니다.
참고 항목
- 내부 탄도학 - 발사체와 추진체가 배럴을 떠나기 전의 거동.
- 과도 탄도학 - 발사체가 총구를 떠날 때부터 발사체 뒤의 압력이 균등화될 때까지의 발사체의 동작입니다.
- 단자 탄도 - 목표물과의 충돌 시 발사체의 거동.
- 발사체의 궤적 - 기본 외부 탄도 수학 공식.
- 라이플맨의 규칙 - 라이플맨이 오르막 또는 내리막 거리에서 목표를 조준하기 위한 절차 또는 "규칙".
- Franklin Ware Mann - 외부 탄도에 대한 초기 과학적 연구.
- 권총 및 소총 탄약 목록
- 조준 위치 - 조준점이 주어진 거리에서 궤적과 교차하도록 원거리 무기의 조준점을 보정하여 사용자가 조준 대상을 지속적으로 타격할 수 있도록 합니다.
메모들
- ^ 동적 안정성 부족으로 어려움을 겪는 대부분의 스핀 안정성 발사체는 공기역학적 힘과 모멘트가 큰 변화를 보이는 음속에 가까운 문제를 가지고 있습니다.총알이 초음속에서 동적 안정성의 상당한 부족을 나타내는 것은 덜 일반적이지만 가능합니다.동적 안정성은 대부분 천음속 공기역학에 의해 결정되기 때문에 발사체가 언제 충분한 동적 안정성을 가질지 예측하기가 매우 어렵습니다(이는 예측하기 가장 어려운 속도(천음속) 영역에서 정확하게 계산하기 어려운 공기역학 계수입니다).동적 안정성을 좌우하는 공기역학적 계수: 피칭 모멘트, 매그너스 모멘트 및 공격의 피치와 각도 동적 모멘트 계수의 합계(예측하기 매우 어려운 양).결국, 총알이 다운 레인지를 가질 동적 안정성의 수준을 정확하게 예측하기 위해 모델링과 시뮬레이션이 할 수 있는 것은 거의 없습니다.발사체의 동적 안정성 수준이 매우 높거나 낮을 경우 모델링이 정답을 맞출 수 있습니다.그러나 상황이 경계선(0 또는 2에 가까운 동적 안정성)인 경우에는 올바른 답을 도출하기 위해 모델링을 사용할 수 없습니다.이것은 현장에서 테스트되고 신중하게 문서화되어야 하는 것들 중 하나입니다.
- ^ G1, G7 및 도플러 레이더 테스트는 QuickTARGET Unlimited, Lapua Edition으로 계산한 드래그 계수(Cd) 예측 방법 예측을 도출했습니다.기울기 상수 인자가 0.5 기본값으로 설정된 렉스 탈러스 코퍼레이션 페이자 기반 탄도 소프트웨어로 계산된 페이자 예측.6 Android용 Lapua Ballistics 1.0 앱으로 계산한 DoF 모델링 예측
- ^ C 데이터는d 엔지니어들이 알려진 수학적 탄도 모델과 특정 표 형식의 데이터를 동시에 테스트하여 실제 비행 행동에 매우 가까운 예측을 얻는 알고리즘을 만드는 데 사용됩니다.
- ^ Wayback Machine 웹 사이트의 Spinershide Archived 2007-11-07은 유효 범위를 다음과 같이 정의합니다.유능하고 훈련된 개인이 총기를 사용하는 범위는 60%에서 80%의 시간 동안 목표물을 명중시킬 수 있는 능력을 가지고 있습니다.실제로, 대부분의 총기는 이보다 훨씬 더 큰 범위를 가지고 있지만 유효 범위보다 더 큰 범위에서 목표물을 명중시킬 가능성은 낮습니다.다양한 총기의 유효 사거리에 대한 좋은 공식은 없는 것 같습니다.
- ^ 장거리 사격 선수가 정확한 탄도 솔루션을 계산하기 위해 조준 매개 변수를 얼마나 정확하게 설정해야 하는지에 대한 예는 이러한 테스트 사격 결과로 설명됩니다.300 m에서 목격된 .338 Lapua Magnum 소총은 측정된 총구 속도 905 m/s에서 250 grain (16.2 g)의 Lapua Scenar 총알을 쏘았습니다.시험 촬영 시 공기 밀도 θ는 1.2588 kg/m³였습니다.테스트 라이플은 1400m에서 인간 몸통 크기의 표적 데드 센터를 타격하기 위해 위도 61도에서 300m 제로 범위에서 13.2m(45.38 MOA)의 상승 보정이 필요했습니다.탄도 곡선 플롯은 1392m와 1408m 사이의 총알이 60cm (2ft) 높이의 목표물에 맞았을 것이라는 것을 보여주었습니다.즉, 0.6%의 범위 오차만 발생했다면 1400m에서 60cm 높이의 목표물을 완전히 놓쳤을 것입니다.동일한 목표물이 덜 도전적인 1000m 거리에서 설정되면 987m와 1013m 사이에 명중할 수 있으며, 이는 1.3%의 범위 오차가 0.338 Lapua Magnum 저격수 라운드로 2 MOA 높이 목표물을 명중시킬 수 있음을 의미합니다.이는 거리가 증가함에 따라 명백하게 사소한 측정 및 판단 오류가 주요 문제가 된다는 것을 명확하게 합니다.
레퍼런스
- ^ 발사체 비행 특성 제어를 위한 설계, AMCP 706-242, 미국 육군 재료 사령부, 1966
- ^ Army (February 1965), Interior Ballistics of Guns (PDF), Engineering Design Handbook: Ballistics Series, United States Army Materiel Command, pp. 1–2, AMCP 706-150, archived from the original (PDF) on January 8, 2016
- ^ "Maximum Point Blank Range and the Battlesight Zero". 30 April 2010. Retrieved 24 December 2022.
- ^ "An Improved Battlesight Zero for the M4 Carbine and M16A2 Rifle". Retrieved 2007-09-11.
- ^ "TM 9-1005-319-10 (2010) - Operator's Manual for Rifle, 5.56 MM, M16A2/M16A3/M4 (Battlesight Zero pages 48-55)" (PDF). Retrieved 2014-06-03.
- ^ "Using a 400 meter zero with 5.45×39". Retrieved 16 November 2014.
- ^ "Prediction of Projectile Performance, Stability, and Free-Flight Motion Using Computational Fluid Dynamics, Weinacht, US Army Research Laboratory, 2003" (PDF). Archived from the original (PDF) on 2021-01-21. Retrieved 2022-06-02.
- ^ "Ballistic Coefficients Do Not Exist!". Retrieved 12 January 2017.
- ^ "Weite Schüsse - drei (German)". Archived from the original on 24 May 2008. Retrieved 24 December 2022.
- ^ "exterior ballistics". Archived from the original on 8 August 2003. Retrieved 12 January 2017.
- ^ "LM Class Bullets, very high BC bullets for windy long Ranges". Archived from the original on 19 February 2008. Retrieved 24 December 2022.
- ^ Litz, Bryan (8 March 2021) [Originally posted 17 June 2009, much extended later]. "A Better Ballistic Coefficient". Archived from the original on 2 August 2009.
- ^ ".338 Lapua Magnum product brochure from Lapua" (PDF). Retrieved 24 December 2022.
- ^ "300 grs Scenar HPBT brochure from Lapua" (PDF). Retrieved 24 December 2022.
- ^ "Ballistic Coefficients - Explained" (PDF). Archived from the original (PDF) on 29 October 2013. Retrieved 12 January 2017.
- ^ "The mathematical modelling of projectile trajectories under the influence of environmental effects, Ryan F. Hooke,∗University of New South Wales Canberra at the Australian Defence Force Academy, 2612, Australia". Archived from the original on 2018-02-04. Retrieved 2018-02-02.
- ^ "Form Factors: A Useful Analysis Tool - Berger Bullets Blog". 16 May 2011. Retrieved 12 January 2017.
- ^ Wayback Machine에서 Art Pejsa 2008-08-29 아카이브 정보
- ^ Pejsa, Arthur. "Pejsa Rifle Ballistics: Art Pejsa's Rifle ballistics software and books". Pejsa Ballistics. Pejsa Ballistics. Archived from the original on 8 February 2012. Retrieved 31 July 2018.
- ^ Arthur J Pejsa (2002). Pejsa's Handbook of New, Precision Ballistics. Kenwood Publishing. p. 3.
- ^ a b Arthur J Pejsa (2008). New Exact Small Arms Ballistics. Kenwood Publishing. pp. 65–76.
- ^ Arthur J Pejsa (2008). New Exact Small Arms Ballistics. Kenwood Publishing. p. 63.
- ^ Arthur J Pejsa (2002). Pejsa's Handbook of New, Precision Ballistics. Kenwood Publishing. p. 34.
- ^ Arthur J Pejsa (2002). Pejsa's Handbook of New, Precision Ballistics. Kenwood Publishing. p. 4.
- ^ Arthur J Pejsa (2008). New Exact Small Arms Ballistics. Kenwood Publishing. pp. 131–134.
- ^ Meijer, Robert. "Pejsa and regular drag functions". Retrieved 12 January 2017.
- ^ Arthur J Pejsa (2008). New Exact Small Arms Ballistics. Kenwood Publishing. pp. 33–35.
- ^ "Test Options & Analysis Techniques:Aerodynamic Coefficients: What's Important & How Can I Measure Them? Jeff Siewert Systems Engineer Arrow Tech Associates, Inc. 2012 NDIA Joint Armaments" (PDF). Archived from the original (PDF) on 2016-12-13. Retrieved 2016-10-15.
- ^ SPIN-73 스피너 컴퓨터 프로그램의 업데이트된 버전, 화이트, 1973.
- ^ 전술 무기를 위한 공기역학적 설계 매뉴얼, NSWC 1981
- ^ 발사체 축대칭 설계를 위한 고체 모델링 개선, 1988
- ^ "Six Degree of Freedom Digital Simulation Model for Unguided Fin-Stabilized Rockets" (PDF). Archived from the original (PDF) on 2017-02-21. Retrieved 24 December 2022.
- ^ "Lapua Ballistics App - Resources - Nammo Lapua". Archived from the original on 20 December 2016. Retrieved 12 January 2017.
- ^ "NABK BASED NEXT GENERATION BALLISTIC TABLE TOOLKIT, Sevsay Aytar Ortac, Umut Durak, Umit Kutluay, Koray Kucuk, Maj. Can Candan, 23RD INTERNATIONAL SYMPOSIUM ON BALLISTICS, TARRAGONA, SPAIN 16-20 APRIL 2007". Retrieved 24 December 2022.
- ^ "BALCO 6/7-DoF Trajectory Model, Pierre Wey, Daniel Corriveau, Thomas A. Saitz, Wim de Ruijter, Peter Strömbäck, 29th International Symposium on Ballistics, Edinburgh, Scotland, May 9‐13, 2016". Retrieved 24 December 2022.
- ^ Corriveau, D. (2017). "Validation of the NATO Armaments Ballistic Kernel for use in small-arms fire control systems". Defence Technology. 13 (3): 188–199. doi:10.1016/j.dt.2017.04.006.
- ^ "A Technical Discussion of the ELD-X™ (Extremely Low Drag – eXpanding) & ELD™ Match (Extremely Low Drag Match) Bullets with Heat Shield™ Tip, Dave Emary, October 2015" (PDF). Archived from the original (PDF) on 2015-11-06. Retrieved 2015-11-01.
- ^ Chuck Hawks. "The 8x50R Lebel (8mm Lebel)".
- ^ 리처드슨 대 미국 대 사건, 72 C.Cl. 51 (1930)
- ^ MC DRG - 발사체의 항력계수 추정을 위한 컴퓨터 프로그램, McCoy, 미 육군 탄도연구소, 1981
- ^ "New Video Series from Applied Ballistics « Daily Bulletin". Archived from the original on 21 October 2016. Retrieved 12 January 2017.
- ^ "The Effect of Boattail Geometry on the Yaw Limit Cycle of Small Caliber Projectiles by Bradley E. Howell Data Matrix Solutions, Aberdeen Proving Ground, MD 21005-5066 and Sidra I. Silton and Paul Weinacht Weapons and Materials Research Directorate, ARL, Aberdeen Proving Ground, MD 21005-5066 27th AIAA Applied Aerodynamics Conference 22 - 25 June 2009, San Antonio, Texas" (PDF). Archived from the original (PDF) on 2016-04-06. Retrieved 2015-01-11.
- ^ "EFFECT OF RIFLING GROOVES ON THE PERFORMANCE OF SMALL-CALIBER AMMUNITION Sidra I. Silton and Paul Weinacht US Army Research Laboratory Aberdeen Proving Ground, MD 21005-5066". Archived from the original on 2015-01-11. Retrieved 24 December 2022.
- ^ "Sandia National Laboratories: News Releases : Sandia's self-guided bullet prototype can hit target a mile away". Archived from the original on 5 February 2012. Retrieved 12 January 2017.
- ^ "Guided .50 Caliber Projectile — DARPA's Steerable Bullet". Retrieved 2020-09-27.
- ^ 코트니, 엘리아, 콜린 모리스, 마이클 코트니. "아마추어 도플러 레이더를 이용한 자유 비행 항력 계수의 정확한 측정" 코넬 대학 도서관 (2016)arXiv:1608.06500
- ^ "Lapua Bullets Drag Coefficient Data for QuickTARGET Unlimited" (PDF). Archived from the original (PDF) on 2010-12-29. Retrieved 24 December 2022.
- ^ "Lapua bullets CD data (zip file)". Retrieved 24 December 2022.
- ^ "Use of Doppler Radar to Generate Trajectory Solutions" (PDF). Archived from the original (PDF) on 2015-09-23. Retrieved 2015-07-22.
- ^ "Hornady® 4DOF Ballistic Calculator Overview". Archived from the original on 2016-08-23. Retrieved 12 January 2017.
- ^ "4DOF Ballistic Calculator". Retrieved 12 January 2017.
- ^ "Drag Variability and the use of the "Axial Form Factor" in the Hornady 4DOF™ Trajectory Calculator" (PDF). Archived from the original (PDF) on 19 October 2016. Retrieved 14 October 2016.
- ^ "Hornady® 4DOF™ (Four Degree of Freedom) Ballistic Calculator Technical Document" (PDF). Archived from the original (PDF) on 2016-10-19. Retrieved 2016-10-14.
- ^ "QuickTARGET Unlimited, Lapua Edition". Archived from the original on 1 July 2012. Retrieved 24 December 2022.
- ^ "Lapua Ballistics freeware exterior ballistic software for mobile phones". Archived from the original on 1 July 2012. Retrieved 24 December 2022.
- ^ "EFFECT OF RIFLING GROOVES ON THE PERFORMANCE OF SMALL-CALIBER AMMUNITION Sidra I. Silton* and Paul Weinacht US Army Research Laboratory Aberdeen Proving Ground, MD 21005-5066". Archived from the original on 2012-10-06. Retrieved 24 December 2022.
- ^ a b 수평 임펄스의 균일한 시퀀스에 의한 공기역학적 점프의 영향 - Gener.쿠퍼, 2004년 7월
- ^ "Understanding Uphill and Downhill Shots in Long Range Shooting: A Primer". backcountrymaven.com. 16 May 2013. Retrieved 28 March 2017.
- ^ William T. McDonald (June 2003). "INCLINED FIRE". Exterior Ballistics.com. Retrieved 12 January 2017.
- ^ Beckstrand, Tom (6 February 2020). "Effects of Rain on Bullet Trajectory". Guns and Ammo. Retrieved 24 December 2022.
- ^ Nenstiel 32°에서 발사된 M80 총알(7.62 x 51 NATO)의 휴식 각도 요
- ^ Nennstiel, Ruprecht. "longr". Retrieved 12 January 2017.
- ^ "Articles - Applied Ballistics LLC". Archived from the original on 7 January 2016. Retrieved 12 January 2017.
- ^ 넨스틸 마그누스 효과
- ^ 넨스티엘 마그누스 포스
- ^ 넨스틸 더 매그너스 모멘트
- ^ "Gyroscopic Drift and Coreolis Acceleration by Bryan Litz". Archived from the original on 2007-11-14. Retrieved 2008-06-24.
- ^ "The Eötvös effect". www.cleonis.nl. Retrieved 24 December 2022.
- ^ Lowrie, William (1997). Fundamentals of Geophysics (illustrated ed.). Cambridge University Press. p. 45. ISBN 0-521-46728-4. 45페이지 발췌
- ^ 미국 육군 연구소는 1999년에 여러 저격 무기 시스템과 다양한 사격 통제 방법의 실질적인 한계에 대한 연구를 수행했습니다.저격 무기 사격 통제 오류 예산 분석 - 레이먼드 본 왈데, 데니스 메츠, 1999년 8월
외부 링크
일반적인 외부 탄도학
- Tan, A.; Frick, C.H. & Castillo, O. (1987). "The fly ball trajectory: An older approach revisited". American Journal of Physics. 55 (1): 37. Bibcode:1987AmJPh..55...37T. doi:10.1119/1.14968. (속도의 제곱에 비례하는 항력하에서 발사체의 운동 계산 단순화)
- "The Perfect Basketball Shot" (PDF). (PDF). Archived from the original (PDF) on March 5, 2006. Retrieved September 26, 2005. 농구 탄도학
소형 암 외부 탄도
- 볼 탄도 계산 소프트웨어
- 총알은 어떻게 날까요? 독일 비스바덴의 루프레히트 넨슈티엘의 작품입니다.
- 외부 Ballistics.com 기사 웨이백 머신에서 2013-03-06 보관
- 외부 탄도학의 단기 과정
- 브라이언 리츠의 장거리 총격에 관한 기사
- 확률론적 무기 고용 구역(WEZ) 분석 2015-09-23 웨이백 머신에서 보관된 브라이언 리츠의 개념 개요.
- Weite Schüse - part 4, 루츠 뮐러의 페이자 모델에 대한 기본 설명(독일어)
- 파타고니아 탄도 탄도학 수학 소프트웨어 엔진
- JBM 소형 무기 탄도 및 온라인 탄도 계산기
- 바이슨 탄도학 포인트 매스 온라인 탄도학 계산기 2011-05-15 웨이백 머신에서 보관.
- 소구경 탄약 공기역학적 특성화를 위한 가상 풍동 실험 - Paul Weinacht 미 육군 연구소 애버딘 증명 그라운드, MD
포병대 외부 탄도학
- 영국 포병 사격 통제 - 탄도 및 데이터
- 야포, 제6권, 탄도 및 탄약
- 엘리자베스 R의 BRL 조사 번호 1371번 대포 포병을 위한 사격표 생산.디킨슨, 1967년 11월 미국 육군 재료 사령부 탄도 연구소
- NABK(NATO 무장 탄도 커널) 기반 차세대 탄도 테이블 Takit, 2007년 4월 16일-20일 스페인 타라고나, 탄도학에 관한 제23회 국제 심포지엄.
- 점화 테이블에서 드래그 함수를 추론할 수 있는 C++의 궤적 계산기
프리웨어 소형 암 외부 탄도 소프트웨어
- Hawke X-ACT Pro FREE 탄도학 앱. iOS, Android, OSX & Windows.
- 체어건 프로 림파이어 및 펠릿건에 대한 탄도학 자유.
- Ballistic_XLR. (MS Excel 스프레드시트)] - Pejsa 스프레드시트의 대폭적인 개선 및 수정(아래).
- GEBC(GNU External Ballistics Computer) - Windows, Linux 및 Mac용 오픈 소스 3DOF 탄도 컴퓨터 - G1, G2, G5, G6, G7 및 G8 드래그 모델을 지원합니다.데릭 예이츠가 만들고 관리했습니다.
- 6mmbr.com 탄도학 섹션은 4개의 프리웨어 외부 탄도학 컴퓨터 프로그램을 호스팅합니다.
- 2DOF & 3DOF R.L. McCoy - Gavre 외장 탄도학(zip 파일) - G1, G2, G5, G6, G7, G8, GS, GL, GI, GB 및 RA4 드래그 모델 지원
- PointBlank Ballistics (zip 파일) - Siacci/Mayevski G1 드래그 모델.
- 레밍턴 슛!레밍턴 공장 탄약용 탄도 계산기(핀소프트의 Shoot! 소프트웨어 기반).Siacci/Mayevski G1 드래그 모델.
- JBM의 소형 무기 탄도 계산기 온라인 궤적 계산기 - G1, G2, G5, G6, G7(일부 발사체의 경우 실험적으로 측정된 G7 탄도 계수), G8, GI, GL 및 일부 발사체의 경우 도플러 레이더 테스트 파생(Cd) 드래그 [1]모델을 지원합니다.
- Pejsa Ballistics (MS Excel 스프레드시트) - Pejsa 모델
- 샤프슈터 프렌드 (Palm PDA 소프트웨어) - 페쟈 모델
- QuickTarget Unlimited, Lapua Edition - QuickTarget Unlimited 탄도 소프트웨어 버전(다운로드하려면 무료 등록 필요) - G1, G2, G5, G6, G7, G8, GL, GS Sphere 9/16" 지원SAAMI, GS Sphere Don Miller, RA4, 소련 1943, 영국 1909 Hatches Notebook 및 일부 Lapua 발사체 도플러 레이더 테스트 파생(Cd) 드래그 모델.
- Java 또는 Android 휴대 전화용 Lapua Ballistics 외부 탄도 소프트웨어.라푸아 발사체 및 카트리지에 대한 도플러 레이더 테스트 파생(Cd) 드래그 모델을 기반으로 합니다.
- 안드로이드 및 iOS용 라푸아 총알로 제한된 라푸아 탄도학 앱 6 DoF 모델.
- BfX - MS Excel 애드인 기능의 Excel 세트에 대한 탄도 - G1, G2, G5, G6, G7 G8 및 RA4 및 Pejsa 드래그 모델과 공기 소총 펠릿용 모델을 지원합니다.사용자 제공 모델(예: Lapua 발사체 도플러 레이더 테스트 파생 모델(Cd))을 처리할 수 있습니다.
- 건심 "건심" 윈도우와 맥용 무료 브라우저 기반 탄도 시뮬레이터 프로그램.
- Windows용 탄도 시뮬레이터 "Ballistic Simulator" 무료 탄도 시뮬레이터 프로그램.
- 5H0T 데이터 내보내기 기능과 차트 작성 기능이 있는 무료 온라인 웹 기반 탄도 계산기.
- SAKO 탄도학은 SAKO에 의해 웨이백 머신 프리 온라인 탄도 계산 장난감에서 2016-03-15 보관되었습니다.계산기는 "SAKO 탄도학" 이름으로 안드로이드 앱(mybeon iOS도, 나는 모릅니다)으로도 사용할 수 있습니다.
- ^ "JBM Bullet Library". Archived from the original on 3 May 2010. Retrieved 24 December 2022.