빌린스키 12면체
Bilinski dodecahedron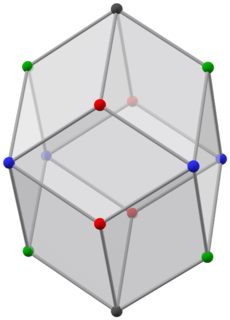 (애니메이션) | |||
| |||
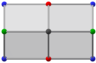
 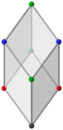 평행한 직교 투영 반대쪽 가장자리 2개, 각각 다음 구성 요소: 검정과 빨강의 정점 / 검정과 초록의 정점 금색 마름모 면의 직교 투영도 | |||
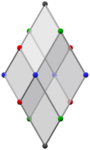  평행한 직교 투영: 4개의 면, 각각 4개의 정점이 있습니다/ 2개의 엣지(각 엣지에는 검은색과 파란색의 정점이 있음) | |||
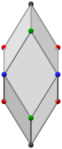
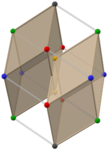 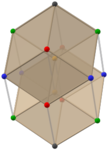 황금 마름모꼴 쌍 (애니메이션) |
기하학에서, 빌린스키 십이면체는 12개의 합동 금색 마름모꼴 면을 가진 볼록한 다면체이다.그것은 면추이 마름모꼴 12면체와 같은 위상을 가지고 있지만 다른 기하학적 구조를 가지고 있다.그것은 조면체이다.
역사
이 모양은 1752년 존 [1][2]로지 카울리가 쓴 도데카롬부스라는 책에 등장한다.그것은 1960년에 [3]그것을 재발견한 Stanko Bilinski의 이름을 따서 명명되었다.빌린스키 자신은 그것을 [4]두 번째 종류의 마름모꼴 12면체라고 불렀다.빌린스키의 발견은 에브그라프 페도로프의 합동 마름모꼴 [5]볼록 다면체 분류에서 75세의 누락 사항을 수정했다.
정의 및 속성
| 도 | 색. | 좌표 | |
|---|---|---|---|
| 3 | 빨간. | (0, ±1, ±1) |  |
| 초록의 | (±120, 0, ±120) | ||
| 4 | 파랑색 | (±120, ±1, 0) | |
| 블랙입니다. | (0, 0, ±1202) | ||
빌린스키 12면체는 12개의 황금 마름모꼴을 접착하여 형성된다.대각선이 황금비인 마름모꼴입니다.결과 다면체의 그래프는 마름모꼴 12면체의 그래프와 동일하지만, 면은 다른 방향을 가지고 있습니다. 반대쪽 마름모꼴의 한 쌍은 마름모꼴 12면체에서 대응하는 마름모꼴의 방향과 비교하여 길고 짧은 대각선이 반대입니다.이러한 반전 때문에 빌린스키 12면체는 대칭의 차수가 낮다.마름모꼴 12면체처럼, 빌린스키 12면체는 3도 정점 8개와 4도 정점 6개를 가지고 있다.그러나 대칭이 다르기 때문에, 그것은 4가지 종류의 정점을 가지고 있습니다: "수직" 축에 있는 두 개의 정점과 각 축 평면에 있는 네 개의 정점(모두 "수평" 축 평면에 있는 네 개의 정점, 두 개의 "수직" 축 평면에 있는 여섯 개의 정점).그것의 면은 세 가지 다른 종류의 합치된 12개의 금색 마름모꼴이다: 두 개는 파란색과 녹색의 정점이 번갈아 있는 두 개, 그리고 여덟 개는 네 개의 정점이 모두 있다.
이 솔리드의 대칭군은 직사각형 입방체의 대칭군 D와 동일합니다2h.8면체 대칭의 부분군이며, 8개의 요소가 있습니다: 2중 대칭의 세 축, 세 개의 대칭 평면(이 고체의 축 평면이기도 함), 그리고 대칭의 중심(2가 짝수이기 때문에)입니다.
그것은 평행면체이며, 따라서 공간을 채우는 다면체이기도 하다.
마름모꼴 12면체와의 관계
1962년 [6]논문에서 H. S. M. 콕서터는 빌린스키 12면체는 마름모꼴 12면체에서 아핀 변환을 통해 얻을 수 있다고 주장했지만 이는 거짓이다.빌린스키 12면체에서 긴 본체 대각선은 두 면의 짧은 대각선과 평행하고 다른 두 면의 긴 대각선은 평행하기 때문이다.마름모꼴 12면체에서 대응하는 본체 대각선은 네 개의 짧은 면 대각선에 평행하며, 마름모꼴 12면체의 아핀 변환에서 이 본체 대각선은 네 개의 같은 길이 면 대각선에 평행하게 유지될 것이다.두 십이면체의 또 다른 차이점은 마름모꼴 12면체에서 반대쪽 도-4 정점을 연결하는 모든 체 대각선이 대각선과 평행한 반면, 빌린스키 12면체에서 이 유형의 짧은 체 대각선은 평행한 면 [5]대각선이 없다는 것이다.
관련 조노헤드라
빌린스키 12면체는 평행한 모서리를 가진 10개의 금색 마름모꼴 면과 8개의 금색 마름모꼴 면의 두 개의 구역이나 벨트를 제거하거나 붕괴시킴으로써 마름모꼴 3면체(또 다른 금색 마름모꼴 면)로부터 형성될 수 있다.10개의 면으로 이루어진 하나의 구역만 제거하면 마름모꼴 20면체가 생성됩니다.10면, 8면, 6면 3개의 구역을 제거하면 황금색 [4][5]마름모꼴이 됩니다.따라서, 빌린스키 12면체에서 6개의 면으로 이루어진 영역을 제거하면 황금색 마름모 면이 만들어집니다.빌린스키 12면체는 4개의 황금색 마름모꼴로 해부할 수 있으며,[7] 각 유형별로 2개씩이다.
이러한 조노헤드라의 정점은 3에서 6개의 벡터의 선형 조합으로 계산할 수 있습니다.벨트n m은 n개의 방향 벡터를 나타내며 (최대) m개의 코파라렐 합치 에지를 포함하는 벨트를 의미한다.빌린스키 12면체에는 6개의 코팔렐 모서리의 벨트 4개가 있습니다.
이 조노헤드라(zonoheadra)는 n차원 투영 기준으로 황금비 of의 하이퍼큐브의 투영 봉투입니다.n=6의 구체적인 근거는 다음과 같다.
- x = (1, φ, 0, -1, φ, 0)
- y = (표준, 0, 1, 0, -1)
- z = (0, 1, θ, 0, -1, θ)
n=5의 경우 여섯 번째 열을 제거한 경우에도 기준이 같습니다.n=4의 경우 5번째 및 6번째 열이 제거됩니다.
| 솔리드 네임 | 삼면체 | 이십면체 | 십이면체 | 육면체 | 마름모꼴 |
|---|---|---|---|---|---|
| 가득한 대칭 | 나h 주문 120 | D5d. 주문 20 | D2h. 오더 8 | D3d. 주문 12 | 디2 주문 4 |
| (2(n-1))n 벨트 | 10개6 | 8개5 | 6개4 | 4개3 | 2개2 |
| n(n-1) 얼굴 | 30 | 20 (−10) | 12 (−8) | 6 (−6) | 2 (−4) |
| 2n(n-1) 가장자리 | 60 | 40 (−20) | 24 (−16) | 12 (−12) | 4 (−8) |
| n(n-1)+2 꼭지점 | 32 | 22 (−10) | 14 (−8) | 8 (−6) | 4 (−4) |
| 솔리드 이미지 |  |  | 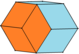 |  | |
| 평행 모서리 이미지 |  |  | |||
| 절개요 | 10 | 5 | 2 | ||
| 투사적 폴리토프 | 6큐브 | 5큐브 | 4큐브 | 3큐브 | 2큐브 |
| 투사적 n입방체 이미지 |  |  |  |
레퍼런스
- ^ 를 클릭합니다Hart, George W. (2000), "A color-matching dissection of the rhombic enneacontahedron", Symmetry: Culture and Science, 11 (1–4): 183–199, MR 2001417.
- ^ Hart(2000)가 인용한 바와 같이Cowley, John Lodge (1752), Geometry Made Easy; Or, a New and Methodical Explanation of the Elements of Geometry, London, Plate 5, Fig. 16.
- ^ 를 클릭합니다Bilinski, S. (1960), "Über die Rhombenisoeder", Glasnik Mat. Fiz. Astr., 15: 251–263, Zbl 0099.15506.
- ^ a b 를 클릭합니다Cromwell, Peter R. (1997), Polyhedra: One of the most charming chapters of geometry, Cambridge: Cambridge University Press, p. 156, ISBN 0-521-55432-2, MR 1458063.
- ^ a b c 를 클릭합니다Grünbaum, Branko (2010), "The Bilinski dodecahedron and assorted parallelohedra, zonohedra, monohedra, isozonohedra, and otherhedra", The Mathematical Intelligencer, 32 (4): 5–15, doi:10.1007/s00283-010-9138-7, hdl:1773/15593, MR 2747698.
- ^ Coxeter, H. S. M. (1962), "The classification of zonohedra by means of projective diagrams", Journal de Mathématiques Pures et Appliquées, 41: 137–156, MR 0141004. (기하학의 아름다움)에 전재. 12편의 에세이, 도버, 1999, MR1717154)
- ^ "Golden Rhombohedra", CutOutFoldUp, retrieved 2016-05-26
외부 링크
- VRML 모델 George W. Hart : www.georgehart.com/virtual-polyhedra/vrml/rhombic_dodecahedron_of_second_kind.wrl
- 애니메이션과 좌표, 데이비드 1세McCoey: dmccooey.com/polyhedra/BilinskiDodecahedron.html
- 크로아티아에서 온 새로운 마름모꼴 12면체! Matt Parker의 YouTube 동영상