월시도

Walsh diagram
월시 HAH 분자의 다이어그램.

종종 각도 좌표 다이어그램 또는 상관 다이어그램이라고 불리는 월시 다이어그램은 분자의 계산된 궤도 결합 에너지 대 왜곡 좌표(결합 각도)의 표현으로, 작은 [1][2]분자의 기하학적 구조에 대한 빠른 예측을 위해 사용됩니다.기하학적 변화의 함수로서 분자의 분자 궤도 수준의 변화를 그림으로 표시함으로써, 월시 다이어그램은 분자가 왜 특정한 공간 구성에서 더 안정적인지 설명한다(예를 들어 왜 물이 구부러진 구조를 [3]채택하는지).

월시 다이어그램의 주요 적용은 동일한 수의 원자가 전자를 가진 관련 분자에 대해 관찰된 구조의 규칙성을 설명하고(예를 들어 HO와2 HS가 유사해 보이는 이유2), 분자가 전자 수 또는 스핀 상태의 변화에 따라 기하학적 구조를 어떻게 변화시키는지를 설명하는 것이다.또한 월시 다이어그램은 분자가 기하학적 섭동을 겪을 때 LUMO(최저 점유 분자 궤도)가 HOMO(최고 점유 분자 궤도)에 어떻게 영향을 미치는지에 대한 지식으로부터 분자 기하학의 왜곡을 예측하는 데 사용될 수 있다.

분자의 모양을 예측하는 월시의 법칙은 분자가 호모에게 가장 안정감을 주는 구조를 채택할 것이라고 말한다. 만약 특정한 구조적 변화가 호모를 교란시키지 않는다면, 가장 가까운 점유된 분자 궤도는 기하학적 [4]방향에 대한 선호도를 지배한다.

역사

월시 도표는 A.D.에 의해 처음 도입되었다. 던디 대학의 영국 화학 교수인 월시는 화학 [5][6][7][8][9][10][11][12][13][14]학회 저널의 한 호에서 10개의 논문을 연재했다.여기서, 그는 Mulliken의 이론적 공헌을 적용하여 바닥 상태와 들뜬 상태의 다원자 분자에 의해 채택된 형태를 합리화하는 것을 목표로 했다.구체적으로, 월시는 분자 모양의 변화가 분자 궤도의 에너지에 미치는 영향을 계산하고 설명했습니다.월시 도표는 그러한 의존성의 예시이며, 그의 결론은 "월시 [15]규칙"이라고 언급된다.

그의 출판물에서, Walsh는 여러 가지 예를 통해 기저 상태의 분자에 의해 채택된 기하학이 주로 원자가 [16]전자의 수에 의존한다는 것을 보여주었다.그 자신은 이 일반적인 개념이 참신하지 않다는 것을 인정했지만, 그가 이용할 수 있는 새로운 데이터가 이전의 일반화를 확장하고 연마할 수 있게 해주었다고 설명했다.그는 또한 멀리켄이 이전에 두 개의 다른 핵 구성에서 다원자 분자의 가능한 궤도에 대한 상관도를 구축하려고 시도했고, 심지어 이 도표를 그들의 지면과 들뜬 상태의 [17][18]분자의 모양과 스펙트럼을 설명하기 위해 사용하려고 시도했다고 언급했다.그러나 멀리켄은 각도의 증가로 특정 곡선의 상승과 하강 이유를 설명할 수 없었고, 따라서 월시는 "그의 도표는 경험적이거나 발표되지 않은 [5]계산에 기초했다"고 주장했다.

개요

월시는 원래 그가 "궤도 결합 에너지" 대 결합 각도라고 묘사한 것을 그림으로 그려서 그의 도표를 구성했다.Walsh가 실제로 이 용어로 설명했던 것은 불분명하다; 어떤 사람들은 그가 실제로 이온화 잠재력을 언급했다고 믿지만,[19] 이것은 여전히 논쟁의 주제이다.어쨌든, 그가 제시한 일반적인 개념은 분자의 총 에너지는 그 분자에 있는 모든 "궤도 결합 에너지"의 합과 같다는 것이었다.따라서 분자결합각의 변화에 의한 각 오비탈의 안정화 또는 불안정화에 관한 지식으로부터 분자의 특정 상태에 대한 평형결합각을 예측할 수 있다.하나의 구성을 안정시키기 위해 상호 작용하는 궤도(예:Linear)는 다른 구성(예: 중복되지 않을 수 있습니다.구부러짐)을 통해 한 지오메트리가 다른 지오메트리에 비해 계산상 안정적입니다.

일반적으로 코어 궤도(B, C, N, O, F, Ne의 경우 1s)는 에너지가 너무 낮아서 결합 각도의 변화에 의한 유의한 변화를 경험하지 않기 때문에 월시 다이어그램에서 제외된다.원자가 궤도만 고려된다.그러나 원자가 궤도의 일부는 종종 비어 있다는 것을 명심해야 한다.

Walsh 다이어그램 생성

월시 도표를 작성할 때, 분자의 기하학적 구조는 먼저 Hartree-를 사용하여 최적화되어야 한다.양자 다체계의 [20]지반 상태 파동 함수와 지반 상태 에너지를 근사하기 위한 폭(HF) 방법[2].다음으로 상기 결정된 평형 형상으로부터 변위된 일련의 형상에 대해 단일점 에너지가 실행된다.단일점 에너지(SPEs)는 분자 내 원자의 특정 배열에 대한 분자의 위치 에너지 표면의 계산입니다.이러한 계산을 수행할 때 결합 길이는 일정하게 유지되며(평형 값에서) 결합 각도만 평형 값에서 변경되어야 한다.그런 다음 각 형상에 대한 단일점 연산을 결합 각도에 대해 플롯하여 대표적인 월시 다이어그램을 생성할 수 있습니다.

월시 다이어그램의 구조

AH 분자에2 대한 월시 다이어그램(예2: HO)

AH2 분자

가장 단순한2 AH 분자 시스템의 경우, Walsh는 결합 각도를 90°에서 180°로 변경하면서 표준 분자 궤도에 대한 ab initio 궤도 에너지 곡선을 그려서 첫 번째 각도 상관도를 생성했다.결합 각도가 왜곡되면 각 궤도에 대한 에너지가 선을 따라 따라 따라갈 수 있으므로 배향 함수로서의 분자 에너지가 빠르게 근사할 수 있습니다.월시 좌표가 핵 격퇴를 고려하는지는 아직 불분명하며,[21] 이는 여전히 논쟁의 주제이다.물의 일반적인 예측 결과는 결합각 90°로, 실험 도출값 104°에도 근접하지 않습니다.기껏해야 이 방법은 구부러진 [2]분자와 선형 분자를 구별할 수 있다.

이 개념은 비수소 AB2 및 BAC 분자, HAB 및 HAH 분자, 4원자 수소화물 분자3(AH), 4원자 무수물 분자(AB), HAB2 분자, 아세트알데히드, 5원자 분자(CH3I), 6원자 분자(에틸렌 및 벤젠)를 포함한 다른 종에도 적용될 수 있다.

반응성

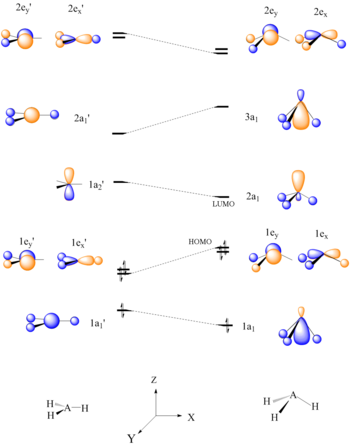
월시 다이어그램은 분자 궤도 이론과 함께 반응성을 예측하는 도구로도 사용될 수 있습니다.월시도를 생성하고 그 분자의 HOMO/LUMO를 결정함으로써 분자가 어떻게 반응할지를 결정할 수 있다.다음 예시는 BH, CH3+ 등의3 AH 분자의3 Lewis 산도를 예측한다.

6개의 전자3 AH 분자는 평면 구조를 가져야 한다.평면3 AH의 HOMO, 1e'는 A-H 결합을 구부려 피라미드 모양을 형성할 때 결합의 파괴에 의해 불안정함을 알 수 있다.하나의 원자 중심에 집중된 LUMO는 좋은 전자 수용체이며 BH와3+ [22]CH의 루이스3 산 특성을 설명한다.

월시 상관도는 상대 분자 궤도 에너지 수준을 예측하는 데도 사용할 수 있다.평면3+ CH에서 사면체 CH-Nu로의3 수소 원자의 왜곡은 C-Nu 결합 궤도 [22]δ의 안정화를 일으킨다.

평면3 AH 분자에 대한 월시 다이어그램
CH에 대한3+ 친핵 첨가에 대한 궤도 상호작용도

기타 상관도

다른 상관도는 다나베 스가노 다이어그램과 오르골 다이어그램이다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ IUPAC, 화학 용어집, 제2판('골드북') (1997).온라인 수정판: (2006–) "상관도".doi:10.1351/goldbook.C01348
  2. ^ a b c Miller Carrie S (2015). "Walsh Diagrams: Molecular Orbital and Structure Computational Chemistry Exercise for Physical Chemistry". Journal of Chemical Education. 92: 1040–1043. doi:10.1021/ed500813d.
  3. ^ Chen, E.; Chang, T. (1998). "Walsh Diagram and the Linear Combination of Bond Orbital Method". Journal of Molecular Structure: THEOCHEM. 431 (1–2): 127–136. doi:10.1016/S0166-1280(97)00432-6.
  4. ^ Mulliken, R.S. (1955). "Structures of the Halogen Molecules and the Strength of Single Bonds". J. Am. Chem. Soc. 77 (4): 884–887. doi:10.1021/ja01609a020.
  5. ^ a b Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part I. AH2 Molecules". J. Chem. Soc.: 2260–2266. doi:10.1039/JR9530002260.
  6. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part II. AB2 and BAC Molecules". J. Chem. Soc.: 2266–2288. doi:10.1039/JR9530002266.
  7. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part III. HAB and HAAH Molecules". J. Chem. Soc.: 2288–2296. doi:10.1039/JR9530002288.
  8. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part IV. Tetratomic hydride molecules, AH3". J. Chem. Soc.: 2296–2301. doi:10.1039/JR9530002296.
  9. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part V. Tetratomic, non-hydride molecules, AB3". J. Chem. Soc.: 2301–2306. doi:10.1039/JR9530002301.
  10. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part VI. H2AB Molecules". J. Chem. Soc.: 2306–2317. doi:10.1039/JR9530002306.
  11. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part VII. A note on the near-ultra-violet spectrum of acetaldehyde". J. Chem. Soc.: 2318–2320. doi:10.1039/JR9530002318.
  12. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part VIII. Pentatomic molecules: CH3I Molecules". J. Chem. Soc.: 2321–2324. doi:10.1039/JR9530002321.
  13. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part IX. Hexatomic molecules: ethylene". J. Chem. Soc.: 2325–2329. doi:10.1039/JR9530002325.
  14. ^ Walsh, A.D. (1953). "The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part X. A note on the spectrum of benzene". J. Chem. Soc.: 2330–2331. doi:10.1039/JR9530002330.
  15. ^ Mulliken, R.S. (1955). "Bond Angles in Water-Type and Ammonia-Type Molecules and Their Derivatives". J. Am. Chem. Soc. 77 (4): 887–891. doi:10.1021/ja01609a021.
  16. ^ Walsh, A.D. (1976). "Some Notes on the Electronic Spectra of Small Polyatomic Molecules". Int. Rev. Sci.: Phys. Chem. Series 2. 3: 301–316.
  17. ^ O'Leary, B.; Mallion, R.B. (1987). "Walsh Diagrams and the Hellman-Feynman Theorem: A Tribute to the Late Professor Charles A. Coulson, F.R.S. (1910-1974)". Journal of Mathematical Chemistry. 1 (4): 335–344. doi:10.1007/BF01205066.
  18. ^ Atkins, P.W. (1970). Molecular Quantum Mechanics. Oxford, Massachusetts: Clarendon Press. ISBN 978-0-19-855129-4.
  19. ^ Peters, D. (1966). "Nature of the One-Electron Energies of the Independent Electron Molecular Orbital Theoryand the Walsh Diagrams". Transactions of the Faraday Society. 6: 1353–1361.
  20. ^ Chen, E.; Chang, T. (1997). "Orbital Interaction and the Mulliken-Walsh Diagram for AH2 Systems". Journal of the Chinese Chemical Society (Taipei). 44: 559–565. doi:10.1002/jccs.199700086.
  21. ^ Takahata, Y.; Parr, R.G. (1974). "Three Methods to Look at Walsh-type Diagrams Including Nuclear Repulsions". Bulletin of the Chemical Society of Japan. 47 (6): 1380–1386. doi:10.1246/bcsj.47.1380.
  22. ^ a b Atkins, P.W..; et al. (1970). Inorganic Chemistry: Shriver and Atkins. Oxford, U.K.: Oxford University Press. ISBN 978-0-19-926463-6.

외부 링크