유형 2 퍼지 세트 및 시스템

Type-2 fuzzy sets and systems

형식 2 퍼지 집합과 시스템은 더 많은 불확실성을 처리할 수 있도록 표준 형식 1 퍼지 집합과 시스템을 일반화한다. 퍼지 집합의 시작부터, 타입 1 퍼지 집합의 멤버쉽 함수가 그것과 관련된 불확실성을 가지고 있지 않다는 사실에 대한 비판은, 그 단어가 많은 불확실성의 함축성을 가지고 있기 때문에 퍼지라는 단어와 모순되는 것처럼 보이는 어떤 것에 대해 이루어졌다. 그렇다면 멤버십 함수의 가치에 대한 불확실성이 있을 때 무엇을 하는가? 이 질문에 대한 답은 1975년 퍼지 집합의 발명자인 로트피 A. 자데가 더 정교한 종류의 퍼지 집합을 제안했을 때 제공되었는데,[1] 그 중 첫 번째 것은 "타입-2 퍼지 집합"이라고 불렀다. 타입 2 퍼지 집합은 퍼지 집합 이론에 멤버쉽 함수에 대한 불확실성을 포함시킬 수 있도록 하며, 타입 1 퍼지 집합에 대한 위의 비판을 정면으로 다루는 방법이다. 그리고 불확실성이 없는 경우, 타입 2 퍼지 집합은 타입 1 퍼지 집합으로 감소하며, 이는 예측 불가능성이 사라질 때 결정론에 대한 확률을 감소시키는 것과 유사하다.

제1형 퍼지 시스템은 고정된 멤버십 함수로 작동하고 있는 반면 제2형 퍼지 시스템에서는 멤버십 함수가 변동하고 있다. 퍼지 집합은 입력 값을 퍼지 변수로 변환하는 방법을 결정한다.[2]

개요

유형 1 퍼지 집합과 유형 2 퍼지 집합을 상징적으로 구별하기 위해, 길드 기호가 퍼지 집합의 기호 위에 놓인다. 따라서, A는 유형 1 퍼지 집합을 나타내는 반면, ENG는 유사한 유형 2 퍼지 집합을 나타낸다. 후자가 완료되면, 결과적인 타입 2 퍼지 세트를 "일반 타입 2 퍼지 세트"라고 부른다(특수 간격 타입 2 퍼지 세트와 구별하기 위해).

자데는 제2형[1] 퍼지 집합으로 멈추지 않았다. 왜냐하면 1976년 논문에서 그는 또한 이 모든 것을 제2형 퍼지 집합으로 일반화했기 때문이다. 본 논문은 유형 1에서 유형 n 퍼지 집합으로의 논리적 진행의 다음 단계이기 때문에 유형 2 퍼지 집합에만 초점을 맞추고 있다(여기서 n = 1, 2, ...). 일부 연구자들은 유형 2 퍼지 집합보다 높은 것을 탐구하기 시작하고 있지만, 2009년 초 현재, 이 연구는 초기 단계에 있다.

그림 1. 일반 타입 2 퍼지 집합의 멤버십 함수는 3차원이다. 3차원의 한 슬라이스 단면이 표시된다. 이 단면은 다른 모든 단면뿐만 아니라 FOU에 위치한다. 단면의 경계만이 일반 타입 2 퍼지 집합의 멤버쉽 기능을 설명하는데 사용된다. 그것은 예술적인 목적으로 채워져 있는 것으로 보여진다.

일반 타입 2 퍼지 집합인 ENG의 멤버십 함수는 3차원(그림 1)이며, 여기서 세 번째 차원은 그것의 "불확실성의 발자국"(FOU)이라고 불리는 2차원 영역의 각 지점에서 멤버십 함수의 값이다.

간격 형식 2 퍼지 집합의 경우, 3차원 값이 모든 곳에서 동일하다는 (예: 1) 퍼지 집합의 경우, 즉 간격 형식 2 퍼지 집합의 세 번째 차원에는 새로운 정보가 포함되지 않는다는 것을 의미한다. 그래서 그러한 집합의 경우, 3차원은 무시되고, 그것을 기술하는 데 FOU만 사용된다. 이러한 이유로 구간 유형 2 퍼지 세트를 1차 불확도 퍼지 세트 모델이라고도 하는 반면, 일반 유형 2 퍼지 세트(유용한 3차 치수 포함)는 2차 불확도 퍼지 세트 모델이라고도 한다.

그림 2 구간 유형 2 퍼지 집합에 대한 FOU. 많은 다른 모양들이 FOU를 위해 가능하다.

FOU는 제1형 멤버십 함수의 흐릿함을 나타내며, 제1형 퍼지 집합인 두 가지 경계 함수(그림 2), 하부 멤버십 함수(LMF), 상위 멤버십 함수(UMF)로 완전히 설명된다. 따라서 유형 1 퍼지 집합 수학을 사용하여 구간 유형 2 퍼지 집합의 특성을 지정하고 작업할 수 있다. 이것은 유형 1 퍼지 집합을 이미 알고 있는 엔지니어와 과학자들이 구간 유형 2 퍼지 집합을 이해하고 사용하기 위해 일반 유형 2 퍼지 집합 수학에 대해 학습하는 데 많은 시간을 투자하지 않아도 된다는 것을 의미한다.

제2형 퍼지 세트에 대한 연구는 1980년대와 1990년대 초에서 중반에 걸쳐 약화되었지만, 그것에 대한 소수의 기사가 발표되었다. 사람들은 여전히 제1형 퍼지 세트를 어떻게 해야 할지 궁리하고 있었기 때문에, 자데가 1976년에 제2형 퍼지 세트를 제안했음에도 불구하고, 연구자들이 제2형 퍼지 세트에 초점을 맞추기 위해 제1형 퍼지 세트로 무엇을 하고 있는지 떨어뜨릴 시간은 적절하지 않았다. 이것은 1990년대 후반에 제리 멘델과 그의 제자의 제2형 퍼지 세트와 시스템에 대한 연구 결과로 바뀌었다.[3] 그 이후로, 전 세계의 점점 더 많은 연구자들이 제2형 퍼지 세트와 시스템에 관한 기사를 쓰고 있다.

구간 유형-2 퍼지 집합

구간 유형 2 퍼지 집합은 그러한 집합에 필요한 수학(주로 구간 산술)이 일반 유형 2 퍼지 집합에 필요한 수학보다 훨씬 단순하기 때문에 가장 많은 관심을 받았다. 따라서 구간 유형 2 퍼지 집합에 대한 문헌은 큰 반면 일반 유형 2 퍼지 집합에 대한 문헌은 훨씬 더 작다. 두 종류의 퍼지 세트 모두 전 세계의 점점 더 많은 수의 연구자들에 의해 활발하게 연구되고 있으며, 로봇 제어와 같은 다양한 분야에서 성공적인 고용을 가져왔다.[4]

다음 사항에 대한 공식은 간격 유형 2 퍼지 집합에 대해 이미 해결되었다.

구간 유형 2 퍼지 논리 시스템

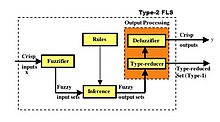
제2형 퍼지 집합은 FLS(규칙 기반 퍼지 논리 시스템)에 매우 광범위한 적용 가능성을 발견하고 있는데, 이는 그러한 불확실성은 제1형 퍼지 집합에 의해 모델링될 수 없는 반면, 그러한 불확실성은 제1형 퍼지 집합에 의해 모델링될 수 없기 때문이다. 형식 2 FLS의 블록 다이어그램은 그림 3에 나와 있다. 이러한 종류의 FLS는 퍼지 논리 제어, 퍼지 논리 신호 처리, 규칙 기반 분류 등에 사용되며, FLS는 오류 함수를 최소화하도록 설계되었기 때문에 퍼지 집합의 함수 근사 적용으로 언급되기도 한다.

그림 3. 2종 FLS

그림 3의 규칙 기반 FLS의 네 가지 구성요소에 대한 다음의 논의는 간격 유형 2 FLS에 대해 주어진다. 지금까지는 그것들이 가장 인기 있는 유형 2 FLS이지만, 대부분의 논의는 일반 유형 2 FLS에도 적용 가능하기 때문이다.

주제 전문가가 제공하거나 수치 데이터에서 추출한 규칙은 IF-DEN 문장의 모음으로 표현된다.

온도가 적당하고 압력이 높을 경우 밸브를 오른쪽으로 약간 돌리십시오.

퍼지 집합은 규칙의 선행 조건(IF-part) 또는 결과(DEN-part)에 나타나는 용어 및 FLS의 입력 및 출력과 연관된다. 멤버십 함수는 이러한 퍼지 집합을 설명하기 위해 사용되며, 타입 1 FLS에서는 모두 타입 1 퍼지 집합인 반면, 간격 형식 2 FLS에서는 적어도 하나의 멤버십 함수가 간격 형식 2 퍼지 집합이다.

간격 유형 2 FLS는 다음과 같은 불확실성 중 하나 또는 모두를 정량화할 수 있다.

  1. 단어들은 다른 사람들에게 다른 것을 의미할 수 있기 때문에, 선행과 규칙의 결과에서 사용되는 단어들.
  2. 불확실한 결과—전문가 그룹으로부터 규칙을 얻었을 때, 결과는 종종 동일한 규칙에 대해 다를 수 있기 때문에, 즉 전문가들이 반드시 동의하는 것은 아니다.
  3. 멤버십 함수 매개변수—이 매개변수가 불확실한 (소음) 훈련 데이터를 사용하여 최적화되면 매개변수가 불확실해지기 때문이다.
  4. 노이즈가 많은 측정—FLS를 활성화하는 것이 매우 빈번하기 때문이다.

그림 3에서 측정된 (크리스프) 입력은 퍼지 집합이기 때문에 퍼지레이터 블록에서 퍼지 집합으로 먼저 변환되며, 숫자가 아니라 퍼지 집합으로 설명되는 규칙을 활성화하는 숫자가 아니기 때문이다. 인터벌 타입 2 FLS에서는 세 가지 종류의 솜털이 가능하다. 측정 시:

  • 완벽해, 바삭바삭한 세트로 모델링.
  • 노이즈가 있지만 노이즈가 정지되어 있으며, 타입 1 퍼지 집합으로 모델링.
  • 노이즈가 많지만 노이즈가 스테이션이 아닌 이들은 간격 유형 2 퍼지 집합으로 모델링된다(이 후자의 유형의 솜털은 타입 1 FLS에서 수행될 수 없다).

그림 3에서, 측정을 솜털로 만든 후, 결과 입력 퍼지 세트는 추론 블록에 의해 퍼지 출력 세트로 매핑된다. 이것은 우선 퍼지 집합 이론을 사용하여 각 규칙을 정량화하고, 그 다음 퍼지 집합의 수학을 사용하여 추론 메커니즘의 도움을 받아 각 규칙의 출력을 설정함으로써 달성된다. M 규칙이 있는 경우, 추론 블록에 대한 퍼지 입력 세트는 그러한 규칙의 하위 집합만 활성화하며, 하위 집합은 적어도 하나의 규칙을 포함하고 일반적으로 M 규칙보다 훨씬 적다. 추론은 한 번에 한 가지 규칙으로 이루어진다. 따라서 추론 블록의 출력에는 하나 이상의 발사 규칙 퍼지 출력 세트가 있을 것이다.

FLS의 대부분의 엔지니어링 애플리케이션에서, 숫자(퍼지 집합은 아님)가 최종 산출물로서 필요하다. 예를 들어, 위에서 주어진 규칙의 결과는 "밸브를 오른쪽으로 약간 회전시킨다"이다. "조금 오른쪽으로"는 언어적 표현이며, 밸브는 반드시 숫자 값, 즉 일정 수의 도에 의해 회전되어야 하기 때문에 어떤 자동 밸브도 이것이 무엇을 의미하는지 알 수 없을 것이다. 따라서, 발사 규칙 출력 퍼지 세트는 숫자로 변환되어야 하며, 이는 그림 3 출력 처리 블록에서 이루어진다.

Type-1 FLS에서, "defuzization"이라고 불리는 출력 처리에서, 타입 1 퍼지 세트를 숫자로 매핑한다. 이를 위한 여러 가지 방법이 있다. 예를 들어, 연소식 규칙 출력 퍼지 집합의 결합(결과는 다른 타입-1 퍼지 집합)을 계산한 다음 해당 집합에 대한 구성원 자격 함수의 무게중심을 계산한다. 연소식 규칙 결과 구성원 자격 함수의 무게중심에 대한 가중 평균을 계산한다.

간격 유형 2 FLS의 경우, 간격 유형 2 퍼지 집합에서 숫자(일반적으로)로 이동하려면 두 단계가 필요하기 때문에 상황은 다소 더 복잡하다(그림 3). "형식 감소"라고 불리는 첫 번째 단계는 구간 유형 2 퍼지 집합이 구간 값 유형 1 퍼지 집합으로 축소되는 것이다. 제1형 탈부착 방법만큼 많은 유형 감소 방법이 있다. 현재 "KM 알고리즘"으로 알려진 Karnik과 Mendel이[6][3] 개발한 알고리즘이 타입 축소를 위해 사용된다. 이 알고리즘은 반복적이지만 매우 빠르다.

유형 감소 후에 발생하는 출력 처리의 두 번째 단계는 여전히 "디퍼지화"라고 불린다. 구간 유형-2 퍼지 집합의 형식 축소 집합은 항상 한정된 번호 구간이기 때문에, 역퍼지화 값은 이 구간에서 두 끝점의 평균에 불과하다.

그림 3에서 보면 구간 유형 2 FLS, 즉 구획 수치 값과 유형 감소 집합에 대한 두 개의 출력이 있을 수 있다는 것이 분명하다. 후자는 선행 조건이나 결과 또는 둘 다 불확실한 규칙을 활성화(가능)한 불확실한 입력 측정으로 인해 간격 형식 2 FLS를 통해 유입된 불확실성의 측정을 제공한다. 표준 편차가 평균 값에 대한 예측 불가능한 불확실성의 측정값을 제공하기 위해 확률과 통계에 널리 사용되는 것처럼, 유형 감소 집합은 구간 유형 2 FLS의 선명한 출력에 대한 불확실성의 측도를 제공할 수 있다.

단어를 사용한 컴퓨팅

퍼지 세트를 위한 또 다른 애플리케이션은 Zadeh[23][24][25] - "Computing with Words"에서 영감을 받았다. "단어를 사용한 컴퓨팅(예: CW 및 CWW)에는 서로 다른 두문자어가 사용되어 왔다. 자데에 따르면:

CWW는 계산의 대상이 자연어에서 도출된 단어와 명제라는 방법론이다. [그것은] 아무런 측정과 계산 없이 매우 다양한 육체적, 정신적 작업을 수행할 수 있는 놀라운 인간의 능력에 의해 영감을 받았다.

물론, 그는 컴퓨터가 숫자보다는 단어나 구를 사용하여 실제로 계산한다는 것을 의미하지는 않았다. 그는 컴퓨터가 단어에 의해 활성화되고, 그것은 퍼지 집합을 사용하여 수학적인 표현으로 변환될 것이며, 이 퍼지 집합은 CWW 엔진에 의해 어떤 다른 퍼지 집합으로 매핑되고, 그 후에 후자는 단어로 다시 변환될 것이라는 것을 의미했다. 당연한 질문은 다음과 같다. 어떤 종류의 퍼지 집합(유형 1 또는 유형 2)을 단어의 모델로 사용해야 하는가? 멘델은[26][27] 칼 포퍼의 "화합주의"[28][25]라는 개념에 근거하여, 타입 1 퍼지 세트를 단어의 모델로 사용하는 것은 과학적으로 옳지 않다고 주장해왔다. 간격 형식 2 퍼지 집합은 단어의 (첫 번째 순서 불확실성) 모델로 사용해야 한다. CWW에 대한 많은 연구가 진행 중이다.

적용들

타입 2 퍼지 세트는 다음과 같은 영역에 적용되었다.

소프트웨어

일반 및 interval type-2 퍼지 세트와 시스템, 타입 1 퍼지 시스템을 다루는 프리웨어 MATLAB 구현은 http://sipi.usc.edu/~puzel/properties에서 이용할 수 있다.
이산 구간 유형 2 퍼지 논리 시스템을 지원하는 소프트웨어는 다음에서 이용할 수 있다.
DIT2FLS 도구 상자 - http://dit2fls.com/projects/dit2fls-toolbox/
DIT2FLS 라이브러리 패키지 - http://dit2fls.com/projects/dit2fls-library-package/

타입-1, interval- 및 일반 타입-2 퍼지 시스템의 소스 코드를 포함한 자바 라이브러리는 http://juzzy.wagnerweb.net/에서 이용할 수 있다.

유형 1 및 유형 2 퍼지 집합에 대한 Python 라이브러리는 https://github.com/carmelgafa/type2fuzzy에서 이용할 수 있다.

interval type 2 퍼지 세트 및 시스템용 Python 라이브러리 https://github.com/Haghrah/PyIT2FLS

Interval Type-2 Puzzy Logic Systems용 오픈 소스 Matlab/Simulink Toolbox는 http://web.itu.edu.tr/kumbasart/type2fuzzy.htm에서 이용할 수 있다.

참고 항목

참조

  1. ^ a b L. A. Zadeh, "언어적 변수의 개념과 근사적 추론–1," 정보 과학, 제8권, 페이지 199–249, 1975.
  2. ^ Jerry Mendel; Hani Hagras; Woei-Wan Tan (16 June 2014). Introduction To Type-2 Fuzzy Logic Control: Theory and Applications. Wiley. ISBN 978-1-118-90144-1.
  3. ^ a b c d e f J. M. 멘델, 불확실한 규칙 기반 퍼지 논리 시스템: 소개와 새로운 방향, 프렌티스 홀, NJ, 2001.
  4. ^ 하산자데, 하미드 레자 등 "3PSP 병렬 로봇에 적용되는 복잡한 동적 시스템에 대한 간격 값 퍼지 컨트롤러." 퍼지 세트 및 시스템 235(2014년): 83-100
  5. ^ N. N. N. Karnik과 J. M. 멘델, "유형-2 퍼지 세트에 대한 운용", 퍼지 세트와 시스템, 제122, 페이지 327–348, 2001.
  6. ^ a b c N. N. N. Karnik과 J. M. 멘델, "타입 2 퍼지 집합의 중심", 정보 과학, 제132권, 페이지 195–220, 2001.
  7. ^ O. Salazar, J. Soriano, H. Serrano, 2012년 5월 콜롬비아 보고타 IEEE 2012 엔지니어링 애플리케이션 워크숍(WEA)에서 "간격 유형 2 퍼지 집합의 중심에 대한 짧은 노트"
  8. ^ D. Wu와 J. M. 멘델, "간격 유형-2 퍼지 집합에 대한 불확실성 조치," 정보 과학, 제177권, 페이지 5378–5393, 2007.
  9. ^ H. Wu와 J. M. 멘델, "불확실성 범위 및 구간 유형-2 퍼지 논리 시스템 설계에서의 용도," IEEE Transs. 2002년 10월 10권 622–639의 퍼지 시스템에 관하여.
  10. ^ H. Bustince, "간격 값 퍼지 집합에 대한 포함 등급 표시자: 구간 값 퍼지 집합에 기초한 근사치 추론 적용" 국제 저널, vol. 23, 페이지 137–209, 2000.
  11. ^ D. Wu와 J. M. 멘델, "간격 유형-2 퍼지 집합과 유형 1 퍼지 집합에 대한 벡터 유사성 측정", 정보 과학, 제 178권, 페이지 381–402, 2008.
  12. ^ a b D. Wu와 J. M. 멘델, "격차 유형-2 퍼지 집합에 대한 순위 결정 방법, 유사성 측정 및 불확실성 측정에 대한 비교 연구," 2009년에 나타날 정보 과학.
  13. ^ J. T. 리카드, J. 아이스벳, G. 기번, D. Morgenthaler, "타입 n 퍼지 집합에 대한 푸지 부분 집합", NAFIPS 2008, 용지 번호 60101, 뉴욕시, 2008년 5월.
  14. ^ O. Salazar와 J. Soriano, "2013년 6월, 캐나다 에드먼턴, 2013년 IFSA World Congress NAFIPS 연례 회의 절차", 페이지 51~56에서 "볼록스 조합을 통해 내장형 1 퍼지 세트를 생성".
  15. ^ O. Salazar 및 J. Soriano, "콘벡스 조합 및 퍼지 집합과 구간 값 퍼지 집합 I에 대한 적용," 응용 수학 과학, 제9권, 제22권, 페이지 1061–1068, 2015.
  16. ^ O. Salazar 및 J. Soriano, "콘벡스 조합 및 퍼지 집합과 구간 값 퍼지 집합 II에 대한 적용," 응용 수학 과학, 제9권, 제22권, 페이지 1069–1076, 2015.
  17. ^ S. -M. 저우, J. M. 가리발디, R. I. 존, F. Chiclana, "영향력 있는 규칙 선택을 통해 파시모니언스 타입 2 퍼지 논리 시스템 구축" IEEE Trans. 퍼지 시스템, 제17권, 제3권, 페이지 654–667, 2009.
  18. ^ M. B. Gorzalczany, "간격 값 퍼지 집합에 기초한 근사 추론 방법," 퍼지 집합과 시스템, 제21권, 페이지 1–17, 1987.
  19. ^ Q. 량·J. M. 멘델, "간격형식-2 퍼지 논리 시스템: 이론과 디자인," IEEE 트랜스. 퍼지 시스템, 제8권, 페이지 535–550, 2000.
  20. ^ F. 류와 J. M. 멘델, "KM 알고리즘에 의해 계산된 퍼지 가중 평균을 사용한 분리," IEEE Trans. 2008년 2월 16일자 1-12면, 퍼지 시스템에 관하여.
  21. ^ D. Wu와 J. M. 멘델, "언어 가중 평균 및 구간 유형-2 퍼지 세트를 사용한 분리," IEEE Trans. 2007년 12월 15권, 페이지 1145–1161의 퍼지 시스템에 대하여.
  22. ^ F. 류와 J. M. 멘델, "간격 접근법을 사용하여 단어를 구간 유형-2 퍼지 집합으로 인코딩" IEEE Trans. 2008년 12월, 16권 페이지 1503–1521, 퍼지 시스템에 대하여.
  23. ^ L. A. Zadeh, "Fuzzy logic = 단어를 사용한 컴퓨팅," IEEE Trans. 퍼지 시스템, 제4권, 페이지 103–111, 1996.
  24. ^ L. A. Zadeh, "숫자가 있는 컴퓨팅에서 단어를 사용한 컴퓨팅까지, 측정 조작에서 인식 조작까지," IEEE Trans. 회로 및 시스템–1, 기본 이론 및 적용, 1999. 4, 페이지 105–119.
  25. ^ a b L. A. Zadeh, "인간 수준의 기계 지능—이것이 달성 가능한가? 새로운 패러다임의 전환의 필요성," IEEE Computing Intelligence Magazine, vol. 3, 페이지 11–22, 2008년 8월.
  26. ^ J. M. 멘델, "Fuzzy Sets for Words: a New Beginning," Proc. IEEE FUZZ 회의, 2003년 5월 26일–28일, 페이지 37–42.
  27. ^ J. M. 멘델, "단어를 사용한 컴퓨터: 자데, 튜링, 포퍼 및 오캄," IEEE Computing Intelligence Magazine, vol. 2, 페이지 10–17, 2007년 11월.
  28. ^ K. Popper, The Logik der Forschung의 번역, 1959년 런던 허친슨.
  29. ^ 카스티요, 오스카 등 "최근 타입 2 퍼지 이미지 처리 애플리케이션 검토" 정보 8.3(2017): 97.
  30. ^ 자란디, MH 파젤 등 "우울증 진단을 위한 일반형 2형 퍼지 전문가 시스템 설계" 응용 소프트 컴퓨팅 80(2019): 329-341.
  31. ^ 디리크, 마흐무트, 오스카 카스티요, 아드난 파티 코카마즈. "간격 유형-2 퍼지 논리 제어를 이용한 시각-서번 기반 글로벌 경로 계획" 공리 8.2 (2019): 58.
  32. ^ 모, 홍, 쉬안밍 자오, 페이유 왕. "무인 차량 시각지침에서 구간형 2 퍼지 집합 적용" 국제 퍼지 시스템즈 저널 21.6 (2019): 1661-1668.
  33. ^ Chai K.C.; Tay K. M.; Lim C.P. (2016). "A perceptual computing-based method to prioritize failure modes in failure mode and effect analysis and its application to edible bird nest farming" (PDF). Applied Soft Computing. 49: 734–747. doi:10.1016/j.asoc.2016.08.043.
  34. ^ 비비, 유수프, 오마르 부할리, 타렉 부크티르. "불확실한 비선형 시스템의 적응적 제어를 위한 페트리 타입 2 퍼지 신경망 근사치." IET 제어 이론 & 애플리케이션 11.17 (2017): 3130-3136.
  35. ^ 타이, 케빈 등 "최근 유형 2 퍼지 컨트롤러 애플리케이션 검토" 알고리즘 9.2 (2016): 39.

외부 링크

이제 IEEE에서 액세스할 수 있는 두 개의 IEEE Expert Now 멀티미디어 모듈이 있다: http://www.ieee.org/web/education/Expert_Now_IEEE/Catalog/AI.html

  • 제리 멘델의 "유형-2 퍼지 세트 및 시스템 소개", IEEE 컴퓨터 인텔리전스 소사이어티 후원
  • "유형 2 퍼지 논리 제어기: IEEE 전산지능학회가 후원하는 하니 하그라스의 '실제 환경 불확실성 대처 방안'에 관한 연구