전환 상태 이론

전환 상태 이론(TST)은 기초 화학 반응의 반응 속도를 설명한다. 이 이론은 반응제와 활성 전이 상태 복합체 사이의 특수한 유형의 화학적 평형(준균형)을 가정한다.^[1]

TST는 주로 화학반응이 어떻게 일어나는지 질적으로 이해하는 데 사용된다. 때문에 절대 반응율의 계산 위치 에너지 surfaces,[2]의 정확한 지식을 필요로 한다 기술 지원 반 덜 절대 반응 속도 상수 계산의 원래 목표에 활성화(ΔH‡, 또한 쓴 Δ‡Hɵ), 활성화(Δ의 표준 엔트로피의 표준 엔탈피를 계산하는데 성공했다 성공적이었다.S‡나 ΔS^‡ɵ), 그리고 속도 상수가 실험적으로 결정된 경우 특정 반응에 대한 활성화의 표준 깁스 에너지(ΔG^‡ 또는 ΔG^‡ɵ)이다. (표기법은 전환 상태에서 관심의 값을 가리키며, ΔH는^‡ 전환 상태의 엔탈피와 반응물질의 엔탈피 사이의 차이를 가리킨다.

이 이론은 1935년 헨리 에이링에 의해, 그 후 프린스턴 대학에서, 그리고 맨체스터 대학의 메러디스 그윈 에반스와 마이클 폴라니에 의해 동시에 개발되었다.^[3][4] TST는 "활성화 복합 이론", "절대율 이론" 그리고 "절대 반응률 이론"^[5]으로도 불린다.

TST가 개발되기 전에는 반응 장벽에 대한 에너지를 결정하기 위해 아르헤니우스 비율 법칙이 널리 사용되었다. 아르헤니우스 방정식은 경험적 관찰에서 파생되며 하나 이상의 반응 매개체가 제품에 대한 반응 물질의 변환에 관여하는지 여부와 같은 기계론적 고려사항을 무시한다.^[6] 따라서 이 법률과 관련된 두 가지 변수인 전우량 인자(A)와 활성화 에너지(E_a)를 이해하기 위해서는 더 많은 개발이 필요했다. Eyring 방정식으로 이어진 TST는 이 두 가지 문제를 성공적으로 해결하지만, 1889년 Arrhenius 비율법(Arrhenius rate law)이 간행된 것과 1935년 TST에서 도출된 Eyring 방정식이 발표된 사이에 46년이 경과했다. 그 기간 동안 많은 과학자들과 연구자들은 이 이론의 발전에 크게 기여했다.

이론

과도기 국가 이론의 이면에 있는 기본 사상은 다음과 같다.

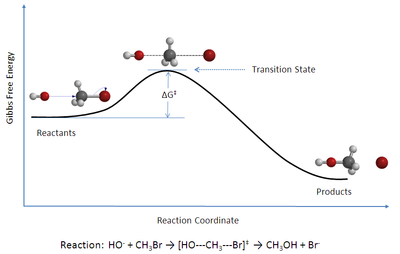
1. 반응 속도는 잠재적 에너지 표면의 안장 지점 근처에 있는 활성화 콤플렉스를 조사함으로써 연구할 수 있다. 이들 단지가 어떻게 형성되는지는 중요하지 않다. 안장점 자체를 전환상태라고 한다.
2. 활성화 콤플렉스는 반응제 분자와 특별한 평형(준균형)에 있다.
3. 활성화된 콤플렉스는 제품으로 전환이 가능하며, 운동이론은 이 변환 속도를 계산하는 데 사용할 수 있다.

개발

TST의 개발에서는 아래와 같이 3가지 접근법을 취하였다.

열역학 처리

1884년 자코쿠스 판 't 호프(Jacobus van 't Hoff)'는 반(Van)'t Hoff 방정식을 제안하여, 가역반응에 대한 평형 상수의 온도 의존성을 기술하였다.

${\displaystyle {\ce {{A}<={B}}}}}$

${\displaystyle {\frac {d\ln K}{d.T}}={\frac {\Delta U}{RT^{2}}:}$

여기서 ΔU는 내부 에너지의 변화, K는 반응의 평형 상수, R은 범용 가스 상수, T는 열역학 온도다. 1889년 스반테 아르헤니우스는 실험적인 작업에 기초하여 다음과 같이 주어진 반작용의 비율 상수에 대해 유사한 표현을 제안하였다.

${\displaystyle {\frac {d\ln k}{d.T}}={\frac {\Delta E}{RT^{2}}:}$

이 표현식의 통합은 아르헤니우스 방정식으로 이어진다.

${\displaystyle k=Ae^{-E_{a}/RT}$

여기서 k는 비율 상수다. A를 주파수 인자(현재 전우량계수라고 하며, E는_a 활성화 에너지로 간주한다. 20세기 초까지 많은 사람들이 아르헤니우스 방정식을 받아들였지만, A와 E에_a 대한 물리적 해석은 모호했다. 이것은 화학적 운동학의 많은 연구자들이 화학적 반응을_a 직접적으로 담당하는 분자 역학과 A와 E를 연관시키려는 시도에서 화학적 반응이 어떻게 일어났는지에 대한 다른 이론을 제시하도록 이끌었다.^{[citation needed]}

1910년 프랑스의 화학자 르네 마르셀린은 활성화의 표준 깁스 에너지의 개념을 도입했다. 그의 관계는 다음과 같이 쓸 수 있다.

${\displaystyle k\propto \exp \exp \left({\frac {-\Delta ^{\dadger }G^{\minus }}}}}}{{\dadgers }}}}}}RT}\오른쪽)}$

마르셀린이 제형을 작업하는 것과 거의 동시에 네덜란드의 화학자 필립 아브라함 콘스탐, 프란스 에포 코넬리스 셰퍼, 위돌드 프란스 브란즈마는 활성화의 표준 엔트로피와 활성화의 표준 엔탈피를 소개했다. 그들은 다음과 같은 비율 상수 방정식을 제안했다.

${\displaystyle k\propto \exp \exp \left({\frac {\delta ^{R}\오른쪽)\exp \expect({\frac {-\Delta ^{}H^{\dadminus }}}}}}}}}{{{\minominus}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}RT}\오른쪽)}$

그러나 상수의 성질은 여전히 불분명했다.

운동이론치료

1900년 초 막스 트라우츠와 윌리엄 루이스는 가스의 운동 이론을 바탕으로 충돌 이론을 이용한 반응 속도를 연구하였다. 충돌 이론은 반응하는 분자들을 서로 충돌하는 단단한 구체로 취급한다; 이 이론은 분자간의 충돌이 완전히 탄력적이라고 가정하기 때문에 엔트로피 변화를 무시한다.

루이스는 다음과 같은 반응에 치료법을 적용하여 실험결과 좋은 합의를 얻었다.

2HI → H₂ + I₂

그러나 나중에 다른 반응에 동일한 치료법을 적용했을 때 이론적 결과와 실험적 결과 사이에 큰 차이가 있었다.

통계기계적 처리

통계 역학은 TST의 발전에 중요한 역할을 했다. 그러나 19세기 중반 제임스 서점 맥스웰, 루드비히 볼츠만, 레오폴드 프펀들러는 분자 운동과 분자 속도의 통계적 분포 측면에서 반응 평형 및 비율을 논하는 여러 논문을 발표했다는 점에서 TST에 대한 통계역학의 적용은 매우 느리게 전개되었다.

프랑스의 화학자 A가 된 것은 1912년이 되어서였다. 베르투드는 요금 상수에 대한 표현을 얻기 위해 맥스웰-볼츠만 분포법을 사용했다.

${\displaystyle {\frac {d\ln k}{d.T}}={\frac {a-bT}{RT^{2}}:}$

여기서 a와 b는 에너지 용어와 관련된 상수다.

2년 후 르네 마르셀린은 화학반응의 진행을 위상공간에서 점의 움직임으로 취급함으로써 본질적인 공헌을 했다. 이어 깁스의 통계-기계적 절차를 적용하고 열역학적 고려에서 앞서 얻은 것과 비슷한 표현을 얻었다.

1915년에, 또 다른 중요한 기여는 영국의 물리학자 제임스 라이스로부터 왔다. 그는 통계적 분석을 토대로 요금 상수가 "중요한 증가율"에 비례한다고 결론 내렸다. 그의 아이디어는 리처드 체이스 톨먼에 의해 더욱 발전되었다. 1919년 오스트리아의 물리학자 카를 페르디난드 헤르츠펠트는 이원자 분자의 가역적 분열을 위해 평형 상수 및 운동 이론에 통계역학을 역반응의 비율 상수인 k에₋₁ 적용하였다.^[7]

${\displaystyle {\ce {AB <=>[k_1][k_{-1}] {A}+{B}}}}}}}}}$

그는 전방 반응의^[8] 속도 상수에 대해 다음과 같은 방정식을 얻었다.

${\displaystyle k_{1}={\frac {k_{\mathrm {B}{}}}{{h}}\좌측(1-e^{-e^{-{\frac {h\nu}{k_{B})T}}}\오른쪽)\exp \left({\frac {-E^{\minus }}}{{\minus }}}}{{RT}\오른쪽)}$

여기서 $E{\displaystyle {}^{}}$ ${\displaystyle {\ominus }^{}}$ ${\$ E$^{\minus }}}$은 절대 영점에서의 분리에너지, k는_B 볼츠만 상수, h는 플랑크 상수, T는 열역학적 온도, $\nu {\displaystyle }$ ${\displaystyle \nu}$은 본드의 진동 주파수다. 이 표현은 TST의 핵심 성분인_B 요인 kT/h가 비율 방정식에 나타난 것은 처음이기 때문에 매우 중요하다.

1920년 미국의 화학자 리처드 체이스 톨먼은 라이스의 결정적인 증대에 대한 생각을 더욱 발전시켰다. 그는 반응의 임계 증가(현재 활성화 에너지라고 함)가 반응을 겪는 모든 분자의 평균 에너지에서 모든 반응 분자의 평균 에너지를 뺀 값과 같다고 결론지었다.

잠재적 에너지 표면

잠재적 에너지 표면의 개념은 TST의 개발에서 매우 중요했다. 이 개념의 토대는 1913년 르네 마르셀린에 의해 세워졌다. 그는 화학반응의 진행은 원자 모멘텀a와 거리에 좌표를 가진 잠재적 에너지 표면의 한 점으로 묘사될 수 있다고 이론화했다.

1931년 헨리 에이링과 마이클 폴라니(Michael Polanyi)는 아래의 반응을 위해 잠재적 에너지 표면을 만들었다. 이 표면은 양자-기계 원리에 기초한 3차원 도표일 뿐 아니라 진동 주파수와 분리의 에너지에 대한 실험 데이터일 뿐이다.

H + H₂ → H₂ + H

에이링과 폴라니 건설 1년 후, 한스 펠저와 유진 위너는 잠재적 에너지 표면에서의 반응의 진행 과정을 따라 함으로써 중요한 공헌을 했다. 이 작업의 중요성은 잠재적 에너지 표면의 col 또는 saddle point라는 개념이 처음으로 논의된 것이었다. 그들은 반응 속도는 그 콜을 통한 시스템의 움직임에 의해 결정된다고 결론지었다.

일반적으로 속도 제한 또는 최저 안장 지점이 초기 지상 상태와 동일한 에너지 표면에 있다고 가정해 왔다. 그러나 최근 반도체와 절연체에서 발생하는 공정에서 초기 흥분 상태가 초기 지상 상태보다 더 낮은 안장 지점을 통과할 수 있다는 사실이 밝혀졌다.^[9]

Eyring 방정식에 대한 정당성

에이링, 폴라니, 에반스가 소개한 가장 중요한 특징 중 하나는 활성화 콤플렉스가 반응물질과 준균형 상태에 있다는 개념이었다. 이 비율은 이러한 단지의 농도에 해당 단지가 제품으로 전환되는 빈도(kT_B/h)를 곱한 것과 정비례한다. 아래에는 Eyring 방정식의 기능적 형태에 대한 비장착성 신뢰성 인수가 제시되어 있다. 그러나 핵심 통계적 기계적 요인 kT_B/h는 정당화되지 않을 것이며, 아래에 제시된 주장은 Eyring 방정식의 진정한 "분열"을 구성하지 않는다.^[10]

준균형 가정

준균형성은 고전적인 화학적 평형과는 다르지만 유사한 열역학적 처리를 사용하여 설명할 수 있다.^{[5] [11]} 아래의 반응을 고려하십시오.

${\displaystyle {\ce {{A}+{B}<=}{[]AB]^{\ddager }->{P}}}}}$

활성화 콤플렉스를 포함한 시스템 내의 모든 종들 간에 완전한 평형을 이루는 경우, [AB].^‡ 통계역학을 이용하여 A와 B의 농도의 관점에서 [AB]^‡의 농도를 계산할 수 있다.

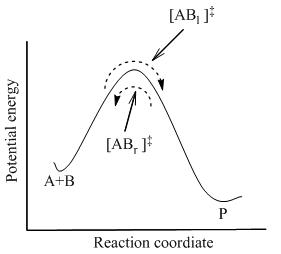
TST는 반응물질과 제품이 서로 평형을 이루지 못할 때에도 활성단지가 반응물질과 준균형 상태에 있다고 가정한다. 그림 2에 나타낸 것처럼, 어느 순간에도 몇 가지 활성화 콤플렉스가 있으며, 어떤 것은 바로 과거에 반응하는 분자로, [AB_l]^‡로 지정되어 있다(좌에서 우로 이동하기 때문에). 나머지는 바로 과거[AB_r]^‡의 제품 분자였다.

TST에서는, 두 방향의 활성화 콤플렉스의 유속이 서로 독립되어 있다고 가정한다. 즉, 모든 제품 분자가 반응 시스템에서 갑자기 제거되면 [AB_r]^‡의 흐름이 멈추지만, 여전히 왼쪽에서 오른쪽으로의 흐름이 있다. 따라서 기술적으로 정확하다면, 반응물질은 바로 이전에 반응물질이었던 활성화 콤플렉스인 ^‡[AB_l]와만 평형을 이룬다.

신뢰성 인수

활성화 콤플렉스는 볼츠만 에너지 분포를 따르지 않지만, "균형 상수"는 그들이 따르는 분배에서 여전히 도출될 수 있다. 준평형평형을 위한 평형 상수 K는^‡ 다음과 같이 쓸 수 있다.

${\displaystyle K^{}}$ ${\displaystyle {‡}^{}}$=${\displaystyle \frac{{}^{}}{}}$[ ${\displaystyle \frac{{\text{AB}}^{}}{}}$ ${\displaystyle \frac{{]}^{}}{}}$‡ [ ${\displaystyle \frac{\text{A}]}{}}$ [ ${\displaystyle \frac{\text{B}}{}}$]$${\$displaystyle$ K$^{\dadager }={\frac${\$ce {[AB]^{\dadager }}}}{\ce {[A][B$

그래서 전환상태 AB의^‡ 화학적 활동은

${\displaystyle [}$ ${\displaystyle \text{AB}}$ ${\displaystyle ]{}^{}}$ = ${\displaystyle {}^{}}$ ${\displaystyle {‡}^{}}$[ ${\displaystyle A}$ ${\displaystyle ]}$[ ${\displaystyle B}$ ${\displaystyle ]}$ ${\displaystyle [{\ce {AB}^{\dadager }=K^{\ce {A}][{\ce {B$

따라서 제품 생산에 대한 비율 방정식은 다음과 같다.

${\displaystyle {\frac {d[{\ce {P}}]}{dt}}=k^{\ddagger }[{\ce {AB}}]^{\ddagger }=k^{\ddagger }K^{\ddagger }[{\ce {A}}][{\ce {B}}]=k[{\ce {A}}][{\ce {B}}]}$,

요율 상수 k가 주어지는 곳

${\displaystyle k}$= ${\displaystyle {}^{}}$ ${\displaystyle {‡}^{}}$ ${\displaystyle {}^{}{}^{}}$ ${\displaystyle {‡}^{}}$ ${\$ $\}\}\}\}.$

여기, k‡ 직접 진동 모드 그 제품에 대한 활성화된 단지 전환할 책임이의 주파수에, 이 진동 방식의 주파수는ν{\displaystyle \nu}. 모든 진동이 반드시 제품의 형성에 비례 상수 κ{\displaystyle \kappa}그래서 이어지지는 않는다, 정비례한다. r이 효과를 설명하기 위해 전송 계수로서 도입된다. 그래서 k는^‡ 로 다시 쓰일 수 있다.

${\displaystyle k^{}}$ ${\displaystyle {‡}^{}}$= ${\displaystyle \kappa }$ ${\displaystyle \nu }$ ${\displaystyle k^{\dadager }=\kappa \nu$$}.$

평형 상수 K의^‡ 경우 통계 역학은 다음과 같이 주어진 온도 의존적 표현으로 이어진다.

${\$$T}{h\nu }}}K^{\ddager '}}}}($${\displaystyle {}^{}{{}^{}}^{}}$‡ ${\displaystyle {{\prime }^{}}^{}{}^{}}$=${\displaystyle {\frac{\mathrm{e}}{}}^{}}$ - ${\displaystyle {\frac{\Delta }{}}^{}}$ G ${\displaystyle {\frac{{‡}^{}}{}}^{}}$ R T ${\$ K$^{\dager '}=e$^{:e$^{\frac{-\delta$G^{\$dager$}}}}}}}}}}}}}{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$RT}}$ ).$$

k와^‡ K의^‡ 새로운 표현을 합치면 새로운 비율 상수 표현을 쓸 수 있는데, 이 표현은 다음과 같이 주어진다.

$\$$T}{h}e^{{h}e^{\frac {-\Delta G^{\dadager}}}}{{}}{{}}}}{{}}}}{$$RT}}=\kappa {\frac {k_{B}$$T}{h}}K^{\ddagger$ $\text{'}\}\}\}\}.$

정의에 따라^‡ ΔG = ΔH^‡ –TΔS는^‡ Eyring 방정식의 대체 형식을 제공하기 위해 비율 상수 식을 확장할 수 있다.

${\$$T}{h}}e^{\frac {\Delta S^{\dadager}}{R}e^{\frac {-\Delta H^{\dagger}}}{{$$R}}}{{R}e^{\dager}}}}{R}}}}}}{\dager}}}}}}{{{$$RT$

정확한 치수성을 위해 방정식은 분자적이지 않은 반응에 대해 (c^⊖)^1–m의 추가 인자를 가져야 한다.

${\$$T}{{h}e^{\frac{\Delta$ S$^{\dadager}}{R}e^{{R}{-\Delta H^{\dadager}}}}{RT}}(c^{\minus }}}}}}}}{1-m$

여기서 c는^⊖ 표준 농도 1 mol L이고^–1 m은 분자성이다.^[12]

과도기 상태 이론과 아르헤니우스 이론과의 관계로부터의 추론

전환 상태 이론의 비율 상수식은 실험 속도 데이터를 사용하여 ΔG^‡, ΔH^‡, ΔS^‡ 및 ΔV^‡(활성화 볼륨)까지 계산하는 데 사용할 수 있다. 이러한 소위 활성화 매개변수는 시작 물질에 비해 에너지 함량 및 질서의 정도를 포함한 전환 상태의 특성에 대한 통찰력을 제공하며 물리적 유기 화학에서 반응 메커니즘을 해명하는 표준 도구가 되었다. 활성의 자유 에너지인 ΔG는^‡ 전환 상태 이론에서 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$= - ${\displaystyle R}$ ${\displaystyle T}$ ${\displaystyle \ln }$ ${\displaystyle {}^{}}$ ${\displaystyle {{\prime }^{}}^{}}$ ′ { { { { { { ${$ {\$displaystyle$ \$Delta$ G$^{}=-RT$\ln $K^{\dagger '}}}}}}}}}}$ hold가$$ 되도록 정의된다. 그런 다음 서로 다른 온도에서 ΔG^‡ = ΔH^‡ – ΔS를^‡ 결정하여 매개변수 ΔH와^‡ ΔS를^‡ 추정할 수 있다.

에링과 아르헤니우스 방정식의 기능적 형태가 비슷하기 때문에 활성화 파라미터와 아르헤니우스 치료의 활성화 에너지 및 프리우폰 계수를 연관시키는 것이 유혹적이다. 그러나 아르헤니우스 방정식은 실험 데이터에서 도출되었으며 메커니즘의 전환 상태 수와 관계 없이 오직 두 개의 매개변수만을 사용하여 거시적 비율을 모델링한다. 이와는 대조적으로 활성화 파라미터는 최소한 원칙적으로는 멀티 스텝 메커니즘의 모든 전환 상태에 대해 찾을 수 있다. 따라서 활성화의 엔탈피인 ΔH는^‡ 흔히 아르헤니우스의 활성화 에너지 E와_a 동일시되지만 동등하지는 않다. 응축 위상(예: 용액 위상) 또는 단분자 기체 위상 반응 단계의 경우_a E = ΔH^‡ + RT. 기타 가스 위상 반응의 경우 E_a = ΔH^‡ + (1 - Δn)^‡RT, 여기서 Δn은 전환 상태를 형성하는 분자 수의 변화다.^[13] (그러므로, 2분자 기체 위상 공정의 경우 E_a = ΔH^‡ + 2RT).

활성화의 엔트로피인 ΔS는^‡ 전환 상태(반응에 관여하거나 혼란에 빠진 용제 분자를 포함)가 시작 물질에 비해 더 혼란스러운 정도를 제공한다. It offers a concrete interpretation of the pre-exponential factor A in the Arrhenius equation; for a unimolecular, single-step process, the rough equivalence A = (k_BT/h) exp(1 + ΔS^‡/R) (or A = (k_BT/h) exp(2 + ΔS^‡/R) for bimolecular gas-phase reactions) holds. 비분자 공정의 경우, 음의 값은 지면 상태보다 더 질서 있고 단단한 전환 상태를 나타내며, 양의 값은 더 느슨한 결합 및/또는 더 큰 순응 자유를 가진 전환 상태를 반영한다. 차원성의 이유로 양분자 이상의 반응에는 선택한 표준 상태(특히 표준 농도)에 따라 달라지는 ΔS^‡ 값이 있다는 점에 유의해야 한다. 대부분의 최근 간행물의 경우 1 mol L 또는^–1 1 molar를 선택한다. 이 선택은 어금니 양과 부피에 대한 단위의 정의에 기초하여 인간의 구성이므로, 단일 반응에 대한 ΔS의^‡ 크기와 부호는 그 자체로 의미가 없다; 동일한 표준 상태에서 만들어진 "알려진" (또는 가정된) 메커니즘의 기준 반응 값과의 비교만 유효하다.^[14]

활성화 부피는 압력(유지온도 상수)과 관련하여 ΔG의^‡ 부분파생물을 취함으로써 발견된다. $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {‡}^{}}$ ${\displaystyle :=}$ (${\displaystyle \mathrm{}\Delta }$ ${\displaystyle {}^{}}$ ${\displaystyle {‡}^{}}$/ ${\displaystyle \partial \mathrm{}}$ P${\displaystyle {}_{}}$) ${\displaystyle T_{}}$ ${\$ G$^{}/\partial P$$)$${{T$ 전이 상태에서 크기, 즉 접합 정도에 관한 정보를 제공한다. 결합 메커니즘은 음의 활성화 부피를 가지는 반면, 분리 메커니즘은 양의 값을 가질 것이다.

평형 상수와 $K{\displaystyle }$ = k${\displaystyle {}_{}}$/ ${\displaystyle k{}_{}}$- ${\displaystyle 1_{}}$ ${\$Eyring 방정식은 다음을 함축한다.

${\displaystyle \mathrm{\Delta }}$ ${\displaystyle {}^{}}$ ${\displaystyle {\circ }^{}}$ =${\displaystyle {}^{}\mathrm{\Delta }}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ -${\displaystyle {}_{}^{}\mathrm{\Delta }}$ ${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$ Δ G - 1 ${\displaystyle {}_{}^{}}$ ${\$ G$^{\circ }=\Delta G_{1}^{$1}^{{1}^}\$dadager }-\\delta G_{-1$

TST의 또 다른 함축은 Curtin-Hammett 원칙이다: R에서 두 제품 A와 B에 대한 운동적으로 제어되는 반응의 제품 비율은 각각에 대한 단일 전환 상태가 있다고 가정할 때, 제품을 유도하는 각 전환 상태의 에너지 차이를 반영할 것이다.

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=e^{-\Delta \Delta G^{\ddagger }/RT}}$ (${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }}$).

(In the expression for ΔΔG^‡ above, there is an extra ${\displaystyle \Delta G^{\circ }=G_{\mathrm {S} _{\mathrm {A} }}^{\circ }-G_{\mathrm {S} _{\mathrm {B} }}^{\circ }}$ term if A and B are formed from two different species S_A and S_B in equilibrium.)

"1.36 규칙": 열역학적으로 제어되는 반응의 경우, 제품 A와 B의 자유 에너지에서 RT ln 10 ((1.987 × 10^–3 kcal/mol K)(2.303) ≈ 1.36 kcal/mol의 모든 차이는 상온(298 K)에서 선택성에 10 인수를 초래한다.

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=10^{-\Delta G^{\circ }/(1.36\ \mathrm {kcal/mol} )}}$ (${\displaystyle \Delta G^{\circ }=G_{\mathrm {A} }^{\circ }-G_{\mathrm {B} }^{\circ }}$).

이와 유사하게 활성화가 자유 에너지에서 1.36 kcal/mol 차이가 날 때마다 상온에서 키네틱으로 제어되는 공정의 선택성이 10으로 증가한다.^[15]

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=10^{-\Delta \Delta G^{\ddagger }/(1.36\ \mathrm {kcal/mol} )}}$ (${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta$$G_{\mathrm {B}^{\dadager }}}.$

야구장 수치: Eyring 방정식을 사용하면 주어진 온도에서 ΔG^‡, 1차 속도 상수, 반작용 반감기 사이에 직접적인 관계가 있다. 298 K에서 ΔG^‡ = 23 kcal/mol의 반응은 k ≈ 8.4 × 10^–5 s^–1 및 t_1/2 ≈ 2.3 시간의 반감기 비율 상수를 가지며, 종종 k ~ 10^–4 s^–1 및 t ~ 2_1/2 h로 반올림된다. 따라서 이 규모의 활성화가 가능한 에너지는 상온에서 하룻밤 사이에 완료되는 일반적인 반응에 해당한다. 비교를 위해 사이클로헥산 의자 플립은 약 11kcal/mol의 ΔG를^‡ k ~ 10s로^5–1 하여 상온에서 빠르게(NMR 타임스케일보다 빠른) 일어나는 역동적인 과정이 된다. 저울의 다른 쪽 끝에서 2-부텐의 시스/트랜스 이소머라이징은 약 60 kcal/mol의 ΔG를^‡ 가지며, 298 K에서 k ~ 10^–31 s에^–1 해당한다. 이것은 무시할 수 있는 비율이다: 반감기는 우주의 나이보다 12배나 긴 것이다.^[16]

제한 사항

일반적으로 TST는 연구자들에게 화학반응이 어떻게 일어나는지를 이해할 수 있는 개념적 기반을 제공해 왔다. 비록 그 이론이 널리 적용될 수 있지만, 그것은 한계가 있다. 예를 들어, 다단계 반응의 각 기초 단계에 적용할 때, 이론은 각 중간이 다음 단계로 계속 진행하기 전에 볼츠만 에너지 분포에 도달할 만큼 충분히 장수한다고 가정한다. 중간체들이 매우 단명할 때, TST는 실패한다. 그러한 경우 반응제로부터 중간재까지의 반응 궤적의 모멘텀은 제품 선택성에 영향을 미칠 수 있다(Anslyn과 Dougherty가 제시한 diazaobicclopentanes의 열분해).

전환 상태론도 원자핵이 고전역학에 따라 작용한다는 가정에 근거를 두고 있다.^[17] 원자나 분자가 전환 구조를 형성할 수 있을 만큼 충분한 에너지로 충돌하지 않는 한, 그 반응은 일어나지 않는다고 가정한다. 그러나 양자역학에 따르면, 에너지가 유한한 어떤 장벽에 대해서도 입자가 여전히 장벽 너머로 터널을 통과할 가능성이 있다. 화학 반응에 관하여 이것은 분자가 에너지 장벽을 통과할 수 있는 충분한 에너지와 충돌하지 않더라도 반응할 가능성이 있다는 것을 의미한다.^[18] 이 효과는 큰 활성화 에너지와의 반응에는 미미하지만, 장벽 높이가 감소함에 따라 터널링 확률이 증가하기 때문에 에너지 장벽이 상대적으로 낮은 반응에는 중요한 현상이 된다.

전환 상태 이론은 고온에서 일부 반응에 실패한다. 그 이론은 반응 시스템이 잠재적 에너지 표면의 가장 낮은 에너지 안장 지점을 통과할 것이라고 가정한다. 이 설명은 비교적 낮은 온도에서, 높은 온도에서 발생하는 반응에 대해 일관적이지만 분자는 더 높은 에너지 진동 모드를 채운다; 그들의 움직임이 더 복잡해지고 충돌은 가장 낮은 에너지 안장 지점에서 멀리 떨어진 전환 상태로 이어질 수 있다. 전환 상태 이론으로부터의 이러한 편차는 이원자 수소와 수소 급진 사이의 단순한 교환 반응에서도 관찰된다.^[19]

이러한 한계를 감안하여 전환국가 이론에 대한 몇 가지 대안이 제시되었다. 이들 이론에 대한 간략한 논의가 뒤따른다.

일반화 전이 상태 이론

전환 상태가 반드시 안장점에 위치하지 않는 미량변동변동TST, 표준변동TST, 개선된 표준변동TST와 같은 어떤 형태의 TST를 일반화된 전환상태 이론이라고 한다.

마이크로캐논 변이 TST

전환 상태 이론의 근본적인 결함은 전환 상태의 어떤 교차도 반응 물질에서 제품에 대한 반응으로 간주하거나 그 반대로 간주한다는 것이다. 실제로 분자는 이 "분열면"을 건너서 돌아설 수도 있고, 여러 번 건너갈 수도 있고, 한 번만 진정으로 반응할 수도 있다. 이와 같이 조정되지 않은 TST는 속도계수에 대한 상한을 제공한다고 한다. 이를 교정하기 위해, 변동 전이 상태 이론은 각 고정 에너지의 비율을 최소화하기 위해 성공적인 반응을 정의하는 분할 표면의 위치를 변화시킨다. ^[20] 이 마이크로캐논학적 치료에서 얻은 비율 표현은 에너지 전체에 걸쳐 통합될 수 있으며, 에너지 상태에 대한 통계 분포를 고려하여 표준 또는 열 비율을 제공할 수 있다.

표준변동TST

주어진 온도에서 일정 비율의 상수를 최소화하기 위해 분할 표면의 위치가 변화하는 전환 상태 이론의 개발.

표준변동 TST 개선

임계 에너지 이하의 에너지에 대해 분할 표면의 위치가 마이크로캐논 임계 에너지의 위치가 되는 표준 변화 전환 상태 이론의 수정. 이는 비율 상수가 임계값 에너지 미만일 경우 기여도가 0이 되도록 한다. 그런 다음 높은 에너지를 가진 반응 물질에 의한 속도 상수에 대한 기여를 최소화하기 위해 절충된 분할 표면을 선택한다.

비방사성 TST

두 개의 스핀스테이트가 동시에 관련되었을 때 TST를 반응으로 확장하는 것을 NA-TST(Nonadiabatic Transition State 이론)라고 한다.

반전설 TST

진동 섭동 이론을 사용하면 튜닝 및 변동 효과와 같은 효과를 SCTST 형식주의 내에서 설명할 수 있다.

적용들

효소반응

효소는 동일한 반응 조건에서 분석되지 않은 화학에 비해 놀라운 속도로 화학 반응을 촉진한다. 각 촉매 이벤트는 최소 3단계 또는 종종 더 많은 단계를 필요로 하며, 이 모든 단계는 전형적인 효소 반응을 특징짓는 몇 밀리초 이내에 발생한다. 전환 상태 이론에 따르면 가장 중요한 단계인 전환 상태의 단계에서 촉매 사이클의 가장 작은 부분을 사용한다. 화학 반응에 대한 절대 반응 속도 이론의 원래 제안은 절대 반응 속도를 결정하는 반응 좌표에서 전환 상태를 구별되는 종으로 정의했다. 곧이어 리너스 폴링은 효소의 강력한 촉매작용을 전환상태 종에 대한 특정한 엄격한 결합에 의해 설명할 수 있다고 제안했다.반응률은 전환상태 콤플렉스 내 반응물질의 분수에 비례하기 때문에, 효소는 반응성 종의 농도를 증가시키기 위해 제안되었다.

이 제안은 볼펜든과 노스캐롤라이나 대학교 채플힐의 동료들이 공식화했는데, 이들은 효소에 의해 부과되는 요금 인상이 마이클리스 콤플렉스에 상대적인 전이 상태 구조에 대한 효소의 친화력에 비례한다는 가설을 세웠다.^[22] 효소는 전형적으로 10-10의¹⁰¹⁵ 인자에 의한 비염산 반응률을 증가시키고, 미카엘리스^{[clarification needed]} 콤플렉스는⁻³⁻⁶ 10-10M의 범위에서 분화 상수를 갖는 경우가 많기 때문에, 전환 상태 콤플렉스는 10-10M의^{−14 −23} 범위에서 분화 상수와 결합하는 것이 제안된다. 기질이 미카엘리스 콤플렉스에서 제품으로 진행되면서 기질 내 전자분포의 효소 유발 변화에 의해 화학이 일어난다. 효소는 양성, 양성자 추상화, 전자전달, 기하학적 왜곡, 소수성 분할, 루이스 산과 염기와의 상호작용에 의해 전자 구조를 변화시킨다. 따라서 전환 상태 구조를 닮은 아날로그는 알려진 가장 강력한 비동결 억제제를 제공해야 한다.

모든 화학적 변환은 기판의 화학적 구조와 제품 사이에 있는 전환 상태라고 불리는 불안정한 구조를 통과한다. 화학 반응에 대한 전환 상태는 단일 결합 진동의 시간 순서에 따라⁻¹³ 10초 가까운 수명을 갖도록 제안된다. 효소 반응에 대한 전환 상태의 구조를 직접 관찰할 수 있는 물리적 또는 분광학적 방법은 없지만, 효소가 화학적 변환의 활성화 에너지를 낮춰 작용하기 때문에 전환 상태 구조가 효소 촉매제를 이해하는 데 중심적이다.

이제 효소가 반응제와 제품 사이에 놓여 있는 전이 상태를 안정시키기 위해 기능하며, 따라서 그것들은 그러한 전이 상태와 매우 유사한 어떤 억제제라도 강하게 결합시킬 것으로 기대된다는 것이 받아들여지고 있다. 기질과 생산물은 종종 여러 효소 촉매 반응에 참여하는 반면, 전환 상태는 한 특정 효소의 특성인 경향이 있기 때문에 그러한 억제제가 특정 효소에 특정한 경향이 있다. 수많은 전환 상태 억제제의 식별은 효소 촉매변환에 대한 전환 상태 안정화 가설을 뒷받침한다.

현재 전환 상태 아날로그와 상호작용하는 것으로 알려진 효소가 다수 존재하며, 이들 효소의 대부분은 대상 효소를 억제할 목적으로 설계되었다. 예로는 HIV-1 프로테아제, 레이스마제, β-락타마제, 메탈로프로테아제, 사이클록시제나스 등이 있다.

표면 흡착 및 표면 반응

탈착과 표면에서의 반응은 전환 상태 이론으로 설명하기 쉽다. 액체 단계에서 표면으로의 흡착 분석은 표면 근처의 용액의 농도를 평가하는 능력이 부족하기 때문에 난제를 일으킬 수 있다. 전체 세부사항을 이용할 수 없을 때, 반응하는 종의 농도를 활성 표면 현장의 농도로 정규화해야 한다고 제안되었으며, 표면 반응 물질 등밀도 근사치(SREA)라고 하는 근사치가 제안되었다.^[23]

참고 항목

• 커틴-함메트 원칙

메모들

참조

• 앤슬린, 에릭 V; 도우리, 데니스 A, 전환 상태 이론 및 관련 주제. 현대 물리 유기 화학 대학 과학 도서: 2006; 페이지 365–373
• 클랜드, W.W., 동위원소 효과: 효소 전이 상태 구조의 결정. 효소 1995, 249, 341-373의 방법
• Laidler, K.; King, C. 전이 상태 이론의 개발. 물리 화학 저널 1983, 87, (15), 2657
• 라이들러, K, 평생의 과도기-국가 이론. The Chemical Intelligence 1998, 4, 3, 39
• Radzicka, A.; Woldenden, R, Transition State 및 Multisubstit$Analog 억제제. 효소 1995, 249, 284-312의 방법
• Schramm, VL, 효소 전환 상태 및 전환 상태 아날로그 설계. 생화학 1998, 67, 693-720
• Schramm, V.L. 효소 전환 상태 이론 및 전환 상태 아날로그 설계. 생물화학 2007, 282, (39), 28297-28300

외부 링크

• TST의 간단한 적용