태양전지론

태양전지론은 광자가 적합한 반도체 소자를 타격할 때 광자의 빛에너지가 전류가 되는 과정을 설명한다.이론적 연구는 태양 전지의 근본적인 한계를 예측하고, 손실과 태양 전지 효율에 기여하는 현상에 대한 지침을 주기 때문에 실용적이다.

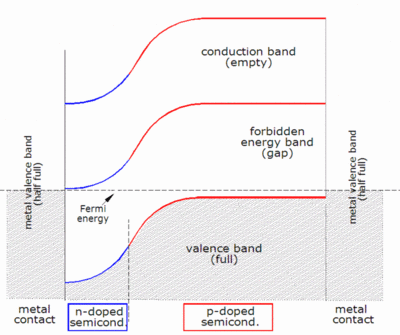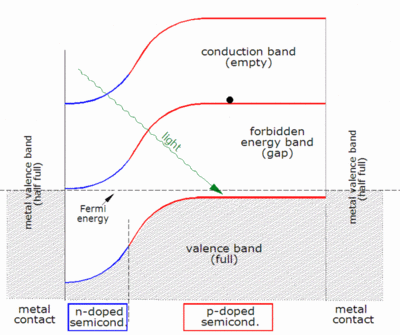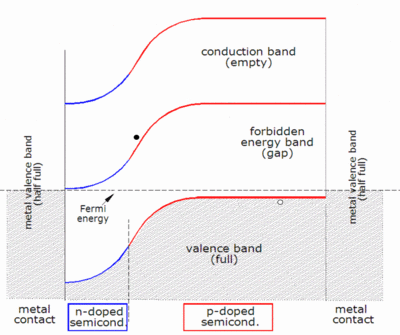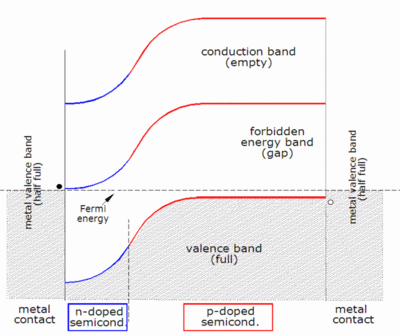
작업설명

1. 햇빛에 비친 광자는 태양 전지판에 부딪혀 반도체 물질에 흡수된다.
2. 전자(음전하)는 흥분하면서 원자로부터 느슨하게 된다.그들의 특별한 구조와 태양 전지의 물질들 때문에, 전자는 오직 한 방향으로만 움직일 수 있다.재료의 전자적 구조는 공정이 작용하는 데 매우 중요하며, 소량의 붕소나 인을 혼합한 실리콘을 다른 층에 사용하는 경우가 많다.
3. 태양 전지의 배열은 태양 에너지를 가용한 직류(DC) 전기로 변환한다.

충전 캐리어 광생성

광자가 실리콘 조각에 부딪히면, 세 가지 중 하나가 발생할 수 있다.

1. 광자는 실리콘을 곧장 통과할 수 있다. 이는 일반적으로 낮은 에너지 광자에 발생한다.
2. 광자는 표면에서 반사될 수 있다.
3. 광자에너지가 실리콘 밴드 갭 값보다 높으면 광자를 실리콘에 흡수할 수 있다.이것은 전자 홀 쌍을 발생시키고 때로는 밴드 구조에 따라 열을 발생시킨다.

광자가 흡수되면 광자의 에너지는 결정 격자 안의 전자에 주어진다.보통 이 전자는 발랑스 밴드에 있다.광자에 의해 전자에 주어지는 에너지는 그것을 반도체 내에서 자유롭게 움직일 수 있는 전도 대역으로 "흥분"한다.전자가 이전에 한 부분이었던 공밸런트 결합 네트워크는 현재 한 개의 전자를 더 적게 가지고 있다.이것은 구멍이라고 알려져 있다.공밸런트 결합이 없어지면 인접 원자의 결합 전자가 "구멍"으로 이동하여 다른 구멍을 남겨 격자 전체에 구멍을 전파할 수 있다.반도체에 흡수된 광자가 전자홀 쌍을 만든다고 할 수 있다.

광자는 발란스 대역에서 전도 대역으로 전자를 자극하기 위해 대역 간극보다 더 큰 에너지만 있으면 된다.그러나 태양주파수 스펙트럼은 약 5800K의 흑체 스펙트럼에 근사하며,^[1] 따라서 지구에 도달하는 태양 복사선의 대부분은 실리콘의 대역 간격보다 큰 에너지를 가진 광자로 구성된다.이러한 높은 에너지 광자는 태양 전지에 흡수될 것이지만, 이러한 광자와 실리콘 밴드 간격 사이의 에너지 차이는 사용 가능한 전기 에너지가 아닌 열(음파라고 불리는 격자 진동을 통해)으로 변환된다.광전 효과는 2광자 광전 효과라고 불리는 과정에서 두 광자가 동시에 흡수될 때도 발생할 수 있다.그러나 이 비선형 공정에는 높은 광학 강도가 필요하다.

p-n 접속점

가장 일반적으로 알려진 태양전지는 실리콘으로 만들어진 대면적 p-n 접합부로 구성된다.단순화로서 n형 실리콘 층을 p형 실리콘 층과 직접 접촉시키는 것을 상상할 수 있다.실제로 실리콘 태양전지의 p-n 접합은 이런 방식으로 만들어지는 것이 아니라 n형 도판트를 p형 웨이퍼의 한쪽으로 확산시켜(또는 그 반대로) 만든다.

p형 실리콘 조각을 n형 실리콘 조각과 밀접하게 접촉시키면 전자 농도가 높은 영역(접합부의 n형 측면)에서 전자 농도가 낮은 영역(접합부의 p형 측면)으로 전자가 확산된다.전자가 p-n 접합부를 가로질러 확산될 때, 그들은 p-type 측면의 구멍과 재결합한다.그러나 (외부 회로가 없는 경우) 이러한 캐리어의 확산이 무한정 진행되지 않는 것은 전하가 접속부 양쪽에 축적되어 전기장을 생성하기 때문이다.전기장은 표류 전류로 알려진 전하 흐름을 촉진하여 전자와 구멍의 확산을 방지하고 결국 균형을 맞춘다.전자와 구멍이 접속부에 걸쳐 확산된 이 지역은 사실상 이동충전 캐리어가 없기 때문에 고갈 영역이라고 불린다.우주 충전이 고갈 지역보다 양방향으로 조금 더 연장되기는 하지만 우주 충전 지역이라고도 알려져 있다.

충전 캐리어 분리

태양전지 내 전하 운반체 움직임과 분리의 원인은 두 가지가 있다.

1. 전자가 한쪽 방향으로 밀리고 다른 방향으로 구멍을 내는 전기장에 의해 움직이는 캐리어의 표류
2. 반송파 농도가 높은 구역에서 반송파 농도가 낮은 구역으로 반송파 확산(화학 전위의 기울기).

이 두 "강력"은 세포의 어느 특정 지점에서 다른 하나에 대해 작용할 수 있다.예를 들어 p영역에서 n영역으로 교차점을 이동하는 전자(이 글의 앞부분의 도표에서와 같이)는 농도 구배를 반대하여 전기장에 의해 밀리고 있다.구멍이 반대 방향으로 움직이는 것도 마찬가지다.

전기장이 강한 곳인 고갈지대에서 생성되는 전자홀 쌍을 고려할 때 전류가 어떻게 생성되는지를 가장 쉽게 이해할 수 있다.전자는 이 장에 의해 n측으로, 구멍은 p측으로 밀린다.(이것은 작동 중인 발광 다이오드와 같이 전방 바이어스 다이오드의 전류 방향과 반대다.)쌍이 전기장이 작은 공간충전구역 밖에서 생성되면 확산도 작용하여 캐리어를 이동시키지만, 접속부는 여전히 p측에서 n측으로 도달하는 어떤 전자를 쓸고, n측에서 p측으로 도달하는 어떤 구멍이라도 쓸어서 농도그라를 만드는 역할을 한다.우주 충전 구역 바깥에 있다.

두꺼운 태양전지의 경우, 우주충전 구역 바깥의 활성 지역에는 전기장이 거의 없기 때문에, 충전 캐리어 분리의 지배적 모드가 확산된다.이러한 세포에서 소수 캐리어(광생 캐리어들이 재결합하기 전에 이동할 수 있는 길이)의 확산 길이는 세포 두께에 비해 커야 한다.박막세포(아모르퍼스실리콘 등)에서는 결함의 존재로 인해 소수 캐리어들의 확산 길이가 대개 매우 짧으며, 따라서 우세한 전하 분리는 셀의 전체 두께로 확장되는 접합부의 정전기장에 의해 구동되어 표류한다.^[2]

일단 소수민족 캐리어가 표류지역에 진입하면, 접점을 가로질러 '스위프팅'되고, 접점의 반대편에서는 다수민족 캐리어가 된다.이 역류 전류는 빛의 흡수에 의해 열과 (있는 경우) 둘 다 공급되는 발전 전류다.반면에, 대다수 캐리어는 확산에 의해 표류 영역으로 유도되며(농도 구배에서 발생함), 이는 전방 전류를 유도한다; 가장 높은 에너지를 가진 대부분의 캐리어가 ( 소위 볼츠만 꼬리; cf)맥스웰-볼츠만 통계치)는 표류지역을 완전히 횡단할 수 있다.따라서 전체 장치의 반송파 분포는 역류 전류와 전방 전류 사이의 동적 평형에 의해 제어된다.

외부 부하에 대한 연결

태양전지의 n형 및 p형 면과 외부 부하에 연결된 전극에 옴금속-반도체 접점이 만들어진다.n형 측면에 생성되거나 p형 측면에 생성되는 전자는 접합부에 의해 "집합"되어 n형 측면에 쓸려가는 전자는 와이어를 통해 이동하며 부하에 전력을 공급하며 p형 반도체-금속 접촉에 도달할 때까지 와이어를 통해 계속될 수 있다.여기서 태양전지의 p형 면에 전자홀 쌍으로 만들어진 구멍이나, 거기서 만들어진 후 n형 면으로부터 분기점을 가로질러 쓸려온 구멍으로 재결합한다.

측정된 전압은 두 단자에서 다수 반송파(n형 부분의 전자자와 p형 부분의 구멍)의 준 페르미 수준 차이와 동일하다.^[3]

태양전지의 등가 회로

태양전지의 전자적 동작을 이해하기 위해서는 전기적으로 동등한 모델을 만드는 것이 유용하며, 동작이 잘 정의되어 있는 이산 이상적인 전기적 요소에 기초한다.이상적인 태양전지는 다이오드와 병렬로 전류원에 의해 모델링될 수 있다; 실제로 태양전지는 이상적이지 않기 때문에 션트 저항과 직렬 저항성분이 모델에 추가된다.^[4]태양전지의 결과 등가 회로가 오른쪽에 표시된다.또한 왼쪽에는 회로 다이어그램에 사용하기 위한 태양전지의 도식적인 표현이 표시되어 있다.

특성 방정식

등가 회로로부터 태양전지에 의해 생성되는 전류는 다이오드를 통해 흐르는 전류원을 제외하고 분로 저항기를 통해 흐르는 전류원과 동일하다는 것이 명백하다.^[5][6]

${\displaystyle I=I_{\text}L}-I_{\text{D}-I_{\text{SH}}$

어디에

• I, 출력 전류(암페어)
• I_L, 광생 전류(암페어)
• I_D, 다이오드 전류(암페어)
• 나_SH, 전류(암페어)를 션트한다.

이러한 소자를 통과하는 전류는 소자를 통과하는 전압에 의해 제어된다.

${\displaystyle V_{\text{j}=V+IR_{\text{S}}$

어디에

• V_j, 다이오드와 저항기 R의_SH 전압(볼트)
• V, 출력 단자의 전압(볼트)
• I, 출력 전류(암페어)
• R_S, 직렬 저항(Ω).

쇼클리 다이오드 방정식에 의해 다이오드를 통해 우회되는 전류는 다음과 같다.

${\displaystyle I_{\text{D}}=I_{0}\left\{\exp \left[{\frac {V_{\text{j}}{nV_{\text}}}{nV_{\text}{\text}{\text}}}}T}}}\오른쪽]-1\오른쪽\}$^[7]

어디에

• I₀, 역포화 전류(암페어)
• n, 다이오드 이상 계수(이상적 다이오드의 경우 1)
• q, 기본 충전
• k, 볼츠만의 상수
• T, 절대 온도
• ${\displaystyle V_{\text{$T$}}=kT/q,}$ 열전압.25°C에서 $V{\displaystyle {}_{}}$ ${\displaystyle T_{}}$ ${\displaystyle \mathrm{\approx }}$ 0.${\displaystyle 0259}$ ${\displaystyle V_{\text{$$T}}\$ 약$0.0259}$볼트$$.

옴의 법칙에 따르면 션트 저항기를 통해 우회되는 전류는 다음과 같다.

${\displaystyle I_{\text{SH}}={\frac {V_{\text{j}{R_{\text}}{R_{\text{\text}}{\text}{\textsh}}}$

어디에

• R_SH, 션트 저항(Ω).

이를 첫 번째 방정식으로 대체하면 태양전지의 특성 방정식이 생성되며, 이는 태양전지 매개변수를 출력 전류와 전압과 연관시킨다.

${\displaystyle I=I_{\text}L}-I_{0}\왼쪽\{\exp \left[{\frac {V+IR_{\text{S}}{nV_{\text{T}}}}\오른쪽]-1\오른쪽\}-{\frac {V+IR_{\text{S}}{R_{\text{SH}}}.}$

대체 파생은 외관상으로는 유사한 방정식을 만들지만, 왼쪽에는 V가 있다.두 가지 대안은 정체성이다. 즉, 그들은 정확히 같은 결과를 산출한다.

변수 I₀, n, R_S, R을_SH 직접 측정할 수 없기 때문에 특성 방정식의 가장 일반적인 적용은 이들 매개변수가 태양전지 거동에 미치는 결합된 영향을 기초로 이들 매개변수의 값을 추출하는 비선형 회귀 분석이다.

R이_S 0이 아닐 때, 위의 방정식은 전류 I를 직접 부여하지 않지만, Lambert W 함수를 사용하여 해결할 수 있다.

${\displaystyle I={\frac {(I_{\text}{L}}+I_{0}-V/R_{\text{SH}}{1+R_{\text{S}/R_{\text}{\text{SH}}-{\frac {nV_{\text{T}}{R_{\text{S}}}W\left({\frac {I_{0}R_{\text}{S}}{nV_{\text{T}}(1+R_{\text{S}/R_{\text}{SH}}}}\exp \left({\frac {V}{nV_{\text{T}}}}\왼쪽(1-{\frac {R_{\text{S}}{R_{\text{S}+R_{\text{SH}}}\오른쪽)+{\frac {(I_{\text}{L}}+I_{0}R_{\text{S}}{nV_{\text{T}}(1+R_{\text{S}/R_{\text}{Sh}}}}\오른쪽)\오른쪽)}$

외부 부하를 셀과 함께 사용할 경우, 전류를 찾기 위해 R과_S V가 0으로 설정된 것에 간단히 저항을 추가할 수 있다.

R이_SH 무한대일 ${\displaystyle {때}_{}}$I ${\displaystyle {}_{}}$ + I ${\displaystyle 0_{}}$보다 작은$$I {\$displaystyle$ I$}$에 대해 V에 대한 솔루션이 있음${\text}$$L}}+I_{0}$:

${\displaystyle V=nV_{\text{T}\ln \left({\frac {I_{\text}{L}-I}{I_{0}}+1\오른쪽)-IR_{\text{S}}.}$

그렇지 않으면 Lambert W 기능을 사용하여 V에 대해 해결할 수 있다.

${\displaystyle V=(I_{\text}L}}+I_{0}R_{\text{SH}-I(R_{\text{S}+R_{\text{SH}}-nV_{\text{T}}W\left({\frac {I_{0}R_{\text}{SH}}{nV_{\text{T}}}\exp \left({\frac {(I_{\text}){L}}+I_{0}-I)R_{\text{SH}}{nV_{\text{T}}}\오른쪽)\오른쪽)$

그러나 R이_SH 클 때는 원래 방정식을 숫자로 푸는 것이 좋다.

용액의 일반적인 형태는 V가 증가할수록 I이 감소하는 곡선이다(아래 그래프 참조).작은 V 또는 음의 V에서의 기울기(W 함수가 0에 가까운 경우)는 $-{\displaystyle 1}$/ ( ${\displaystyle R_{}}$S + ${\displaystyle {}_{}}$ ${\displaystyle {\text{SH}}_{}}$)에 접근한다. - ${\displaystyle -1/(R_{\text${\text$}$$S}+R_{\text{$$SH$ 높은 V에서의 기울기가 -${\displaystyle 1}$/ R ${\displaystyle S_{}}$ ${\$$S$

개방 회로 전압 및 단락 전류

셀이 개방회로에서 동작할 때 I = 0이며 출력단자 전체의 전압은 개방회로 전압으로 정의된다.션트 저항이 특성 방정식의 최종 항을 무시할 정도로 높다고 가정하면, 개방 회로 전압 V는_OC 다음과 같다.

${\displaystyle V_{\text{OC}}\약 {\frac {nkT}{q}\ln \left({\frac {I_{\text})L}}{I_{0}}+1\오른쪽).}$

마찬가지로 셀이 단락 회로로 동작할 때 V = 0이며 단자를 통과하는 전류 I는 단락 전류로 정의된다.고품질 태양전지(낮은 R과_S I₀, 그리고 높은_SH R)의 경우 내가_SC 다음과 같은 단락 전류임을 알 수 있다.

${\displaystyle I_{\text{SC}}\ 관련 I_{\text{L}}.}$

단선 또는 단락 조건에서 작동할 때는 장치에서 전력을 추출할 수 없다.

물리적 크기의 영향

I_L, I₀, R_S, R의_SH 값은 태양 전지의 물리적 크기에 따라 달라진다.그렇지 않으면 동일한 셀을 비교할 때, 원칙적으로 다른 의지의 접속 면적이 두 배인 셀은 광암호화폐가 생성되고 다이오드 전류가 흐를 수 있는 면적이 두 배 있기 때문에 I와_L I를₀ 두 배로 한다.동일한 논거에 의해 수직 전류 흐름과 관련된 직렬 저항의 절반_S R도 갖게 되지만, 대면적 실리콘 태양 전지의 경우, 가로 전류 흐름에 의해 마주치는 직렬 저항의 스케일링은 그리드 설계에 결정적으로 좌우되기 때문에 쉽게 예측할 수 없다(그렇지 않으면 어떤 "동일한" m이 될지는 명확하지 않다).이 점에서는 eans).션트 유형에 따라, 큰 셀은 션트가 발생할 수 있는 면적의 두 배가 있기 때문에 R의_SH 절반을 가질 수도 있다. 반면에, 션트가 주로 둘레에서 발생한다면, R은_SH 면적이 아닌 둘레의 변화에 따라 감소할 것이다.

전류의 변화가 지배적인 것이며 서로 균형을 맞추고 있기 때문에, 개방 회로 전압은 사실상 같다; V는_OC R이_SH 너무 낮아질 경우에만 셀 크기에 의존하기 시작한다.전류의 우세를 설명하기 위해 특성 방정식은 전류 밀도 또는 단위 셀 영역당 생성되는 전류로 자주 작성된다.

${\displaystyle J=J_{\text}L}-J_{0}\왼쪽\{\exp \left[{\frac {q(V+Jr_{\text{S})}{nkT}}\오른쪽]-1\오른쪽\}-{\frac {V+Jr_{\text{S}}{r_{\text{sh}}}$

어디에

• J, 전류 밀도(암페어/cm²)
• J_L, 광생 전류 밀도(암페어/cm²)
• J₀, 역포화 전류 밀도(암페어/cm²)
• r_S, 특정 직렬 저항(Ω·cm²)
• r_SH, 특정 션트 저항(Ω·cm²).

이 공식은 몇 가지 장점이 있다.하나는 셀 특성이 공통 단면적을 참조하기 때문에 다른 물리적 치수의 셀과 비교될 수 있다는 점이다.이는 모든 셀의 크기가 같은 경향이 있는 제조 환경에서 제한된 효용이지만, 연구와 제조사 간의 셀 비교에 유용하다.또 다른 장점은 밀도방정식이 매개변수 값을 자연스레 비슷한 규모의 순서로 스케일링해 순진한 해법으로도 수치 추출을 단순하고 정확하게 할 수 있다는 점이다.

이 공식에는 실질적인 한계가 있다.예를 들어, 특정 기생 효과는 세포 크기가 줄어들면서 중요성이 커지며 추출된 파라미터 값에 영향을 미칠 수 있다.접합부의 재조합과 오염은 셀의 둘레에서 가장 큰 경향이 있으므로 매우 작은 셀은 그렇지 않으면 동일한 큰 셀보다 더 높은 값₀ J 또는 낮은 값 R을_SH 나타낼 수 있다.이러한 경우, 세포간의 비교는 주의 깊게 그리고 이러한 효과를 염두에 두고 이루어져야 한다.

이 접근방식은 태양 전지를 유사한 레이아웃과 비교하는 데만 사용해야 한다.예를 들어, 전형적인 결정 실리콘 태양전지와 같은 주로 4차원 태양전지와 일반 박막 태양전지와 같이 좁지만 긴 태양전지를 비교하는 것은 다른 종류의 전류경로에 의해 야기되는 잘못된 가정으로 이어질 수 있으며, 따라서 분산된 직렬 저항기여의 영향도 있을 수 있다.대 r_S.^[8][9] 태양 전지의 매크로 아키텍처는 특히 박막 태양 전지와 고도로 복잡하게 접힌 구조를 허용할 수 있는 유연한 태양 전지의 경우 고정된 부피에 다른 표면 영역을 배치할 수 있다.부피가 결합 제약 조건인 경우, 표면적에 기초한 효율성 밀도는 덜 관련성이 있을 수 있다.

투명 전도성 전극

투명한 전도성 전극은 태양 전지의 필수적인 구성 요소다.인듐 주석 산화물의 연속 필름이나 전도 배선 네트워크 중 하나로, 전선 사이의 공극은 빛을 위해 투명하지만 전선은 충전 수집기 역할을 한다.배선 밀도가 높을수록 광 투과율이 차단되는 반면, 배선 밀도가 낮을수록 충전 캐리어 이동 거리가 많아져 재결합 손실이 커지기 때문에 최적의 배선 네트워크 밀도는 최대 태양전지 성능을 위해 필수적이다.^[10]

세포온도

온도는 두 가지 방식으로 특성 방정식에 영향을 미친다. 즉, 지수 기간의 T를 통해, 그리고 I에₀ 대한 영향을 간접적으로 받는다(엄밀히 말하면 온도는 모든 항에 영향을 미치지만, 이 두 항은 다른 항보다 훨씬 더 유의하다).T를 증가시키면 특성 방정식에서 지수의 크기가 감소하지만, I의₀ 값은 T와 함께 기하급수적으로 증가한다.순효과는 온도가_OC 증가함에 따라 V(개방 회로 전압)를 선형적으로 감소시키는 것이다.이 감소의 크기는 V에_OC 반비례한다. 즉, V 값이_OC 더 높은 셀은 온도가 증가함에 따라 전압 감소가 더 적다.대부분의 결정 실리콘 태양 전지의 경우 V의_OC 온도가 -0.50%/°C이지만, 최고 효율의 결정 실리콘 전지의 속도는 -0.35%/°C이다.비교해 보면, 아모르퍼스 실리콘 태양전지의 비율은 셀이 어떻게 만들어지느냐에 따라 -0.20~ -0.30%/°C이다.

광생성 전류 I의_L 양은 온도가 증가함에 따라 약간 증가하는데, 이는 셀에서 열 발생 캐리어의 수가 증가하기 때문이다.그러나 이 효과는 미미하다. 결정 실리콘 셀의 경우 약 0.065%/°C, 비정형 실리콘 셀의 경우 0.09%이다.

세포 효율성에 대한 온도의 전반적인 영향은 특성 방정식과 조합하여 이러한 요인을 사용하여 계산할 수 있다.그러나 전압의 변화가 전류 변화보다 훨씬 강하기 때문에 효율성에 대한 전체적인 영향은 전압에 대한 것과 유사한 경향이 있다.대부분의 결정 실리콘 태양전지는 0.50%/°C의 효율이 떨어지고, 대부분의 비정형전지는 0.15-0.25%/°C의 효율이 떨어진다.위의 그림은 다양한 온도에서 결정 실리콘 태양 전지에 대해 일반적으로 볼 수 있는 I-V 곡선을 보여준다.

직렬 저항

직렬 저항이 증가하면 접속 전압과 단자 전압 사이의 전압 강하가 동일한 전류에 대해 커진다.그 결과 I-V 곡선의 전류 제어 부분이 원점을 향해 처지기 시작하여 단자 전압 V가 크게 감소하고 단락 전류인 I가_SC 약간 감소한다.R의_S 매우 높은 값은 또한_SC I에 상당한 감소를 가져올 것이다; 이러한 체제에서는 직렬 저항이 지배적이고 태양 전지의 동작이 저항의 그것과 유사하다.이러한 효과는 오른쪽 그림에 표시된 I-V 곡선의 결정 실리콘 태양 전지에 대해 나타난다.

직렬 저항으로 인한 손실은 P_loss = VI_Rs = IR로²_S 주어진 첫 번째 근사치에서 발생하며 (사진-) 전류로 2차적으로 증가한다.따라서 높은 조명 강도에서는 직렬 저항 손실이 가장 중요하다.

션트 저항

분로 저항이 감소함에 따라 분로 저항을 통해 우회되는 전류는 주어진 연결 전압 레벨에서 증가한다.그 결과 I-V 곡선의 전압 제어 부분이 원점으로부터 멀리 처지기 시작하여 단자 전류 I가 크게 감소하고 V가_OC 약간 감소한다.R_SH 값이 매우 낮으면 V가_OC 상당히 감소할 것이다.높은 직렬 저항의 경우와 마찬가지로 심하게 위축된 태양 전지는 저항기와 유사한 작동 특성을 가질 것이다.이러한 효과는 오른쪽 그림에 표시된 I-V 곡선의 결정 실리콘 태양 전지에 대해 나타난다.

역포화 전류

무한 션트 저항을 가정할 경우 V_OC:

${\displaystyle V_{\text{OC}}={\frac {kT}{q}\ln \left({\frac {I_{\text}{\frac{\text})SC}}{I_{0}}+1\오른쪽).}$

따라서 I의₀ 증가는 증가 로그의 역에 비례하는 V의_OC 감소를 산출한다.이는 위에서 설명한 온도 상승에 수반되는 V의_OC 감소 이유를 수학적으로 설명한다.결정 실리콘 태양전지의 I-V 곡선에 대한 역포화 전류의 영향은 오른쪽 그림에 나타나 있다.물리적으로 역포화 전류는 역방향 바이어스 방식으로 p-n 접합부를 가로지르는 캐리어의 "유출"을 측정한 것이다.이 누출은 연결부 양쪽의 중립 영역에서 반송파가 재결합한 결과다.

이데올로기성 인자

이데올로기성 인자(유효성 인자라고도 함)는 다이오드의 동작이 이론에 의해 예측된 동작과 얼마나 밀접하게 일치하는지 설명하는 피팅 파라미터로, 다이오드의 p-n 접합부는 무한 평면이며 공간충전 영역 내에서 재결합이 발생하지 않는다고 가정한다.n = 1일 때 이론과 완벽하게 일치하는 것으로 표시된다.그러나 공간충전 영역에서 재조합이 다른 재조합을 지배하는 경우 n = 2.다른 모든 파라미터와 독립적으로 이상성 계수를 변화시키는 효과는 오른쪽 그림에 표시된 I-V 곡선의 결정 실리콘 태양전지에 대해 나타난다.

기존 다이오드에 비해 상당히 큰 대부분의 태양 전지는 무한 평면과 거의 비슷하며, 일반적으로 표준 시험 조건(n ≈ 1)에 따라 거의 이상행동을 보일 것이다.그러나 특정 작동 조건에서 기기 작동은 공간 충전 구역의 재결합에 의해 지배될 수 있다.이는 Ⅰ이₀ 크게 증가함은 물론 관념성 인자가 n Ⅱ 2로 증가한 것이 특징이다.후자는 태양전지 출력 전압을 증가시키는 반면 전자는 이를 잠식하는 작용을 한다.따라서 순효과는 오른쪽 그림에서 n을 증가시키기 위해 표시된 전압의 증가와 위의 그림에서 I를₀ 증가시키기 위해 표시된 전압의 감소의 조합이다.전형적으로, 나는₀ 더 중요한 요인이고 그 결과는 전압의 감소다.

때때로 이상인자가 2보다 큰 것으로 관찰되는데, 이는 일반적으로 태양전지에 쇼트키 다이오드나 이질결합이 존재하기 때문이라고 한다.^[11]이형 접합 오프셋의 존재는 태양 전지의 수집 효율을 감소시키고 낮은 충만 인자의 원인이 될 수 있다.

참고 항목

• 기전력 § 태양전지

참조

외부 링크

• PV 등대 등가 회로 계산기
• 화학 설명 - chemistryexplained.com의 태양 전지