스트렐 건설

스트렐의 구조는 특정한 이성적인 강화 음악적 튜닝에서 음의 투구에 대한 균일한 직경과 장력을 가진 일련의 진동 스트링의 길이를 결정하는 기하학적 방법이다.1743년 스웨덴 왕립과학원 회보에 스웨덴의 마스터 오르간 제작자 다니엘 스트롤(1700–1746)이 처음 발표하였다.아카데미 서기관 제이콥 파고트가 잘못 계산된 투구 세트를 기사에 추가했고, 이 수치들은 1776년 베르수흐 뷔르 다이에 뮈시칼리스체 템퍼레이터에서 프리드리히 빌헬름 마르푸르에 의해 재현되었다.1800년경에 출판된 몇몇 독일 교과서들은 그 실수가 1779년 Christlieb Benedikt Funk에 의해 처음 확인되었다고 보고했지만, 튜닝 이론가 J. Murray Barbour가 그것을 거의 동등한 기질과 s를 비교하는 좋은 방법으로 제시했던 20세기 중반까지 그 건설 자체는 거의 주목을 받지 못한 것으로 보인다.작은 뿌리의 유사 지수 그리고 그것의 기초적인 수학적 원리를 일반화했다.

수학자 이언 스튜어트와 아이작 제이콥 쇤베르크의 기사를 통해 초조해 하는 악기를 만드는 장치로 알려지게 되었으며, 이들로부터 교육을 받지 않은 장인이 개발한 독특하고 현저히 우아한 해법으로 칭송받고 있다.

최근 영어 작품에 사용된 '스트라흘(Strahle)'이라는 명칭은 마르푸르트의 텍스트에 표기 오류로 나타나는데, 이때 'e'가 올라간 고리를 대신한 구식 이아크리트어(^[1]diacritic이 사용된 것으로 보인다.

배경

다니엘 P.스트롤은 18세기 2/4분기에 스웨덴 중부에서 오르간 제작자로 활동했다.그는 스톡홀름의 중요한 오르간 건축가 요한 니클라스 카만의 여정공으로 일했으며, 카만이 죽은 지 4년 뒤인 1741년 스트롤은 오르간 제작에 대한 특권을 부여받았다.당시 스웨덴에서 시행된 제도에 따르면, 각 악기 종류별로 가장 확립된 소수의 메이커만이 보유하고 있던 허가된 독점권은 그에게 장기를 만들고 수리할 수 있는 법적 권리는 물론 노동자의 훈련과 검진권을 주었으며, 업무와 교육의 질을 보장하는 역할도 했다.제조자의 ^[2]이온1743년부터 그가 만든 장기는 스트룀스홀름 궁전의 예배당에 원래 상태로 보존되어 있으며,^[3] 클라비코드를 만든 것으로도 알려져 있으며, 그가 서명한 특이한 현악 스케일과 1738년의 날짜를 가진 주목할 만한 예가 스톡홀름 음악 박물관이 소장하고 있다.^[4]그의 도제들 그의 책 Historisk Afhandling om Musik Instrumenter och 1773년에 출판된 Stråhle에서 직접 이렇게 mathemati가 포함된 것으로 추정되었었다 역학을 공부하고 있었습니다 그의 조카 페테르 Stråhle 그리고 조나스 수류탄, 그 유명한 스톡홀름 기관 건설 업체 수류탄 및에서 파트너, Stråhle,[5]와 아브라함 Abrahamsson Hülphers에 따라 포함했다.cs[6])wi스웨덴 과학 아카데미의 설립 멤버 크리스토퍼 폴헴.^[7]그는 1746년 북부 우플랜드의 뢰브스타브룩에서 사망했다.

스트롤은 새로 결성된 스웨덴 왕립과학원(Royal Swedswedish Academy of Sciences)의 과정 4권에 등장한 글에서 "조정에 있어서의 기질을 결정하기 위한 새로운 발명품, 클라비코드와 이와 유사한 악기의 투구를 위한 기질을 결정하기 위한 것"이라고 자신의 건축물을 발표했는데, 여기에는 저명한 학자들과 아카데미 회원 폴헴의 기사가 포함되어 있었다., 칼 린네우스, 칼 프레드릭 메넌더, 아우구스틴 에렌스베르트, 사무엘 클링겐스티에나.아카데미에서 강도 높은 논쟁의 1740s,[8]동안 장기 학자. 에바는 헬레니 어스 음악 튜닝에 따르면 주제, 그리고 Stråhle 자기 자신을 멤버가 아님 그의 실용적인 뮤지컬 주제에 세번째 기사는 Academy—the 처음으로 두 갈래에 의해 출판되었다 아마추어 뮤지컬 악기 제작자, 주례자 아카데미 회원 닐스 Brelin[9]가 있었다.rela하프시코드와 클라비코드에 적용할 수 있는 ^[10]테드 발명품

스트롤은 자신의 글에서 자신이 귀의 성질을 가장 부드럽게 만드는 기질("스페프닝가")의 끈의 길이에 대한 계량기를 만들 목적으로 "일부 사색과 수많은 시도"로 그 방법을 개발했으며, 또한 가장 유용하고 고른 배열로 구성되어 있다고 썼다.그는 공을 던진다.그의 지침은 같은 기간 동안 발표된 더 잘 알려진 튜닝과 유사한 강화 간격을 가진 불규칙한 튜닝을 생산하지만, 그는 튜닝 자체에 대한 더 이상의 논평이나 설명을 제공하지 않았다. 오늘날에는 일반적으로 동일한 기질의 근사치로 간주된다.^[11]그는 또한 직선자와 칸막이로만 계산이나 측량 없이 정확하고 반복 가능한 결과를 산출할 수 있는 자신의 공사의 어떤 장점도 자세히 설명하지 않았다; 그는 이 공사에 대해 단 다섯 단계로만 기술했으며, 돔 베도스 드 셀레스(Dom Bédos de Celles)가 o를 결정하는 산술법에 의해 기술된 산술적 방법보다 덜 반복적이다.Rgan pipe length intonation 또는 Vincenzo Galilei가 근사적으로 동일한 기질에서 끈을 조이는 위치를 결정하기 위한 Vincenzo Galilei, 그리고 Gioseffo Zarlino와 Marin Merssenne이 기술한 기하학적 방법들, 이 모든 것들이 Stråle의 것보다 훨씬 더 잘 알려져 있다.스트롤은 이 시스템을 클라비코드에 적용했다고 진술하면서 결론을 내렸다. 비록 튜닝뿐만 아니라 음향 길이 결정 방법도 많은 다른 악기에도 사용할 수 있지만, 기사에 기술된 두 가지 예시 외에 그것이 더 널리 행해졌는지를 보여주는 증거는 거의 없다.오늘 행방이 묘연해

건설

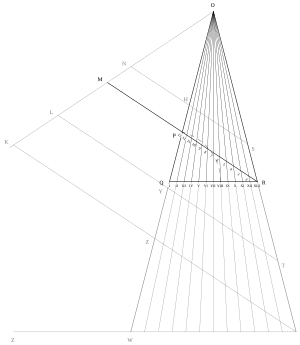
스트롤은 먼저 편리한 길이의 QR을 12개의 동일한 부분으로 나누도록 지시했고, 포인트는 I부터 XII까지라고 표시했다.QR은 측면 OQ와 OR이 QR보다 두 배 긴 삼각형 이소세슬의 베이스로 사용되며, 꼭지점 O에서 밑면의 각 번호 지점을 통과하는 광선을 그린다.마지막으로, 선은 R에서 P로 두 배 거리에 위치한 Q에서 M 지점까지 7단위로 삼각형의 반대쪽 다리의 P 지점을 통과하는 각도에서 정점 R에서 그려진다.MR의 길이는 가장 낮은 소리 내는 피치의 길이와 MP의 길이를 구성에 의해 생성된 문자열 길이 중 가장 높으며, 이들 사이의 소리 내는 길이는 라벨이 1에서 12까지인 선 O I ~ O XII가 있는 MR의 교차점까지의 거리에 의해 결정된다.

Stråhle wrote that he had named the line PR "Linea Musica", which Helenius noted was a term Polhem had used in an undated but earlier manuscript now located at the Linköping Stifts- och Landsbibliotek and which is accompanied by notes from composer and geometer Harald Vallerius (1646–1716) and Stråhle's former employer J. N. Cahman.^[8]

스트롤은 또한 한번 만들어진 건설이 어떻게 다른 선발 투구를 수용하도록 확장될 수 있는지를 설명하기 위해 NHS, LYT, KZV를 통해 MR에 평행한 라인 세그먼트를 보여주었다.

스트롤은 글의 결론에서 이 구간이 자신이 쓴 모노코드처럼 동일한 긴장 상태에서 동일한 게이지 와이어로 모두 걸렸을지는 불분명하지만, 그가 누구의 구문을 더 상세히 기술했는지는 불분명하지만, 클라비코드의 가장 높은 3 옥타브에 현악 스케일을 구현했다고 진술했다.그러나 그는 단지 그것의 튜닝을 설정하는 간접적인 방법을 설명했을 뿐인데, 그는 먼저 열린 문자열이 이전에 일제히 튜닝된 13개의 문자열 모노코드의 이동 가능한 다리에 해당하는 문자열 길이를 전달함으로써 기준 피치를 설정하도록 요구하였다.^a

패고트 수식 표현

스트롤의 뒤를 이은 기사는 당시 과학아카데미 서기관이자 미래 측량실 책임자인 제이콥 패고(1699~1777)가 이를 수학적 취급한 것으로, 같은 권의 양철 무게 측정과 통의 부피 계산 방법에 관한 기사도 기고했다.패고는 아카데미 초대 회원 중 한 명이었으며, 도량형 및 대책 특별 위원회의 회원이기도 했다.^[12]헬렌리우스는 자신이 수학적 관점에서 음악 주제에 관심이 있다고 묘사하고 아카데미를 통해 주기적으로 악기 제작자들과 접촉했다고 기록했지만 그는 음악가는 아닌 것 같다.^[13]헬레니우스는 또한 그녀가 제안한 1756년 요한 브로만이 만든 두 개의 실험용 악기에 사용된 긴 테너 현을 스웨덴에 건설된 클래비코드의 유형에 영향을 미쳤다고 주장하면서, 파고트가 스웨덴의 악기 제작에 간접적이고 사후적인 영향을 주었다면 더욱 적극적인 이론을 제시했다.18세기 후반과 ^[14]19세기 초에

Faggots와 Stråle의 끈 길이와 상대 투구

주석을 달다	포고트		스트롤[15]
주석을 달다	길이	센트	길이	센트	비율
C	10000	0	10000	0	1/1
c ♯	9379	111	9432	101	211/199
d	8811	219	8899	202	109/97
d ♯	8290	325	8400	302	25/21
e	7809	428	7930	401	29/23
f	7365	529	7490	500	239/179
f ♯	6953	629	7073	600	41/29
g	6570	727	6676	699	253/169
g ♯	6213	824	6308	798	65/41
a	5881	919	5955	897	89/53
♯.	5568	1014	5621	997	137/77
b	5274	1108	5303	1098	281/149
c	5000	1200	5000	1200	2/1

스트롤의 기사 Faggot은 스트롤의 글에서 스트롤의 방법에 의해 생산된 새로운 튜닝과 순수한 3분의 1, 4분의 5의 튜닝(표에는 "N.1"로 표기됨) 및 동등한 기질과의 튜닝을 비교하기 위해 그가 개별 투구의 소리 내는 길이를 계산하기 위해 사용했던 삼각계 단계를 간략히 설명했다.ly "더 나이든 기질과 매튜슨 씨의 비평가 음악" ("N.2") 그는 "이전에 설명한 발명에 따른 음조의 튜닝이 듣기 좋은 소리와 더 나은 고른 음성으로 귀를 만족시키는지, 그리고 키보드 악기의 악보에서 그 결과의 수치를 나타내려고 했다.선행학습은 귀가 듣는 것을 눈으로 볼 수 있을 때, 오래되고 이전에 알려진 튜닝 방식보다 더 잘 판단할 수 있다."

두개의 기사 아카데미의 소송 절차를 독일판 1751,[16]에 게재된과 Faggot 계산된 문자열 길이의 테이블에 Marpurg에 의해 그의 1776년 Versuch에 포함되어 있어 재생되었습니다 über 다이 musikalische Temperatur,[1]는 저술한 그는 오겠다고 그들의 정확성지만 후보보다 조화를 이뤄"Strähle"의 정해진 목표, th.etuning는 불평등한 기질을 "용서할 수 있는 타입도 아니다"^[1]라고 표현했다.

그sounding 길이 Faggot으로 계산한 실질적으로 무엇 Stråhle의 지시에 따라 생산될 것에서 처음 Christlieb 베네딕트 펑크에 의해 Dissertatio 드 소노 44.1도노에서 1779,[17]에 발표되었고, 그가 만든 튜닝 간격은 범위를 벗어나는 동조를 포함한 사실 전통적으로 i. 사용하던 다른 있n우리는근엄한 예술 음악펑크는 1791년 게를러의 피시칼리스치 뷔르터부치,^[18] 1804년 피셔의 피시칼리스치 뷔르터부치에서 이러한 불일치를 관찰한 공로를 인정받고 있으며,^[19] 1830년 다이 아쿠스티크의 에른스트 클라드니가 이 오류를 지적하였다.^[20]같은 기간 스웨덴에서도 비슷한 논평이 나온 적이 없는 것으로 보인다.

이 작품들은 로그 테이블의 사인 컬럼 대신 접선의 값을 사용한 결과로 Faggot의 실수를 보고한다.오차 자체는 RP의 각도를 7도 정도로 너무 크게 만드는 것으로 구성돼 QP의 유효 길이가 8.605로 늘어났다.이것은 그가 기사에서 스트롤의 구성이나 기질에 대해 더 이상 언급하지 않았기 때문에 파고가 이러한 명백한 결함을 관찰했는지는 분명하지 않지만, 그가 그 옆에 제시했던 튜닝에 비해 기질의 오류를 크게 과장했다.

튜닝

스트롤의 지시에 따라 만들어진 튜닝은 5분의 1에서 704센트의 범위를 가진 이성적 기질인데, 이것은 평균적인 5분의 1에서 2센트인 3분의 1에서 2센트인 3분의 1정도의 가격보다 약 1 센트 높은 가격이다; 3분의 1은 396 센트에서 404 센트, 또는 5/4에서 3센트의 가격인 10 센트밖에 되지 않는다.이러한 간격은 수용 가능한 것으로 간주되는 범위 내에 속하지만 17세기와 18세기에 발표된 곡들 중 오늘날 가장 인기 있는 것을 특징짓는 더 자주 사용되는 키에 대한 더 나은 3분의 1의 분포는 없다.가장 좋은 5번째는 F♯의 키 즉, MB가 주는 피치에서 순수하며, 가장 좋은 3번째는 697%의 5분의 1인 키 E이다. 두 구간의 가장 좋은 조합은 F의 키에 있고 최악의 조합은 B b의 키에 있다.

바르보어의 대수적 표현과 기하학적 구조

J. Murray Barbour는 20세기 Faggot의 그것에 대한 치료와 함께 Stråle의 건설에 새로운 관심을 가져왔다.마르푸르의 맥락에서 소개된 그는 1951년 저서 튜닝과 기질에서 끈 길이를 결정하는 더 유명한 방법과 함께 그것의 개요를 포함시켰는데, 이 책에서 그는 이 튜닝을 "평등한 기질에 대한 근사치"라고 묘사했다.그는 또한 Strlele의 구조가 그 방법이 제공할 수 있는 최선의 근사치에 얼마나 가까운지를 보여주었는데, 이것은 3분의 1과 5분의 1의 주요 오차를 약 절반으로 줄이고 7.028을 QP의 길이로 대체함으로써 달성된다.

Barbour는 6년 후 American Mathemical Monthly지에 게재된 "숫자의 뿌리에 대한 기하학적 근사"에서 이 구조에 대한 보다 완벽한 분석을 제시했다.^[21]그는 페이고의 오류와 그 결과를 검토한 다음 유사한 삼각형을 사용하여 스트롤의 건설을 대수적으로 도출했다.이것은 일반화된 형태를 취한다.

${\displaystyle N^{m}\doteq {\frac {OA+BA+(OA-3BA)\time{m}}{{m}}{OA+BA-2BA\time{m}}}}}$

Stråle의 지시사항의 값을 사용하여

${\displaystyle {\frac {24+10m}{24-7m}}$

${\displaystyle \mathrm{O}}$ ${\displaystyle A}$- B ${\displaystyle A}$= 1 ${\$}을$($를) 허용하여 ${\displaystyle OA\sqrt{}}$+ ${\displaystyle B}$ A${\displaystyle }$= N ${\$\script $style OA+$$BA={\sqrt{N}}$는 계산에 더 유용한 첫 번째 공식의 형태로 이어진다.

${\displaystyle N^{m}\doteq {\frac {Nm+{\sqrt{{N}(1-m)}{m+{\sqrt{N}}}}}}$

그런 다음 Barbour는 원본에서 요구하는 대부분의 특정 각도와 길이를 회피하는 MB 길이에 대해 쉽게 얻은 평균 비율을 사용하여 일반화된 구조를 설명했다.음악적 어플리케이션의 경우 스트롤보다 간단하고 결과가 약간 더 균일하며, 추가 스케일링 없이 원하는 스트링 길이를 연출할 수 있는 장점이 있다.

그는 우선 MP로 두 숫자 중 더 큰 숫자에 해당하는 MR 선을 더 작게 그리고 평균 비례 MB로 구성하라고 지시했다.분할을 운반할 선은 어느 급각에서든 R에서 MR로 그리고, 그 선에 수직인 선은 B를 통해 그려지며, A에서 분할할 선과 교차하며, RA가 Q로 확장되어 RA=가 된다.AQ. O에서 BA를 통과하는 선과 교차하는 Q에서 P까지 선을 그리고 O에서 R까지 선을 그린다.QR과 드로잉 광선을 O에서 각 사단을 거쳐 나눠 공사가 완료된다.

Barbour는 다른 뿌리의 지수 근사치를 위해 사용될 때 일반화 공사에 의해 발생하는 오류의 패턴과 크기에 대한 토론으로 결론을 내렸으며, 그의 방법은 "단순하고 소수에 비해 매우 잘 작동한다"고 말했다.1에서 2까지의 루트의 경우 오차는 0.13%(N=2일 때 약 2센트)보다 작으며 m=0.21과 m=0.79의 경우 최대값이 된다.오차 곡선은 대략 정현상으로 나타나며, $이{\displaystyle }$ N 범위의 경우 N=1, ${\displaystyle f}$( m${\displaystyle }$)${\displaystyle }$= ${\displaystyle \mathrm{m}}$( ${\displaystyle 1}$- m${\displaystyle }$)${\displaystyle }$( 1${\displaystyle }$- ${\displaystyle 2}$ ${\displaystyle \mathrm{m}}$) ${\displaystyle f(m)=m(1-m)(1-2$ m$)}$에 대해 얻은 곡선을 적합시켜 약 99%까지 근사치를 구할 수 있다$.$오류는 더 큰 루트에 대해 빠르게 증가하며, 이에 대해 Barbour는 방법이 $부적절$하다고 생각했다. 오류 곡선은 f(${\displaystyle x}$)${\displaystyle }$= x${\displaystyle (1}$- ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle a^{}}$ )${\$ 형식과 유사하며$$, N이 증가함에 따라 m=1에 더 가까워진다.

쇤베르크의 바르보르의 수법 개량

이 논문은 주심인 아이작 제이콥 쇤베르크에 의해 추가된 두 개의 노트로 출판되었다.그는 바버가 도출한 공식은 분수 선형 변환이며, 그래서 관점을 요구하는 것이며, 두 라인의 해당 지점의 세 쌍이 특이하게 투영적인 대응 바버의 조건을 결정했기 때문에 OA가 QR에 수직이라는 것은 무관하다고 보았다.이 단계를 생략하면 QR의 길이를 보다 편리하게 선택할 수 있고, 작업 횟수를 줄일 수 있다.

쇤베르크는 1976년 미국 수학 월간지에 게재된 "기타에 대한 초조함의 위치에 대하여"라는 짧은 논문에서 확장된 바보어의 방정식은 3점 m=0, m=1/2, m=1을 통한 지수 곡선의 보간으로 볼 수 있다고도 언급했다.^[22]$본{\displaystyle \sqrt{\mathrm{}}}$ 기사는 스트롤이 반옥타브에 ${\displaystyle \frac{41}{}}$ ${\displaystyle \frac{29}{}}$ ${\$$displaystyle \scriptstyle {\frac{$411}{$29$$}}}$을(를$)$ 우연한 방법으로 사용한 것에 대한 간략한 토론으로 끝을 맺었다$.$분모의 Ize

스튜어트 및 계속 분수

Stråhle의 $건축$에서 2 ${\${\$sqrt{2}}:}$의 부분 근사치 사용은 이안 스튜어트에 의해 확장되었다. 그는 1992년 저서 "A Well Calmulated Calculator"에서 "A Well"의 시공에 대해 썼다.^[23] 2006년에 출판된 음악과 수학에 포함된 "Faggot's Faitful Fiasco"뿐만 아니라 "Faggot's Faucleful Fiasca"도 포함되어 있다.스튜어트는 투영 기하학의 관점에서 건설을 고려했고, $처음$부터 y${\displaystyle }$=${\displaystyle \frac{}{}}$( x${\displaystyle \frac{}{}}$+ b${\displaystyle \frac{}{}}$)${\displaystyle \frac{}{}}$(${\displaystyle \frac{c}{}}$+ ${\displaystyle \frac{d}{}}$) ${\$ 형식의 부분 선형 함수로 처리하여 Barbour와 동일한 공식을 도출해 냈으며$,$ 이에 대한 근사치를 지적했다.${\displaystyle \sqrt{}}$구성에 ${\displaystyle \sqrt{\mathrm{포함}}}$된$$2 {\$displaystyle \scriptstyle${\$sqrt{2}}$는 17 ${\displaystyle \frac{12}{}}$ ${\$이며$,$ 이는 이 구조가 생성하는 반 옥타브에서 다음으로 낮은 수렴이다.이는 m=0.5에$$ $대해{\displaystyle \frac{\mathrm{p}}{}}$ + 2 ${\displaystyle \frac{}{}}$ p${\displaystyle \frac{}{}}$+ q + ${\displaystyle \frac{q}{}}${\$displaystyle \scriptstyle {\p+2q}{p$+q$}}}$로 단순화하는 기능의 결과로서 p ${\displaystyle \frac{q}{}}$ ${\$은 생성$$ 근사이다.

악기에 적용되는 유사한 방법

바버가 편찬한 악기 초안판뿐만 아니라 모노코드를 나누는 기하학적 방법과 산술적 방법은 각각이 나타내거나 내포하고 있는 서로 다른 곡조를 묘사하기 위한 명시적인 목적이었으며 쇤베르크와 스튜어트의 작품들은 비슷한 초점과 참고 문헌을 간직하고 있었다.피아노 건축에 포함되지 않은 세 권의 교과서는 새로운 악기를 설계하기 위한 스트롤의 것과 유사한 구조를 보여주지만 그들의 음의 튜닝을 독립적으로 다룬다; 두 건축물은 바버어의 "숫자의 뿌리에 대한 기하학적 근사"에서 쇤베르크의 관찰에 의해 제안된 바와 같이 수직이 아닌 형태를 취하고 있다.d 하나는 최적의 결과를 얻는 반면 다른 하나는 2가 아닌 루트를 가진 응용 프로그램을 보여준다.

쿠칭 시

19세기 중반 베른의 오르간과 피아노 제작자인 칼 쾨징은 1833년부터 피아노 디자인에 관한 그의 첫 번째 책인 '이론티슈 프라키츠'에서 발행물에 기술된 여러 가지 기하학적 구조를 읽고 옥타브에서 소리 길이를 결정하는 간단한 방법을 고안했다고 썼다.마르푸르의 역사-염병학(Historisch-kolitch-kinschen Beitragen jur Aufnahme der Mussik)의 e; 그는 이 사단이 매우 정확할 것이며 이 공사가 초조해 하는 기타에 사용될 수 있다고 말했다.

쿠칭은 같은 목적으로 만들어질 대규모 부문을 설명한 후 이 공사를 도입했다.그는 11년 후에 출판된 Das Wissenschaftliche der Fortepiano-Baukunst에 어떤 방법도 포함하지 않았다. 여기서 그는 옥타브 길이 사이의 약 18:35 비율을 사용하여 길이를 계산했고, 장력 점프의 톤 차이를 줄이기 위해 실제 와이어 직경에 대해 조정된 비연속 곡선으로 새로운 방법을 제안했다.^[24]

Kützing은 알려진 소리 길이를 나타내는 선분할 ba에 45도, 그리고 b와 c 사이의 중간에 위치한 d 지점의 옥타브에서 e에서 교차하는 ba에 수직으로 선을 확장한 다음 d를 12개의 동일한 부분으로 나누도록 지시하였다.a on ab 지점은 b로부터 e로부터 de, db, 그리고 b로부터 de를 나누고 bc를 교차하는 지점까지 확장된 광선을 전달하여 c로부터 문자열 길이의 다른 끝점을 찾는다.^[25]

이 배열은 a를 찾기 위해 평균 비례를 사용하는 것과 같다.

지침서에 Are-labeled도 팜플렛 영국 최대의 피아노 제조 업체 존 Broadwood 및에 의해 인쇄된에서, 아들이 1862년 국제 박람회 런던에 머무르고 있는 천의 길이를 발견하는 것의 옥타브의 평균율에 모든 음에 대한 현실적인 방법,"라고 표현했다;s그들과 동행하도록 포함시켰다.월 OOO동일한 크기의 와이어로 각 노트의 장력은 동일해야 한다."^[26]

그것은 또한 나폴리에서 일하는 러시아 태생의 피아노 제작자인 Giacomo Siebers에 의해 1868년 저서 Il Pianoforte에서 부문과 함께 복제되었다. 그곳에서 그는 그것이 피아노에서 현악의 소리 길이를 결정하는 가장 실용적인 방법이라고 주장했다.브로드우드처럼, 시버스는 그것의 출처나 사용 범위를 설명하지 않았고, 그 이면에 있는 어떤 이론도 설명하지 않았다.그는 또한 그것이 피아노 디자인 이상의 어떤 쓸모가 있다고 제안하지 않았다.^[27]

울펜던

영국의 피아노 제작자 사무엘 울펜든은 1916년에 출판된 '피아노포르테 건축술에 관한 논문'에서 피아노에서 가장 낮은 소리 나는 평범한 줄의 길이를 제외한 모든 길이를 결정하는 건축물을 제시했다. 그는 시버스와 마찬가지로 이것이 독창적인 절차인지 일반적인 절차인지에 대해서는 설명하지 않고 "매우 실용적인 방법"이라고만 말했다.끈 길이를 결정하는 풍습이 있었고, 지난 몇 년 동안 나는 그것을 모두 사용했다."그는 글을 쓸 당시 길이 계산이 "어느 정도 더 쉽다"는 것을 직접 발견했으며, 피아노의 상위 5 옥타브에 대한 계산된 길이 표를 가지고 설명에 앞서 있었다고 덧붙였다.^[28]그는 같은 기질에 주파수를 포함시켰지만, 1927년 부록에 청각적 튜닝 지침만 발표했다.

울펜덴 명시적으로 자신을 범위에 달성하기 위해 문자열 직경에 contras을 변화( 그렇지 않으면 비슷한 시스템 지크프리트 Hansing가 출판에 1888[29]은 약간 더 지속적인 결과들을 달성하기)과 옥타브 길이 사이의 9:17비를 접목시키자고 건의한 것은 명백한 문자열의 긴장을 동등한 것을 주장했다.에 t더 굵고 낮은 사운딩 피치의 경우 스트링 스케줄이 더 높은 장력을 초래하는 시버 스케일.

시버스와 마찬가지로 울펜덴은 상위 지점으로부터 54, 102, 192.5, 364, 688mm로 설계한 범위에서 각 C에 대해 위치한 점을 시작으로 광선의 베이스 라인에서 45도 떨어진 단일 세그먼트에 모든 음향 길이를 구성했다.광선의 정점 4개는 각 옥타브의 하단 C에서 확장된 수평 베이스 라인의 교차점에 의해 위치하지만, 두 번째 라인은 기본 라인에 대해 51.5도 각도가 되어야 하며 기본 라인은 차이와 함께 35:13의 비율을 가져야 한다고 그가 지정했다.두 옥타브 길이 사이의 빛

울펜덴의 방법은 대략 1.${\displaystyle \sqrt{3775}}$로 ${\displaystyle \sqrt{17}}$${\displaystyle \sqrt{}}$/ 9 ${\$에 가깝고, 바버 형태의$$ ${\displaystyle \mathrm{OA}\mathrm{/OB}}$ = 8$.$ ${\$이것은 작은 옥타브를 보상하면 596 센트의 반 옥타브를 생성하는데, 그의 계산된 수치와 비교했을 때 F4(f³)에서 약 1mm의 오차가 발생한다.

메모들

• ^a Stråhle(1743) 페이지 285-286:

"Enligit detta påfund, har jag bygt et Monochordium, i så måtto, at det fullan hafver 13 strängar, ock skulle dy snarare heta Tredekachordium, men som alla strängarna, äro af en nummer, längd ock thon ; så behåller jag det gamla namnet.

"Til dessa tretton strängar, är lämpadt et vanligit Manual, af en Octave; men under hvar sträng, sedan de noga äro stämde i unison, sätter jag löfa stallar, å de puncter, ock till de längder fra crepinerne, som min nu beskrefne Linea Musica det äfkar : derefter hvar sträng undfår sin behöriga thon.

"Det Claver, som jag här til förfärdigat är jämnväl i de tre högre Octaverne, noga rättadt efter min Linea Musica, til strängarnes längd ock skilnad : ock på det stämningen, må utan besvär, kunna ske ; så är mit Monochordium så giordt, at det kan ställas ofvan på Claveret, då en Octav på Claveret stämmes, thon för thon, mot sina tillhöriga thoner på 모노코르디움, 부랑자 알라 데 앤드라 토네르네, å 클라베레, 스테마스 옥타브스-비스; 데닝겐, 베르크스트텔라, 에메단 덴 var르 ö르 sv트닝가르."

• ^b Faggot(1743) 페이지 286:

  "Huruvida thonernes stämning, efter förut beskrefne Påfund, förnöger hörsten, med behageligare ljud, ock med bättre likstämmighet, i de Musikaliska thonerne å et Claver, än de gamla ock härtils bekanta stämnings sätt, derom lärer förståndet bättre kunna döma, när ögat får se det örat hörer."

• ^ Marpurg (1776) 페이지 167-168:

  "Ich muss gessehen, dass sich dieer Aufsatz mit Vergnügen lesen lésset, und dass ich von der Richtigkeit der der hrn을 토해낸다.제이콥 파그고, 더치 아인 뮌헨 트리오노메트리스체 베레흐농 더 스트렐리스첸 리니엔, 게펀든 자일렌 볼리그 뷔르체게트 빈.Nur muss ich ich hinzufügen, dass die gefunden Zahlen nicht geben, sie geben sollen, und Hr.Stréhle thatte, nemlich eine Temperature, welche das Schweben am gelindesten für das Gehör macht, und allea Töne in Gehörige Gleichst 이민자 세트.에스엔탈렌 넬리히 니콜라이츠 안데르스 아인 언글리히슈켄드 템퍼레이터, 언트니크 아인말 폰 데어 에르트르글리히스텐 아트."

참조

• 다니엘 P.Stråle "Nyt Påfund, finna Tempern I stémningen, för thonne, å Claveret ock dylika Instrumenter" Kongigy Swenska Wetenskaps Academiciens Handlingar För Madern, volumber, o.IV, 로렌츠 루드비히 그레핑, 스톡홀름 1743 페이지 281-285
• Jacob Faggot "Trigonomethisk utrékning p en ny Thermatur, för thonernes stémning ning Claveret" 콩리가 스웬스카 Wetenskaps Academiciens Handlingar för Månaderne 10월, 11월 volck.IV, 로렌츠 루드비히 그레핑, 스톡홀름 1743 페이지 286-291
• 이언 스튜어트 "Faggot's Faudful Fiasco" 존 포벨, 레이먼드 플러드, 로빈 윌슨, 에드.음악과 수학 옥스퍼드 대학 출판 2006 페이지 68-75
• J. 머레이 바버 튜닝과 기질: 역사 조사 미시건 주립대학 출판부, 1951 페이지 65-68