렌더링 방정식

렌더링 방정식은 들어오는 빛과 BRDF에 대한 함수가 주어진 특정 시야 방향을 따라 점 x에서 방출되는 빛의 총량을 설명한다.

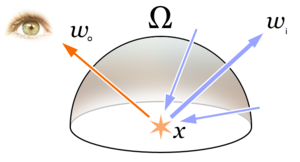
컴퓨터 그래픽에서, 렌더링 방정식은 한 점을 떠나는 평형 광도 조도가 기하학적 광학 근사치 아래 방출된 플러스 반사 광도의 합으로 주어지는 적분 방정식이다. 1986년 데이비드 이멜 외 ^[1]연구원과 제임스 카지야에^[2] 의해 동시에 컴퓨터 그래픽에 도입되었다. 컴퓨터 그래픽의 다양한 사실적인 렌더링 기법들은 이 방정식을 해결하려고 시도한다.

렌더링 방정식의 물리적 근거는 에너지 보존의 법칙이다. L이 광채를 나타낸다고 가정하면, 각 특정 위치와 방향에서 나가는 빛(L_o)은 방출되는 빛(L_e)과 반사된 빛의 합이다. 반사광 자체는 입사광(L_i)의 모든 방향에서 입사각의 표면반사와 코사인(cosine)을 곱한 합이다.

방정식형식

렌더링 방정식은 양식으로 작성할 수 있다.

L_{\text{o}(\mathbf {x},\omega_{\text{o},\lambda ,t)=L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)\ +\int _{\Omega }f_{\text{r}}(\mathbf {x} ,\omega _{\text{i}},\omega _{\text{o}},\lambda ,t)L_{\text{i}}(\mathbf {x} ,\omega _{\text{i}},\lambda ,t)(\omega _{\text{i}}\cdot \mathbf {n} )\operatorname {d} \omega _{\text{i}}

어디에

$L_{\text{o}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ is the total spectral radiance of wavelength $\lambda$ directed outward along direction $\omega _{\text{o}}$ at time $t$ , from a particular position $\mathbf {x}$ $\mathbf {x}$
$\mathbf {x}$ ${\$ 이 $\mathbf {x}$ $($ 가) 공간 내 위치
$\omega _{\text{o}}$ $\omega _{\text{o}}$ ${\$ 은 $\omega _{{{\text{o}}}}$ (는) 나가는 빛의 방향이다.
$\lambda$ $\lambda$ 은 $\lambda$ (는) 빛의 특정 파장이다.
$t$ $[\displaystyle t}$ 은 $t$ (는) 시간임
$L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ ( $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ , $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ , $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ , $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ ) $L_{\text{e}(\mathbf {x}),\omega _{\text{o},\lambda ,t)$ 이(가) 스펙트럼 광도를 방출한다 $L_{\text{e}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ .
$\int _{\Omega }\dots \operatorname {d} \omega _{\text{i}}$ $\int _{\Omega }\dots \operatorname {d} \omega _{\text{i}}$ … $\int _{\Omega }\dots \operatorname {d} \omega _{\text{i}}$ i ${\$ {\ $text{$ i}}}}은 $\int _{\Omega }\dots \operatorname {d} \omega _{\text{i}}$ (는 $)$ $\Omega$ {\ $displaysty \Oomega }$ 에 대한 정수임.
$\Omega$ $\Oomega$ 은 $\Omega$ (는) $\mathbf {n}$ ${\$ 을(를) 중심으로 하는 단위 반구로, $\omega _{\text{i}}$ $\omega _{\text{i}}$ ${\$ 에 대해 가능한 모든 값이 포함되어 $\mathbf {n}$ 있다.
$f_{\text{r}}(\mathbf {x} ,\omega _{\text{i}},\omega _{\text{o}},\lambda ,t)$ is the bidirectional reflectance distribution function, the proportion of light reflected from $\omega _{\text{i}}$ to $\omega _{\text{o}}$ at position $\mathbf {x}$ ${\$ $시간$ t ${\displaystyle t$ 파장 $\lambda$ $\lambda$
$\omega _{\text{i}}$ $\omega _{\text{i}}$ ${\$ 는 $\omega _{\text{i}}$ 들어오는 빛의 음 방향이다.
$L_{\text{i}}(\mathbf {x} ,\omega _{\text{i}},\lambda ,t)$ is spectral radiance of wavelength $\lambda$ coming inward toward $\mathbf {x}$ from direction $\omega _{\text{i}}$ at time $t$
$\mathbf {n}$ ${\$ 은 $($ 는) x ${\$ 에서 표면 정규 분포임 $\mathbf {n}$
$\omega _{\text{i}}\cdot \mathbf {n}$ $\omega _{\text{i}}\cdot \mathbf {n}$ $\omega _{\text{i}}\cdot \mathbf {n}$ ${\$ 은 광속이 광선에 수직으로 돌출된 면적보다 큰 표면을 가로질러 가리기 때문에 입사 각도로 인한 외부 일조도의 약화 요인이다 $\omega _{\text{i}}\cdot \mathbf {n}$ . 이것은 종종 $\cos \theta _{i}$ $\cos \theta _{i}$ $\cos \theta _{i}$ ${\$ 라고 쓰여진다 $\cos \theta _{i}$

두 가지 주목할 만한 특징은 선형성(승수와 추가만으로 구성됨)과 공간적 동질성(모든 위치와 방향에서 동일함)이다. 이것은 방정식의 광범위한 요소와 재배열이 가능하다는 것을 의미한다. 양자장 이론에서 발생하는 것과 비슷한 제2종 프레드홀름 적분 방정식이다.^[3]

이 방정식의 스펙트럼 및 시간 의존성에 유의하십시오. $L_{\text{o}}$ $L_{\text{o}}$ ${\$ 은(는) 3색 컬러 샘플을 얻기 위해 가시 스펙트럼의 섹션에 걸쳐 샘플링하거나 통합될 수 있다 $L_{\text{o}}$ . 애니메이션의 단일 프레임에 대한 픽셀 값은 $고정$ t $;$ $t;$ 모션 $t;$ 블러드는 일정한 시간 간격에 걸쳐 $L_{\text{o}}$ 평균 $L_{\text{o}}$ $L_{\text{o}}$ ${\\$ 을(시간 간격에 걸쳐 통합하고 간격의 길이로 나누면) 생성될 수 있다.^[4]

렌더링 방정식의 해결책은 함수 $L_{\text{o}}$ $L_{\text{o}}$ ${\$ 입니다 $L_{\text{o}}$ $L_{\text{i}}$ $L_{\text{i}}$ ${\$ 함수는 다음 레이트레이싱 작업을 $L_{\text{o}}$ $L_{\text{o}}$ L $L_{\text{o}}$ {\ $displaystyle$ L_{\ $text{o}}$ 과(와) 관련이 있다 $L_{\text{i}}$ . 한 지점에서 어떤 방향에서 들어오는 광도는 반대 방향의 어떤 다른 지점에서 나가는 광도다.

적용들

주어진 씬(scene)에 대한 렌더링 방정식을 해결하는 것이 현실적인 렌더링에서 가장 큰 과제다. 방정식을 해결하기 위한 한 가지 접근방식은 유한요소법에 기초하여 방사성 알고리즘으로 이어진다. 몬테카를로 방법을 사용한 또 다른 접근방식은 경로 추적, 광자 매핑, 메트로폴리스 광수송을 포함한 많은 다른 알고리즘을 가져왔다.

제한 사항

이 방정식은 매우 일반적이지만, 빛 반사의 모든 측면을 포착하지는 않는다. 누락된 측면은 다음과 같다.

유리 물체나 수면에 부딪힐 때와 같이 빛이 표면을 통해 전달될 때 발생하는 전송,
들어오는 빛과 나가는 빛의 공간 위치가 다른 표면 아래 산란. 표면 아래 산란을 고려하지 않고 렌더링한 표면은 자연적으로 불투명하게 보일 수 있지만, 전송이 방정식에 포함된 경우 표면 아래에 산란된 빛도 효과적으로 포함되기 때문에 이를 설명할 필요는 없다.
양극화, 예를 들어 빛이 수면에서 반사되는 경우와 같이 서로 다른 광선 편광 분포를 갖는 경우
인광, 광선이나 다른 전자기 방사선이 한 순간에 흡수되어 후기에 방출될 때 발생하는 것으로, 보통 파장이 더 길다(흡수된 전자파 방사선이 매우 강렬하지 않는 한),
간섭, 빛의 파동 특성이 나타나는 경우
흡수된 빛과 방출된 빛이 다른 파장을 갖는 형광,
매우 강렬한 빛이 단일 광자보다 더 많은 에너지를 가진 전자의 에너지 수준을 증가시킬 수 있는 비선형 효과(전자가 두 광자를 동시에 맞으면 이러한 현상이 일어날 수 있음)와 표면에 부딪히는 빛의 주파수보다 더 높은 주파수의 빛의 방출이 갑자기 가능해지며, 또한 이러한 현상이 일어나게 된다.
상대론적 도플러 효과(상대론적 도플러 효과)는 매우 빠른 속도로 움직이는 물체에 반사되는 빛이 파장을 바꾸게 되는데, 빛이 그쪽으로 움직이는 물체에 반사되면 그 충격은 광자를 압축하게 되므로 파장이 짧아지고 빛이 블루스히프되어 광자가 더욱 촘촘하게 채워지게 된다. 그래서 광자 플럭스는 증가할 것이다; 만약 그것이 그것으로부터 멀어지는 물체에 튀면, 그것은 빨갛게 될 것이고 광자 플럭스는 더 희박하게 포장되어 광자 플럭스가 줄어들 것이다.

진공에서 단순한 표면으로 구성되지 않거나 빛의 이동 시간이 중요한 요소인 장면의 경우, 연구자들은 볼륨 렌더링에 적합한 볼륨 렌더링 방정식과 비행 시간 카메라의^[5] 데이터와 함께 사용할 수 있는 과도 렌더링 방정식을 만들기 위해 렌더링^[6] 방정식을 일반화했다.

참조

^ Immel, David S.; Cohen, Michael F.; Greenberg, Donald P. (1986), "A radiosity method for non-diffuse environments" (PDF), SIGGRAPH 1986: 133, doi:10.1145/15922.15901, ISBN 978-0-89791-196-2
^ Kajiya, James T. (1986), "The rendering equation" (PDF), SIGGRAPH 1986: 143–150, doi:10.1145/15922.15902, ISBN 978-0-89791-196-2
^ Watt, Alan; Watt, Mark (1992). "12.2.1 The path tracing solution to the rendering equation". Advanced Animation and Rendering Techniques: Theory and Practice. Addison-Wesley Professional. p. 293. ISBN 978-0-201-54412-1.
^ Owen, Scott (September 5, 1999). "Reflection: Theory and Mathematical Formulation". Retrieved 2008-06-22.
^ Kajiya, James T.; Von Herzen, Brian P. (1984), "Ray tracing volume densities", SIGGRAPH 1984, 18 (3): 165, CiteSeerX 10.1.1.128.3394, doi:10.1145/964965.808594
^ Smith, Adam M.; Skorupski, James; Davis, James (2008). Transient Rendering (PDF) (Technical report). UC Santa Cruz. UCSC-SOE-08-26.

외부 링크

Stanford University 과정 CS 348B, Computer Graphics의 강의 노트: 이미지 합성 기법

[1] Immel, David S.; Cohen, Michael F.; Greenberg, Donald P. (1986), "A radiosity method for non-diffuse environments" (PDF), SIGGRAPH 1986: 133, doi:10.1145/15922.15901, ISBN 978-0-89791-196-2

[2] Kajiya, James T. (1986), "The rendering equation" (PDF), SIGGRAPH 1986: 143–150, doi:10.1145/15922.15902, ISBN 978-0-89791-196-2

[3] Watt, Alan; Watt, Mark (1992). "12.2.1 The path tracing solution to the rendering equation". Advanced Animation and Rendering Techniques: Theory and Practice. Addison-Wesley Professional. p. 293. ISBN 978-0-201-54412-1.

[4] Owen, Scott (September 5, 1999). "Reflection: Theory and Mathematical Formulation". Retrieved 2008-06-22.

[5] Kajiya, James T.; Von Herzen, Brian P. (1984), "Ray tracing volume densities", SIGGRAPH 1984, 18 (3): 165, CiteSeerX 10.1.1.128.3394, doi:10.1145/964965.808594

[6] Smith, Adam M.; Skorupski, James; Davis, James (2008). Transient Rendering (PDF) (Technical report). UC Santa Cruz. UCSC-SOE-08-26.

[1]

[2]

[3]

[4]

[5]

[6]

Search

렌더링 방정식

네임스페이스

더

목차

방정식형식

적용들

제한 사항

참조

외부 링크