광탄성

광탄성(photo elasticity)은 기계적 변형에 따른 재료의 광학적 특성 변화를 설명한다.이것은 모든 유전 매체의 특성이며 종종 재료의 응력 분포를 실험적으로 결정하는 데 사용되며, 재료의 불연속성 주변의 응력 분포를 묘사합니다.광탄성 실험(비공식적으로 광탄성이라고도 함)은 재료의 중요한 응력점을 결정하는 중요한 도구이며 불규칙한 기하학적 구조의 응력 집중도를 결정하는 데 사용된다.

역사

이 광탄성 현상은 스코틀랜드 물리학자 데이비드 브루스터에 의해 처음 발견되었는데, 그는 즉시 이 현상을 스트레스로 인한 ^[1][2]복굴절이라고 인정했다.그 진단은 오거스틴-진 ^[3]프레넬의 직접 굴절 실험에서 확인되었다.실험적인 틀은 런던 대학의 E. G. Coker와 L. N. G. Filon의 연구로 20세기 초에 개발되었다.1930년 캠브리지 프레스에서 출판된 그들의 책 '광탄성 논문'은 이 주제에 대한 표준 텍스트가 되었다.1930년에서 1940년 사이에, 러시아어, 독일어, 프랑스어로 된 책을 포함하여, 이 주제에 관한 많은 다른 책들이 출판되었다.Max M. Frocht는 현장에서 ^[4]고전적인 두 권의 작품인 광탄성(photo elasticity)을 출판했습니다.동시에, 이 분야에서는 많은 발전이 이루어졌습니다.기법이 크게 향상되어 기기의 심플화가 이루어졌습니다.기술이 개선됨에 따라, 광탄성 실험은 3차원 응력 상태를 결정하는 데까지 확장되었습니다.실험 기술 발전에 병행하여 편광 탄성학의 첫번째 현상학적 설명 1890년에 프리드리히 Pockels,[5]에 의해 하지만 이런 부적절한 거의 1세기 뒤 넬슨 및에 의해 증명되었다;Lax[6]Pockels의 설명으로는 단지 기계적인 스트레인의 엄마의 광학적 성질에 미치는 영향은 고려했다 받았다.terial.

디지털 폴라스코프의 등장으로 (발광 다이오드로 가능) 부하가 걸린 구조물에 대한 지속적인 모니터링이 가능해졌다.이는 동적 광탄성의 발달로 이어져 재료의 파괴와 같은 복잡한 현상 연구에 크게 기여하였다.

적용들

광탄성성은 특히 유한 요소나 경계 요소와 ^[7]같은 수치 방법이 등장하기 전에 다양한 응력 분석 및 설계에서의 일상적인 사용에 사용되어 왔다.폴라리스코피의 디지털화를 통해 빠른 이미지 취득과 데이터 처리가 가능해져 산업용 응용 프로그램이 유리, ^[9]폴리머 등의 재료^[8] 제조 공정 품질을 제어할 수 있습니다.치과에서는 광탄성을 이용하여 틀니 ^[10]소재의 변형을 분석합니다.

광탄성(photo elastability)은 석조 구조물^[11][12][13] 내 또는 탄성 ^[14]매체에 내장된 강직선 포함물(스티퍼너)에 근접하여 고도로 국소화된 응력 상태를 조사하기 위해 성공적으로 사용될 수 있습니다.전자의 경우 벽돌 사이의 접촉으로 인해 문제가 비선형적인 반면 후자의 경우 탄성 용액이 특이하므로 수치적 방법이 정확한 결과를 제공하지 못할 수 있다.이것들은 광탄성 기술을 통해 얻을 수 있다.고속 촬영과 통합된 동적 광탄성을 이용하여 ^[15]재료의 파괴 거동을 조사한다.광탄성 실험의 또 다른 중요한 적용은 이중 재료 ^[16]노치 주변의 응력장을 연구하는 것이다.이중 재료 노치는 용접 또는 접착 접합 구조물과 같은 많은 엔지니어링 애플리케이션에 존재합니다.

형식적 정의

선형 유전체 재료의 변형에 대한 역 유전율 텐서${\displaystyle }\delta {\displaystyle \mathrm{}}$(${\displaystyle {\theta }_{}}$ ${\displaystyle {-}^{}{}_{}{1}^{}}$) i $(\$^{-$1})_{ij})$의 변화(변위${\displaystyle {\mathrm{}}_{}}$δ ${\displaystyle u_{}}$ k$\displaystyle$ \$partial$ _${\ell }_k$는 다음과 같다.

$\displaystyle \Delta (\varepsilon ^{-1}_{ij}=P_{ijk\ell}\partial_{k}u_{\ell}}$

$여기$서 ${\displaystyle {\mathrm{Pi}}_{}}$ ${\displaystyle j_{}}$ ${\displaystyle k_{}}$ ${\$ { $display style$ P _ { $ijk$\ $ell }$ $is$ 4 $랭크$ 광탄성 텐서, u ${\$ { \ displaystyle$$$u$_ { \ $ell$} is$$ l$$\ $displaystyle x _$$${ $l$$\}\}$${\displaystyle {\mathrm{}}_l}$ r r r r r r r r r where where where where where where $where{\displaystyle {}_{}}$ ${\displaystyle {where}_{}}$ where where where where where where where where where where where where where where where where where where whereopic materials, 이 정의는 다음과 같이 단순해집니다.

$\displaystyle \Delta (\varepsilon ^{-1})_{ij}=p_{ijk\ell}s_{k\ell}}$

${\displaystyle {여기}_{}}$서 p ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\displaystyle k_{}}$ ${\$ { $displaystyle p_{ijk\ell }}$는 광탄성 텐서(광탄성 변형 텐서)의 대칭 $부분$이고 ${\displaystyle s_{}}$ ${\displaystyle k_{}}$ ${\$ { $displaystyle s_{k$\ell$$}}는$$ 선형 변형률입니다.${\displaystyle {\mathrm{Pi}}_{}}$ j ${\displaystyle k_{}}$ ${\$ { $displaystyle P_{ijk\ell$}}의 반대칭 부분은 회전 광학 텐서로 알려져 있습니다.어느 정의에서든 신체에 대한 변형이 광학 이방성을 유도할 수 있으며, 광학적으로 등방성 물질이 복굴절을 나타낼 수 있다.대칭 광탄성 텐서는 기계적 스트레인에 관해 가장 일반적으로 정의되지만, 기계적 응력의 관점에서 광탄성을 표현할 수도 있다.

실험 원리

실험 절차는 특정 투명 재료에 의해 나타나는 복굴절의 특성에 의존합니다.복굴절은 주어진 물질을 통과하는 광선이 두 가지 굴절률을 보이는 현상이다.복굴절(또는 이중 굴절)의 특성은 많은 광학 결정에서 관찰됩니다.응력을 적용하면 광탄성 재료는 복굴절의 특성을 나타내며 재료의 각 지점에서 굴절률의 크기는 해당 지점의 응력 상태와 직접 관련이 있다.폴라스코프라고 불리는 기기로 복굴절률을 분석함으로써 최대 전단 응력과 방향 등의 정보를 얻을 수 있습니다.

빛이 광탄성 물질을 통과할 때 전자파 성분이 두 가지 주요 응력 방향을 따라 분해되고 각 성분이 복굴절률로 인해 다른 굴절률을 경험합니다.굴절률의 차이는 두 구성 요소 간의 상대적 위상 지연으로 이어집니다.2차원 광탄성이 적용 가능한 등방성 재료로 만들어진 얇은 시료를 가정할 때 상대 지연의 크기는 응력 광학 ^[19]법칙에 의해 주어진다.

${\displaystyle \Delta = pi t}{\sigma }C(\sigma _{1}-\sigma _{2})}$

여기서 δ는 유도지연, C는 응력광학계수, t는 시료두께, θ는₁ 진공파장, θ는₂ 제1 및 제2의 주요응력이다.지연은 투과된 빛의 편광을 변화시킵니다.편광경은 시료를 통과하기 전과 통과 후의 광파 편광 상태를 합친 것이다.두 파형의 광학적 간섭에 의해 프린지 패턴이 드러난다.프린지 순서 N의 수는 다음과 같이 표시됩니다.

${\displaystyle N=black{2\pi }}$

상대적인 지연에 따라 달라지죠프린지 패턴을 연구함으로써 재료의 여러 지점에서 응력 상태를 파악할 수 있습니다.

광탄성 거동을 보이지 않는 재료의 경우에도 응력 분포를 연구할 수 있습니다.첫 번째 단계는 조사 중인 실제 구조와 유사한 형상을 가진 광탄성 재료를 사용하여 모형을 만드는 것입니다.그런 다음 모델의 응력 분포가 실제 구조의 응력과 유사하도록 동일한 방식으로 하중을 적용합니다.

등색학과 등색학

등사선은 주요 응력이 동일한 방향으로 있는 표본 내 점의 위치이다.

등색학은 첫 번째와 두 번째 주요 응력의 차이가 동일하게 유지되는 점들의 위치이다.따라서 이러한 선은 최대 전단 응력 크기가 동일한 ^[20]점을 연결하는 선입니다.

2차원 광탄성

광탄성은 스트레스의 3차원 상태와 2차원 상태를 모두 설명할 수 있다.그러나 3차원 시스템에서 광탄성을 검사하는 것은 2차원 또는 평면 응력 시스템보다 더 관련이 있다.그래서 이번 섹션에서는 평면 응력 시스템의 광탄성(photo elastability)에 대해 설명합니다.이 조건은 프로토타입의 두께가 평면 치수에 비해 훨씬 작을 때 달성됩니다.따라서 다른 응력 성분은 0이므로 모델의 평면에 평행하게 작용하는 응력만 고려됩니다.실험 설정은 실험마다 다릅니다.사용되는 설정에는 평면 폴라스코프와 원형 폴라스코프가 있습니다.

2차원 실험의 작동 원리는 첫 번째와 두 번째 주 응력과 그 방향의 차이로 변환될 수 있는 지연의 측정을 가능하게 한다.각 응력 성분의 값을 더 얻기 위해서는 응력 분리라는 기술이 필요합니다.^[21]개별 응력 성분을 해결하기 위한 추가 정보를 제공하기 위해 여러 이론 및 실험 방법이 사용됩니다.

평면 폴라스코프 설정

설정은 두 개의 선형 편광자와 광원으로 구성됩니다.이 광원은 실험에 따라 단색 빛 또는 백색 빛을 방출할 수 있다.우선 첫 번째 편광자는 빛을 평면 편광으로 변환하는 제1편광자를 통과시킨다.이 장치는 이 평면 편광은 응력 시료를 통과하도록 설치된다.이 빛은 시료의 각 지점에서 그 지점에서 주된 응력 방향을 따라간다.그런 다음 빛이 분석기를 통과하면 마침내 프린지 패턴을 얻을 수 있습니다.

평면 폴라스코프 설정의 프린지 패턴은 등색계와 등사정계로 구성됩니다.등각선은 편광경의 방향에 따라 변화하지만 등각색소에는 변화가 없습니다.

원형 편광경 설정

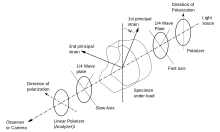
원형 편광경 설정에서는 2개의 1/4파 플레이트가 평면 편광경의 실험 설정에 추가됩니다.첫 번째 1/4파 플레이트는 편광자와 시료 사이에 배치하고 두 번째 1/4파 플레이트는 시료와 분석기 사이에 배치한다.소스 측 편광자 뒤에 1/4파 플레이트를 추가하면 원형 편광 빛이 샘플을 통과하게 됩니다.분석기 측 1/4파 플레이트는 빛이 분석기를 통과하기 전에 원형 편파 상태를 다시 선형으로 변환합니다.

평면 폴라스코프에 비해 원형 폴라스코프의 기본적인 장점은 원형 폴라스코프 설정에서는 등색성만 얻을 수 있고 등색성은 얻을 수 없다는 것입니다.이를 통해 등색체와 등색체를 구별하는 문제가 없어집니다.

「 」를 참조해 주세요.

• 음향 광학 변조기
• 전기 자극
• 기계 색채론
• 광탄성 변조기
• 편광 측정

레퍼런스

외부 링크

• 캠브리지 대학의 광탄성 페이지.
• 구조 및 광탄성 물리적 모델링 실험실(이탈리아 트렌토 대학교)
• 나만의 폴라스코프 제작