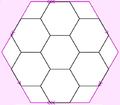
파푸스 그래프

파푸스 그래프
파푸스 그래프.
이름을 따서 명명됨	알렉산드리아 파푸스
정점	18
가장자리	27
반지름	4
지름	4
둘레	6
자동형성	216
색수	2
색도 지수	3
책두께	3
대기열 번호	2
특성.	양립자 대칭 거리-변환 거리-정규어 큐빅 해밀턴어
그래프 및 모수 표

그래프 이론의 수학적 분야에서 파푸스 그래프는 정점 18개와 가장자리 27개로 구성된 초당적 3정칙 비방향 그래프로서 파푸스 구성의 Levi 그래프로 형성된다.^[1] 파푸스 구성을 기술한 '헥사곤 정리'를 발견한 것으로 추정되는 고대 그리스 수학자 알렉산드리아의 파푸스의 이름을 따서 지은 것이다. 모든 세제곱 거리 정규 그래프는 알려져 있다; Pappus 그래프는 13개의 그래프 중 하나이다.^[2]

파푸스 그래프는 직선으로 교차하는 숫자 5를 가지며 교차 번호를 가진 가장 작은 입방 그래프다(OEIS에서 순서 A110507). 둘레 6, 지름 4, 반지름 4, 색채 번호 2, 색채 지수 3을 가지며 3번 버텍스 연결과 3번 에지 연결이다. 책 두께 3과 줄 2가 있다.^[3]

The Pappus graph has a chromatic polynomial equal to: ${\displaystyle (x-1)x(x^{16}-26x^{15}+325x^{14}-2600x^{13}+14950x^{12}-65762x^{11}+}$${\dis$$playstyle 229852x^{10}-653966x^{9}+1537363x^{8}-3008720x^{7}+4904386x^{6}-}$${\displaystyle 6609926x^{5}+7238770x^{4}-6236975x^{3}+3989074x^{2}-1690406x+356509)}$.

그 이름"Pappus 그래프"또한 관련nine-vertex graph,[4]에 Pappus 구성의 각 지점에 대한 꼭지점은, 같은 선에서 모든 쌍을 위한 가장자리에 참조하는 것이다. 이nine-vertex 그래프, 세 차갑삼각형 그래프의 노조의 보수 그래프, 그리고 완전히 3자 그래프 K3,3,6-regular은 사용되어 왔다.3. 첫 번째 파푸스 그래프를 토러스 안에 삽입하여 9개의 육각형 면으로 된 자기 페트리 이중 정규 지도를 만들 수 있고, 두 번째로는 18개의 삼각형 면으로 된 정규 지도를 만들 수 있다. 두 개의 일반 토로이드 지도가 서로 이중으로 되어 있다.

대수적 특성

파푸스 그래프의 자동형성 그룹은 순서 216의 그룹이다. 그것은 정점, 가장자리, 그리고 그래프의 호에서 전이적으로 작용한다. 따라서 파푸스 그래프는 대칭 그래프다. 그것은 어떤 정점과 어떤 가장자리로도 가져가는 자동모형을 가지고 있다. 포스터 인구조사에 따르면 F018A로 참조되는 파푸스 그래프는 18개의 정점에 대한 유일한 입방 대칭 그래프다.^[5][6]

파푸스 그래프의 특성 다항식은${\displaystyle }$( ${\displaystyle \mathrm{x}}$-${\displaystyle }$3 ) ${\displaystyle x}$ ${\displaystyle {4\mathrm{}}^{}}$( ${\displaystyle \mathrm{x}}$+ 3${\displaystyle }$) (${\displaystyle {x\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$- ${\displaystyle 3{}^{}}$) 6 ${\$)($x^{2}-3)^{6}$이며$,$ 이 특성 다항식을 가진 유일한 그래프로서 스펙트럼에 의해 결정된다.

갤러리

• 

  파푸스 그래프는 다양한 사이클을 강조하기 위해 색칠되었다.

• 

  파푸스 그래프의 색지수는 3이다.

• 

  파푸스 그래프의 색수는 2이다.

• 

  파푸스 그래프는 9개의 육각면이 있는 일반 지도로서 토러스 안에 내장되어 있다.

• 

  토러스 안에 포함된 파푸스 그래프와 관련 지도.

참조