n-11
n-vectorn-벡터 표현(geodetic normal 또는 타원체 normal vector라고도 함)은 수학적 계산과 컴퓨터 알고리즘에서 수평 위치 표현으로 위도와 경도를 대체하는데 적합한 3-모수 비성격 표현이다.
기하학적으로 타원체에서 주어진 위치에 대한 n-벡터는 타원체에서 그 위치에 정상인 바깥쪽 점의 단위 벡터다. 지구상의 수평 위치를 나타내기 위해 타원체는 기준 타원체이며 벡터는 지구 중심 지구 고정 좌표계로 분해된다. 그것은 모든 지구의 위치에서 원활하게 동작하며, 수학적 일대일 특성을 가지고 있다.
더 일반적으로, 이 개념은 경계가 다른 다지관이라면 k-차원 유클리드 공간의 엄격히 볼록한 부분 집합의 경계에 있는 위치를 나타내는 데 적용될 수 있다. 이 일반적인 경우, n-벡터는 k 매개변수로 구성된다.
일반 속성
엄격히 볼록한 표면으로의 정상 벡터는 표면 위치를 고유하게 정의하는데 사용될 수 있다. n-벡터는 단위 길이를 위치 표현으로 사용하는 바깥쪽 점의 정상 벡터다. [1]
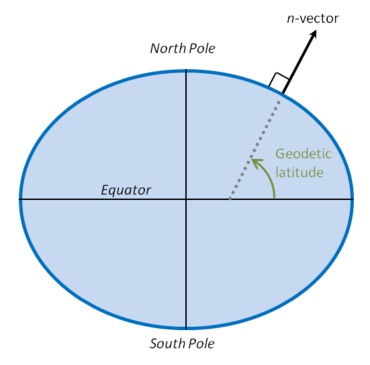
대부분의 용도에서 표면은 지구의 기준 타원체이므로 n-벡터는 수평 위치를 나타내기 위해 사용된다. 따라서 n-벡터와 적도면 사이의 각도는 그림에 나타낸 것과 같이 측지 위도에 해당한다.
표면 위치는 두 개의 자유도를 가지며, 따라서 두 개의 매개변수는 표면의 어떤 위치를 나타내기에 충분하다. 기준 타원체에서 위도 및 경도는 이 목적을 위한 공통 매개변수지만, 모든 2-모수 표현과 마찬가지로 특이점이 있다. 이는 자유도가 3도인 방향과 비슷하지만 3변수 표현은 모두 특이점이 있다.[2] 두 경우 모두 다른 매개변수를 추가하여 특이점을 피한다. 즉, 수평 위치를 나타내는 n-벡터(3개 매개변수)와 방향을 나타내는 단위 쿼터니온(4개 매개변수)을 사용한다.
n-multi는 일대일 표현으로, 어떤 표면 위치가 하나의 고유한 n-multi에 해당하고, 어떤 n-multi는 하나의 고유한 표면 위치에 해당한다는 것을 의미한다.
유클리드 3D 벡터로서 표준 3D 벡터 대수학을 위치 계산에 사용할 수 있으며, 이는 n-벡터를 대부분의 수평 위치 계산에 적합하게 만든다.
위도/경도를 n-벡터로 변환
e라고 불리는 ECEF 좌표계의 정의에 기초하여 위도/경도에서 n-벡터로 가는 것은 다음을 통해 달성된다는 것이 분명하다.
위첨자 e는 좌표계에서 n-벡터가 분해되는 것을 의미한다(즉, 첫 번째 구성요소는 e의 x축에 대한 n-벡터의 스칼라 투영이고, 두 번째 구성요소는 e의 y축에 대한 scalar 투영이다). 구형 및 타원형 지구 모델의 경우 방정식이 정확하다는 점에 유의하십시오.
n-벡터를 위도/경도로 변환
n-벡터, z 의 세 가지 성분에서 위도는 다음을 사용하여 확인할 수 있다.
가장 오른쪽 표현은 컴퓨터 프로그램 구현에 가장 적합하다.[1]
경도는 다음을 사용하여 찾을 수 있다.
이러한 표현식에서 (/ ) 은 atan2(y,x)에 대한 호출을 사용하여 구현되어야 한다. atan2(0,0)가 정의되지 않았기 때문에 경도의 극 특이도는 명백하다. 구형 및 타원형 지구 모델의 경우 방정식이 정확하다는 점에 유의하십시오.
예: 원 거리 큼
두 수평 위치 사이의 원 거리(구형 지구로 가정)를 찾는 것은 보통 위도와 경도를 이용하여 이루어진다. 이 거리에 대한 세 가지 다른 표현이 공통적이다; 첫째는 아크코, 둘째는 아크신, 마지막은 아크탄에 기초한다. 수학적 불안정을 피하기 위해 연속적으로 더 복잡한 표현은 찾기 쉽지 않고, 위도와 경도를 바탕으로 하기 때문에 극 특이점들이 문제가 될 수도 있다. 또한 위도와 경도의 델타도 포함하며, 일반적으로 ±180° 자오선과 극지방 근처에 주의하여 사용해야 한다.
벡터 대수 사용 가능성 때문에 n-벡터를 사용하여 같은 문제를 푸는 것이 더 간단하다. 아크코 표현은 도트 제품에서 얻어지는 반면 교차 제품의 크기는 아크신 표현을 준다. 이 둘을 합치면 아크탄 표현은 다음과 같다.[1]
서 및 는 a와 b의 두 위치를 나타내는 n 벡터다. 은 각차이며, 따라서 지구 반지름과 곱하여 원 거리를 달성한다. 이 표현은 극과 ±180° 자오선에서도 작용한다.
벡터 대수학의 사용이 표준 문제를 단순화하는 몇 가지 다른 예가 있다.[1] 다양한 표현에 대한 일반적인 비교는 수평 위치 표현 페이지를 참조하십시오.
참고 항목
참조
- ^ Jump up to: a b c d Gade, Kenneth (2010). "A non-singular horizontal position representation" (PDF). The Journal of Navigation. Cambridge University Press. 63 (3): 395–417. doi:10.1017/S0373463309990415.
- ^ Stuelpnagel, John (1964). "On the Parametrization of the Three-Dimensional Rotation Group". SIAM Review. Society for Industrial and Applied Mathematics. 6 (4): 422–430. doi:10.1137/1006093. JSTOR 2027966.
![{\mathbf n}^{e}=\left[{\begin{matrix}\cos({\mathrm {latitude}})\cos({\mathrm {longitude}})\\\cos({\mathrm {latitude}})\sin({\mathrm {longitude}})\\\sin({\mathrm {latitude}})\\\end{matrix}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b2d5791ce596011391b1f54ca2631cfc501bf2)








 a와 b의 두 위치를 나타내는 n 벡터다.
a와 b의 두 위치를 나타내는 n 벡터다. 


