맥스웰의 악마

Maxwell's demon
맥스웰의 악마적 사고 실험의 개략도

맥스웰의 악마는 열역학 제2법칙에 위배되는 사고 실험이다.이것은 물리학자 제임스 클럭 맥스웰에 의해 [1]1867년에 제안되었다.그의 첫 번째 편지에서 맥스웰은 악마를 "확실한 존재"라고 불렀고 데몬의 이름은 [2]켈빈 경에 의해 처음 사용되었다.

사고 실험에서, 악마는 두 개의 가스실 사이에 있는 질량이 없는 작은 문을 통제한다.개개의 가스 분자(또는 원자)가 문으로 접근하면, 악마는 빠르게 움직이는 분자만이 한 방향으로 통과하고, 느리게 움직이는 분자만이 다른 방향으로 통과하도록 하기 위해 문을 빠르게 여닫습니다.가스의 운동 온도는 구성 분자의 속도에 따라 달라지기 때문에, 악마의 작용으로 인해 한쪽 방은 따뜻해지고 다른 한쪽은 식게 됩니다.이것은 어떠한 작업도 가하지 않고 두 가스의 총 엔트로피를 감소시켜 열역학 제2법칙을 위반할 것이다.

맥스웰의 악마라는 개념은 오늘날까지 계속되고 있는 과학과 이론 물리학의 철학에서 상당한 논쟁을 불러일으켰다.그것은 열역학과 정보 이론 사이의 관계에 대한 연구를 자극했다.대부분의 과학자들은 이론적인 근거로 어떠한 실용적인 장치도 이런 식으로 제2법칙을 위반할 수 없다고 주장한다.비록 모든 것이 사고 실험과 어느 정도 다르고 어떤 것도 제2법칙을 위반하는 것으로 나타나지 않았지만, 다른 연구자들은 맥스웰의 악마의 형태를 실험에 구현했다.

아이디어의 기원과 역사

사고 실험은 맥스웰이 1867년 12월 11일 피터 거스리 타이트에게 쓴 편지에서 처음 나타났다.그것은 맥스웰의 1872년 열역학 책인 [3]열역학에서 대중에게 소개되기 전인 1871년 존 윌리엄 스트럿에게 보낸 편지에서 다시 나타났다.

그의 편지와 책에서 맥스웰은 방들 사이의 문을 여는 요원을 "확실한 존재"라고 묘사했다.윌리엄 톰슨(켈빈 경)은 1874년 네이처 저널에서 맥스웰의 개념을 위해 악마라는 단어를 처음 사용했으며, 그가 악의 있는 [4][5][6]존재가 아닌 배경에서 일하는 초자연적인 존재인 데몬에 대한 그리스 신화 해석을 의도했음을 암시했다.

독창적인 사고 실험

열역학 제2법칙은 (통계적 확률을 통해) 다른 온도의 두 물체가 서로 접촉하고 우주의 나머지 부분으로부터 분리될 때, 두 물체가 거의 [7]같은 온도를 갖는 열역학 평형으로 진화할 것을 보장합니다.두 번째 법칙은 고립된 시스템에서는 엔트로피가 절대 [7]감소하지 않는다는 주장으로도 표현됩니다.

맥스웰은 제2법칙에 대한 이해를 증진시키는 방법으로 사고실험을 구상했다.실험에 대한 그의 설명은 다음과 같다.[7][8]

...만약 우리가 능력이 매우 날카로워져서 그 과정에서 모든 분자를 따라갈 수 있는 존재를 상상한다면, 우리의 특성만큼 본질적으로 유한한 존재는 우리에게 불가능한 것을 할 수 있을 것이다.우리는 균일한 온도에서 공기로 가득 찬 용기 안의 분자가 일정한 속도로 움직이는 것을 보아왔기 때문에 임의로 선택된 수많은 분자의 평균 속도는 거의 균일하다.이러한 혈관이 작은 구멍이 있는 분할에 의해 A와 B의 두 부분으로 나뉘어져 각각의 분자를 볼 수 있는 존재가 이 구멍을 열고 닫고 스위프터 분자만 A에서 B로, 느린 분자만 B로 통과한다고 가정해 봅시다.따라서 그는 열역학 제2법칙에 반하여 작업비용 없이 B의 온도를 올리고 A의 온도를 낮춘다.

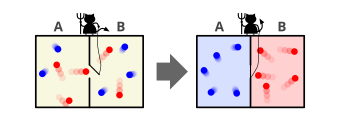
즉, Maxwell은 A와 [7][9]B의 두 부분으로 나뉜 하나의 용기를 상상한다.두 부품 모두 동일한 온도에서 동일한 가스로 채워져 서로 옆에 배치됩니다.양쪽의 분자를 관찰하면서 상상 속의 악마가 두 부분 사이의 트랩도어를 지킨다.평균보다 빠른 A 분자가 트랩도어 쪽으로 날아오면 악마는 문을 열고 A에서 B로 날아갑니다.마찬가지로, 평균보다 느린 B 분자가 트랩도어 쪽으로 날아갈 때, 악마는 B에서 A로 지나가게 할 것이다.B에서 분자의 평균 속도는 증가하지만 A에서는 평균 속도가 느려집니다.평균 분자속도는 온도에 해당하기 때문에 열역학 제2법칙과 달리 A에서는 온도가 낮아지고 B에서는 온도가 높아집니다.열저장고 A와 B 사이에 작동하는 열엔진은 이 온도차이에서 유용한 작업을 추출할 수 있다.

악마는 온도 차이만 내기 위해 분자가 양방향으로 통과할 수 있도록 해야 합니다. A에서 B로 가는 분자의 일방통행은 B 쪽에서 더 높은 온도와 압력을 발생시킵니다.

비판과 발전

몇몇 물리학자들은 [7][9][10]악마를 포함한 전체 시스템에 대해 더 완벽한 분석이 이루어진다면 열역학 제2법칙이 실제로 위반되지 않을 것이라는 계산을 제시했습니다.물리적인 논의의 본질은 어떤 악마가 설명된 방법에 의해 제거될 수 있는 것보다 더 많은 엔트로피를 생성해야 한다는 것을 계산으로 보여주는 것입니다.즉, 분자의 속도를 측정하여 A와 B 사이의 개구부를 선택적으로 통과시키는 것은 온도 차이로 인한 에너지 양보다 더 많은 열역학적 작업이 필요할 것이다.

이 질문에 대한 가장 유명한 답변 중 하나는 1929년 레오 [11]실라르드에 의해 제안되었고, 후에 레옹 브릴루인에 [7][9]의해 제안되었다.실생활의 맥스웰의 악마는 분자속도를 측정할 수 있는 수단을 가져야 하며, 정보를 획득하는 행위는 에너지 소비를 필요로 할 것이라고 Szilarrd는 지적했다.악마와 가스는 상호작용을 하기 때문에 가스와 악마를 합친 총 엔트로피를 고려해야 합니다.악마의 에너지 소비는 악마의 엔트로피를 증가시키고, 이는 가스의 엔트로피를 감소시키는 것보다 클 것이다.

1960년, 롤프 란다우어는 이 [7][9][12]주장에 대해 예외를 제기했다.그는 일부 측정 과정이 열역학적으로 가역적이면 열역학적 엔트로피를 증가시킬 필요가 없다는 것을 깨달았다.그는 이러한 "역할 수 있는" 측정이 제2법칙에 위반되는 분자들을 분류하는데 사용될 수 있다고 제안했다.그러나 열역학적 엔트로피와 정보 엔트로피 간의 연관성 때문에 기록된 측정치가 지워져서는 안 된다는 의미도 있었습니다.다른 말로 하자면, 분자를 통과시킬지 결정하기 위해, 악마는 분자의 상태에 대한 정보를 얻고 그것을 버리거나 저장해야 한다.그것을 폐기하면 엔트로피가 즉시 증가하지만 악마는 그것을 무한정 저장할 수 없다.1982년 Charles Bennett은 아무리 준비가 잘 되어 있어도 결국 정보 저장 공간이 부족해지고 이전에 수집한 정보를 [9][13]삭제하기 시작해야 한다는 것을 보여주었습니다.정보를 지우는 것은 시스템의 엔트로피를 증가시키는 열역학적으로 돌이킬 수 없는 과정이다.베넷은 1929년 실라드의 논문과 같은 결론에 도달했지만 맥스웰의 악마는 엔트로피가 생성되기 때문에 제2의 법칙을 위반할 수 없다는 결론에 도달했다.란다우어의 원리와 관련하여, 정보 삭제로 인한 최소 에너지는 2012년에 에릭 루츠 등에 의해 실험적으로 측정되었다.또한, Lutz 등은 Landauer의 한계에 접근하기 위해서는 시스템이 점근적으로 0 [14]처리 속도에 접근해야 한다고 확인했다.

존 얼먼과 존 D. 노튼은 맥스웰의 악마에 대한 실라드와 란다우어의 설명은 열역학 제2법칙이 악마에 의해 위반될 수 없다는 가정으로부터 시작되며, 정보를 지울 때 에너지를 소비해야 한다는 [15][16]등의 가정으로부터 악마의 추가적인 특성을 도출한다고 주장했다.그러므로 악마적 논쟁으로부터 제2의 법칙을 방어하기 위해 이러한 파생된 특성들을 호출하는 것은 순환적일 것이다.베넷은 나중에 에르만과 노튼의 주장의 타당성을 인정하면서, 란다우어의 원리는 실제 시스템이 [17]열역학 제2법칙을 위반하지 않는 메커니즘을 설명한다고 주장했다.

최근 진행 상황

Landauer와 Bennett에 의한 주장은 열역학 제2법칙과 실라드 엔진(엔진과 악마의 복합 시스템)의 전체 시스템의 전체 순환 과정 사이의 일관성에 대한 답변에 불과하지만, 작은 변동 시스템에 대한 비균형 열역학에 기초한 최근의 접근은 더 깊은 곳에서 제공되었습니다.각 서브시스템에서 각 정보 프로세스를 확인할 수 있습니다.이 관점에서 측정 프로세스는 엔진과 데몬의 상관관계(상호정보)가 증가하는 프로세스로, 피드백 프로세스는 상관관계가 감소하는 프로세스로 간주된다.상관관계가 변화하면 열역학 제2법칙으로서의 열역학 관계와 각 서브시스템에 대한 변동정리를 수정해야 하며, 외부제어의 경우[18] 부등식과 같은 제2법칙과 상호정보에 의한 일반화 변동정리가[19] 충족된다.이러한 관계는 상관관계를 증가시키기 위해 추가적인 열역학적 비용이 필요하다는 것을 시사하며(측정 사례), 반대로 상관관계를 소비하기까지의 제2법칙(피드백 사례)을 명백히 위반할 수 있다.생물학적 정보처리를 포함한 보다 일반적인 정보처리는 상호정보와의 불평등과[20][21] 평등이 모두 존재한다.

적용들

맥스웰의 악마의 실제 버전은 발생하지만, 그러한 모든 "실제 악마" 또는 분자 악마들은 [22]다른 곳에서 엔트로피의 증가에 의해 적절히 균형을 잡습니다.분자 크기의 메커니즘은 더 이상 생물학에서만 찾아볼 수 있는 것이 아니라 나노 기술의 신흥 분야의 주제이기도 합니다.입자 물리학자들이 사용하는 단일 원자 함정은 실험자들이 맥스웰의 악마와 유사한 방식으로 개별 양자 상태를 제어할 수 있게 해준다.

만약 가상의 거울 물질이 존재한다면, Zurab Silagadze는 악마가 예견될 수 있다고 제안합니다. 악마는 두 번째 종류의 영구 이동체처럼 작용할 수 있습니다. 즉, 오직 한 개의 저장고에서만 열에너지를 추출하고, 작업을 하고, 나머지 평범한 세계로부터 격리되기 위해 사용됩니다.하지만 제2법칙은 위반되지 않는다.왜냐하면 악마는 거울 [23]광자를 방출함으로써 세상의 숨겨진(거울) 분야에서 엔트로피 비용을 지불하기 때문이다.

실험 작업

2007년 2월호 네이처지에서 에든버러 대학의 데이비드 레이 교수는 리처드 파인만이 대중화한 브라운식 래칫을 기반으로 한 나노 디바이스의 개발을 발표했다.리의 장치는 화학 시스템을 평형에서 벗어나게 할 수 있지만, 외부 소스(이 경우 빛)에 의해 구동되어야 하므로 열역학을 [24]위반하지 않습니다.

이전에 노벨상 수상자인 프레이저 스토다트를 포함한 연구원들은 A와 B를 연결하는 축 위에 놓일 수 있는 로탁산이라고 불리는 고리 모양의 분자를 만들었다.어느 한 곳에서 온 입자가 링에 부딪혀 링을 끝에서 끝까지 움직입니다.이러한 디바이스의 대규모 컬렉션이 시스템에 배치되어 있는 경우,[25] 어느 시점에서라도 디바이스의 절반은 사이트 A에 링을, 절반은 B에 링을 가지고 있었습니다.

리는 장치에 빛이 비칠 경우 차축의 중심이 두꺼워져 링의 움직임이 제한되도록 차축을 약간 변경했습니다.단, A에 있는 경우 링이 움직이지 않도록 할 뿐입니다.따라서 시간이 지남에 따라 링은 B에서A로 범핑되어 거기에 고착되어 시스템에 불균형이 생깁니다.실험에서 리는 몇 분 안에 50:[26]50의 평형에서 70:30의 불균형으로 "수십억 개의 장치"를 한 냄비에 담을 수 있었다.

2009년 마크 G. 라이젠은 맥스웰이 가스 내의 개별 원자를 그들의 [7][27][28]에너지에 따라 다른 용기에 분류하는 과정을 실현하는 레이저 원자 냉각 기술을 개발했다.새로운 개념은 원자나 분자가 한 방향으로 움직일 수 있게 하지만 되돌아가지 못하게 하는 단방향 벽이다.단방향 벽의 작동은 특정 파장에서 광자를 흡수하는 돌이킬 수 없는 원자 및 분자 과정에 의존하며, 그 후 다른 내부 상태로의 자발적 방출이 뒤따른다.돌이킬 수 없는 과정은 자기장 및/또는 빛에 의해 생성된 보존력과 결합됩니다.라이젠과 공동 연구자들은 원자의 집합의 엔트로피를 줄이기 위해 단방향 벽을 사용할 것을 제안했다.이와 병행하여, 곤살로 무가와 안드레아스 루샤프트는 독립적으로 유사한 개념을 개발했다.그들의 "원자 다이오드"는 냉각을 위한 것이 아니라 원자의 흐름을 조절하기 위해 제안되었다.라이젠 그룹은 2008년 일련의 실험에서 단방향 벽으로 원자의 상당한 냉각을 증명했다.그 후, 원자에 대한 편도 벽의 작동은 2008년 후반에 다니엘 스텍과 협력자들에 의해 입증되었다.이들의 실험은 2005년 단방향 벽의 스킴에 기초하고 있으며 냉각에는 사용되지 않았다.라이젠 그룹에 의해 실현된 냉각 방법은 원자를 거의 정지 상태로 만들기 위해 평균 한 개의 광자만 필요하기 때문에 "단일 광자 냉각"이라고 불렸다.이는 광자의 운동량을 사용하고 2레벨 사이클 전환이 필요한 다른 레이저 냉각 기법과 대조적이다.

2006년, 라이젠, 무가, 러쉬하우트는 이론 논문에서 각 원자가 단방향 벽을 통과할 때 하나의 광자를 산란하고, 전환점과 그 입자의 에너지에 대한 정보가 제공된다는 것을 보여주었다.지향성 레이저에서 랜덤 방향으로 산란된 방사장의 엔트로피 증가는 원자가 단방향 벽에 갇힐 때의 엔트로피 감소에 의해 정확히 균형을 이룬다.

이 기술은 높은 에너지 원자와 낮은 에너지 원자를 다른 용기에 분류해 온도차를 만드는 맥스웰의 과정을 실현하기 때문에 '맥스웰의 악마'로 널리 알려져 있다.하지만, 과학자들은 이것이 열역학 [7][29]제2법칙에 위배되지 않는다는 점에서 진정한 맥스웰의 악마가 아니라고 지적했습니다; 그것은 엔트로피의 순[7][29] 감소를 초래하지 않고 유용한 에너지를 생산하는데 사용될 수 없습니다.이는 프로세스에서 발생하는 온도 차이로 인해 발생할 수 있는 것보다 더 많은 에너지가 레이저 빔에서 필요하기 때문입니다.원자는 레이저광에서 낮은 엔트로피 광자를 흡수해 무작위로 방출해 환경의 [7][29]엔트로피를 높인다.

2014년 Pekola 등은 Szilarrd [30][31]엔진의 실험적인 실현을 시연했다.불과 1년 후, 이전의 이론적인 [32]제안을 바탕으로, 같은 그룹은 시스템에서 미세한 정보를 추출하고 피드백을 적용하여 엔트로피를 감소시키는 자율적인 맥스웰의 악마의 첫 번째 실험적인 실현을 제시했다.데몬은 동일한 전자 회로에 통합된 두 개의 용량 결합 단일 전자 소자를 기반으로 합니다.데몬의 작동은 시스템의 온도 강하로 직접 관찰되며, [33]데몬의 온도 상승은 상호 정보 생성에 따른 열역학 비용에서 발생합니다.2016년 Pekola 등은 결합된 단일 전자 회로에서 자율 악마의 원리 증명을 시연하여 정보를 [34]연료로 회로 내의 중요 소자를 냉각하는 방법을 보여주었다.페콜라 등또한 초전도 회로로 만들어진 단순한 큐비트 회로가 양자 질라드의 [35]엔진을 연구하기 위한 기초를 제공할 수 있다고 제안했다.

은유로서

일반적으로 사용자에게 응답하기 위해 서버에서 실행되는 프로세스인 컴퓨팅의 데몬은 Maxwell의 [36]악마의 이름을 따서 명명되었습니다.

역사학자 헨리 브룩스 애덤스는 그의 원고 "역사에 적용되는 위상 규칙"에서 맥스웰의 악마를 역사적 은유로 사용하려고 시도했지만, 그는 원래의 [37]원리를 오해하고 잘못 적용했다.애덤스는 역사를 "균형"을 향해 나아가는 과정으로 해석했지만, 그는 군국주의 국가(그는 독일이 이 계급에서 우월하다고 느꼈다)가 맥스웰의 역사 악마인 이 과정을 되돌리는 경향이 있다고 보았다.애덤스는 그의 연구 동료들로부터 그의 공식화에 대한 비판에 답하기 위해 많은 시도를 했지만, 그 작업은 1918년 애덤스가 사망했을 때 미완성으로 남아있었다.그것은 [38]사후에 출판되었을 뿐이다.

「 」를 참조해 주세요.

메모들

  1. ^ Cargill Gilston Knott (1911). "Quote from undated letter from Maxwell to Tait". Life and Scientific Work of Peter Guthrie Tait. Cambridge University Press. pp. 213–215.
  2. ^ [1]
  3. ^ Leff & Rex (2002), 페이지 370.
  4. ^ William Thomson (1874). "Kinetic theory of the dissipation of energy". Nature. 9 (232): 441–444. Bibcode:1874Natur...9..441T. doi:10.1038/009441c0.
  5. ^ "The sorting demon of Maxwell". Nature. 20 (501): 126. 1879. Bibcode:1879Natur..20Q.126.. doi:10.1038/020126a0.
  6. ^ Alan S. Weber (2000). Nineteenth Century Science: a Selection of Original Texts. Broadview Press. p. 300.
  7. ^ a b c d e f g h i j k Bennett, Charles H. (November 1987). "Demons, Engines, and the Second Law" (PDF). Scientific American. 257 (5): 108–116. Bibcode:1987SciAm.257e.108B. doi:10.1038/scientificamerican1187-108. Retrieved November 13, 2014.
  8. ^ 맥스웰(1871)은 4페이지 레프앤렉스에 전재됐다.
  9. ^ a b c d e Sagawa, Takahiro (2012). Thermodynamics of Information Processing in Small Systems. Springer Science and Business Media. pp. 9–14. ISBN 978-4431541677.
  10. ^ Bennett, Charles H.; Schumacher, Benjamin (August 2011). "Maxwell's demons appear in the lab" (PDF). Nikkei Science: 3–6. Retrieved November 13, 2014.
  11. ^ 실라르드, 레오(1929년)."Über Entropieverminderungeinemthermodynamischen 시스템bei Eingriffen에 다이 intelligenter 본질(엔트로피의 열역학적 시스템에 지적 생명체의 중재로 감소 탭에서".Zeitschrift für Physik.53(11–12):840–856.Bibcode:1929ZPhy...53..840S. doi:10.1007/bf01341281.S2CID 122038206. 베넷 1987년에 인용한.NASA 문서 TT F-16723 영문 번역본 1976년 발행
  12. ^ Landauer, R. (1961). "Irreversibility and heat generation in the computing process" (PDF). IBM Journal of Research and Development. 5 (3): 183–191. doi:10.1147/rd.53.0183. Retrieved November 13, 2014. 제44권, 제1호, 2000년 1월, 261페이지에 전재되었다.
  13. ^ Bennett, C. H. (1982). "The thermodynamics of computation—a review" (PDF). International Journal of Theoretical Physics (Submitted manuscript). 21 (12): 905–940. Bibcode:1982IJTP...21..905B. CiteSeerX 10.1.1.655.5610. doi:10.1007/BF02084158. S2CID 17471991. Archived from the original (PDF) on 2014-10-14. Retrieved 2017-12-10.
  14. ^ Ball, Philip (2012). "The unavoidable cost of computation revealed". Nature. doi:10.1038/nature.2012.10186. S2CID 2092541.
  15. ^ John Earman & John D. Norton (1998). "Exorcist XIV: The Wrath of Maxwell's Demon. Part I. From Maxwell to Szilard" (PDF). Studies in History and Philosophy of Modern Physics. 29 (4): 435. Bibcode:1998SHPMP..29..435E. doi:10.1016/s1355-2198(98)00023-9.
  16. ^ John Earman & John D. Norton (1999). "Exorcist XIV: The Wrath of Maxwell's Demon. Part II. From Szilard to Landauer and Beyond" (PDF). Studies in History and Philosophy of Modern Physics. 30 (1): 1. Bibcode:1999SHPMP..30....1E. doi:10.1016/s1355-2198(98)00026-4.
  17. ^ Charles H. Bennett (2002–2003). "Notes on Landauer's principle, reversible computation, and Maxwell's demon". Studies in History and Philosophy of Modern Physics. 34 (3): 501–510. arXiv:physics/0210005. Bibcode:2003SHPMP..34..501B. doi:10.1016/S1355-2198(03)00039-X. S2CID 9648186.
  18. ^ Hugo Touchette & Seth Lloyd (2000). "Information-Theoretic Limits of Control". Physical Review Letters. 84 (6): 1156–1159. arXiv:chao-dyn/9905039. Bibcode:2000PhRvL..84.1156T. doi:10.1103/PhysRevLett.84.1156. PMID 11017467. S2CID 25507688.
  19. ^ Takahiro Sagawa & Masahito Ueda (2010). "Generalized Jarzynski Equality under Nonequilibrium Feedback Control". Physical Review Letters. 104 (9): 090602. arXiv:0907.4914. Bibcode:2010PhRvL.104i0602S. doi:10.1103/PhysRevLett.104.090602. PMID 20366975. S2CID 1549122.
  20. ^ Armen E Allahverdyan, Dominik Janzing and Guenter Mahler (2009). "Thermodynamic efficiency of information and heat flow". Journal of Statistical Mechanics: Theory and Experiment. 2009 (9): P09011. arXiv:0907.3320. Bibcode:2009JSMTE..09..011A. doi:10.1088/1742-5468/2009/09/P09011. S2CID 118440998.
  21. ^ Naoto Shiraishi & Takahiro Sagawa (2015). "Fluctuation theorem for partially masked nonequilibrium dynamics". Physical Review E. 91 (1): 012130. arXiv:1403.4018. Bibcode:2015PhRvE..91a2130S. doi:10.1103/PhysRevE.91.012130. PMID 25679593. S2CID 1805888.
  22. ^ R., Loewenstein, Werner (2013-01-29). Physics in mind : a quantum view of the brain. New York. ISBN 9780465029846. OCLC 778420640.
  23. ^ Silagadze, Z. K (2007). "Maxwell's demon through the looking glass". Acta Physica Polonica B. 38 (1): 101–126. arXiv:physics/0608114. Bibcode:2007AcPPB..38..101S.
  24. ^ Serreli, V; Lee, CF; Kay, ER; Leigh, DA (February 2007). "A molecular information ratchet". Nature. 445 (7127): 523–527. Bibcode:2007Natur.445..523S. doi:10.1038/nature05452. PMID 17268466. S2CID 4314051.
  25. ^ Bissell, Richard A; Córdova, Emilio; Kaifer, Angel E.; Stoddart, J. Fraser (12 May 1994). "A chemically and electrochemically switchable molecular shuttle". Nature. 369 (6476): 133–137. Bibcode:1994Natur.369..133B. doi:10.1038/369133a0. S2CID 44926804.
  26. ^ Katharine Sanderson (31 January 2007). "A demon of a device". Nature. doi:10.1038/news070129-10. S2CID 121130699.
  27. ^ Raizen, Mark G. (June 12, 2009). "Comprehensive Control of Atomic Motion". Science. 324 (5933): 1403–1406. Bibcode:2009Sci...324.1403R. doi:10.1126/science.1171506. PMID 19520950. S2CID 10235622.
  28. ^ Raizen, Mark G. (March 2011). "Demons, Entropy, and the Quest for Absolute Zero". Scientific American. 304 (3): 54–59. Bibcode:2011SciAm.304c..54R. doi:10.1038/scientificamerican0311-54. PMID 21438491. Retrieved November 14, 2014.
  29. ^ a b c Orzel, Chad (January 25, 2010). "Single-Photon Cooling: Making Maxwell's Demon". Uncertain Principles. ScienceBlogs website. Retrieved November 14, 2014.
  30. ^ Koski, J.V.; Maisi, V.F.; Sagava, T.; Pekola, J.P. (14 Jul 2014). "Experimental Observation of the Role of Mutual Information in the Nonequilibrium Dynamics of a Maxwell Demon". Physical Review Letters. 113 (3): 030601. arXiv:1405.1272. Bibcode:2014PhRvL.113c0601K. doi:10.1103/PhysRevLett.113.030601. PMID 25083623.
  31. ^ Koski, J.V.; Maisi, V.F.; Pekola, J.P.; Averin, D.V. (23 Sep 2014). "Experimental realization of a Szilard engine with a single electron". Proceedings of the National Academy of Sciences of the United States of America. 111 (38): 13786–9. arXiv:1402.5907. Bibcode:2014PNAS..11113786K. doi:10.1073/pnas.1406966111. PMC 4183300. PMID 25201966.
  32. ^ Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. (24 Jan 2013). "Thermodynamics of a Physical Model Implementing a Maxwell Demon". Physical Review Letters (Submitted manuscript). 110 (4): 040601. arXiv:1210.5661. Bibcode:2013PhRvL.110d0601S. doi:10.1103/PhysRevLett.110.040601. PMID 25166147. S2CID 5782312.
  33. ^ Koski, J.V.; Kutvonen, A.; Khaymovich, I.M.; Ala-Nissila, T.; Pekola, J.P. (2015). "On-Chip Maxwell's Demon as an Information-Powered Refrigerator". Physical Review Letters. 115 (26): 260602. arXiv:1507.00530. Bibcode:2015PhRvL.115z0602K. doi:10.1103/PhysRevLett.115.260602. PMID 26764980. S2CID 3393380.
  34. ^ Koski, J.V.; Pekola, J.P. (16 Dec 2016). "Maxwell's demons realized in electronic circuits". Comptes Rendus Physique. 17 (10): 1130–1138. Bibcode:2016CRPhy..17.1130K. doi:10.1016/j.crhy.2016.08.011.
  35. ^ Pekola, J.P.; Golubev, D.S.; Averin, D.V. (5 Jan 2016). "Maxwell's demon based on a single qubit". Physical Review B. 93 (2): 024501. arXiv:1508.03803. Bibcode:2016PhRvB..93b4501P. doi:10.1103/PhysRevB.93.024501. S2CID 55523206.
  36. ^ Fernando J. Corbató (2002-01-23). "Take Our Word for It". Retrieved 2006-08-20.
  37. ^ Cater(1947), 페이지 640–647; Leff & Rex(1990), 페이지 37–51에 전재된 Daub(1970)도 참조한다.
  38. ^ 애덤스(1919), 페이지 267.

레퍼런스

  • Cater, H. D., ed. (1947). Henry Adams and his Friends. Boston.
  • Daub, E. E. (1967). "Atomism and Thermodynamics". Isis. 58 (3): 293–303. doi:10.1086/350264. S2CID 143459461.
  • Leff, Harvey S. & Andrew F. Rex, ed. (1990). Maxwell's Demon: Entropy, Information, Computing. Bristol: Adam-Hilger. ISBN 978-0-7503-0057-5.
  • Leff, Harvey S. & Andrew F. Rex, ed. (2002). Maxwell's Demon 2: Entropy, Classical and Quantum Information, Computing. CRC Press. ISBN 978-0-7503-0759-8.
  • Adams, H. (1919). The Degradation of the Democratic Dogma. New York: Kessinger. ISBN 978-1-4179-1598-9.

외부 링크

위키 인용문에는 맥스웰의 악마와 관련된 인용문이 있다.