교차로(유클리드 기하학)

이 문서는 교차로(수학)에 요약되어 있어야 하며, 여기서부터 여기까지의 링크에서 다음 링크를 사용하여 제공되어야 합니다.{{Main}} 템플릿입니다. Wikipedia 안내 참조:요약 스타일.(2020년 11월)

기하학에서 교차로는 두 개 이상의 객체(예: 선, 원곡선, 평면 및 표면)에 공통되는 점, 선 또는 원곡선입니다.유클리드 기하학에서 가장 간단한 경우는 두 개의 뚜렷한 선들의 교차점인데, 선들이 평행하다면 그것은 한 점이거나 존재하지 않는다.

평면 교차점 결정(고차원 공간에 내장된 선형 기하학적 객체)은 선형 대수의 단순한 작업, 즉 선형 방정식 시스템의 해법이다.일반적으로 교차점의 결정은 비선형 방정식으로 이어지며, 이는 예를 들어 뉴턴 반복을 사용하여 수치적으로 풀 수 있습니다.선과 원뿔 단면(원, 타원, 포물선 등) 또는 4차원(구면, 원통, 쌍곡선 등)의 교차 문제는 쉽게 풀 수 있는 2차 방정식으로 이어진다.사분원 사이의 교차는 대수적으로 풀 수 있는 사분원 방정식으로 이어진다.

비행기 안에서

2개의 선.

평행하지 않은 두 선의 교차점 결정

${\displaystyle a_{1}x+b_{1}y=c_{1},\a_{2}x+b_{2}y=c_{2}}$

Cramer 규칙에서 또는 변수를 대입하여 교차점의${\displaystyle }$좌표(${\displaystyle x_{}}$s , ${\displaystyle {}_{}{s}_{}}$) {$displaystyle (x_{s$ , $y_{s}$ )$$를 얻을 수 있습니다.

${\displaystyle x_{s}=secfrac {c_{1}b_{2}b_{1}}{a_{2}b_{2},\sec y_{s}=secfrac {a_{1}c_{2}-a_{2}_{1}{1}{1},\s}_s}=secfrac {a_{a}_{1}_{1}\ }$

(${\displaystyle {a\mathrm{}}_{}}$ 1 ${\displaystyle {b\mathrm{}}_{}}$2 - ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ $=$ {\$displaystyle a_{1}b_{2$}-$a_{2}b_${1}=$0}$인 $경우{\displaystyle {}_{}}$ 선은 평행하며 이러한 공식은 0으로 나누기 때문에 사용할 수 없습니다.)

2개의 선분

이 섹션을 선분교차라는 제목의 다른 기사로 분할할 것을 제안했다.(논의) (2020년 11월)

2개의 비병렬 선분$({\displaystyle {}_{}{}_{}}$1, y${\displaystyle {}_{}{1\mathrm{}}_{}),}$ (${\displaystyle {x\mathrm{}}_{}}$2, ${\displaystyle {y\mathrm{}}_{}}$ $2 ),$ ($x_$${1}),$ (${\displaystyle {}_{}}$${2}),$ $({\displaystyle {x\mathrm{}}_{}}$ 3, ${\displaystyle {y\mathrm{}}_{}}$$$3${\displaystyle ),}$(${\displaystyle {x\mathrm{}}_{}}$ 4 $),$ (x 4 )($x_{3}, y_{4}),$ ($x_{4$})에는$$ 반드시 해당되지 않습니다.${\displaystyle {}_{}}$대응하는$$라인의 {\$displaystyle(x_{0,y_{0})}$은(는) 라인 세그먼트에 포함할 필요가 없습니다${\displaystyle .}$상황을 확인하기 위해 라인의 파라메트릭 표현을 사용합니다.

$({displaystyle(x),y(s)=(x_{1}+s(x_{2}-x_{1}),y_{1}+s(y_{2}-y_{1}),}$

$({displaystyle(x(t),y(t)=(x_{3}+t(x_{4}-x_{3}),y_{3}+t(y_{4}-y_{3})).}$

회선 세그먼트는 대응하는 ${\displaystyle {파라미터}_{}}$가 0${\displaystyle ,}$ ${\displaystyle {t0\mathrm{}}_{}}$, t0$,$ $t_{0}$인 경우 대응하는 회선의 공통점$x0$ $)$에서만 교차합니다$.{0$} {\displaystyle $,$ $t_{0$$} {\$$displaystyle$$$0$\leq s_0}$ {$0$$$1 .${\displaystyle {t\mathrm{}}_{}}$ 0$(\$은 선형 시스템의 솔루션입니다.

$\displaystyle s(x_{2}-x_{1})-t(x_{4}-x_{3}=x_{3}-x_{1}$

$\displaystyle s(y_{2}-y_{1})-t(y_{4}-y_{3}=y_{3}-y_{1}\ .}$

Cramer의 법칙을 사용하여 및 t에 대해 해결할 수 있습니다(위 참조).$조건{\displaystyle \mathrm{}}$ 0${\displaystyle {\mu s\mathrm{}}_{}}$0, ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}\mathrm{\mu }}$1 {\$displaystyle 0\leq s_{0$$$},$t_$${$0}\$leq$ 1$$$}$이 충족되면 대응하는 파라미터 ${\displaystyle {표현}_{}}$에 s$$0(\$displaystyle$ $s_{0$}) ${\displaystyle {또는\mathrm{}}_{}}$t 0(\$displaystyle$$$t_${0$을 $삽입$하여 교차점$x$0, $)$을 가져옵니다.

예:회선 세그먼트$({\displaystyle 1,1),}$ (${\displaystyle 3}$,${\displaystyle }$2$)$ {$displaystyle(1$,$1),$ (${\displaystyle 3}$$, 2)}$ 및${\displaystyle }$(${\displaystyle 1}$, 4${\displaystyle }),{\displaystyle }$(${\displaystyle 2,}$-${\displaystyle 1}$)$${$displaystyle(1, 4),$ (2$,$1)}의$$$$ 경우 선형 시스템을 가져옵니다.

${\displaystyle 2s-t=0}$

${\displaystyle s+5t=3}$

${\displaystyle {및\mathrm{}}_{}}$ s 0 ${\displaystyle {}_{}}$ ${\displaystyle 3\frac{\mathrm{}}{}}$ ${\displaystyle \frac{11}{}}$ ${\displaystyle ,}$ ${\displaystyle {t\mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle 6\frac{\mathrm{}}{}}$ ${\displaystyle \frac{11}{}}$ ${$ { $displaystyle$ s$_${ $0$} =$t_${ 0 } =$tftfrac$ { $6$}} $。$즉$,{\displaystyle }$ 선은 (${\displaystyle \frac{17}{}}$, ${\displaystyle \frac{14}{}}$ $)$ 지점에서 교차합니다.{ $displaystyle${ \$tfrac${ $17}$ { $11}$} $。$

비고: 점의 쌍으로 결정되는 선이 아닌 선을 고려하여 각 $조건{\displaystyle \mathrm{}}$ 0${\displaystyle {}_{}}$ s${\displaystyle {}_{}{0\mathrm{}}_{}}$ 、 ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}1}$1 { $displaystyle$0 \ $leq$ s$_$ {$0$ } , $t$_ { $0$} \$leq$1 을 드롭하고$$, 이 방법으로 선의 교차점을 산출할 수 있습니다(위 참조).

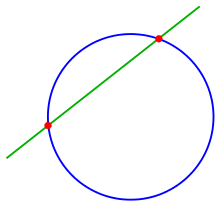
선과 원

의 교차점에 대하여

• $라인{\displaystyle }$ ${\displaystyle a}$ x${\displaystyle }$+ ${\displaystyle b}$ y ${\displaystyle =}$ { $display style$ax + $by$=$c$} 및$$ 원 $x{\displaystyle {}^{}{2\mathrm{}}^{}}$ + ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ { \ $display style$ x$^$ {2} + y ^ { $2$ }$}=r^{2}}$

하나는 x 또는 y에 대한 선 방정식을 풀고 그것을 원의 방정식으로 대체하고 (2차 방정식의 공식을 사용하여$){\displaystyle }$ (${\displaystyle {x\mathrm{}}_{}{}_{}}$, ${\displaystyle {y\mathrm{}}_{}}$1 ${\displaystyle ),}$ (${\displaystyle {}_{}{}_{}}$2, ${\displaystyle {y\mathrm{}}_{}}$2)$${$style$ $(x_{1}),$ ($x_{2$}) 를 $구한다.$

${\displaystyle x_{1/2}=subscfrac {ac\pm bsubrt {r^{2}(a^{2}+b^{2})-c^{2}}}:{a^{2}+b^{2}}}}\ ,}$

${\displaystyle y_{1/2}=bc\mp a440rt {r^{2}(a^{2}+b^{2})-c^{2}}}:{a^{2}+b^{2}}}}\ ,}$

${\displaystyle {r\mathrm{}}^{}}$ 2${\displaystyle {}^{}{a\mathrm{}}^{}}$2 + ${\displaystyle {}^{}{2\mathrm{}}^{}}$) ${\displaystyle -}$ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}0}$0$$. { $displaystyle$ r$^{2}(a^{2}+b^{2})$ - $c^{2}\geq$ 0$\$ .} 이$$ 조건이 엄격한 부등식으로 유지되면 두 개의 교차점이 있습니다. 이 경우 선을 원의 보조선이라고 하며, 이 선을 현의 교차점이라고 합니다.

${\displaystyle {r\mathrm{}}^{}}$ 2${\displaystyle {}^{}{a\mathrm{}}^{}}$2 + ${\displaystyle {}^{}{2\mathrm{}}^{}}$)${\displaystyle }$- ${\displaystyle {c\mathrm{}}^{}}$ 2 $=$ $({displaystyle$ r$^{2}(a^{2}+b^{2})-c^{2$}=$0)$이 $유지$되면 교점은 1개뿐이고 선은 원에 접하는 것입니다.약한 부등식이 유지되지 않으면 선이 원을 교차하지 않습니다.

원의 중간점이 원점이 아닌 경우 ^[1]를 참조하십시오.선과 포물선 또는 쌍곡선의 교점은 유사하게 처리될 수 있습니다.

두 개의 원

두 원의 교차점 결정

• ${{displaystyle (x-x_{1})^{2}+(y-y_{1})^{2}=r_{1}^{2},\time (x-x_{2})^{2}+(y-y_{2})=r_{2}^2}}$

선과 원이 교차하는 이전 사례로 축소할 수 있습니다.주어진 두 방정식을 빼면 선 방정식을 얻을 수 있습니다.

${{displaystyle 2(x_{2}-x_{1})x+2(y_{1})y=r_{1}^{2}-y_{1}^{2}-r_{2}+x_{2}}^{2}+y_{2}^{2}.}$

이 특별한 선은 두 원의 근선이다.

특수 ${\displaystyle 케이스{}_{}}$ ${\displaystyle {x\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {y\mathrm{}}_{}}$ 2 ${\displaystyle {}_{}}$ { $displaystyle \;x_{1$} =$y_{$1} $= y_${$$$2$}=
이 경우 원점은 첫 번째 원의 중심이고 두 번째 중심은 x축(s. 다이어그램)에 있습니다.라디칼 라인의 방정식은 2 ${\displaystyle {}_{}}$ 2 ${\displaystyle =}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}{2\mathrm{}}_{}^{}}$ - ${\displaystyle {\mathrm{}}_{}^{}}$ + ${\displaystyle {x\mathrm{}}_{}^{}{}_{}^{}}{\displaystyle {\mathrm{}}_{}^{}}$ {\$display \; 2x_{2}x=r_{1}^{2}-r_{2}^{2}+x_{2$}로 단순화됩니다.$}^{$2$$}\;} 교점은 (${\displaystyle {x\mathrm{}}_{}{}_{},}$ ±${\displaystyle {}_{}{y\mathrm{}}_{}}$0 ), ${displaystyle (x_{0$},\$pm y_{$0})로${\displaystyle }$다음과 같이 쓸 수 있습니다.

${\displaystyle x_{0}=black {r_{1}^{2}-r_{2}^2}+x_{2}^{2}}{2x_{2}},\syslog y_{0}=syslogrt {r_{1}^{2}-x_{0}^2}}\ . }$

1 < {{$displaystyle r_{1}^{2}$ <$x_{0}^2$}인 경우, 원에는 공통점이 없습니다.
${\displaystyle {r\mathrm{}}_{}^{}}$ 1 ${\displaystyle {\mathrm{}}_{}^{}}$ $=$ ${\displaystyle {x\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$2 {{$displaystyle r_{1}^{2$}=$x_{0}^2}$인 $경우{\displaystyle {}_{}^{}}$ 원은 공통점을 가지며, 라디칼 선은 공통 접선입니다.

위에서 기술한 모든 일반 케이스는 시프트 및 회전에 의해 특수 케이스로 변환될 수 있습니다.

두 개의 원반(두 개의 원의 내부)의 교차점은 렌즈라고 불리는 형태를 형성합니다.

원뿔형 섹션 2개

타원/하이퍼볼라/포물선의 다른 원뿔 단면과의 교차 문제는 하나의 좌표를 제거함으로써 쉽게 풀 수 있는 2차 방정식의 시스템으로 이어진다.용액을 얻기 위해 원뿔 단면의 특수 특성을 사용할 수 있다.일반적으로 교차점은 뉴턴 반복으로 방정식을 풀어서 결정할 수 있다.a) 두 원뿔이 (방정식에 의해) 암묵적으로 (2차원 뉴턴 반복 b) 암묵적으로 주어지고 다른 원뿔은 1차원 뉴턴 반복이 필요하다.다음 섹션을 참조하십시오.

두 개의 부드러운 곡선

연속적으로 미분할 수 있는(즉, 급커브가 $)$ R $2$의 2개의 곡선$({displaystyle \mathbb${R$}^{2}})$은 평면의 공통점을 가지며 이 지점에서 다음 점이 있는 경우 교차점을 가진다.

a: 다른 접선(횡단 교차로) 또는

b: 공통의 접선이며 서로 교차하고 있습니다(교차 교차로, 그림 참조).

두 곡선이 공통으로 점 S와 접선을 가지지만 서로 교차하지 않으면 점 S에 닿을 뿐입니다.

접촉 교차로는 거의 나타나지 않고 다루기 어렵기 때문에 다음 고려사항은 이 경우를 생략합니다.아래의 어떤 경우에도 필요한 모든 차동 조건이 전제됩니다.교차점의 결정은 항상 뉴턴 반복으로 풀 수 있는 하나 또는 두 개의 비선형 방정식으로 이어집니다.표시되는 케이스의 리스트는 다음과 같습니다.

• ${\displaystyle \text{y}}$ = f 1 ( x${\displaystyle }$) , ${\displaystyle {}_{}}$ ${\displaystyle =}$ ${\displaystyle {f\mathrm{}}_{}{2\mathrm{}}_{}}$ ($x$ ) { ${\displaystyle {}_{}}$y$= f_{1$}($x),$ \ y$$=$f_{2}($ 두 곡선이 모두 명시적으로 주어진 경우 등식을 구하면 방정식이 $생성$됩니다.

${\displaystyle f_{1}(x)=f_{2}(x)\ .}$

• 두 곡선이 파라미터로 지정되어 있는 경우: ${\displaystyle {}_{}}$1 : ( ${\displaystyle {x\mathrm{}}_{}}$1 (${\displaystyle t}$) , ${\displaystyle {y\mathrm{}}_{}{}_{}1}$ (${\displaystyle }$t ) , ${\displaystyle \text{C}{}_{}}$2 : (${\displaystyle {}_{}x}$ 2${\displaystyle }$) , ${\displaystyle {y\mathrm{}}_{}2}$ ( s${\displaystyle }$)$$. \ $displaystyle$ C_{1$}$ $:$ $( x$_ {1} ( t ) , y$_ {$1} ( t ) , \ $C_{$2 ( $x _$ { 2 ($s$) ） 。$}$

두 변수를 같게 하면 두 변수에서 두 개의 방정식이 생성됩니다.

${\displaystyle x_{1}(t)=x_{2}(s),\y_{1}(t)=y_{2}(s)\ .}$

• 한 곡선이 파라미터로 지정되고 다른 곡선이 암묵적으로 지정되는 경우: ${\displaystyle {C\mathrm{}}_{}}$1${\displaystyle }$: ( ${\displaystyle {}_{}{1\mathrm{}}_{}}$ (${\displaystyle t}$) , ${\displaystyle {y\mathrm{}}_{}}$1 (${\displaystyle t}$) , ${\displaystyle \text{C}{}_{}{2\mathrm{}}_{}}$ :${\displaystyle f}$ (${\displaystyle x}$ ,${\displaystyle y}$ ) ${\displaystyle =0}$. \ $displaystyle C_{1} ( t$ ) , y _ { 1 ( t ) , \ C _ $2 : f$ ,$y$ ) $=$$0$ .$}$

이것은 명백한 경우를 제외하고 가장 간단한 경우이다.$(\$ C_${$$2})$의 공식 $f{\displaystyle (x,}$ ${\displaystyle y)}$ $=$(\$displaystyle$ f$(x,y$)=$0)$에 $(\$${$1$})$의 파라메트릭 표현을 삽입하면 다음과 같은 식을 얻을 수 있습니다.

${\displaystyle f(x_{1}(t),y_{2}(t)=0\.}$

• 두 곡선이 암묵적으로 주어지는 경우: ${\displaystyle {C\mathrm{}}_{}}$1 : ${\displaystyle {}_{}{1\mathrm{}}_{}}$ (${\displaystyle x}$ ,${\displaystyle y}$ ) ${\displaystyle =0}$ , ${\displaystyle {C\mathrm{}}_{}}$2 : $2$ (${\displaystyle x}$ ,${\displaystyle y}$ ) ${\displaystyle =0}$. \ $displaystyle C_{1$} (x$$,$$y ) =$0$, \ $C_{2$} : $f_{$2} (x , y ) $=$ 0 .$}$

여기서, 교차점은 시스템의 해결책입니다.

${\displaystyle f_{1}(x,y)=0,\f_{2}(x,y)=0\.}$

모든 뉴턴 반복에는 편리한 시작 값이 필요하며, 이는 두 곡선의 시각화를 통해 도출될 수 있습니다.파라메타 t 또는 x 각각에 대해 대응하는 점을 산출하기 쉽기 때문에 파라메타적으로 또는 명시적으로 주어진 곡선을 쉽게 가시화할 수 있다.암묵적으로 주어진 곡선의 경우 이 작업은 쉽지 않습니다.이 경우 시작 값과 반복을 사용하여 곡선 점을 결정해야 합니다.를 ^[2]참조해 주세요.

예:

1 : $C{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$:${\displaystyle }$(${\displaystyle t}$ , ${\displaystyle {t\mathrm{}}^{}}$3$$) ( { $displaystyle C_{1$} : ($t$ , $t^{3}$ ) 및 C$$ ${\displaystyle {2\mathrm{}}_{}}$ :${\displaystyle }$(${\displaystyle x}$ -${\displaystyle {}^{}1}$)${\displaystyle {}^{}{2\mathrm{}}^{}}$+ (${\displaystyle y}$ -${\displaystyle {}^{}1}$)${\displaystyle {}^{}{2\mathrm{}}^{}{}_{}}$- ${\displaystyle 10}$ ${\displaystyle =}$0 ( \ $displaystyle C_{2}$+ ( x-1)^$2 - 10 =$ 0 ($그림$ 참조$)$

뉴턴 $반복{\displaystyle {}_{}}$ ${\displaystyle t_{}}$n +${\displaystyle 1_{}}$ : $=$ ${\displaystyle {}_{}{n}_{}}$ -${\displaystyle \frac{}{}f\frac{}{}}$ ( ${\displaystyle \frac{t_{}}{}}$n ) f$f$ ( ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{n_{}}{}}$){$displaystyle t_${n$+1}:= t_{n}-{\frac {f(t_{n}}}{f$$'(t_{n}}}}}}}}:$

${\displaystyle f}$(${\displaystyle t}$ ) $=$ (${\displaystyle t}$ -${\displaystyle {}^{}1}$ )${\displaystyle {}^{}{2\mathrm{}}^{}}$+ ( ${\displaystyle {t\mathrm{}}^{}{}^{}}$3 -${\displaystyle {}^{}1}$)${\displaystyle {}^{}}$2 - ${\displaystyle 10}$ ${\displaystyle$ f$(t$)=($t-1)^{2}+(t^{3}-1)^{2}-10}$을 수행해야 합니다.시작 값으로 -1과 1.5를 선택할 수 있습니다.

교차점은 다음과 같습니다(-1.1073, -1.3578). (1.6011, 4.1046)

${\displaystyle {2\mathrm{}}_{}}$: C${\displaystyle {}_{}}$1 : ${\displaystyle {}_{}{1\mathrm{}}_{}}$ (${\displaystyle x}$ ,${\displaystyle y}$ ) ${\displaystyle =}$ ${\displaystyle {x\mathrm{}}^{}}$4 + ${\displaystyle {}^{}{4\mathrm{}}^{}}$ - ${\displaystyle 1}$ ${\displaystyle =0}$, { $displaystyle C_{1}(x,y$)=$x^{4}+y^{4}-1=0,}$

${\displaystyle {C\mathrm{}}_{}}$2 : ${\displaystyle {f\mathrm{}}_{}}$2 (${\displaystyle x}$ ,${\displaystyle }$y ) ${\displaystyle =}$ (${\displaystyle x}$ -${\displaystyle 0.5{}^{}}$)${\displaystyle {}^{}{2\mathrm{}}^{}}$+ (${\displaystyle y}$ - 0.${\displaystyle 5{}^{}}$)${\displaystyle {}^{}{2\mathrm{}}^{}}$ - ${\displaystyle 1}$ $0$ ( { $display$C _ {2$}$ $( x$ , y ) = ( x , $y )^2}$ + ( $y$- 0.5 )^2 -$1$=$0$（$$ y - 0.5 $） 。$

뉴턴 반복

${\displaystyle (}$ ${\displaystyle \genfrac{}{}{0ex}{}{x_{}}{}\genfrac{}{}{0ex}{}{n_{}}{}}$ + ${\displaystyle \genfrac{}{}{0ex}{}{1_{}}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{{}_{}}{{}_{\mathrm{n}}}}$ +${\displaystyle \genfrac{}{}{0ex}{}{{}_{}}{}}$1 ) ${\displaystyle =}$ ( ${\displaystyle x\genfrac{}{}{0ex}{}{{}_{}}{}}$${\displaystyle \genfrac{}{}{0ex}{}{{}_{}}{}}$n + ${\displaystyle \genfrac{}{}{0ex}{}{{}_{}}{{}_{}}}$ y${\displaystyle \genfrac{}{}{0ex}{}{{}_{}{n}_{}}{}}$ + $δdeltay$ ${\displaystyle \genfrac{}{}{0ex}{}{{}_{}}{}}${ $displaystyle$ {$x _ { n$ +$1$} \ $choose$ y $_$ ${ x n$ } + \ $choose$y _ { $y$${\displaystyle \genfrac{}{}{0ex}{}{{}_{}}{}}$} $=$${\displaystyle }${ ${\displaystyle \genfrac{}{}{0ex}{}{x_{}}{}}$$${ ${\displaystyle \genfrac{}{}{0ex}{}{n_{}}{}}$$$} + \ $choose$ y _ { $display } styledisplay$_ {$n }$ )

(f1∂ ∂)f는 y∂ f2∂ 1∂ x∂ f2∂ ∂ y)(δ)δ y))(f1− f2−){\displaystyle{\begin{pmatrix}{\frac{\partial f_{1}}{x\partial}}&{\frac{\partial f_{1}}{이\partial}}\\{\frac{\partial f_{2}}{x\partial}}&,{\frac{\part.ial f_{2$}{\display y}}\end${pmatrix$}{\display _{x}\choose _{y}={-f_{1$}\$choose -f_{$2}}${\displaystyle {}_{}}$(x n,${\displaystyle {}_{}{y}_{}}$n){$displaystyle$ ($x_{n$},$y_{$n$\}\})$에서 시작값으로 0.5, 1 및 (1, 0.5)를 선택할 수 있습니다.

선형 시스템은 크레이머의 법칙으로 풀 수 있다.

교차점은 (-0.3686, 0.9953) 및 (0.9953, -0.3686)입니다.

2개의 폴리곤

두 폴리곤의 교차점을 결정하려면 폴리곤의 선분 쌍이 교차하는지를 확인할 수 있습니다(위 참조).세그먼트가 많은 폴리곤의 경우 이 방법은 다소 시간이 걸립니다.실제로 윈도우 테스트를 사용하여 교차 알고리즘을 가속합니다.이 경우 폴리곤을 작은 하위 폴리곤으로 나누고 하위 폴리곤에 대해 가장 작은 창(좌표 축에 평행한 변과 직각)을 결정합니다.두 선분의 교차점 결정을 시작하기 전에 모든 윈도우 쌍이 공통점에 대해 테스트됩니다.보세요.^[3]

공간 내(3차원)

3차원 공간에서는 곡선과 표면 사이에 교차점(공통점)이 있습니다.다음 섹션에서는 횡단 교차로만 고려합니다.

선과 평면

선과 평면이 3차원에서 일반 위치에 있는 교차점은 점입니다.

일반적으로 공간의 선은 파라메트릭(${\displaystyle x}$(${\displaystyle t}$) ,${\displaystyle y}$ (${\displaystyle t}$) ,${\displaystyle z}$ (${\displaystyle t}$) $){ display$ ($x$ ( x ($t$ ) ,$y$ ($t$ ) ,$z$ ($t$ )}}}}} $and$ a a a 평면을 a${\displaystyle }$+ ${\displaystyle b}$y + ${\displaystyle c}$ z ${\displaystyle =}$ \ $display style$ + $by$+$cz = d$} )로 나타냅니다.파라메트릭 표현을 방정식에 삽입하면 선형 방정식이 생성됩니다.

${\displaystyle ax(t)+by(t)+cz(t)=d\,}$

$({\displaystyle }$ $x{\displaystyle {}_{}}$${\displaystyle }$( ${\displaystyle {}_{}{0\mathrm{}}_{}}$) ,${\displaystyle }$$y$ (${\displaystyle {}_{}}$) ,${\displaystyle z}$ ( ${\displaystyle {t\mathrm{}}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ) , z ( ${\displaystyle {}_{}}$0 )${\displaystyle }$\ $displaystyle ( x$ ( t$_$ 0 )$$,$y$ ( t_${0}$ ) , y ( $t_$${$0$$} , z ( $t_{0}$ )$$$。$

선형 방정식에 해답이 없는 경우 선은 평면에 있거나 평면에 평행합니다.

3면

선이 두 개의 교차 평면 ${\displaystyle i_{}\text{i}{\stackrel{}{}}_{}}$ : n ${\displaystyle {\stackrel{}{\to }}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle x\stackrel{}{}}$ x ${\displaystyle \to }$ ${\displaystyle {di}_{}}$ ${\displaystyle {}_{}}$ i ${\displaystyle =}$ ${\displaystyle 1}$, ${\displaystyle 2}$ \ $display \ varepsilon$_ { $i }$ \ $cdot$ {$x } = d_${ i } , \ i$$= i = ${\displaystyle i_{\mathrm{}}}$$→$ ${\displaystyle {3d\mathrm{}}_{}}$ 평면${\displaystyle {}_{}{}_{}}$ ${\displaystyle d2\stackrel{}{}}$ ${\displaystyle \text{di<img alt="varepsilon\_i: vec n\_icdotvec x=d\_i, i=1,2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/b5dc7ada2c35c8c9fe302c4258fc4622bff07daf" style="vertical-align: -0.671ex; width:23.586ex; height:2.676ex;">}{\stackrel{}{}}_{}}$ :$ot {vec {x}}=d_{3$ 세 평면의 공통 교차점을 평가해야 한다.

선형 독립 법선 $벡터{\displaystyle {\stackrel{}{}}_{}}$ n${\displaystyle {\stackrel{}{=}}_{}}$ 1,${\displaystyle 2}$, ${\displaystyle 3}$${\displaystyle {}_{}{\stackrel{}{}}_{}}$ $스타일 \varepsilon$ _${i})\cdot$ {$vec$ {$x}=$${\displaystyle {\stackrel{}{}}_{}}$${i},$ \$i=$${\displaystyle 1_{\mathrm{}}}$, 2$, 3$$)$의 세 ${\displaystyle {평면}_{}\text{display}{\stackrel{}{}}_{}}$ ${\displaystyle n_{}{\stackrel{}{\to }}_{}}$ ${\displaystyle {di}_{}}$、 n ${\displaystyle \to }$${\displaystyle {}_{}}$di 、 n 、 $display$ ${\displaystyle {\stackrel{}{\to }}_{}}$ ${\displaystyle 3_{\mathrm{}}}$온 포인트로

${\displaystyle {p}_{0}=bec frac {d_{1}({\vec {n}_{2}\times {vec {n}}_{3}\times {vec {n})+d_{2}({1}+d_3}\times {vec {c}{c})$

증명을 위해 n → i ${\displaystyle {\stackrel{}{}}_{}}$ p ${\displaystyle {\stackrel{}{\to }}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {di}_{}}$ ${\displaystyle \text{i}}$ ${\displaystyle =1}$,${\displaystyle 2}$,${\displaystyle }$3$$, {$displaystyle {vec {n}_{i}\cdot {d_{i},\i=1,$2$, 3}$을 스칼라 삼중곱의 법칙을 사용하여 $설정$해야 한다.스칼라 삼중곱이 0이면 평면에는 삼중 교차가 없거나 선(또는 세 평면이 모두 같은 경우 평면)입니다.

곡선과 표면

평면 케이스와 유사하게 다음과 같은 경우 비선형 시스템으로 이어지며, 1차원 또는 3차원 ^[4]뉴턴 반복을 사용하여 해결할 수 있습니다.

• $파라메트릭{\displaystyle }$곡선${\displaystyle C}$: (${\displaystyle x}$( ${\displaystyle t}$) ,${\displaystyle y}$( t${\displaystyle }$) , z (${\displaystyle t}$) \ $displaystyle C$ : ($x$ ( $t$) ,$y$ ( $t$$)$ } } 。

파라메트릭 $서페이스{\displaystyle }$S${\displaystyle }$: (${\displaystyle x}$ (${\displaystyle u}$ ,${\displaystyle v}$) ,${\displaystyle y}$ (${\displaystyle u}$ ,${\displaystyle }$v${\displaystyle }$) ,${\displaystyle z}$ (${\displaystyle u}$ ,${\displaystyle }$v${\displaystyle }$)$$, \ $display style$ S : ( $x ( u$ , v ) , $y ( u$ , v ) ,$z$ ($u$ , v ) \ ,$$}

• $파라메트릭{\displaystyle }$곡선${\displaystyle C}$: (${\displaystyle x}$( ${\displaystyle t}$) ,${\displaystyle y}$( t${\displaystyle }$) , z (${\displaystyle t}$) \ $displaystyle C$ : ($x$ ( $t$) ,$y$ ( $t$$)$ } } 。

암묵적 $표면{\displaystyle }$S :${\displaystyle f}$ (${\displaystyle x}$ ,${\displaystyle y}$ ,${\displaystyle z}$ ) $=$. { $displaystyle$ S$:f (x , y$ , z )=$0$ \$$}

예:

파라메트릭${\displaystyle }곡선{\displaystyle C}$: ( ${\displaystyle {}^{}}$ , ${\displaystyle {t\mathrm{}}^{}}$2, ${\displaystyle {t\mathrm{}}^{}}$3$$) { $displaystyle$ C $:$ ( t , t$^ {2$} , t^ {3$}$} ,

암묵적 $표면{\displaystyle }$S : ${\displaystyle {x\mathrm{}}^{}{}^{}}$ +${\displaystyle {}^{}{y\mathrm{}}^{}}$ 4 +${\displaystyle {}^{}{z\mathrm{}}^{}}$ ${\displaystyle 4}$ - ${\displaystyle 1}$ $=$ 0 {\ $displaystyle S:x$^{$4}+y^{4}+z^{4}-1=0}($s. 그림).

교차점은 (-0.8587, 0.7374, -0.6332), (0.8587, 0.7374, 0.632)입니다.

선-구 교차로는 단순한 특수한 경우입니다.

선이나 평면의 경우와 마찬가지로 곡선과 일반 위치의 서페이스의 교점은 이산점으로 구성되지만 곡선은 서페이스에 일부 또는 전체를 포함할 수 있다.

선과 다면체

양면

횡단적으로 교차하는 두 지표면이 교차 곡선을 제공합니다.가장 단순한 경우 두 평행하지 않은 평면의 교차선입니다.

「 」를 참조해 주세요.

• 해석 지오메트리 #교차로
• 계산기하학
• 직선의 방정식
• 교차로(집합 이론)
• 교차 이론

레퍼런스

추가 정보

• Nicholas M. Patrikalakis와 Takashi Maekawa, 컴퓨터 보조 설계 및 제조를 위한 형상 질문, Springer, 2002, ISBN3540424547, 9783540424543, 페이지 408. [1]