커널(통계)
Kernel (statistics)이 글은 검증을 위해 인용구가 추가로 필요하다.– · · 책· · (2012년 5월)(이 |
커널이라는 용어는 통계 분석에서 창 함수를 지칭하기 위해 사용된다. "커널"이라는 용어는 다른 통계 분기에 몇 가지 뚜렷한 의미를 가지고 있다.
베이지안 통계
특히 베이시안 통계에서 확률밀도함수(pdf)나 확률질량함수(pmf)의 커널은 도메인 내 변수의 함수가 아닌 모든 요인이 생략된 pdf 또는 pmf의 형태다.[citation needed] 이러한 요인은 pdf 또는 pmf 매개변수의 함수일 수 있다는 점에 유의하십시오. 이러한 요인은 확률 분포의 정규화 요인의 일부를 형성하며, 많은 상황에서 불필요하다. 예를 들어 의사 난수 샘플링에서 대부분의 샘플링 알고리즘은 정규화 계수를 무시한다. 또한, 결합 이전 분포의 베이지안 분석에서는 계산 중에 정규화 인자는 일반적으로 무시되며, 커널만 고려된다. 마지막에 낟알의 형태를 검사하고, 알려진 분포와 일치하면 정상화 인자를 회복할 수 있다. 그렇지 않으면 불필요할 수 있다(예를 들어, 분포만 표본 추출하면 되는 경우).
많은 분포의 경우, 커널은 닫힌 형태로 작성할 수 있지만 정규화 상수는 작성할 수 없다.
그리고 관련 커널은
지수 앞 인자는 도메인 변수 의 함수가 아니기 때문에 2 를 포함함에도 불구하고 생략되었다는 점에 유의하십시오.
패턴분석
재생성 커널 힐버트 공간의 커널은 커널 메소드라고 알려진 기법의 집합에서 사용되어 암묵적 공간의 데이터에 대한 통계 분류, 회귀 분석, 클러스터 분석 등의 작업을 수행한다. 이러한 용법은 특히 기계학습에서 흔하다.
비모수 통계량
비모수 통계량에서 커널은 비모수 추정 기법에 사용되는 가중 함수다. 커널은 랜덤 변수의 밀도 함수를 추정하기 위해 커널 밀도 추정에, 또는 랜덤 변수의 조건부 기대치를 추정하기 위해 커널 회귀 분석에 사용된다. 또한 커널은 윈도우 함수로 알려진 스펙트럼 밀도를 추정하기 위해 주기그램을 사용하는 시계열에도 사용된다. 윈도우 기능(커널)이 시계열 데이터로 컨버전스되는 포인트 프로세스에 대한 시간 변동 강도를 추정할 때 추가적으로 사용된다.
일반적으로 커널 너비는 비모수 추정을 실행할 때도 지정해야 한다.
정의
커널은 음이 아닌 실질가치의 통합함수 K이다. 대부분의 애플리케이션의 경우, 다음의 두 가지 추가 요건을 충족하도록 함수를 정의하는 것이 바람직하다.
- 정규화:
- 대칭:
첫 번째 요건은 커널 밀도 추정 방법이 확률 밀도 함수를 초래한다는 것을 보장한다. 두 번째 요건은 해당 분포의 평균이 사용된 표본의 평균과 동일함을 보장한다.
K가 커널이라면 K*(u) = λK(λu)에 의해 정의된 K*함수 K*도 여기서 λ > 0이다. 데이터에 적합한 척도를 선택하는 데 사용할 수 있다.
커널 함수의 공통 사용
여러 종류의 커널 함수가 일반적으로 사용된다: 균일, 삼각, 에판치니코프,[1] 쿼트릭(비급), 트리큐브,[2] 트라이웨이트, 가우스, 2차[3], 코사인.
아래 표에서 이(가) 경계 지지대로 주어지면 지지대 외부에 놓여 있는 u의 값에 K )= 이(가) 된다.
| 커널 함수, K(u) | Epanechnikov 커널에 대한 효율성[4] | ||||
|---|---|---|---|---|---|
| 균일("사각형 창") | 지원: |  "박스카 기능" | 92.9% | ||
| 삼각형 | 지원: | 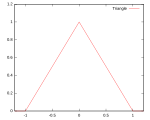 | 98.6% | ||
| 에판치니코프 (패러볼릭) | 지원: |  | 100% | ||
| 사분위수 (비급) | 지원: | 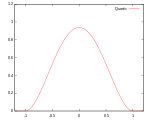 | 99.4% | ||
| 트라이급 | 지원: |  | 98.7% | ||
| 트리큐브 | 지원: |  | 99.8% | ||
| 가우스어 | 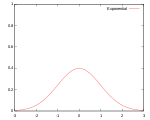 | 95.1% | |||
| 코사인 | 지원: | 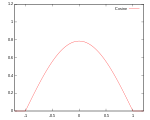 | 99.9% | ||
| 로지스틱 |  | 88.7% | |||
| 지그모이드 함수 |  | 84.3% | |||
| 실버맨 커널[5] |  | 해당되지 않는 | |||
참고 항목
참조
- ^ 에 대해 명명됨 Epanechnikov, V. A. (1969). "Non-Parametric Estimation of a Multivariate Probability Density". Theory Probab. Appl. 14 (1): 153–158. doi:10.1137/1114019.
- ^ Altman, N. S. (1992). "An introduction to kernel and nearest neighbor nonparametric regression". The American Statistician. 46 (3): 175–185. doi:10.1080/00031305.1992.10475879. hdl:1813/31637.
- ^ Cleveland, W. S.; Devlin, S. J. (1988). "Locally weighted regression: An approach to regression analysis by local fitting". Journal of the American Statistical Association. 83 (403): 596–610. doi:10.1080/01621459.1988.10478639.
- ^ 은 u u uu u u u u u u u u u u u uu u u u u u u u u u u u u u u u u u u u u u 2 d u u u u u u u u
- ^ Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis. Chapman and Hall, London.
- Li, Qi; Racine, Jeffrey S. (2007). Nonparametric Econometrics: Theory and Practice. Princeton University Press. ISBN 978-0-691-12161-1.
- Zucchini, Walter. "APPLIED SMOOTHING TECHNIQUES Part 1: Kernel Density Estimation" (PDF). Retrieved 6 September 2018.
- Comaniciu, D; Meer, P (2002). "Mean shift: A robust approach toward feature space analysis". IEEE Transactions on Pattern Analysis and Machine Intelligence. 24 (5): 603–619. CiteSeerX 10.1.1.76.8968. doi:10.1109/34.1000236.














































