호모테틱 중심

기하학에서 동음이의 중심(유사성의 중심 또는 유사도의 중심이라고도 함)은 적어도 두 개의 기하학적으로 비슷한 형상이 서로 팽창하거나 수축하는 것으로 볼 수 있는 지점이다. 중심이 외부일 경우 두 수치는 서로 직접 유사하며 각도는 동일한 회전 감각을 가진다. 중심이 내부일 경우, 두 도형은 서로 거울에 비친 눈금이다. 각도는 정반대의 감각을 가지고 있다.

일반 다각형

두 기하학적 형상이 동음이의 중심점을 가지고 있다면 서로 유사하다. 즉, 두 기하학적 형상은 해당 지점에서 동일한 각도를 가져야 하며 상대적 스케일링에서만 차이가 난다. 동음이의 중심과 두 형상은 같은 평면에 있을 필요가 없다; 동음이의 중심에서 돌출된 것에 의해 연관될 수 있다.

동음이의 중심은 외부 또는 내부일 수 있다. 중심부가 내부일 경우 두 기하학적 형상은 서로 거울에 비친 눈금이다. 기술적 언어로 그들은 서로 반대되는 음향을 가지고 있다. 한 그림에서 시계방향 각도는 다른 그림에서 시계 반대방향 각도와 일치할 것이다. 반대로 중심이 외부인 경우 두 수치는 서로 직접적으로 유사하다; 각도는 같은 감각을 가지고 있다.

서클

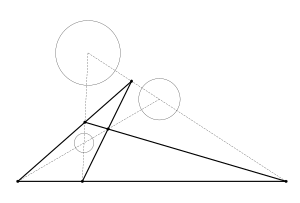
원은 기하학적으로 서로 유사하며 대칭으로 거울을 비춘다. 따라서 한 쌍의 원은 중심이 같거나 반지름이 같지 않은 한 내부와 외부의 동음이의 중심 두 가지 유형을 모두 가지고 있다. 이러한 예외적인 경우는 일반 위치 이후에 처리된다. 이 두 개의 동음이의 중심은 주어진 두 원의 중심과 연결되는 선에 놓여 있는데, 이를 중심선이라고 한다(그림 3). 반지름이 0인 원도 포함될 수 있으며(예외 사례 참조), 음의 반지름도 사용할 수 있어 외부와 내부를 전환할 수 있다.

동음이의학 센터 계산

주어진 한 쌍의 원의 경우, 내외부의 동음이의 중심은 다양한 방법으로 발견될 수 있다. 해석 기하학에서 내부 동심 중심은 원의 중심에서 가중 평균으로, 반대 원의 반지름에 의해 가중치가 부여된다. 원의 중심에서 내부 중심까지의 거리는 반경에 비례하므로 가중치는 반대 반경에 비례한다. Denoting the centers of the circles ${\displaystyle C_{1}}$ and ${\displaystyle C_{2}}$ by ${\displaystyle (x_{1},y_{1})}$ and ${\displaystyle (x_{2},y_{2})}$ and their radii by ${\displaystyle r_{1}}$ and ${\displaystyle r_{2}}$ and deno$({\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}{}_{}}$ ${\displaystyle {y\mathrm{}}_{}}$ 0 )${\displaystyle }$, ${\displaystyle(x_{0},y_{0}),}$이(가) 다음을 기준으로 한다.

${\displaystyle (x_{0},y_{0}}={\frac {r_{1}{1}{1}{1}}(x_{1},y_{1}})+{\frac {r_{1}{1}{1}{1}}}}(x_{2},y_{2})}}$

외부 중심은 동일한 방정식으로 계산할 수 있지만, 반지름 중 하나를 음수로 간주한다. 둘 중 하나는 동일한 방정식을 산출한다. 즉, 다음과 같다.

${\displaystyle (x_{e},y_{e}}={\frac {-r_{1}-{1}-{1}}}(x_{1},y_{1}})+{\frac {r_{1}{1}-{1}-{1}}}}(x_{2},y_{2}).}$

보다 일반적으로 같은 부호(양수 또는 음수 모두)로 두 반지름을 취하면 내측 중심이 되고, 반대 기호(양수 하나와 음수 둘 다)로 반경을 취하면 외측 중심이 된다. 내부 중심에 대한 방정식은 어떤 값에도 유효하지만(반경 0 또는 한 값이 다른 값의 음이 아닌 경우), 외부 중심에 대한 방정식은 반경이 다를 것을 요구하고, 그렇지 않으면 0으로 나누어야 한다는 점에 유의한다.

합성 기하학에서는 각 원마다 하나씩 두 개의 평행 직경이 그려진다; 이것들은 중심선과 동일한 각도 α를 만든다. 동음이의 점인 이 반지름의 해당 끝점을 통해 그려진 AA와₁₂ BB₁₂ 선은 서로 교차하며 외부 동음이의 중심선이다. 반대로, 한 끝점과 반대 끝점을 통해 그려진 AB₁₂ 선과 BA₁₂ 선은 서로 교차하며, 내부 동음이의 중심선에 중심선이 교차한다.

이 구조의 제한적 사례로서, 두 원(비탄젠트 선)에 접하는 선은 동음이의 중심 중 하나를 통과하는데, 이는 두 직경과 직각을 형성하기 때문에, 따라서 평행이다. 자세한 내용은 두 원의 접선 선을 참조하라. 원들이 선의 반대편에 떨어지면 위 그림의 AB와₂₁ 같이 내부 동음이의 중심부를 통과한다. 반대로 원들이 선의 같은 면에 떨어지면 외부 동음이의 중심(사진은 아님)을 통과한다.

특례

원의 반지름(그러나 중심은 서로 다른 경우)이 있는 경우 부속 평면에 외부 동음이의 중심은 없다: 분석 기하학에서는 0으로 분할되는 반면, 합성 $기하학$에서는 A$$ 1 ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$2}} 및 $B{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ B ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 스타일 $B_{1}B_{2$}} 선은 c의 선과 평행하다$$.(차선 및 이항선 둘 다)를 입력하므로 교차가 없다. 외부 중심은 투영 평면에서 이 선의 기울기에 해당하는 무한대의 점으로 정의할 수 있다. 원의 중심이 고정되고 반지름이 같을 때까지 변화하면 이 또한 외부 중심부의 한계다.

원의 중심은 같지만 반지름은 다를 경우, 외부와 내부 모두 원의 공통 중심과 일치한다. 이는 분석 공식에서 알 수 있으며, 두 원의 중심이 일치할 때까지 변화하여 반지름을 균일하게 유지하므로 두 개의 동음이의 중심에서 한계이기도 하다. 그러나 중앙선은 없고, 두 평행선이 일치하면서 합성구축은 실패한다.

한 반지름이 0이지만 다른 반지름이 0이 아닌 경우(점 및 원) 외부 중심과 내부 중심은 모두 점(반경 제로 원의 중심)과 일치한다.

두 원(동일한 중심, 동일한 반지름)이 동일한 경우, 내부 중심은 공통 중심이지만 외부 중심은 잘 정의되지 않은 경우 – 적절하게 평면에 있는 두 원의 매개변수 공간에서 외부 중심까지의 함수는 동일한 원의 중심부에 비이동성 불연속성을 가진다. 반경은 같지만 뚜렷한 중심이 같은 중심을 갖는 두 원의 한계에서 외부 중심은 중심선의 기울기에 해당하는 무한대의 지점이며, 이는 무엇이든 될 수 있기 때문에 그러한 원의 모든 쌍에 대한 한계는 존재하지 않는다.

반대로 두 반지름 모두 0(2점)이지만 점이 구별되는 경우, 외부 중심은 중심선의 기울기에 해당하는 무한대의 점으로 정의할 수 있지만 내부 중심은 잘 정의되어 있지 않다.

호몰로직 및 반호몰로직 포인트

일반적으로 동음이의 중심에서 뿜어져 나오는 광선은 각각의 원을 두 곳에서 교차하게 된다. 이 네 점 중 두 점은 그림 4의 점 Q와 Q′와 같이 중심을 연결하는 선과 동일한 각도를 이루는 경우 동음이의어라고 한다. 동음이의 중심과 관련하여 선명한 점이지만 동음이의어가 아닌 점은 그림 4의 점 Q와 P와 같은 ^[1]반호몰로코성이라고 한다.

반동맥 점 쌍이 원 위에 놓여 있다.

같은 동음이의 중심에서 나온 두 개의 광선이 원과 교차할 때, 각각의 반동음이의 점들이 원 위에 놓여진다.

EQS 및 EQ andS′ 삼각형을 고려한다(그림 4).
공유 각도 ∠QES=∠Q′ES′과 ${\displaystyle \frac{\mathrm{EQ}}{}}$ E ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{\prime \mathrm{}}^{}}{}}$= ${\displaystyle E\frac{}{}}$ ${\displaystyle \frac{S}{}}$ ${\displaystyle \frac{}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{\prime \mathrm{}}^{}}{}}$ ${\$$EQ^{\prime }}={\frac {ES}{ES^{\prime }}}$E는 동음이의 중심이므로. 그 유사성으로부터 【ESQ=】가 뒤따른다.ES′Q′=α. 새겨진 각도 정리 ∠.EP′R′=∠ES′Q′. ∠QSR′=180°-α는 ∠ESQ에 보충되어 있기 때문이다. 4면체 Q에서SR′P′ ∠QSR′+∠QP′R′=180°-α+α=180°는 원 안에 새겨질 수 있다는 뜻이다. 세컨트 정리로부터 그 EQ를 따른다.EP′=ES·ER′.

같은 방법으로 PRS′Q′은 원과 EP로 새겨질 수 있음을 보여줄 수 있다.EQ′=ER·ES′.

그 증거는 내부 동음이의학 센터 I과 비슷하다.
PIR~PHIR′ 다음에 ∠RPI=∠IP′R′=α. ∠RS′Q′=∠PP′R′=α(속칭 각도 정리) 세그먼트 RQ′은 R, P, S′, Q′가 원 위에 놓여 있다는 뜻의 P와 S′로부터 동일한 각도로 보인다. 교차하는 화음 정리로부터IP·IQ′=IR·IS′. 유사하게 QSPrR′은 원과 IQ로 새겨질 수 있다.IP′=IS·IR′.

과격축과의 관계

두 원은 급진적인 축을 가지고 있는데, 이것은 두 원과의 접선이 길이가 같은 점의 선이다. 보다 일반적으로, 급진축의 모든 점들은 원과 관련된 힘이 동등하다는 속성을 가지고 있다. 급진축은 항상 중심선과 직각이며, 두 원형이 교차하면 그들의 급진축은 교차점을 잇는 선이다. 3개의 원에 대해 각 원 쌍(C₁/C₂, C₁/C₃, C₂/C₃)에 대해 3개의 급진적 축을 정의할 수 있으며, 놀랍게도 이들 3개의 급진적 축은 하나의 지점, 즉 급진적 중심에서 교차한다. 급진적인 중심에서 세 원까지 끌어온 접선은 모두 길이가 같을 것이다.

어떤 두 쌍의 항호몰로지 점을 사용하여 급진축에서 점을 찾을 수 있다. 그림 4의 외부 동심 중심 E에서 방출되는 두 개의 광선을 고려하십시오. 이러한 광선은 두 쌍의 반동맥 점(그림 4의 녹색과 청색)으로 주어진 원(첫 번째 광선의 경우 Q와 P ray, 두 번째 광선의 경우 S와 R′)을 교차한다. 이 네 점은 주어진 원과 교차하는 하나의 원 위에 놓여 있다. 정의에 따르면 QS 선은 녹색 주어진 원을 가진 새로운 원의 급진적인 축인 반면 PrR the 선은 파란색 주어진 원을 가진 새로운 원의 급진적인 축이다. 이 두 선은 새로운 원과 주어진 원 두 개의 급진적인 중심인 G 지점에서 교차한다. 따라서 G 지점도 주어진 두 원의 급진적 축에 놓여 있다.

접선 원 및 반호몰로지 점

두 원의 각 쌍에 대해 주어진 원과 접하고 반원점에서 그것들을 만지는 세 번째 원이 존재한다.
그 반대도 사실이다. 다른 두 원과 접하는 모든 원은 한 쌍의 반호몰로게이션 포인트에서 그것들에 닿는다.

우리 두 원은 중심 O와 중심₁ O를₂ 갖도록 하자(그림 5). E는 그들의 외부 동음이의 중심이다. 우리는 P, Q, P, Q의 두 원과 교차하는 E로부터 임의의 광선을 구성한다. OQ와₁ OPT가₂ T에서₁ 교차할 때까지 연장한다. 동음이의어 때문에₁ 삼각형 OPQ와 OP₂′Q′가 유사하다는 것은 쉽게 증명된다. They are also isosceles because O₁P=O₁Q (radius), therefore ∠O₁PQ=∠O₁QP=∠OP₂′Q′=∠OQ₂′P′=∠∠T₁QP′=∠T₁P′Q. 따라서 TP₁′Q도 등각이며 중심 T와₁ 반지름 TP₁′=TQ로₁ 원을 구성할 수 있다. 이 원은 Q 지점과 P 지점에서 주어진 원 2개에 접한다.

내부 동음이의 중심부의 경우뿐만 아니라 다른 쌍의 반동음이의 점(P와 Q′)에 대한 증명은 유사하다.

만약 우리가 가능한 모든 쌍의 반동맥 점들에 대해 접선 원들을 구성한다면, 우리는 두 개의 동그라미를 얻게 된다. 각 동음이의 중심마다 하나씩. 외부 동심원의 원군은 모든 접선 원은 주어진 원을 포함하거나 포함하지 않을 수 있다(그림 6). 반면에 다른 가족의 원은 항상 주어진 원 중 하나만 포함하고 있다(그림 7).

접선가족의 모든 원은 공통적인 급진적 중심을 가지고 있으며 동음이의 중심과 일치한다.
이를 나타내려면 주어진 원을 교차하는 동음이의 중심에서 두 개의 광선을 고려하십시오(그림 8). 두 개의 접선 원 T와₁ T가₂ 존재하며, 두 개의 접선 원은 반호몰로직 지점에서 주어진 원과 접촉한다. 우리가 이미 보여드린 바와 같이 이 점들은 원 C에 놓여있으며 따라서 두 개의 광선은 C/T와₁ C/T를₂ 위한 급진적인 축이다. 그렇다면 두 급진축의 교차점 역시₁ T/T의₂ 급진축에 속해야 한다. 이 교차점은 동음이의 중심 E이다.

두 개의 접선 원이 그림 5와 같이 반호몰로코 포인트의 콜린어 쌍을 터치하는 경우 ${\displaystyle \frac{{}^{}}{}}$ E P${\displaystyle \frac{{\mathrm{}}^{}}{}}$E${\displaystyle \frac{{}^{}}{}}$P ${\displaystyle \frac{}{}}$ = E Q${\displaystyle \frac{{\mathrm{}}^{}}{}}$ Q${\displaystyle \frac{{}^{}}{}p;}$ E ${\displaystyle P}$ ${\displaystyle {=\mathrm{}}^{}}$ ${\displaystyle {}^{}}$Q q = E Q ${\displaystyle {}^{}}$ = E Q ′ E Q ${\displaystyle {\prime \mathrm{}}^{}}$ = E Q ${\displaystyle \prime }$ { { { { { ${$ {\$displaystytyle {\frictyleane{{{\flaysty}}{{$$EP^{\prime }}={\frac {EQ}{$$EQ^{\prime }};{EP}\cdot {EQ^{\premy }}={{{{{{}}}}}}$$EQ}\cdot {EP^{\prime$ $\}\}$ 따라서 두 접선 원에 대한 E의 힘은 같으며, 이는 E가 급진 축에 속함을 의미한다.

3개의 원의 동음이의 중심

원은 어느 한 쌍이라도 두 개의 유사성 중심이 있으므로, 세 개의 원은 각각 다른 한 쌍에 대해 두 개의 유사성 중심이 여섯 개 있을 것이다. 놀랍게도 이 여섯 점은 각 선에 세 점씩 네 줄에 놓여 있다. 이것을 보여주는 한 가지 방법이 있다.

세 개의 원의 평면을 고려한다(그림 9). 각 중심점을 해당 반지름과 동일한 거리로 평면에 수직으로 상쇄한다. 중심은 평면의 어느 한쪽으로 상쇄될 수 있다. 세 개의 간격띄우기 점은 단일 평면을 정의한다. 그 평면에서 우리는 각각의 점 쌍을 통해 세 개의 선을 만든다. 선은 H_AB, H_BC, H_AC 지점들에서 원의 평면을 관통한다. 두 개의 구별되고 평행하지 않은 평면에 공통적인 점의 중심은 선이기 때문에, 반드시 이 세 점이 그러한 선에 놓여 있다. 삼각형 HAA_AB′과 HBB_AB′의 유사성에서 우리는 $HA{\displaystyle \frac{{}_{}}{}}$ B ${\displaystyle \frac{{}_{}}{}}$ H ${\displaystyle \frac{{}_{}}{}}$= r ${\displaystyle \frac{{}_{}}{{}_{}}}$ ${\displaystyle \frac{r_{}}{}}$ ${\displaystyle \frac{A_{}}{}}$ ${\$$AB}B}{H_{$$AB}A}={\frac {r_{B}}{r_{{$$r_}}{{r_{{}}}$$A}}}($r는_A,B 원의 반지름)이고 따라서 H는_AB 사실 해당 두 원의 동음이의 중심이다. 우리는_BC H와 H도_AC 똑같이 할 수 있다.

서로 다른 동음이의 중심 조합에 대해 위의 절차를 반복하면(우리 방법에서 이것은 원의 중심을 상쇄하는 쪽에 의해 결정된다) 총 4개의 선이 생성될 것이다. 각 선에 세 개의 동음이의 중심이다(그림 10).

이것을 증명하는 또 다른 방법이 있다.

C와₁ C를₂ 주어진 원 세 개 모두에 접하는 원들의 결합 쌍이 되게 하라(그림 11). 결합에 의해 우리는 두 접선 원들이 주어진 원들 쌍들 중 어느 하나에 관해서도 같은 가족에 속한다는 것을 암시한다. 우리가 이미 보았듯이, 같은 가문 출신의 어느 두 접선 원의 급진적인 축은 주어진 두 원의 동음이의 중심부를 통과한다. 접선 원은 주어진 원의 세 쌍 모두에 공통적이기 때문에, 그들의 동음이의 중심은 모두₁ C와₂ C의 급진적인 축에 속하며, 예를 들어 그들은 한 줄에 놓여 있다.

이 재산은 아폴로니우스의 문제에 대한 요셉 디아즈 게르곤네의 일반적인 해결책에 이용된다. 세 개의 원을 볼 때 동음이의 중심은 찾을 수 있고 따라서 한 쌍의 솔루션 원의 급진적인 축을 찾을 수 있다. 물론 같은 급진축을 가진 원이 무한히 많기 때문에 정확히 어떤 두 개의 원이 해결책인지 알아내기 위해 추가 작업을 한다.

참고 항목

• 정리를 가로채다
• 유사성(지오메트리)
• 호모티컬 변환
• 과격축, 과격중심
• 아폴로니우스의 문제

참조