칸테레이션(기하학)
Cantellation (geometry)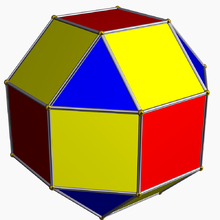
칸텔레이트 큐브 - 붉은 면이 감소합니다.가장자리가 사각형 모양으로 되어 있어 새로운 노란색 정사각형 면을 형성하고 있습니다.정점이 잘려서 새로운 파란색 삼각형 면을 형성합니다.
기하학에서 칸테레이션은 각 모서리와 정점에서 정규 폴리토프를 경사지게 하는 2차 자르기이며, 각 모서리와 각 정점 대신 새 패싯을 만듭니다.캔터레이션은 일반 타일링 및 벌집에도 적용됩니다.캔텔링 또한 그것의 정정을 바로잡고 있다.
칸테레이션(다면체와 타일링의 경우)은 Alicia Boole Stott에 의해 확장이라고도 불립니다.이것은 규칙적인 형태의 면을 중심에서 멀리 이동시키고 열린 각 모서리와 열린 정점에 대해 틈새에 새로운 면을 채우는 것에 해당합니다.
표기법
칸텔화 폴리토프는 확장 슐레플리 기호0,2 t{p,q,...로 나타난다.} 또는 { q..} { { {} p \ \ \ \ } 또는 rr{p,q,...}.
다면체의 경우 칸테레이션은 정다면체에서 그 쌍체까지의 직접 시퀀스를 제공합니다.
예: 입방체와 8면체 사이의 칸테레이션 시퀀스:
고차원 폴리토프의 경우, 칸테레이션은 정규 폴리토프에서 양방향 형태까지의 직접 시퀀스를 제공한다.
예: 다면체, 타일링 표시
| 형태 | 다면체 | 타일링 | |||
|---|---|---|---|---|---|
| 콕서터 | rTT | rCO | rID | rQQ | rHΩ |
| 콘웨이 표기법 | eT | eC = eO | eI = eD | eQ | eH = EΩ |
| 다면체 ~ 확대되다 | 사면체 | 큐브 또는 팔면체 | 이십면체 또는 12면체 | 정사각형 타일링 | 육각형 타일링 삼각 타일링 |
| 이미지 |  |  |  |  |  |
| 애니매이션 |  |  |  | ||
| 콕서터 | rrt{2,3} | rs{2,6} | rrco | RRID |
|---|---|---|---|---|
| 콘웨이 표기법 | eP3 | eA4 | eaO = eaC | eaI = eaD |
| 다면체 ~ 확대되다 | 삼각 프리즘 또는 삼각 이원체 | 정사각형 반체제 또는 정방정삼면체 | 정육면체 또는 마름모꼴 12면체 | 이십이면체 또는 마름모꼴 삼면체 |
| 이미지 |  |  |  |  |
| 애니매이션 |  |  |
「 」를 참조해 주세요.
레퍼런스
- Coxeter, H.S.M. Regular Polytopes, (3판, 1973년), Dover판, ISBN0-486-61480-8 (p.145-154 제8장: 잘라내기, 페이지 210 확장)
- Norman Johnson Uniform Polytopes, 원고(1991)
- N.W. 존슨:균일한 폴리토피와 허니콤의 이론,1966년 토론토 대학교 논문
 rr{p,q,...}.
rr{p,q,...}.


