부르기-두니츠 각

Bürgi–Dunitz angle
Bürgi-Dunitz 및 Flippin-Lodge nucleophile 접근 궤적 각도, B 및 {\ \{FL}, 천체 좌표계의 매개변수 고도 및 방위 유형과 유사했다. 이 천체 좌표계 및 평면 전기영역에 접근하는 핵소자를 기술하는 시스템에서 문제는 평면의 특정 지점에 대해 평면에서 떨어진 점의 위치를 고유하게 기술하는 것이다. 따라서 두 경우 모두 고도형 각도와 방위형 각도의 두 각도를 사용하여 문제를 해결할 수 있다. 참고, 천체 응용의 고도는 표시된 특정 고도와 같이 가장 쉽게 측정되지만, 핵소성인 D 의 고도는 보조각인 Nu-C-O로 가장 쉽게 측정되기 때문에 그 값이 대부분 90° 미만이다(텍스트와 다음 이미지 참조).

부르기-두니츠 각(BD 각도)은 분자의 삼각 불포화 중심에서 핵소체의 "공격"(충돌을 통해 접근)의 기하학을 완전히 정의한 두 각 중 하나인데, 원래 유기 케톤에서 카보닐 중심이지만, 지금은 알데히드, 에스테르, 아미드 카보닐, 알케네스(올레핀)로도 확장된다.[1][2][3]

실질적으로 말하면, Bürgi-Dunitz와 Flippin-Lodge 각도는 치랄 화학 합성에 대한 이해의 발달, 특히 방해를 받는 카보닐 센터에서 핵공격을 하는 동안 비대칭 유도의 현상의 중심이었다(Cram-Felkin– 참조).Anh와 Nguyen 모델).[4][5]

또한, Bürgi-Dunitz 각도의 금지 범위를 채택하는 핵물질의 기초가 되는 스테레오전자 원리는 단백질의[6][7] 일치 안정성에 기여할 수 있으며, 생명의 화학적 기원에 대한 하나의 가설에서 분자의 특정 순응의 안정성을 설명하기 위해 호출된다.[8]

소개

정확히 말하면, 카보닐에서의 핵포함 공격의 경우, Burrgi-Dunitz 각도는 Nu-C-O 결합 각도로 정의되는데, 여기서 Nu는 탄소 원자 C와 결합을 형성하는 핵포함체의 원자를 식별하기 위해 사용된다. 각도는 결정학자 한스 비트 뷔르기와 잭 D의 이름을 따서 명명되었다. 두니츠, 첫 고위 수사관이야

중성 불포화 전기에 대한 핵소재의 접근 동안에 채택된 BD 각도는 주로 불포화 탄소 중심(예: 카보닐 중심)의 분자 궤도(MO) 모양과 수용도에 의존하며, 2차적으로만 핵소피의 분자 궤도상에 의존한다.[1]

핵포함성 "공격"의 기하학을 정의하는 두 각 중 두 번째 각도는 카보닐 탄소나 다른 전기영역 중심부에 부착된 두 대체물 중 하나를 향해 핵포일이 접근하는 "오프셋"을 기술하고 있으며, 기여하는 협력자 Lee A의 이름을 따서 클레이튼 히스콕에 의해 플리핀-로지(FL) 각도로 명명되었다. 플리핀과 에릭 P. 숙박하다.[4]

이러한 각도는 일반적으로 주어진 시스템에 대해 측정 또는 계산된 각도를 의미하는 것으로 해석되며, 원래의 Bürgi-Dunitz 아미노케톤에 대해 역사적으로 관측된 값 범위나 특정 시스템에 대해 계산된 이상화 값(예: 포름알데히드에 대한 하이드라이드 추가, 왼쪽의 이미지)이 아니다. 즉, 하이드라이드 포마이드 시스템의 BD와 FL 각도는 주어진 값 쌍을 생성하는 반면, 다른 시스템에서 관측된 각도는 이 간단한 화학 시스템에 비례하여 달라질 수 있다.[1][3][9]

실험적으로 관찰할 수 있는 것으로서

측정

원래의 Bürgi-Dunitz 측정은 일련의 분자 내 아민-케톤 카보닐 상호작용에 대한 것으로, 메타돈과 프로토핀과 같은 두 가지 기능을 모두 갖는 화합물의 결정이었다. 이는 좁은 범위의 BD 각도 값(105 ± 5°)을 제공했다.; 해당 연산—SCF-LCAO 유형의 분자 궤도 계산—가장 단순한 알데히드인 포름알데히드(HC2=O)의 pi-system에 대한 하이드라이드 음이온(H−)의 s-오르비탈의 접근을 설명하며, BD 각도 값은 107°[2][non-primary source needed]이었다.

따라서, Bürgi, Dunitz 및 그 이후의 많은 다른 사람들은 아미노케톤에 대한 결정학적 측정과 가장 단순한 핵소립 전자파에 대한 계산적 추정치가 이론적 이상인 사면각(사면체 내부각, 109.5°)에 상당히 가깝고 b에 이해되는 기하학과도 매우 일치한다는 점에 주목하였다.e 삼각 중심에서 핵포함성 공격에서 전이 상태를 개발하는 데 중요하다.[citation needed]

  • L-메타돈의 구조는 BD 각도 개념의 개발에서 결정체가 연구된 핵심 분자였다.

  • 알칼로이드인 프로토핀의 구조로, BD 각도 개념의 개발에도 결정체가 연구되었다.

  • 아미네-카르보닐 n→수정* 상호작용은 N··C 거리가 2.555 and이고 부르기-두니츠 각도가 102°인 프로토핀에서 발생한다.[10]

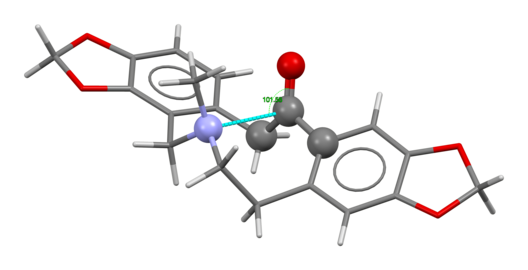
L-메타돈(위, 왼쪽) 구조에서 오른쪽 하단에 투영되는 제3차 아민과 중심부에 있는 카보닐(C=O) 그룹에 유의하여 결정 구조에서 (그들을 연결하는 단일 결합을 중심으로 회전한 후 결정화 과정에서) 분자 내 상호작용을 실시한다.

마찬가지로 프로토핀 구조(위, 중심)에서 분자 중심에 있는 3차 아민, 10mb의 링의 일부 및 링에 있는 그것의 반대편에 있는 C=O 그룹에 주목한다. 이것들은 링 원자의 비틀림 각도의 변화에 의해 허용되는 근육 내 상호작용을 한다.

이론적 설명

포름알데히드에 하이드라이드 첨가
추정 Bürgi-Dunitz(–) ( 각도는 이 간단한 H → HC2=O 핵-필리 첨가물이다.
단순 시스템에서 각의 기초가 되는 HOMO-LUMO 상호작용.
(왼쪽) 알데히드 전기영양체 포름알데히드(R,R'=H)의 불포화삼각 중심에서 하이드라이드 음이온(Nu) 충전된 핵소독성 공격이다. 이 시스템에 대해 최적으로 계산된 값 107°가 표시되며, 대부분의 실험 화학 시스템에서 관측된 둔부 값을 나타낸다.
(오른쪽) 염화물이온(녹색구)과 같은 핵물질의 p형 최고점용 분자궤도(HOMO)와 포름알데히드의 전기생성 카보닐(검은구 탄소, 적구 산소, 백구 수소)의 삼각중심점(LUMO) 중 가장 낮은 점용분자궤도(LUMO)의 접근법 만화. 뷰는 거의 측면에 있으며, 단순성을 위해 카보닐 탄소 원자의 평면 외 왜곡 현상 현상도 생략한다.

HOMO-LUMO 겹침

관측된 BD 각도의 수렴은 핵소포체의 가장 높은 점유 분자 궤도(HOMO)와 전기소포체의 불포화, 삼각 중심에서 가장 낮은 점유 분자 궤도(LUMO) 사이의 중첩을 최대화할 필요성에 기인한다고 볼 수 있다.[1] (비교하여 각 겹침 모델의 관련 무기 화학 개념을 참조한다.)[11][12][13][page needed]

카보닐에 더하는 경우, HOMO는 종종 p형 궤도(예: 아민 질소나 할로이드 음이온에)이며, 일반적으로 LUMO는 케톤 C=O 본드와 그 대체물을 포함하는 평면에 수직인 항균 orbital* 분자 궤도(위 그림 참조)로 이해된다. 핵포함 공격에 대해 관측된 BD 각도는 HOMO와 LUMO 사이에 최적의 중첩을 생성하는 각도에 접근하는 것으로 생각된다(참가 반응제로부터 이와 같이 유사한 에너지의 궤도 및 대칭이 혼합된 후 발생하는 새로운 분자 궤도 에너지를 낮추는 원리에 기초함). 동시에 핵소체는 결합 형성에 불리한 전기영역 그룹의 다른 궤도(포름알데히드에서의 R=R'=H의 단순성 때문에 위 이미지에서는 보이지 않는다)와 중첩되는 것을 피한다.[citation needed]

합병증

정전기 및 반데르 발스 상호작용

실제 화학 반응의 사례를 이해하기 위해, HOMO-LUMO 중심 관점은 위도 BD 각도를 변경하고 방위각 플립핀-로지 각도를 한 대체품 또는 다른 대체품 쪽으로 편향시키는 더 복잡하고 전기적 특유한 정전기 및 Van der Waals 상호작용을 이해함으로써 수정된다(그림 아바보 참조).e).[14][non-primary source needed]

선형 및 회전 역학

BD 각도 이론은 시스템에서 작용하는 역학의 영향(예: 쉽게 변하는 비틀림 각도)이 무시할 수 있는 결정의 "동결" 상호작용에 기초하여 개발되었다. 그러나 일반적인 관심과 사용의 화학의 대부분은 용액에서 굴러떨어지는 분자의 충돌을 통해 일어난다. 따라서 그러한 경우 역학관계가 고려된다.

효소 및 나노물질의 제한된 환경

더욱이 효소와 나노물질 결합 부위와 같은 제한된 반응 환경에서는 무작위 충돌 시 궤도 중복을 가정하는 반응도 개념은 직접 적용할 수 없기 때문에 초기 증거는 반응성을 위한 BD 각도가 상당히 구별될 수 있음을 시사한다.[15][9]

예를 들어 세린 프로테아제(subtilisin)에 의해 아미드의 효소 분열에 대해 결정된 BD 값은 88°로, 하이드라이드-폼알데히드 값 107°와 상당히 구별된다. 또한 89 ± 7°에서 군집화된 서로 다른 단백질 촉매에 의해 매개되는 동일한 반응에 대한 문헌 결정학적 BD 각도 값(즉, 카보닐 탄소 바로 위 또는 아래에서 약간의 오프셋만)의 취합. 동시에, 서브틸리신 FL 값은 8°였고, 조심스러운 컴파일의 FL 각도 값은 4 ± 6°로 군집화되었다(즉, 카보닐 바로 뒤로부터 약간의 오프셋만, 플리핀-로지 각도 기사 참조).[9][non-primary source needed]

참고 항목

참조

  1. ^ a b c d 플레밍, I. (2010) 분자 궤도 및 유기 화학 반응: 참조판, 존 와일리 & 선즈, 페이지 214–215.
  2. ^ a b Bürgi, H.-B.; Dunitz, J. D.; Lehn. J.-M.; Wipff, G. (1974). "Stereochemistry of reaction paths at carbonyl centres". Tetrahedron. 30 (12): 1563–1572. doi:10.1016/S0040-4020(01)90678-7.
  3. ^ a b Cieplak, A.S. (2008) 유기 첨가 및 제거 반응: 구조상 상관관계에서의 카보닐 유도체의 변환 경로, Vol. 1 (H.-B) 부르기 & J. D. 뒤니츠, 에드스), 뉴욕:존 와일리 & 선즈, 페이지 205–302, esp. 216-218. [doi:10.1002/9783527616091.ch06; ISBN 9783527616091 ]
  4. ^ a b 히스콕, C.H. (1990) 탄소-탄소 결합형성 반응에서 이질소성 선택성의 이해와 제어, 알드리히치미카 액타 23(4):94-111, esp. 페이지 101, [1] 참조, 2014년 6월 9일에 접속했다.
  5. ^ 가울리, R.E. & Aube, J. 1996, 비대칭 합성 원리 (Tetrahedron Organic Chemical Series, Vo. 14), 페이지 121-130, esp. 127f.
  6. ^ Bartlett, G.J.; Choudhary, A.; Raines, R.T.; Woolfson, D.N. (2010). "n→π* interactions in proteins". Nat. Chem. Biol. 6 (8): 615–620. doi:10.1038/nchembio.406. PMC 2921280. PMID 20622857.
  7. ^ Fufezan, C. (2010). "The role of Buergi‐Dunitz interactions in the structural stability of proteins". Proteins. 78 (13): 2831–2838. doi:10.1002/prot.22800. PMID 20635415. S2CID 41838636.
  8. ^ Choudhary, A.; Kamer, K.J.; Powner, M.W.; Sutherland, J.D.; Raines, R.T. (2010). "A stereoelectronic effect in prebiotic nucleotide synthesis". ACS Chem. Biol. 5 (7): 655–657. doi:10.1021/cb100093g. PMC 2912435. PMID 20499895.
  9. ^ a b c Radisky, E.S. & Koshland, D.E.(2002) 프로테아제 억제제를 위한 막힌 거터 메커니즘, Proc. 나틀. 아카드. Sci. U.S.A., 99(16):10316-10321, 2014년 11월 28일 접속 [2] 참조.
  10. ^ Hall, S. R.; Ahmed, F. R. (1968). "The crystal structure of protopine, C20H19O5N". Acta Crystallogr. B. 24 (3): 337–346. doi:10.1107/S0567740868002347.
  11. ^ Hoggard, P.E. (2004) 각도 오버랩 모델 파라미터, Structure. 본드 106, 37
  12. ^ 버들, J.K. (1978) 전이 금속 복합체의 구조와 결합에 대한 새로운 시각, Adv. 이너그, 화학 21, 113
  13. ^ Purcell, K.F. & Kotz, J.C. (1979) 무기 화학, 필라델피아, PA:Sunders 컴퍼니.[page needed]
  14. ^ Lodge, E.P. & Heathcock, C.H. (1987) Steric effects와 시그마*-오르비탈 에너지는 치랄 알데히드, J. Am.에 더하여 분뇨제거에 중요하다. 화학, 109:3353-3361
  15. ^ 예를 들어 Light, S.H.; Minasov, G.; Duban, M.E. & Anderson, W.F. (2014) Bürgi-Dunitz 입체화학 원리를 준수하려면 Schiff-base 형성에 상당한 구조적 재배열이 필요하다. 트랜스알돌라아제 콤플렉스의 통찰력, 액타 크리스탈로그르. D 70(Pt 2):544-52, DOI: 10.1107/S1399004713030666, [3] 참조, 2014년 6월 10일 액세스.