편미분 방정식
Burgers 방정식 또는 Bateman-Burgers 방정식 은 유체역학 ,[2] 비선형 음향학 ,[3] 기체 역학 및 교통 흐름 과 같은 응용 수학 의 다양한 영역에서 발생하는 기본 편미분 방정식 및 대류-확산 방정식 입니다[1] [4] 이 방정식은 1915년[5] [6] 해리 베이트먼 에 의해 처음 소개되었고 이후 1948년 요하네스 마르티누스 버거 에 의해 연구되었습니다.[7]
주어진 필드 ( x , {\displaystyle u(x, t)} 확산 계수 (또는 원래 유체 역학적 맥락에서와 같은 운동학적 점도 ) {\displaystyle u }, 점성 버거 방정식이라고 도 함)은 소산 시스템 입니다.
∂ u ∂ t + u ∂ u ∂ x = ν ∂ 2 u ∂ x 2 . {\displaystyle {\frac {\partial u}{\partial t}+u{\frac {\partial u}{\partial x}=\n u {\frac {\partial ^{2}u}{\partial x^{2}}} 확산항이 없는 경우(즉, ν = 0 {\displaystyle u =0}), 비점성 Burgers' 방정식 이 됩니다.
∂ u ∂ t + u ∂ u ∂ x = 0 , {\displaystyle {\frac {\partial u}{\partial t}+u{\frac {\partial u}{\partial x}=0,} 불연속성(충격파 )을 발전시킬 수 있는 보존 방정식 의 원형입니다.
보수적 인 형태에서 버거 방정식은
∂ u ∂ t + 1 2 ∂ u 2 ∂ x = ν ∂ 2 u ∂ x 2 . {\displaystyle {\frac {\partial u}{\partial t}+{\frac {1}{2}}{\frac {partial u^{2}}{\partial x}=\n u {\frac {\partial ^{2}u}{\partial x^{2}}}
인비스시드 버거 방정식 충격이 형성될 때까지 두 공간 변수에서 비점성 버거 방정식을 수치 시뮬레이션한 것입니다. 비점성 버거 방정식은 보존 방정식 으로, 일반적으로 1차 준선형 쌍곡선 방정식 입니다. 방정식과 초기 조건에 대한 해
∂ u ∂ t + u ∂ u ∂ x = 0 , u ( x , 0 ) = f ( x ) {\displaystyle {\frac {\partial u}{\partial t}+u{\frac {\partial u}{\partial x}=0,\quad u(x,0)=f(x)} 특성의 방법 으로 구성할 수 있습니다. 특성 방정식은 d x d t = u , d u d t = 0. {\displaystyle {\frac {dx}{dt}=u,\quad {\frac {du}{dt}}=0.}
두 번째 방정식의 적분은 u {\displaystyle }
u = c , x = u t + ξ {\displaystyle u=c,\quad x=ut+\xi} 여기서 {\displaystyle 평면 의 x축 (t = 0)에 있는 점(또는 매개 변수)입니다. Since u {\displaystyle u} x {\displaystyle x} u {\displaystyle u} x = ξ {\displaystyle x=\xi } u = c = f ( ξ ) {\displaystyle u=c=f(\xi )} 따라서 {\displaystyle x = f ( ξ ) t + ξ . {\displaystyle x=f(\xi)t+\xi .}
따라서 해결책은 다음과 같습니다.
u ( x , t ) = f ( ξ ) = f ( x − u t ) , ξ = x − f ( ξ ) t . {\displaystyle u(x,t)=f(\xi )=f(x-ut),\quad \xi =x-f(\xi )t.} 이는 특성이 교차하지 않는 경우 비점성 버거 방정식의 해를 결정하는 암묵적인 관계입니다. 특성이 교차하면 PDE에 대한 고전적인 해결책이 존재하지 않고 충격파 가 형성됩니다. 특성이 교차할 수 있는지 여부는 초기 조건에 따라 달라집니다. 사실, 충격파가 형성되기 전의 파괴 시간 은 다음과[8] [9] t b = − 1 인폼의 x ( f ′ ( x ) ) {\displaystyle t_{b}={\frac {-1}{\inf _{x}\left(f^{\prime}(x))\right }}}
선형 초기조건에 대한 Inviscid Burgers 방정식 수브라흐마니안 찬드라세카르 (Subrahmanyan Chandrasekhar)는 1943년에 초기 조건이 선형, 즉 f( x ) = x {\displaystyle f(x = ax+b} , 명시적인 해결책은
u ( x , t ) = a x + b a t + 1 . {\displaystyle u(x,t)={\frac {ax+b}{at+1}}.} 이 해는 방정식에 나타나는 독립 변수의 수만큼 임의의 상수를 포함하기 때문에 비점성 버거 방정식의 완전 [11] [better source needed 이 완전 적분을 사용하여 찬드라세카르는 완전 적분의 외피
점성 버거 방정식 이는 초기 가우시안 프로파일을 사용하여 점성 2차원 버거 방정식의 수치 해입니다. 우리는 충격이 형성되고 이동하면서 점성으로 인한 충격의 소멸을 봅니다. 점성 버거 방정식은 콜-호프 변환 에 의해 선형 방정식으로 변환될 수 있습니다.[12] [13] [14]
u ( x , t ) = − 2 ν ∂ ∂ x ln의 φ ( x , t ) , {\displaystyle u(x,t)=-2\n u {\frac {\partial }{\partial x}\ln \varphi(x,t),} 그것을 방정식으로 바꾸는 겁니다.
2 ν ∂ ∂ x [ 1 φ ( ∂ φ ∂ t − ν ∂ 2 φ ∂ x 2 ) ] = 0 , {\display style 2\n u {\frac {\partial }{\partial x}\left [{\frac {1}{\varphi }\left ({\frac {\partial \varphi }{\partial t}-\n u {\frac {\partial ^{2}\varphi}{\partial x^{2}}\right)=0,} 다음을 얻기 위해x {\displaystyle x}
∂ φ ∂ t − ν ∂ 2 φ ∂ x 2 = φ d f ( t ) d t , {\displaystyle {\frac {\partial \varphi }{\partial t}-\n u {\frac {\partial ^{2}\varphi}{\partial x^{2}}=\varphi {\frac {df(t)}{dt}},} 여기서 df dt {\displaystyle df/dt} 변환 φ → displaystyle \varphi \to }}( 함수 {\displaystyle 영향 방정식 의 것 으로 줄어듭니다.
∂ φ ∂ t = ν ∂ 2 φ ∂ x 2 . {\displaystyle {\frac {\partial \varphi }{\partial t}=\n u {\frac {\partial ^{2}\varphi }{\partial x^{2}}.} 확산 방정식을 풀 수 있습니다 . 즉, {\displaystyle \
φ ( x , t ) = 1 4 π ν t ∫ − ∞ ∞ φ 0 ( x ′ ) exp [ − ( x − x ′ ) 2 4 ν t ] d x ′ . {\displaystyle \varphi(x,t)={\frac {1}{\sqrt {4\pi\n u t}}}\int _{-\infty }^{\infty }\varphi _{0}(x')\exp \left[-{\frac {(x-x')^{2}}{4\n u}}\right]dx'} 초기 함수 ( {\displaystyle varphi _ 함수 ( (x {\displaystyle 0
ln의 φ 0 ( x ) = − 1 2 ν ∫ 0 x f ( x ′ ) d x ′ , {\displaystyle \ln \varphi _{0}(x)=-{\frac {1}{2\n u }}\int _{0}^{x}f(x')dx',} 하한선이 임의로 선택된 경우. 콜-호프 변환을 뒤집으면 우리는
u ( x , t ) = − 2 ν ∂ ∂ x ln의 { 1 4 π ν t ∫ − ∞ ∞ exp [ − ( x − x ′ ) 2 4 ν t − 1 2 ν ∫ 0 x ′ f ( x ″ ) d x ″ ] d x ′ } {\displaystyle u(x,t)=-2\n u {\frac {\partial }{\partial x}\ln \left\{\frac {1}{\sqrt {4\pi\n u t}}}\int _{-\infty }^{\infty }\exp \left[-{\frac {(x-x')^{2}}{4\n u t}}-{\frac {1}{2\n u }}\int _{0}^{x'}f(x'')dx''\right]dx'\right\}} 로그 함수의 인수에서 시간에 의존하는 선행 인자를 제거함으로써 다음과 같이 단순화합니다.
u ( x , t ) = − 2 ν ∂ ∂ x ln의 { ∫ − ∞ ∞ exp [ − ( x − x ′ ) 2 4 ν t − 1 2 ν ∫ 0 x ′ f ( x ″ ) d x ″ ] d x ′ } . {\displaystyle u(x,t)=-2\n u {\frac {\partial }{\partial x}\ln \left\{\int _{-\infty}^{\infty }\exp \[-{\frac {(x-x')^{2}}{4\n u t}}-{\frac {1}{2\n u }}\int _{0}^{x'}f(x'')dx''\right]dx'\right\}.} 점성 버거 방정식의 몇 가지 명시적 해 점성 버거 방정식에 대한 명시적인 표현을 사용할 수 있습니다. 물리적으로 관련된 솔루션 중 일부는 다음과 같습니다.[16]
꾸준히 전파되는 이동파 If u ( x , 0 ) = f ( x ) {\displaystyle u(x,0)=f(x)} f ( − ∞ ) = f − {\displaystyle f(-\infty )=f^{-}} f ( + ∞ ) = f + {\displaystyle f(+\infty )=f^{+}} f ′ ( x ) < 0 {\displaystyle f'(x)<0} 다음으로 주어진 진행파 솔루션(일정 속도 ( f f {\displaystyle f^{+} f^{-}/2}) .
u ( x , t ) = c − f + − f − 2 탠 [ f + − f − 4 ν ( x − c t ) ] . {\displaystyle u(x,t)=c-{\frac {f^{+}-f^{-}}{2}}\tanh \left[{\frac {f^{+}-f^{-}}{4\n u }}(x-ct)\right].} 이 솔루션은 약한 충격파 에[15] f {\displaystyle 2} f 0 {\displaystyle 0}
u ( x , t ) = 2 1 + e x − t {\displaystyle u(x,t)={\frac {2}{1+e^{x-t}}}} c 1 {\displaystyle 1}
델타는 초기 조건으로 기능합니다. 만약 ( x , 0 ) 2 Re ) {\displaystyle x u Re\delta (x Re {\displaystyle Re}( 레이놀즈 수 )는 상수이고, 다음은[17]
u ( x , t ) = ν π t [ ( e R e − 1 ) e − x 2 / 4 ν t 1 + ( e R e − 1 ) e r f c ( x / 4 ν t ) / 2 ] . {\displaystyle u(x,t)= {\sqrt {\frac {\n u }{\pi t}}}\left[{\frac {(e^{Re}-1)e^{-x^{2}/4\n u t}}{1+(e^{Re}-1)\mathrm {erfc} (x/{\sqrt {4\n u t}})/{\sqrt {2}}}}\right].} 제한 Re 0 {\displaystyle Re\to }
u ( x , t ) = 2 ν R e 4 π ν t exp ( − x 2 4 ν t ) . {\displaystyle u(x,t)= {\frac {2\n u Re}{\sqrt {4\pi \n u t}}}\exp \left(-{\frac {x^{2}}{4\n ut}}\right)} 반면, Re displaystyle to
u ( x , t ) = { x t , 0 < x < 2 ν R e t , 0 , 그렇지않으면 . {\displaystyle u(x,t)={\begin {case}{\frac {x}{t}},\quad 0<x<{\sqrt {2\n uRe\,t},\0,\quad {\text{그렇지 않으면}}. \end{case}} 충격파 Ret displaystyle x {\sqrt uRe\,t}} ν /t {\displaystyle sqrt uRe/t}}.}
N파해 N-wave 솔루션은 압축파에 이어 라팩션파로 구성됩니다. 이 유형의 솔루션은 다음과 같습니다.
u ( x , t ) = x t [ 1 + 1 e R e 0 − 1 t t 0 exp ( − R e ( t ) x 2 4 ν R e 0 t ) ] − 1 {\displaystyle u(x,t)={\frac {x}{t}}\left[1+{\frac {1}{e^{Re_{0}-1}}}{\sqrt {\frac {t}{t_{0}}}}\exp \left(-{\frac {Re(t)x^{2}}{4\n u Re_{0}t}}\right)\right]^{-1}} 여기서 R {\displaystyle R_{0}} t 0 {\displaystyle t_{0}} Re ( t ) 1 u x (1 t u )τ = t 0인 int _{0}^{\infty }udx= ln(1+{\sqrt tau/ {\displaystyle \tau = 0}{\sqrt {e^{Re_{0}- }} varying
기타양식 일반화 버거 방정식 일반화된 버거 방정식은 준선형 대류를 보다 일반화된 형태로 확장합니다.
∂ u ∂ t + c ( u ) ∂ u ∂ x = ν ∂ 2 u ∂ x 2 . {\displaystyle {\frac {\partial u}{\partial t}+c(u){\frac {\partial u}{\partial x}=\n u {\frac {\partial ^{2}u}{\partial x^{2}}} 여기서 c( u ) {\displaystyle (u)} inviscid ν = 0 {\displaystyle u =0} 여전히 u ) {\displaystyle c(u) } 특성 방법 을 사용하여 그 해를 구성할 수 있습니다.
확률적 버거 방정식 시공간 잡음 ( {\displaystyle {\ W , 여기서 W displaystyle W } {\displaystyle L^{ mathbb {R })} Wiener 프로세스는 확률적 버거 방정식을 형성합니다.
∂ u ∂ t + u ∂ u ∂ x = ν ∂ 2 u ∂ x 2 − λ ∂ η ∂ x . {\displaystyle {\frac {\partial u}{\partial t}+u{\frac {\partial u}{\partial x}=\n u {\frac {\partial ^{2}u}{\partial x^{2}}-\lambda {\frac {\partial \eta}{\partial x}}}
이 확률적 PDE 는 u x , ) h display h(x, t ) 필드 카다르–파리시–장 방정식 의 1차원 버전입니다.
참고 항목 참고문헌 ^ Misra, Souren; Raghurama Rao, S. V.; Bobba, Manoj Kumar (2010-09-01). "Relaxation system based sub-grid scale modelling for large eddy simulation of Burgers' equation" . International Journal of Computational Fluid Dynamics . 24 (8): 303–315. Bibcode :2010IJCFD..24..303M . doi :10.1080/10618562.2010.523518 . ISSN 1061-8562 . S2CID 123001189 . ^ 그것은 Navier와 관련이 있습니다. – 압력 항이 제거된 스톡스 운동량 방정식 : 여기서 변수는 유속 y =u 입니다. ^ 이는 엄격하게 전방으로 전파하는 파동을 가정하고 지연된 시간 프레임에 대한 좌표 변환을 사용하는 Westerbelt 방정식 에서 발생합니다. 여기서 변수는 압력 입니다. ^ Musha, Toshimitsu; Higuchi, Hideyo (1978-05-01). "Traffic Current Fluctuation and the Burgers Equation" . Japanese Journal of Applied Physics . 17 (5): 811. Bibcode :1978JaJAP..17..811M . doi :10.1143/JJAP.17.811 . ISSN 1347-4065 . S2CID 121252757 . ^ Bateman, H. (1915). "Some recent researches on the motion of fluids" . Monthly Weather Review . 43 (4): 163–170. Bibcode :1915MWRv...43..163B . doi :10.1175/1520-0493(1915)43<163:SRROTM>2.0.CO;2 ^ 위담, G. B. (2011). 선형 및 비선형 파동(Vol. 42). 존 와일리 & 선즈. ^ Burgers, J. M. (1948). "A Mathematical Model Illustrating the Theory of Turbulence". Advances in Applied Mechanics . 1 : 171–199. doi :10.1016/S0065-2156(08)70100-5 . ISBN 9780123745798 ^ Olver, Peter J. (2013). Introduction to Partial Differential Equations doi :10.1007/978-3-319-02099-0 . ISBN 978-3-319-02098-3 S2CID 220617008 . ^ Cameron, Maria (February 29, 2024). "Notes on Burger's Equation" (PDF) . University of Maryland Mathematics Department, Maria Cameron's personal website . Retrieved February 29, 2024 . ^ Chandrasekhar, S. (1943). On the decay of plane shock waves (Report). Ballistic Research Laboratories. Report No. 423. ^ Forsyth, A. R. (1903). A Treatise on Differential Equations . London: Macmillan.^ Cole, Julian (1951). "On a quasi-linear parabolic equation occurring in aerodynamics" . Quarterly of Applied Mathematics . 9 (3): 225–236. doi :10.1090/qam/42889 JSTOR 43633894 .^ Eberhard Hopf (September 1950). "The partial differential equation ut + uux = μuxx ". Communications on Pure and Applied Mathematics . 3 (3): 201–230. doi :10.1002/cpa.3160030302 .^ Kevorkian, J. (1990). Partial Differential Equations: Analytical Solution Techniques . Belmont: Wadsworth. pp. 31–35. ISBN 0-534-12216-7 ^ a b Landau, L.D., & Lifshitz, E.M. (2013). 유체역학: 란다우와 리프쉬츠: 이론물리학 과정, 제6권(제6권). 엘스비어. Page 352-354. ^ 살리, A. "버거 방정식" 인도 우주 과학 기술 연구소, Thiruvanananthapuram (2016). ^ 휘담, 제럴드 베레스포드. 선형 및 비선형 파동. 존 와일리 & 선즈, 2011. ^ Courant, R. & Hilbert, D. 수학 물리학의 방법. 제2권 ^ Wang, W.; Roberts, A. J. (2015). "Diffusion Approximation for Self-similarity of Stochastic Advection in Burgers' Equation". Communications in Mathematical Physics . 333 (3): 1287–1316. arXiv :1203.0463 Bibcode :2015CMaPh.333.1287W . doi :10.1007/s00220-014-2117-7 . S2CID 119650369 .
외부 링크 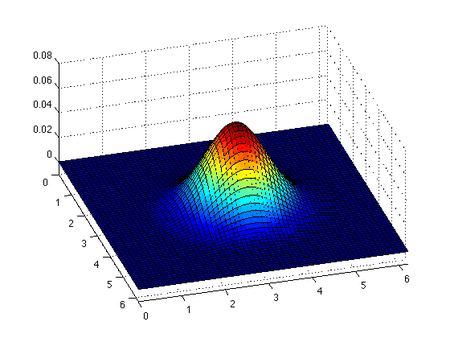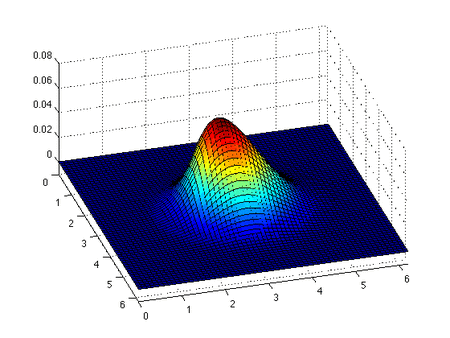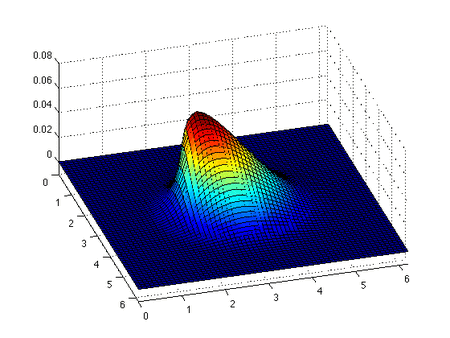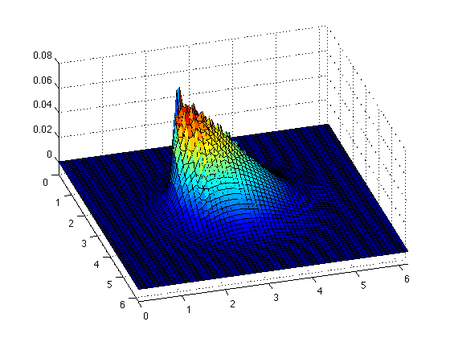

















![{\displaystyle 2\nu {\frac {\partial }{\partial x}}\left[{\frac {1}{\varphi }}\left({\frac {\partial \varphi }{\partial t}}-\nu {\frac {\partial ^{2}\varphi }{\partial x^{2}}}\right)\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97af41d8883f61833913ebf402c8725dfdcdf0e5)

 임의의 시간 함수입니다. 변환 φ →
임의의 시간 함수입니다. 변환 φ →
![{\displaystyle \varphi (x,t)={\frac {1}{\sqrt {4\pi \nu t}}}\int _{-\infty }^{\infty }\varphi _{0}(x')\exp \left[-{\frac {(x-x')^{2}}{4\nu t}}\right]dx'.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82230ee066766dfdb4bff27c8347f3a83964b755)

![{\displaystyle u(x,t)=-2\nu {\frac {\partial }{\partial x}}\ln \left\{{\frac {1}{\sqrt {4\pi \nu t}}}\int _{-\infty }^{\infty }\exp \left[-{\frac {(x-x')^{2}}{4\nu t}}-{\frac {1}{2\nu }}\int _{0}^{x'}f(x'')dx''\right]dx'\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f16e08665539a637c6328a784ccc7732b5d83a0)
![{\displaystyle u(x,t)=-2\nu {\frac {\partial }{\partial x}}\ln \left\{\int _{-\infty }^{\infty }\exp \left[-{\frac {(x-x')^{2}}{4\nu t}}-{\frac {1}{2\nu }}\int _{0}^{x'}f(x'')dx''\right]dx'\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58353e8ed8bb40ca08552efc21b08231d15ee786)




![{\displaystyle u(x,t)=c-{\frac {f^{+}-f^{-}}{2}}\tanh \left[{\frac {f^{+}-f^{-}}{4\nu }}(x-ct)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43913902ecb0b3986963f3627aa2f0be142cbe3d)



![{\displaystyle u(x,t)={\sqrt {\frac {\nu }{\pi t}}}\left[{\frac {(e^{Re}-1)e^{-x^{2}/4\nu t}}{1+(e^{Re}-1)\mathrm {erfc} (x/{\sqrt {4\nu t}})/{\sqrt {2}}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e5c9d50559a05fcecbacfefbdb02c938e0f01ec)


![{\displaystyle u(x,t)={\frac {x}{t}}\left[1+{\frac {1}{e^{Re_{0}-1}}}{\sqrt {\frac {t}{t_{0}}}}\exp \left(-{\frac {Re(t)x^{2}}{4\nu Re_{0}t}}\right)\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c64c2b7babb8c59493f57ca96f1f620a23bc72a2)

 u의 임의의 함수입니다. inviscid ν = 0
u의 임의의 함수입니다. inviscid ν = 0


