뱅크 턴

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '은행 턴'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2009년 2월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

뱅크 턴(banked turn)은 차량이 뱅킹하거나 기울어지는 방향의 턴 또는 변경으로, 일반적으로 턴의 안쪽을 향합니다.도로나 철도의 경우, 이는 일반적으로 노반이 곡선 안쪽을 향해 횡방향으로 내리막길을 가지고 있기 때문입니다.뱅크 각도는 차량이 수평에 대해 세로 축을 중심으로 기울어진 각도입니다.

평탄한 표면에서

뱅크 각도가 0일 경우 표면은 평평하고 법선력은 수직으로 위쪽으로 향합니다.차량이 경로를 따라 회전하는 유일한 힘은 마찰 또는 트랙션입니다.이것은 차가 반지름 r의 원을 그리며 주행한다고 가정할 때 부등식으로 표현될 수 있는 관계인 구심력을 제공할 수 있을 만큼 커야 한다.

${\displaystyle \mu mg>{mv^{2} \over r}.}$

우측의 표현은 구심 가속도에 질량을 곱한 값이며, 이는 차량을 회전시키는 데 필요한 힘입니다.왼쪽은 최대 마찰력으로 마찰계수 μ에 정규력을 곱한 값과 같습니다.최대 코너링 속도 재배열은 다음과 같습니다.

$(\displaystyle v<\displayrt {r\mu g})}$

μ는 정적 마찰 또는 동적 마찰 계수가 될 수 있습니다.후자의 경우 차량이 커브 주위로 미끄러지면 마찰이 한계에 도달하고 부등식이 방정식이 됩니다.이는 또한 다운포스와 같은 효과를 무시하여 정상력과 코너링 속도를 높일 수 있습니다.

무마찰 뱅크 턴

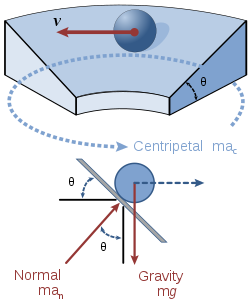
차량이 평평한 원을 따라 주행하는 것과 달리, 경사 모서리는 차량이 이동 경로를 유지하도록 하는 추가 힘을 가하고 차량이 원형으로 "끌리거나" 밀려나는 것을 방지합니다(또는 레일 휠이 휠 플랜지에 거의 닿을 정도로 옆으로 움직이는 것을 방지합니다).이 힘은 차량의 정상 힘의 수평 구성 요소입니다.마찰이 없는 경우, 원의 중심 방향으로 차량에 작용하는 유일한 힘은 정상 힘입니다.따라서, 뉴턴의 제2법칙에 따라, 우리는 정규력의 수평 성분을 구심 ^[1]가속도를 곱한 질량과 동일하게 설정할 수 있다.

${{displaystyle N\sin \theta = {mv^{2} \over r}}$

수직방향으로 움직임이 없기 때문에 시스템에 작용하는 모든 수직력의 합계는 0이어야 합니다.따라서 차량 정상력의 수직 구성 요소를 ^[1]중량과 동일하게 설정할 수 있습니다.

$\displaystyle N\cos \theta =mg$

위의 정규력에 대한 방정식을 풀고 이 값을 이전 방정식에 대입하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle {mv^2} \over r}={mg\tan \theta }}$

이는 다음과 같습니다.

${\displaystyle {v^2} \over r}={g\tan \theta }}$

속도 문제 해결 방법:

${\displaystyle v=syslogrt {rg\tan \theta }}$

이는 마찰이 없는 상태에서 주어진 경사각과 곡률 반지름으로 차량이 지정된 경로를 유지할 수 있는 속도를 제공합니다.이 속도의 크기는 선회 또는 ^[2]곡선의 "정격 속도" (또는 철도의 경우 "균형 속도")라고도 합니다.곡선의 정격 속도는 모든 무거운 물체에 대해 동일하며 기울지 않은 곡선의 정격 속도는 0입니다.

마찰이 있는 뱅크 턴

마찰력이 시스템에 미치는 영향을 고려할 때 마찰력이 어느 쪽을 가리키는지 다시 한 번 확인해야 합니다.우리 자동차의 최고 속도를 계산할 때 마찰력은 경사를 아래로 향하고 원의 중심을 향하게 됩니다.그러므로 우리는 마찰의 수평 성분을 정상 힘의 수평 성분과 더해야 합니다.이 두 힘의 합계는 회전 중심 방향의 새로운 순력(구심력)입니다.

${\displaystyle {mv^{2} \over r}=\mu _{s}N\cos \theta +N\sin \theta }$

다시 한 번 말하지만, 수직 방향에서는 움직임이 없기 때문에 서로 마주보는 모든 수직력을 동일하게 설정할 수 있습니다.이러한 힘에는 위를 향한 정상 힘의 수직 구성 요소, 그리고 자동차의 무게와 아래를 향한 마찰력의 수직 구성 요소가 포함됩니다.

${\displaystyle N\cos \theta =\mu _{s}N\sin \theta +mg}$

위의 질량 방정식을 풀고 이 값을 이전 방정식에 대입하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle {v^2}\left(N\cos \theta -\mu _{s}N\sin \theta \오른쪽)\over rg}=\mu _{s}N\cos \theta +N\sin \theta }$

v에 대한 해결 방법:

$(\displaystyle v=mu {rg\left(\sin \theta +\mu _{s}\cos \theta \right) \over \cos \theta -\mu _{s}\sin \theta })=mu {rt {rft(\tan \thetft(\tan \thetft) \mu _{s} \tan} \ta } \tan\ta } } } } } } over 1\ta }$

이 방정식은 주어진 경사각, 정적 마찰계수 및 곡률반경을 가진 자동차의 최대 속도를 제공합니다.최소 속도에 대한 유사한 분석을 통해 다음과 같은 방정식이 제시된다.

$(\displaystyle v=sigrt {rg\left(\sin \theta -\mu _{s}\cos \theta \right) \over \cos \theta +\mu _{s}\sin \theta })=sigrt {rt {rt(\t(\tan \thetft)\ta -\mu _{s} \tan} \ta } \ta } } } \tan\tan\ta } } } } } }$

후자 분석의 차이는 자동차의 최소 속도(원 바깥쪽 방향)에 대한 마찰 방향을 고려할 때 나타난다.이것에 의해 구심방향 및 수직방향의 힘 방정식에 마찰을 삽입할 때 역연산을 할 수 있다.

도로 커브가 부적절하게 둑을 오르면 도로 이탈 및 정면 충돌 위험이 높아집니다.편경사가 2% 부족하면(예를 들어, 6%가 되어야 하는 곡선에서 4% 편경사) 충돌 빈도가 6% 증가하고 5% 부족하면 15% 증가할 ^[3]것으로 예상할 수 있습니다.지금까지 고속도로 엔지니어는 부적절하게 둑을 이룬 곡선을 식별하고 관련 완화 조치를 설계할 수 있는 효율적인 도구가 없었습니다.최신 프로파일로그래프는 도로 곡률 및 교차 경사(경사 각도) 데이터를 모두 제공할 수 있습니다.부적절하게 뱅크된 턴을 평가하는 방법에 대한 실질적인 시연은 EU Roadex III 프로젝트에서 개발되었습니다.아래 링크된 참조 문서를 참조하십시오.

항공학의 뱅크 턴

고정익 항공기가 선회할 때(방향을 변경할 때) 항공기는 날개를 원하는 선회 방향으로 기울일 수 있도록 뱅크 위치로 굴러가야 한다.회전이 완료되면 항공기는 직선 ^[4]비행을 재개하기 위해 날개 높이로 다시 회전해야 한다.

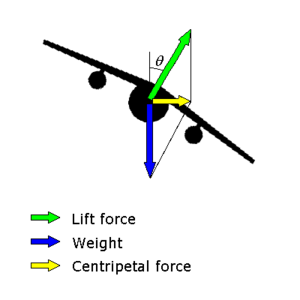
움직이는 차량이 회전할 때 차량에 작용하는 힘은 구심 가속을 유발하기 위해 순 내향력에 더해야 합니다.항공기가 선회하는 경우, 구심 가속을 일으키는 힘은 항공기에 작용하는 리프트의 수평 구성요소이다.

직선 수평 비행에서 항공기에 작용하는 리프트는 수직 위쪽으로 작용하여 아래로 작용하는 항공기의 무게를 상쇄한다.항공기가 수평 비행(즉, 일정한 고도에서)을 계속하기 위해서는 수직 구성요소가 항공기의 무게와 동일한 상태로 유지되어야 하며, 따라서 조종사는 스틱을 뒤로 당겨 엘리베이터를 적용하여 기수를 위로 올리고, 따라서 공격 각도를 증가시켜 날개 리프트를 증가시켜야 한다.총(현재 각진) 리프트는 항공기 중량보다 크다. 초과 리프트는 총 리프트의 수평 구성요소이며, 이는 항공기가 안쪽으로 가속하고 회전을 실행하는 순 힘이다.

구심 가속도는 다음과 같습니다.

${\displaystyle a={v^{2} \over r}}$

뱅크 각도가 θ인 균형 회전 시에는 리프트가 수직에서 away 떨어진 각도로 작용한다.리프트를 수직 구성 요소와 수평 구성 요소로 분해하는 데 유용합니다.

뉴턴의 수평방향 제2법칙은 수학적으로 다음과 같이 표현될 수 있다.

${{displaystyle L\sin \theta = {mv^{2} \over r}}$

여기서:

L은 항공기에 작용하는 리프트이다.

θ는 항공기의 뱅크 각도이다.

m은 항공기의 질량이다.

v는 항공기의 실제 비행 속도입니다.

r은 회전 반지름입니다.

직선 비행에서 양력은 항공기 무게와 같다.회전 비행 시 리프트는 항공기 중량을 초과하며, 항공기 중량(mg)을 뱅크 각도의 코사인(cosine)으로 나눈 값과 같다.

${\displaystyle L={mg\over\cos\theta}}$

여기서 g는 중력장 강도입니다.

이제 회전 반경을 ^[5]계산할 수 있습니다.

${\displaystyle r={v^{2} \over {g\tan \theta }}}$

이 공식은 회전반경이 항공기의 실제 비행속도의 제곱에 비례한다는 것을 보여준다.대기속도가 높을수록 회전반경이 커지고 대기속도가 낮을수록 반지름이 작아집니다.

이 공식은 또한 뱅크의 각도에 따라 회전반경이 감소함을 보여준다.뱅크의 각도가 높을수록 회전 반경이 작아지고 뱅크의 각도가 낮을수록 반지름이 커집니다.

일정한 고도에서의 뱅크 회전에서는 부하 계수는 1/cosθ가 됩니다.직선 및 수평 비행의 하중 계수는 1임을 알 수 있다. 왜냐하면 cos(0) = 1이기 때문에 그리고 일정한 고도를 유지하기에 충분한 양력을 생성하기 위해서는 뱅크 각도가 90°에 근접하고 cos θ가 0에 근접함에 따라 하중 계수는 무한대에 도달해야 한다.항공기의 구조적 한계나 탑승자의 물리적 내구성이 그 전에 훨씬 초과되기 때문에 물리적으로 불가능하다.

육상 경기에서의 뱅크 턴

대부분의 실내 육상 경기장은 트랙이 실외 트랙보다 작기 때문에 뱅크 턴이 있습니다.이러한 작은 트랙의 타이트한 턴은 보통 선수들이 커브를 돌 때 안쪽으로 기울고 원심력을 중화시킬 수 있도록 한다. 린은 특히 스프린트 이벤트에서 두드러진다.^[6]

• 

  둑이 있는 실내 트랙에서 턴을 하는 스프린터

「 」를 참조해 주세요.

레퍼런스

추가 정보

수상 차량

• 서웨이, 레이먼드과학자와 엔지니어를 위한 물리학.Cengage Learning, 2010.
• 건강과 안전 문제, EU의 Roadex III 프로젝트는 제대로 정비되지 않은 도로망에 의해 제기되는 건강과 안전 문제에 관한 것이다.

항공학

• Kermode, A.C.(1972) 비행 메커니즘, 제8장, 제10판, Longman Group Limited, 런던 ISBN 0-582-23740-8
• Clancy, L.J.(1975), 공기역학, Pitman Publishing Limited, London ISBN 0-273-01120-0
• Hut, H.H. Jr.(1960), 해군 항공기를 위한 공기역학, 플로리다 주, 전국 비행장, 리프린트

외부 링크

수상 차량

• http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/carbank.gif
• https://web.archive.org/web/20051222173550/http://whitts.alioth.net/
• http://www.batesville.k12.in.us/physics/PHYNET/Mechanics/Circular%20Motion/banked_no_friction.htm

항공학

• NASA: 뱅킹 턴 가이드라인
• aerospaceweb.org: 뱅크 각도 및 G(수학)
• 조종사 항공 지식 안내서