사분위의 이탄젠트

대수 평면 곡선의 이론에서 일반 사분면 곡선은 두 곳에서 곡선과 접하는 선인 28개의 비탄젠트 선을 가진다.이 선들은 복잡한 투영 평면에 존재하지만, 이 선들 중 28개 모두 실제 숫자를 좌표로 가지고 있어 유클리드 평면에 속하는 사분위 곡선을 정의할 수 있다.

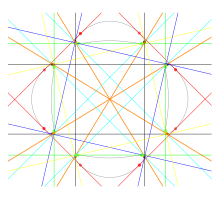
28개의 실제 비텐젠트를 가진 명시적 사분위는 플뤼커(1839)^[1]가 처음으로 부여한 것으로 플뤼커는 보여주었듯이 모든 사분위의 실제 비텐젠트의 수는 28, 16 또는 9보다 적은 숫자여야 한다.28개의 실제 비탄젠트를 가진 또 다른 사분위는 두 개의 비병렬 라인에 접하는 고정 축 길이의 타원 중심부에 의해 형성될 수 있다.^[2]시오다(1995)는 입방면을 투영하여 형성된 28개의 비탄젠트로 사분위를 다르게 만들었다. 시오다의 곡선에 대한 비탄젠트 중 27개는 실제인 반면 28개는 투영면에서 무한대의 선이다.

예

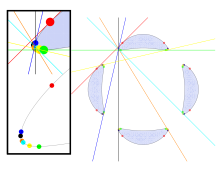
28개의 실제 비탄젠트가 있는 또 다른 곡선인 트로트 곡선은 4개의 다항식을 만족하는 점 집합(x,y)이다.

${\displaystyle \displaystyle 144(x^{4}+y^{4})-display(x^{2}+y^{2})+350x^{2}+81=0.}$

이 점들은 속 3이 있고 28개의 진짜 이항체가 있는 비정렬 사분위 곡선을 형성한다.^[3]

플뤼커와 블럼과 기넌트의 예처럼 트로트 곡선은 4도의 곡선에 대한 최대 숫자인 4개의 분리된 난자를 가지고 있으며, 따라서 M-곡선이 된다.네 개의 난자는 여섯 쌍의 서로 다른 난자로 분류될 수 있다. 각 난자의 쌍에 대해 두 개의 난자를 구분하는 두 개의 난자와 그렇지 않은 두 개의 난자가 쌍의 두 난자에 모두 닿는다.또한 각 타원은 평면의 비콘벡스 영역을 경계하며, 경계에서 비콘벡스 부분에 걸쳐 있는 하나의 비탕겐트를 가진다.

다른 구조물에 대한 연결

사분위 곡선까지의 이중 곡선은 원시 곡선의 28개 비탄젠트에 이중인 28개의 실제 일반 더블 포인트를 가지고 있다.

사분위의 28개의 이탄젠트는 또한 형태의 기호와 일치하도록 배치될 수 있다.

${\displaystyle \left[{\put{array}{ccc}a&b&c\\d&e&f\\end{array}\오른쪽]}$

a, b, c, d, e, f가 모두 0이거나 1이고

광고 + be + cf = 1(^[4]모드 2)

a, b, c, d, e, f의 선택은 64개가 있지만 이 중 28개만이 홀수를 산출한다.또한 a, b, c를 파노 평면의 점 및 d, e, f의 점의 균일한 좌표로 해석할 수 있다. 합이 홀수인 조건은 점과 선이 서로 닿지 않도록 요구하는 것과 동등하며, 점 및 선 tha의 28쌍이 있다.만지지 않는다.

비사건적인 점선 쌍으로부터 분리된 파노 평면의 점과 선은 삼각형을 형성하며, 사분위의 이탄젠트는 파노 평면의 28개 삼각형과 일치한다고 간주되어 왔다.^[5]파노 평면의 레비 그래프는 헤우드 그래프로, 파노 평면의 삼각형이 6 사이클로 표현된다.히우드 그래프의 28 6주기는 콕시터 그래프의 28 정점에 해당한다.^[6]

사분위의 28개 비탄젠트는 또한 도-2 델 페조 표면의 56개 선 ^[5]쌍과 28개의 홀수 세타 특성과 일치한다.

입방체 위의 27개 선과 4개의 카노닉 육분의 120개 삼중수소 평면과 함께 사분위에 있는 28개의 이탄젠트는 블라디미르 아놀드의 의미, 특히 맥케이 서신의 한 형태로서 "삼위성"을 형성하며,^[7][8][9] 삼위체에서 논의된 바와₇ 같이 E와 E를₈ 포함한 많은 다른 물체와 관련될 수 있다.

메모들

참조

• Blum, R.; Guinand, A. P. (1964). "A quartic with 28 real bitangents". Canadian Mathematical Bulletin. 7 (3): 399–404. doi:10.4153/cmb-1964-038-6.
• TheCayley, Arthur (1879), "On the bitangents of a quartic", Salmon's Higher Plane Curves, pp. 387–389 Athur Cayley, Andrew Russell Porsyth, Ed, The University Press, 1896, 11, 페이지 221–223의 수학 논문집.
• Gray, Jeremy (1982), "From the history of a simple group", The Mathematical Intelligencer, 4 (2): 59–67, doi:10.1007/BF03023483, MR 0672918, S2CID 14602496. 재인쇄.
• Manivel, L. (2006), "Configurations of lines and models of Lie algebras", Journal of Algebra, 304 (1): 457–486, arXiv:math/0507118, doi:10.1016/j.jalgebra.2006.04.029, S2CID 17374533.
• Plücker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie, Berlin: Adolph Marcus.
• 케일리가 인용한 바와 같이Riemann, G. F. B. (1876), "Zur Theorie der Abel'schen Funktionen für den Fall p = 3", Ges. Werke, Leipzig, pp. 456–472.
• Shioda, Tetsuji (1995), "Weierstrass transformations and cubic surfaces" (PDF), Commentarii Mathematici Universitatis Sancti Pauli, 44 (1): 109–128, MR 1336422
• Trott, Michael (1997), "Applying GroebnerBasis to Three Problems in Geometry", Mathematica in Education and Research, 6 (1): 15–28.