육각결정군
Hexagonal crystal family| 크리스털 시스템 | 삼각형 | 육각형 | |
|---|---|---|---|
| 격자계통 |  림보헤드랄 |  육각형 | |
| 예 |  돌로마이트 |  α-쿼츠 |  베릴 |
결정학에서 육각 결정과는 6개의 결정 계열 중 하나로, 2개의 결정계(헥사각과 삼각)와 2개의 격자계(헥사각과 림보헤드랄)를 포함한다. 일반적으로 혼란스럽지만 삼각 결정 시스템과 회전 격자 시스템은 동등하지 않다(아래 단면 결정 시스템 참조).[1] 특히 삼각대칭을 가진 결정체가 있지만 육각형 격자(α-쿼츠 등)에 속한다.
육각결정 계열은 12개 점군으로 구성되는데, 이들 우주군 중 하나 이상이 육각 격자를 밑단 격자로 하고, 육각결정계통과 삼각결정계통의 결합이다.[2] 그것과 연관된 52개의 우주 집단이 있는데, 정확히 브라바이스 격자가 육각형 또는 심복형인 집단이 있다.
격자 시스템
육각 결정 계열은 육각과 심복의 두 개의 격자 계통으로 구성되어 있다. 각 격자 시스템은 하나의 Bravais 격자로 구성된다.
| 브라바이스 격자 | 육각형 | 림보헤드랄 |
|---|---|---|
| 피어슨 기호 | hP | hR |
| 육각형 단위 세포 |  | 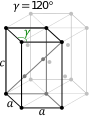 |
| 림보헤드랄 단위 세포 |  | 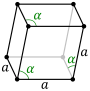 |
육각형 계열에서 결정체는 두 개의 축(a by a)과 120°의 각( angle)과 두 개의 기본 축에 수직인 높이(c, a와 다를 수 있음)를 가진 우측 롬빅 프리즘 단위 셀에 의해 통상적으로 설명된다.
Rhombohedral Bravais 격자를 위한 육각형 단위 셀은 R 중심 셀로, 단위 셀의 대각선 한 몸체를 차지하는 두 개의 추가 격자 지점으로 구성된다. 이렇게 하는 데는 두 가지 방법이 있는데, 이것은 같은 구조를 나타내는 두 개의 표기라고 생각할 수 있다. 일반적인 소위 횡방향 설정에서 추가 격자점은 좌표(좌표)에 있다.½3, ½3, ½3) 및 (½, ½3, ½3)의 경우, 대체 역방향 설정에서는 좌표(½3, ½3, ½3)와 (2/3, ½3, ½3)에 있다.[3] 두 경우 모두 단위 셀당 격자 점수는 총 3개이며 격자는 기본이 아니다.
육각 결정 계열의 브라바이스 격자도 심복 축으로 설명할 수 있다.[4][5] 단위 세포는 림보헤드론이다(림보헤드랄 격자 이름을 알 수 있다). 이것은 매개변수 a = b = c; α = β = = 90°[6]인 단위 셀이다. 실제로 두 90° 각도로 좌표계를 다루기 쉽기 때문에 육각형 설명이 더 흔하게 사용된다. 단, 이 셀은 결정 격자의 3m 대칭을 나타내기 때문에 교과서에 (음경 격자용) 회전 축이 자주 표시된다.
육각 Bravais 격자용 rhomboedral 단위 셀은 D 중심[7] 셀로, 좌표(½3, ½3, ½3, ½3)와 (2/3, ½3)로 단위 셀의 한 몸체 대각선을 차지하는 두 개의 추가 격자 지점으로 구성된다. 그러나 그러한 서술은 거의 사용되지 않는다.
크리스털 시스템
| 크리스털 시스템 | 점 그룹의 필요한 대칭 | 점 그룹 | 공간 그룹 | 브라바이스 격자 | 격자계통 |
|---|---|---|---|---|---|
| 삼각형 | 1 3축 회전 | 5 | 7 | 1 | 림보헤드랄 |
| 18 | 1 | 육각형 | |||
| 육각형 | 1 6배 회전축 | 7 | 27 |
육각결정 계열은 삼각형과 육각형의 두 개의 결정계로 이루어져 있다. 결정 시스템은 점 그룹 자체와 해당 공간 그룹이 격자 시스템에 할당되는 점 그룹 집합이다(Crystal system#Crystal 클래스의 표 참조).
삼각결정계는 단일 3배 회전축을 갖는 5점 그룹으로 구성되며, 우주군 143~167을 포함한다. 이들 5개 점군에는 7개의 해당 공간군(R로 표시됨)이 심복면 격자계통에 할당되고 18개의 해당 공간군(P로 표시됨)이 육각형 격자계통에 할당된다. 따라서 삼각 결정 체계는 점 그룹이 둘 이상의 격자 체계를 가진 유일한 결정 체계로서 공간 그룹과 연관되어 있다.
육각결정계는 단일 6배 회전축을 갖는 7개 점군으로 구성된다. 이들 7개 점군에는 27개의 공간군(168~194)이 있으며, 모두 육각 격자계통에 할당되어 있다.
삼각결정계
이 결정체계의 5개 점 그룹은 국제 번호와 표기법, 이름 및 예시 결정으로 된 우주 그룹과 함께 아래에 열거되어 있다.[8][9][10]
| 스페이스 그룹 번호. | 점군 | 유형 | 예 | 공간 그룹 | |||||
|---|---|---|---|---|---|---|---|---|---|
| 이름[11] | 인틀 | 쇤. | 궤도를 돌다. | 콕스. | 육각형 | 림보헤드랄 | |||
| 143–146 | 삼각 피라미드 | 3 | C3 | 33 | [3]+ | 반동형성의 극성의 | 탄수화물, 자로사이트 | P3, P31, P32 | R3 |
| 147–148 | 림보헤드랄 | 3 | C3i(S6) | 3× | [2+,6+] | 중심 대칭의 | 돌로마이트, 일메나이트 | P3 | R3 |
| 149–155 | 삼각 사다리꼴 | 32 | D3 | 223 | [2,3]+ | 반동형성의 | 아브후라이트, 알파 사분위( (, 154), 신나바르 | P312, P321, P3121, P3121, P3122, P3212 | R32 |
| 156–161 | 직교피라미드 | 3m | C3v | *33 | [3] | 극성의 | 쇼울, 세라이트, 투르말린, 알루나이트, 탄탈산 리튬 | P3m1, P31m, P3c1, P31c | R3m, R3c |
| 162–167 | 치태성 치상 | 3m | D3d | 2*3 | [2+,6] | 중심 대칭의 | 안티몬, 헤마이트, 코런덤, 석회석, 비스무트 | P31m, P31c, P3m1, P3c1 | R3m, R3c |
육각결정계
이 결정체계의 7개 점군(결정계급)[2][12]은 아래에 열거되어 있으며, 그 뒤에 헤르만-마우긴 또는 국제 표기법과 쇤파리 표기법, 광물 예(있는 경우)가 있다.
| 스페이스 그룹 번호. | 점군 | 유형 | 예 | 공간 그룹 | ||||
|---|---|---|---|---|---|---|---|---|
| 이름[11] | 인틀 | 쇤. | 궤도를 돌다. | 콕스. | ||||
| 168–173 | 육각 피라미드 | 6 | C6 | 66 | [6]+ | 반동형성의 극성의 | 네팔라인드, 캔크라인드 | P6, P61, P65, P62, P64, P63 |
| 174 | 삼위일체 | 6 | C3h | 3* | [2,3+] | 월계수염과 붕산 | P6 | |
| 175–176 | 육각형 디피라미달 | 6/m | C6h | 6* | [2,6+] | 중심 대칭의 | 아파타이트, 바나딘나이트 | P6/m, P63/m |
| 177–182 | 육각 사다리꼴 | 622 | D6 | 226 | [2,6]+ | 반동형성의 | 칼실라이트와 고쿼츠 | P622, P6221, P6225, P6222, P6224, P622, P6223 |
| 183–186 | 디헥사각 피라미드 | 6mm | C6v | *66 | [6] | 극성의 | 그린록라이트, 우르츠라이트[13] | P6mm, P6cc, P63cm, P63mc |
| 187–190 | 치트지질 쌍극자살 | 6㎡ | D3h | *223 | [2,3] | 베니토이트 | P6㎡, P6c2, P62m, P62c | |
| 191–194 | 디헥사형 디피라미달 | 6/10 | D6h | *226 | [2,6] | 중심 대칭의 | 베릴 | P6/mmm, P6/mcc, P63/mcm, P63/mmc |
육각형 근접 포장
육각형 클로즈패킹(hcp)은 밀도가 가장 높은 원자패킹의 두 가지 단순한 형태 중 하나이며, 다른 하나는 얼굴 중심의 입방체(fcc)이다. 그러나 FCC와는 달리 격자점 세트가 두 개 없기 때문에 브라바이스 격자가 아니다. 대신 각 격자점과 연관된 2원자 모티브(약 (½3, ½)의 추가 원자)를 사용하여 육각형 브라바이스 격자로부터 구성할 수 있다.[14]
2차원으로
육각형 브라바이스 격자는 2차원, 즉 육각형 격자는 1개뿐이다.
| 브라바이스 격자 | 육각형 |
|---|---|
| 피어슨 기호 | hp |
| 단위세포 |  |
참고 항목
참조
- ^ 한 (2002)
- ^ a b Dana, James Dwight; Hurlbut, Cornelius Searle (1959). Dana's Manual of Mineralogy (17th ed.). New York: Chapman Hall. pp. 78–89.
- ^ Edward Prince (2004). Mathematical Techniques in Crystallography and Materials Science. Springer Science & Business Media. p. 41.
- ^ "Page not found - QuantumWise". quantumwise.com.
{{cite web}}: Cite는 일반 제목(도움말)을 사용한다. - ^ "Medium-Resolution Space Group Diagrams and Tables". img.chem.ucl.ac.uk.
- ^ Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics (1st ed.). p. 119. ISBN 0-03-083993-9.
- ^ 한(2002년), 페이지 73
- ^ Pough, Frederick H.; Peterson, Roger Tory (1998). A Field Guide to Rocks and Minerals. Houghton Mifflin Harcourt. p. 62. ISBN 0-395-91096-X.
- ^ Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th ed.). pp. 78–89. ISBN 0-471-80580-7.
- ^ "Crystallography and Minerals Arranged by Crystal Form". Webmineral.
- ^ a b 한(2002년), 페이지 794년
- ^ "Crystallography". Webmineral.com. Retrieved 2014-08-03.
- ^ "Minerals in the Hexagonal crystal system, Dihexagonal Pyramidal class (6mm)". Mindat.org. Retrieved 2014-08-03.
- ^ Jaswon, Maurice Aaron (1965-01-01). An introduction to mathematical crystallography. American Elsevier Pub. Co.
추가 읽기
- Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. International Tables for Crystallography. Vol. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.
외부 링크
 위키미디어 공용의 육각형 격자 관련 매체
위키미디어 공용의 육각형 격자 관련 매체- 광물학 데이터베이스




