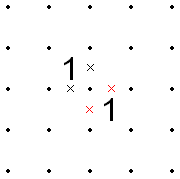슬라이더링크

Slitherlink
중간 정도의 난이도의 슬라이더링크 퍼즐(솔루션)

Sliderlink (펜스, 타케가키, 루프 더 루프, 루피, 오로보로스, 수리자, 도티 딜레마로도 알려져 있음)는 출판사 Nikoli가 개발한 논리 퍼즐이다.

규칙.

슬라이더링크는 점의 직사각형 격자 위에서 재생됩니다.점으로 이루어진 정사각형에는 숫자가 들어가 있습니다.목적은 선이 느슨하지 않고 단순한 루프를 형성하도록 수평 및 수직으로 인접한 점을 연결하는 것입니다.또한 정사각형 안에 있는 숫자는 4개의 변 중 루프의 세그먼트 수를 나타냅니다.

표준 그리드 대신 다른 유형의 평면 그래프를 사용할 수 있으며, 정점당 또는 폴리곤당 정점의 수가 달라집니다.이러한 패턴에는 눈송이, 펜로즈, 라베스, 알테어 타일링이 포함됩니다.이러한 규칙은 교차로에서 가능한 경로의 수 및/또는 각 폴리곤에 대한 변의 수를 변경하여 복잡성을 증가시킵니다. 그러나 솔루션에는 유사한 규칙이 적용됩니다.

해결 방법

표기법

셀 주위의 회선 수가 셀 내의 회선 수와 일치할 때마다 다른 잠재적인 회선은 삭제해야 합니다.이것은, 통상은 빈 행에 X 마크를 붙이는 것으로 표시됩니다.

Sliderlink를 해결할 때 또 다른 유용한 표기법은 인접한 두 줄 사이에 90도 호를 표시하여 두 줄 중 하나를 정확히 채워야 함을 나타냅니다.관련 표기법은 인접한 선 사이의 이중 호로, 두 선을 모두 채우거나 둘 다 채워야 함을 나타냅니다.이러한 표기는 솔루션에 필요하지 않지만 솔루션을 도출하는 데 도움이 될 수 있습니다.

구석에 있는 2 주위에 있는 호 표기법.

아래의 방법 중 대부분은 호 표기법을 사용하여 두 가지 간단한 단계로 나눌 수 있습니다.

각 점에 정확히 2줄 또는 0줄

Sliderlink에서 많은 연산을 할 수 있는 중요한 점은 모든 점에 정확히 2개의 회선이 연결되어 있거나 회선이 없다는 것입니다.따라서 가장자리나 모서리가 아닌 그리드의 중심에 있는 점에 X'd 아웃된 세 개의 들어오는 선이 있는 경우, 네 번째 점도 X'd 아웃이어야 합니다.그 이유는 점에는 1개의 선만 있을 수 없기 때문입니다.그 점으로부터의 출구 루트는 없습니다.마찬가지로, 모서리가 아닌 그리드의 모서리에 있는 점에 X'd 아웃된 두 개의 들어오는 선이 있는 경우, 세 번째도 X'd 아웃이어야 합니다.그리드의 한 모서리에 X'd 아웃된 들어오는 선이 있는 경우, 다른 쪽도 X'd 아웃이어야 합니다.

이 간단한 규칙을 적용하면 연산이 더욱 복잡해집니다.이러한 간단한 패턴을 인식하면 Sliderlink 퍼즐을 푸는 데 큰 도움이 됩니다.

모서리

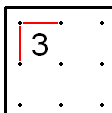
  • 1이 코너에 있는 경우, 실제 코너의 라인은 X'd 아웃이 될 수 있습니다.이는 해당 코너에 들어간 라인이 다시 1을 통과하지 않는 한 그 코너를 벗어날 수 없기 때문입니다.이는 같은 코너의 1박스로 이어지는 두 줄이 X'd 아웃된 경우에도 적용됩니다.
구석에 1이 있다.
  • 3이 코너에 있는 경우, 그 상자의 바깥쪽 가장자리 2개를 채울 수 있습니다.그렇게 하지 않으면 위의 규칙을 어길 필요가 있기 때문입니다.
구석에 3점.
  • 2가 구석에 있는 경우 경계에 있는 2에서 두 줄이 떨어져 있어야 합니다.
구석에 2가 있다.

1이 있는 정사각형에 대한 규칙

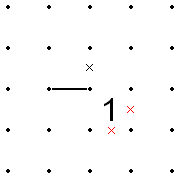
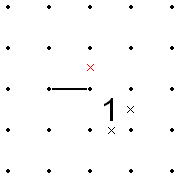
  • 선이 1의 한 구석에 있고, 그 선이 연속할 수 있는 나머지 3개의 방향 중 하나가 1의 한 변이 아닌 다른 방향이 이미 알려진 공백일 경우, 그 모서리 반대쪽의 1의 두 변은 X'd아웃될 수 있습니다.
선 옆에 1이 있다.
  • 이는 반대로도 적용됩니다.즉, 선이 1의 구석에 있고 1의 두 개의 반대쪽 가장자리가 이미 X'd되어 있는 경우 X가 1의 모든 면에 배치되기 때문에 선은 1에서 벗어날 수 없습니다.
줄 옆에 1이 있다(대면)
  • 2개의 1이 대각선으로 인접해 있는 경우, 그 2개의 셀 주위의 8개의 세그먼트 중 공통의 엔드 포인트(1s가 공유하는 포인트)를 공유하는 4개의 세그먼트의 「내부」세트 또는 4개의 세그먼트의 다른 「외부」세트 중 하나가 모두 X'd아웃이 되어야 합니다.따라서 한 개의 1에 있는 두 개의 내부 또는 외부 세그먼트가 X'd인 경우, 다른 1의 각 내부 또는 외부 세그먼트도 X'd여야 합니다.
대각선으로 인접한 1s
대각선으로 인접한 1s
  • 2개의 1이 그리드의 가장자리를 따라 인접해 있는 경우, 그 사이의 선은 X'd가 될 수 있습니다. 왜냐하면 가장자리에 도달했을 때 계속되는 방향이 없기 때문입니다.

2가 있는 제곱에 대한 규칙

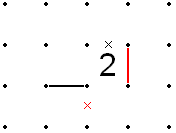
2에 X'd의 주변선이 있는 경우 X'd 출력선에 인접하지 않은 두 모서리 중 하나에 들어오는 선은 2에서 직각으로 바로 나갈 수 없습니다. 그러면 2 주위에 있는 두 개의 선이 불가능하기 때문에 X'd가 될 수 있습니다.즉, 착신 회선은, 2 의 한쪽 또는 다른 한쪽에서 속행할 필요가 있습니다.즉, 2개의 두 번째 라인은 원래 X'd 라인에 인접한 유일하게 남은 자유 측에 있어야만 입력이 가능하다는 것을 의미합니다.
반대로, 2의 한쪽 면에 라인이 있고 인접한 X'd 출력 라인이 있는 경우, 두 번째 라인은 나머지 두 개의 측면 중 하나에 있어야 하며 반대쪽 모서리(양쪽 방향)에서 나와야 합니다.만약 두 개의 출구 중 하나가 X'd 아웃이라면 다른 루트로 가야 합니다.

선 옆에 2가 있다.

3의 제곱에 대한 규칙

  • 3이 0에 수평 또는 수직으로 인접해 있는 경우, 0에 닿는 것을 제외한 3의 모든 모서리를 채울 수 있습니다.또, 인접한 박스에 수직인 2개의 라인을 충전할 수 있다.
0에 인접한 A 3
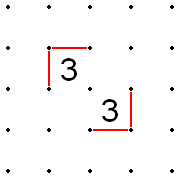
  • 2개의 3이 수평 또는 수직으로 서로 인접해 있는 경우 공통 가장자리를 채워야 합니다.다른 옵션은 다른 선에 연결할 수 없는 닫힌 타원형뿐이기 때문입니다.둘째, 그룹의 두 개의 외부 라인(공통 라인과 평행)을 입력해야 합니다.세 번째, 3s를 통과하는 선은 항상 "S"자 모양으로 둘러쌉니다.따라서 3s 사이의 직선이 일직선이 될 수 없고, 중간에서 일직선이 되는 변은 X'd 아웃이 될 수 있다.
인접한 2개의 3s
  • 3이 대각선으로 0에 인접해 있는 경우, 3의 양쪽 모서리에 해당하는 부분을 채워야 합니다.그 이유는 어느 한쪽이 열려 있는 경우, 0 의 구석에 끝나는 회선은 갈 곳이 없기 때문입니다.이것은 3-in-a-corner 규칙과 비슷합니다.
대각선 3은 0 옆에 있다.
  • 마찬가지로, 3의 각도가 X의 양방향으로 그 각도에서 벗어나는 경우, 그 각도와 만나는 3의 양쪽은 채워져야 합니다.이는 3개의 두 변 중 하나가 열려 있으면 다른 변은 채워야 하지만(3개의 변은 열려 있는 변만 가질 수 있기 때문에) 해당 모서리에서는 3X를 충족하기 때문입니다.이는 그리드 상의 각 점이 정확히 2개 또는 0개의 선을 가지고 있어야 하기 때문에 불가능합니다.
  • 선이 3의 모서리에 도달한 경우, 3의 양쪽에는 해당 모서리가 인접하지 않은 선이 있어야 합니다. 왜냐하면 3의 유일한 빈 공간이 인접하지 않은 경우 모서리에는 3개의 선이 연결되어 있기 때문입니다.또, 라인이 도달한 코너의 3으로부터 멀어지는 세그먼트는 비워 둘 필요가 있습니다.이 세그먼트가 채워져 있는 경우, 3의 나머지 2개의 미결정측 모두 라인을 포함할 수 없습니다.
한 줄 옆에 3이 있어요.

3s와 2s의 대각선

  • 두 개의 3이 대각선으로 인접해 있는 경우 공통점에 도달하지 않는 가장자리를 채워야 합니다.
2개의 대각선 3s.
  • 마찬가지로, 2개의 3s가 같은 대각선상에 있지만 2s(및 2s만)로 구분되는 경우, 3s의 바깥쪽 가장자리는 대각선으로 인접해 있는 것처럼 채워야 합니다.
대각선 3s와 대각선 2를 사이에 두고
  • 대각선에 일련의 2s가 있고 각진 선이 시리즈의 한쪽 끝에서 두 개의 모서리와 만나는 경우 일치하는 각진 선을 영상 시리즈 위로 그릴 수 있습니다.
1개 또는 여러 개의 대각선 2s를 가리키는 2개의 채워진 선으로 끝납니다.
  • 선이 하나 이상의 2s를 포함하는 대각선의 시작점(A)에 도달하여 3으로 끝나는 경우, 3의 먼 구석(대각선의 A에서 가장 빠른 부분)의 양쪽을 채워야 한다.이것이 사실이 아닌 경우, 3의 근방 모서리 양쪽을 채워야 한다는 것을 의미하며, 이는 대각선 시작 부분의 2를 포함하여 모든 2의 근방 모서리를 채워야 한다는 것을 의미하며, 이는 시작점(A)에 도달한 선과 충돌하기 때문에 불가능합니다.
대각선 2는 3으로 끝납니다.

3과 1의 대각선

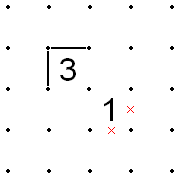
  • 1과 3이 대각선 방향으로 인접해 있고 1의 바깥쪽 두 변이 X'd가 되어 있는 경우, 3의 바깥쪽 두 변을 채워야 합니다.
3과 1의 대각선
  • 그 반대도 마찬가지입니다.3의 바깥쪽 두 모서리가 채워지면 1의 바깥쪽 두 모서리가 X'd가 되어 있어야 합니다.
3과 1의 대각선

2로 시작하는 대각선

  • 선이 2의 모서리에 도달하고 선이 2의 2개의 접속측 중 하나를 통과해야 하는 경우, 2의 다른 2개의 접속측 중 하나를 정확히 채우고 그 선은 대각선으로 인접한 정사각형의 2개의 접속측 중 하나를 통과해야 합니다.
Slitherlink-Diagonal-Starting-With-2-A.jpg
Figure 2, 'Diagonals starting with 2' rule, on the Slitherlink page.jpg

닫힌 영역에 대한 규칙

격자의 영역이 닫히고('회피'할 수 없는' 선'이 비어 있지 않은 경우) 영역 밖에서 시작하는 영역에 들어가는 선의 수는 0이 아니어야 합니다(홀수 개수의 선은 영역 내에서 홀수 개수의 세그먼트 끝을 의미하므로 모든 세그먼트 끝은 연결할 수 없습니다).이러한 회선이 없는 경우, 영역내의 회선은 외부의 회선과 접속할 수 없기 때문에, 해결은 불가능합니다).대부분의 경우 이 규칙에 의해 실행 가능한 옵션이1개 이상 없어집니다.

아래 그림에서 왼쪽 상단에 있는 선은 아래로 진행하든 오른쪽으로 진행하든 격자의 오른쪽 상단 영역을 닫습니다.오른쪽 선(3의 양 옆)이 닫힌 영역에 들어갔습니다.규칙을 충족시키려면 첫 번째 행이 영역을 입력해야 하며 두 번째 행이 영역을 두 번째로 입력해서는 안 됩니다.(닫힌 영역의 경계도 퍼즐의 나머지 부분을 닫기 때문에 이 규칙은 더 큰 왼쪽 아래 영역에도 적용될 수 있습니다.규칙을 적용하려면 경계를 통과하는 선을 세기만 하면 됩니다.)

Slitherlink-closed-area-rule.png

조던 곡선 정리

매우 어려운 퍼즐에서는 닫힌 곡선 밖에서 시작하고 끝나는 열린 곡선은 닫힌 곡선과 짝수만큼 교차해야 한다는 조던 곡선 정리를 사용할 수 있습니다.특히, 그리드의 모든 행에는 짝수의 수직선이 있어야 하며, 열에는 짝수의 수평선이 있어야 합니다.이러한 그룹 중 하나에서 하나의 잠재적 선분만 알 수 없는 경우 이 정리를 사용하여 루프의 일부인지 여부를 판단할 수 있습니다.

이 정리를 사용하는 데 도움이 되는 간단한 전략은 외부와 내부 영역을 "도색"하는 것입니다.두 개의 외부 셀 또는 두 개의 내부 셀이 서로 옆에 있는 경우, 두 셀 사이에 선이 없음을 알 수 있습니다.반대로도 마찬가지입니다.두 셀 사이에 선이 없는 것을 알고 있는 경우는, 그 셀이 같은 「색」(내부 또는 외부 양쪽 모두)이어야 합니다.마찬가지로 외부 셀과 내부 셀이 인접해 있는 경우 둘 사이에 채워진 선이 있어야 합니다.반대도 마찬가지입니다.

정답이 1개뿐인 퍼즐의 규칙

  • 솔루션 내의 두 점 사이에 A와 B라는 정확히 두 개의 가능한 경로가 있는 경우(직선으로 도달했거나 도달해야 하는 두 점) 및 A를 포함하는 솔루션이 B와 함께 작동해야 하며, 그 반대의 경우 B는 올바른 경로이며, 솔루션은 A에 포함된 지점을 통과해야 하지만 B는 통과해야 합니다.

아래 그림에서 용액이 2의 위쪽과 오른쪽을 통과할 수 있는 경우, 2의 위쪽과 오른쪽의 정사각형은 구속되지 않기 때문에 2의 아래쪽과 왼쪽을 통과하는 것 이외에는 완전히 동일한 용액이 존재해야 합니다.또한 용액은 2의 오른쪽 상단 모서리를 통과해야 합니다.그렇지 않으면 2의 오른쪽 상단 모서리를 통과하는 것 이외에는 완전히 동일한 다른 용액이 존재해야 합니다.

Slitherlink-unique-solution-rule-1-v2.jpg

모서리에 2가 있고 두 개의 비직교적으로 인접한 정사각형이 구속되지 않은 경우 아래와 같이 선을 그릴 수 있습니다.(그림에서 물음표는 임의의 숫자 또는 빈칸을 나타내지만 숫자는 2 또는 3만 됩니다.해답이 1개뿐인 퍼즐은 2개의 비직교적으로 인접한 정사각형과 대각선으로 인접한 0 또는 1을 가진 구석에 2를 둘 수 없습니다.)

Slitherlink-Unique-Solution-1b-v2.jpg
  • 두 점 사이에 두 개의 경로가 있어 하나의 솔루션을 포함하는 솔루션이 다른 솔루션과 함께 작동해야 하는 경우 두 경로를 모두 제외할 수 있습니다.

아래 그림에서 동그라미로 둘러싸인 점들은 점들 사이의 직접 선으로 연결될 수 있으며, 점들의 왼쪽으로 뻗은 정사각형의 다른 세 변을 가로지르는 선으로도 연결될 수 있습니다.(빨간색 선은 무시한 채) 솔루션의 나머지 부분은 동일할 수 있습니다.솔루션의 나머지 부분은 동일하기 때문에 두 경로는 모두 제외됩니다.

Slitherlink-unique-solution-rule-2.jpg

역사

슬라이더링크는 니콜리의 독창적인 퍼즐이다; 그것은 퍼즐 커뮤니케이션 니콜리 #26 (1989년 6월)에 처음 등장했다.편집자는 거기에 투고된 두 개의 오리지널 퍼즐을 조합했다.처음에는 모든 정사각형에 숫자가 들어있었고 모서리는 루프를 형성할 필요가 없었습니다.

비디오 게임

슬라이더링크 퍼즐은 여러 플랫폼의 비디오 게임에 포함되어 있습니다.Slider Link라는 이름의 게임이 2000년 [1]반다이에 의해 일본에서 Wonderwan 휴대용 콘솔용으로 출판되었다.슬라이더링크 퍼즐은 2001년 게임보이 닌텐도 파워 카트리지의 Success for the Game Boy의 게임인 Loppi Puzzle Magazine: Kangaeru Puzle 시리즈에 스도쿠 퍼즐과 노노그램 퍼즐과 함께 포함되었다.[2]슬레이더링크 게임은 닌텐도 DS 핸드헬드 게임기에도 등장했으며 허드슨 소프트는 2006년 11월 16일 퍼즐 시리즈 Vol. 5: Sliderlink를 일본에서 발매했으며 [3]2007년 6월 17일 북미에서 발매된 Nikoli 퍼즐 컴필레이션 Brain Buster Pak에 Sliderlink를 포함한 Agetec을 발매했다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ WonderSwan용 슬라이드 링크 - 게임FAQ
  2. ^ 롭피 퍼즐 매거진 강개루 퍼즐 게임보이 컬러 - 게임FAQ
  3. ^ 퍼즐 - 브레인버스터 퍼즐팩 - Agetec, Inc.

외부 링크