반정형 폴리토프

고셋의 숫자

3D 허니컴
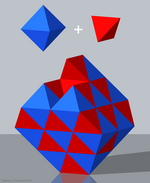단순 사방면체크	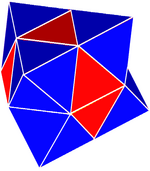복합 사방면체크
4D 폴리토페스
사방면체	팔면체	Tetricosaheadric

기하학에서, 소럴드 고셋의 정의에 따르면, 반정형 폴리토프는 보통 정점 통일형이고 그것의 모든 면이 규칙적인 폴리토페스로 간주된다.E.L. Elte는 1912년에 더 긴 목록을 더 넓은 정의를 포함하는 하이퍼스페이스의 반정형 폴리토페스로 편집했다.

고셋 리스트

3차원 공간 이하에서는 모든 균일한 폴리곤이 규칙적이어야 하기 때문에 반정형 폴리토페와 균일한 폴리토페라는 용어는 같은 의미를 갖는다.그러나 모든 균일한 다면체들이 규칙적인 것은 아니기 때문에, 3개 이상의 치수의 반정형 다면체의 수는 같은 치수의 균일한 다면체의 수보다 훨씬 적다.

3개의 볼록 반경 4-폴리탑은 정류된 5-셀, 스너브 24-셀, 정류된 600-셀이다.고차원의 유일한 반정형 폴리토페스는 k₂₁ 폴리토페즈인데, 여기서 정류된 5-셀은 k = 0의 특수한 경우다.이것들은 모두 고셋에 의해 나열되었지만, 4차원의 마카로프(1988)와 더 높은 차원의 블라인드 & 블라인드(1991)의 작업이 있기 전에는 이 목록의 완전성에 대한 증거가 발표되지 않았다.

고셋의 4폴리탑(이름이 괄호 안에 들어 있음)

수리된 5-셀(Tetroctaheadric),

정류된 600셀(옥티코사헤드릭),

Snub 24-cell(Tetricoshedric), 또는

고차원의 반정형 E-폴리탑

5데미큐브(5ic 반정규직), 5데미코프, 파운드

polytope₂₁ (6-ic semi-rumular), 6-tope (6-tope

3₂₁ 폴리토프(7-ic 반정규격), 7-148,

4개의₂₁ 폴리토프(8-ic 반정규격), 8개의 폴리토프,

유클리드 허니컴

반정형 폴리토페스는 반정형 벌집까지 확장할 수 있다.반정형 유클리드 허니콤은 사면체-옥타면체 허니콤(3D), 자정형 대체 큐빅 허니콤(3D), 5면체₂₁ 허니콤(8D)이다.

고셋 허니컴:

1. 사면체-옥타면체 벌집 또는 대체입방형 벌집형 벌집형(단순 사면체크), £(또한 quasiregular polytope)
2. Gyrated 교대 입방형 벌집(복합 테트로크타헤드체크),

반정형 E-허니콤:

• 벌집 5개₂₁(9-ic check)(8D 유클리드 벌집),

쌍곡선 허니컴

또한 정규 세포로만 구성된 쌍곡선 균일 벌집(Coxeter & Whitrow 1950)도 있으며, 다음과 같다.

• 쌍곡선 균일 벌집, 3D 벌집:
  1. 대체 오더-5입방 벌집, 파운드 (또한 쿼레겔 폴리토프)
  2. 사면체-옥타면체 벌집,
  3. 4면체-icosa-headron 벌집,
• 파라콤팩트 균일 벌집, 3D 벌집, 균일한 기울기를 셀로 포함하는:
  1. 수정 명령 6 사면체 벌집형
  2. 네모난 타일링 벌집,
  3. 수정 주문-4제곱 평방 타일링 벌집, 파운드
  4. 대체 주문-6입방 벌집, 파운드(도)
  5. 교대형 육각 타일링 벌집, 파운드
  6. 대체 주문-4 육각형 타일링 벌집, 파운드
  7. 대체 주문-5 육각 타일링 벌집, 파운드
  8. 교번주문-6 육각형 타일링 벌집, 파운드
  9. 교대제 사각 타일링 벌집, 파운드(도수치룰러)
  10. 큐빅 사각형 타일링 벌집,
  11. 순서-4 사각 타일링 벌집, =
  12. 사면삼각형 타일링 벌집,
• 9D 쌍곡선 포물선형 벌집:
  1. 벌집 6개₂₁(10-ic check),

참고 항목

• 반정형 다면체

참조

• Blind, G.; Blind, R. (1991). "The semiregular polytopes". Commentarii Mathematici Helvetici. 66 (1): 150–154. doi:10.1007/BF02566640. MR 1090169. S2CID 119695696.
• Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York: Dover Publications. ISBN 0-486-61480-8.
• Coxeter, H. S. M.; Whitrow, G. J. (1950). "World-structure and non-Euclidean honeycombs". Proceedings of the Royal Society. 201 (1066): 417–437. Bibcode:1950RSPSA.201..417C. doi:10.1098/rspa.1950.0070. MR 0041576. S2CID 120322123.
• Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
• Gosset, Thorold (1900). "On the regular and semi-regular figures in space of n dimensions". Messenger of Mathematics. 29: 43–48.
• Makarov, P. V. (1988). "On the derivation of four-dimensional semi-regular polytopes". Voprosy Diskret. Geom. Mat. Issled. Akad. Nauk. Mold. 103: 139–150, 177. MR 0958024.