양자점 접점

게이트 전압의 함수로서의 포인트 접점 컨덕턴스의 개략도.컨덕턴스는

2e^{2}/h

2e^{2}/h

2 /

h

의

(

에서

2e^{2}/\hbar

e

2e^{2}/\hbar

/

{\

{

style 2e^{2}/\hbar }

로

2e^{2}/\hbar

2e^{2}/\hbar

라벨링됨)에서 고원을 나타냅니다.

양자점 접점(QPC)은 전자파장(나노에서 마이크로미터)^[1]에 필적하는 폭의 2개의 넓은 전기전도 영역 간의 좁은 협착입니다.

QPC의 중요성은 메조스코프 시스템에서 탄도 전도도의 정량화를 증명한다는 사실에 있다.QPC의 컨덕턴스는 이른바 $2e^{2}/h$ 양자인 $e2$ / h(\ $displaystyle$ 2e $^{2}/h$ $2e^{2}/h$ 로 정량화됩니다.

양자점 접촉은 1988년 델프트 공과대학과 필립스^[2] 연구소의 네덜란드 팀과 카벤디시 ^[3]연구소의 영국 팀에 의해 처음 보고되었다.그들은 분할 게이트가 어떻게 2차원 전자 가스를 1차원으로 변환하는 데 사용될 수 있는지를 보여준 영국 그룹의 초기 연구에 기초하고 있다. 처음에는 실리콘에서^[4], 다음에는 비화 ^[5]^[6]갈륨에서.

이 양자화는 홀 컨덕턴스의 양자화를 연상시키지만 자기장이 없을 때 측정된다.0장 전도 양자화 및 자기장 적용에 대한 양자 홀 효과로의 원활한 전환은 기본적으로 수축 내 정수 개수의 전파 모드 간 전류 균등화의 결과이다.

제조

양자점 접점을 만드는 방법에는 여러 가지가 있습니다.그것은 도체 조각이 부서질 때까지 잡아당겨서 절단 접합으로 실현될 수 있다.한계점이 점 접점을 형성합니다.보다 제어된 방법으로 양자점 접점은 예를 들어 GaAs/AlGaAs 헤테로 구조에서 2차원 전자가스(2DEG)로 형성된다.적절한 형상의 게이트 전극에 전압을 인가함으로써 전자 가스를 국소적으로 고갈시킬 수 있어 양자점 및 양자점 접점 등 다양한 종류의 도전 영역을 2DEG 평면에 생성할 수 있다.QPC를 작성하는 또 다른 방법은 주사 터널링 현미경의 선단을 도체 표면에 가깝게 배치하는 것이다.

특성.

기하학적으로 양자점 접촉은 전자의 움직임에 대한 저항을 나타내는 가로 방향의 협착이다.전압 V $({$ $스타일$ V $})$ 를 점 접점에 $V$ 인가하면 전류가 흐르도록 유도하며, 이 전류의 $I=GV$ 는 I $=$ G $I=GV$ ({ $디스플레이 스타일$ I $=$ GV $I=GV$ 로 계산됩니다. $G$ 서 G $({디스플레이 스타일$ G $)$ 는 $G$ 접점의 전도도입니다.이 공식은 거시적 저항기에 대한 옴의 법칙과 유사합니다.그러나 여기에는 양자역학적 ^[7]분석이 필요한 작은 시스템 크기에서 비롯되는 근본적인 차이가 있다.

농도 차이에 의해 유도되는 점 접점을 통한 고전적인 탄도 수송.

k-공간에서 음영 영역에 의해 전달되는 양자점 접점을 통한 순 전류.그런 다음 1D

k_{y}=\pm n\pi /W

는 k

k_{y}=\pm n\pi /W

y = ±

µ

/

k_{y}=\pm n\pi /W

W({

displaystyle

k_

{y}=\pm

n\pi /

W

에서 수평선 쌍에 해당하며, n

k_{y}=\pm n\pi /W

1, 2, ., N은 페르미 ^[8]에너지가 허용하는 최대 모드 수입니다.

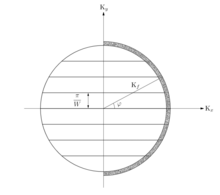
2차원 전자 가스에서 QPC를 연구하는 것이 가장 일반적입니다.이렇게 하면 점 접점의 기하학적 협착이 개구부를 통한 컨덕턴스를 1차원 시스템으로 전환합니다.더욱이, 전도성의 양자화를 초래하는 시스템의 양자역학적 설명이 필요하다.양자역학적으로는 점접점을 통과하는 전류가 협착에서 1D 서브랜드, 즉 횡방향 모드 간에 균등하게 분할된다.

앞에서 설명한 바와 같이 모드 간에 발생할 수 있는 전환은 고려되지 않음을 기술하는 것이 중요합니다.Landauer 공식은 실제로 이 가능한 변화를 표현하기 위해 일반화될 수 있다.

$G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ 2 $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ n , $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ n , $G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$ ( \ $displaystyle$ G = { 2 $e$ ^ { $2 over$ h } \ $sum$ _ { $n$ , $m$ } $T$ _ { $n$ , $m ^$ {2} $)$ ,

$T_{n,m}$ 서 T $T_{n,m}$ n , $T_{n,m}$ \ $displaystyle T_{n,m}$ 은 $T_{n,m}$ 모드n에서 m으로 전송될 확률이 0이 아닌 트랜지션 매트릭스입니다.

낮은 온도와 전압에서 전류에 기여하는 비포장 및 포장되지 않은 전자는 페르미 에너지/모멘텀/파장이라고 불리는 특정 에너지/모멘텀/파장을 가집니다.도파관에서와 같이, 양자점 접점의 횡방향 제한은 횡방향 운동의 "양자화"를 초래한다. 횡방향 운동은 연속적으로 변할 수 없지만 일련의 이산 모드 중 하나여야 한다.도파관 유추는 예를 들어 결함이나 포획 부위의 산란을 통해 일관성을 잃지 않는 한 적용할 수 있다.전자파는 건설적으로 간섭하는 경우에만 통과할 수 있으며, 일정한 수축폭에 대해 일정한 $모드$ N({ $displaystyle$ N $N$ 에서만 발생합니다. 이러한 양자 상태에 의해 전달되는 전류는 속도 곱하기 전자밀도의 곱입니다.이들 2개의 수량은 모드마다 다르지만 그 제품은 모드에 의존하지 않습니다.그 결과, 각 상태는 스핀 방향당 동일한 $e^{2}/h$ 의 $e^{2}/h$ e2 / $e^{2}/h$ (\ $displaystyle$ e $^{2}/h)$ 를 $e^{2}/h$ 총 $G=NG_{0}$ G $G=NG_{0}$ $G=NG_{0}$ $G=NG_{0}$ 0(\ $displaystyle$ G $=NG_{0$ 에 기여합니다.

이는 기본적인 결과입니다. 컨덕턴스는 임의의 값을 취하는 것이 아니라 컨덕턴스 $G_{0}=2e^{2}/h$ $G_{0}=2e^{2}/h$ $=$ $G_{0}=2e^{2}/h$ $G_{0}=2e^{2}/h$ $G_{0}=2e^{2}/h$ { $displaystyle G_{0$ } = $2 e^{2}/$ h $G_{0}=2e^{2}/h$ 의 배수( $전자$ 전하 e { $displaystyle$ e $}$ 및 $e$ 플랑크 $상수$ h { $style$ h $h$ 를 통해 표현됨)로 양자화됩니다.정수 $(\displaystyle$ N $)$ 은 $N$ 포인트 접점의 폭에 의해 결정되며 너비를 전자 파장의 절반으로 나눈 것과 거의 동일합니다.점 접점 폭(또는 GaAs/AlGaAs 헤테로 구조 장치의 경우 게이트 전압)의 함수로써 컨덕턴스는 점점 더 많은 모드(또는 채널)가 전자 전달에 기여함에 따라 계단 동작을 나타냅니다.스텝 하이트는 $G_{Q}$ Q $(\$ 에 의해 지정됩니다.

온도를 올리면 플라토판이 더 이상 분해되지 않을 때까지 유한한 기울기를 얻는다는 것을 실험적으로 알 수 있다.이것은 페르미-디락 분포의 열적 오염의 결과입니다.컨덕턴스 스텝은 T $T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K}$ E / $T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K}$ B $T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K}$ $T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K}$ ${$ $display style$ T $\lesssim \Delta$ E/ $4k_{\rm {B}}$ \ $about 4\;\mathrm {K}}$ 에 $T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K}$ 사라집니다(여기서 eE는 페르미레벨로 분할되는 서브밴드입니다).이것은 실험과 수치 ^[9]계산을 통해 확인된다.

양자점 접점에 인가되는 외부 자기장은 스핀 축퇴를 상승시켜 컨덕턴스의 반정수 단계로 이끈다.또한 기여하는 모드의 $수$ N(\ $style$ N $)$ 이 $N$ 작아집니다. $큰$ 자기장의 $,$ 양자 홀 효과 이론에 의해 주어진 협착 폭과는 $무관$ 합니다 $N$ .아직 완전히 이해되지 않은 흥미로운 특징은 0 $7G$ Q $(\$ 0.7)의 고원이다. $G_{Q$ 이른바 0.7 구조.

적용들

메소스코프 컨덕터에서 전하 전송의 기본을 연구하는 것 외에 양자점 접점은 매우 민감한 전하 검출기로 사용할 수 있습니다.접점을 통한 전도도는 협착의 크기에 따라 크게 달라지기 때문에 주변의 모든 잠재적 변동(예를 들어 다른 전자에 의해 생성됨)은 QPC를 통한 전류에 영향을 미칩니다.이러한 방법으로 단일 전자를 검출할 수 있다.솔리드 스테이트 시스템에서의 양자 계산의 관점에서 QPC는 양자 비트(큐비트)^[10]^[11]^[12]^[13] 상태의 읽기 디바이스로서 사용할 수 있다.디바이스 물리학에서 QPC의 구성은 완전탄도 전계효과 트랜지스터를 ^[14]시연하기 위해 사용된다.이 디바이스의 또 다른 용도는 스위치로 사용하는 것입니다.니켈 와이어를 금면에 충분히 근접시킨 후 압전 액튜에이터를 사용하여 와이어와 표면의 거리를 변경할 수 있으므로 전자 터널링과 ^[15]탄도 사이에서 디바이스의 반송 특성이 변화한다.

레퍼런스

^ H. van Houten & C.W.J. Beenakker (1996). "Quantum point contacts". Physics Today. 49 (7): 22–27. arXiv:cond-mat/0512609. Bibcode:1996PhT....49g..22V. doi:10.1063/1.881503.
^ B.J. van Wees; et al. (1988). "Quantized conductance of point contacts in a two-dimensional electron gas". Physical Review Letters. 60 (9): 848–850. Bibcode:1988PhRvL..60..848V. doi:10.1103/PhysRevLett.60.848. hdl:1887/3316. PMID 10038668.
^ D.A. Wharam; et al. (1988). "One-dimensional transport and the quantization of the ballistic resistance". J. Phys. C. 21 (8): L209–L214. Bibcode:1988JPhC...21L.209W. doi:10.1088/0022-3719/21/8/002. S2CID 45112904.
^ C.C.Dean and M. Pepper (1982). "The transition from two- to one-dimensional electronic transport in narrow silicon accumulation layers". J. Phys. C. 15 (36): L1287–L1297. Bibcode:1982JPhC...15.1287D. doi:10.1088/0022-3719/15/36/005.
^ T. J. Thornton; et al. (1986). "One-Dimensional Conduction in the 2D Electron Gas of a GaAs-AlGaAs Heterojunction". Physical Review Letters. 56 (11): 1198–1201. Bibcode:1986PhRvL..56.1198T. doi:10.1103/PhysRevLett.56.1198. PMID 10032595.
^ K-F. Berggren; et al. (1986). "Magnetic Depopulation of 1D Subbands in a Narrow 2D Electron Gas in a GaAs:AlGaAs Heterojunction". Physical Review Letters. 57 (14): 1769–1772. Bibcode:1986PhRvL..57.1769B. doi:10.1103/PhysRevLett.57.1769. PMID 10033540.
^ Pearsall, Thomas (2020). Quantum Photonics, 2nd edition. Graduate Texts in Physics. Springer. doi:10.1007/978-3-030-47325-9. ISBN 978-3-030-47324-2.
^ C.W.J.Beenakker and H. van Houten (1991). "Quantum Transport in Semiconductor Nanostructures". Solid State Physics. 44: 1–228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. doi:10.1016/s0081-1947(08)60091-0. ISBN 9780126077445. S2CID 119082619.
^ C.W.J.Beenakker and H. van Houten (1991). "Quantum Transport in Semiconductor Nanostructures". Solid State Physics. 44: 1–228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. doi:10.1016/s0081-1947(08)60091-0. ISBN 9780126077445. S2CID 119082619.
^ J.M. Elzerman; et al. (2003). "Few-electron quantum dot circuit with integrated charge read out". Physical Review B. 67 (16): 161308. arXiv:cond-mat/0212489. Bibcode:2003PhRvB..67p1308E. doi:10.1103/PhysRevB.67.161308. S2CID 16278460.
^ M. Field; et al. (1993). "Measurements of Coulomb blockade with a noninvasive voltage probe". Physical Review Letters. 70 (9): 1311–1314. Bibcode:1993PhRvL..70.1311F. doi:10.1103/PhysRevLett.70.1311. PMID 10054344.
^ J. M. Elzerman; et al. (2004). "Single-shot read-out of an individual electron spin in a quantum dot". Nature. 430 (6998): 431–435. arXiv:cond-mat/0411232. Bibcode:2004Natur.430..431E. doi:10.1038/nature02693. PMID 15269762. S2CID 4374126.
^ J. R. Petta; et al. (2005). "Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots". Science. 309 (5744): 2180–2184. Bibcode:2005Sci...309.2180P. doi:10.1126/science.1116955. PMID 16141370. S2CID 9107033.
^ E. Gremion; D. Niepce; A. Cavanna; U. Gennser & Y. Jin (2010). "Evidence of a fully ballistic one-dimensional field-effect transistor: Experiment and simulation". Applied Physics Letters. 97 (23): 233505. Bibcode:2010ApPhL..97w3505G. doi:10.1063/1.3521466.
^ Smith, D. P. E. (1995). "Quantum Point Contact Switches". Science. 269 (5222): 371–3. Bibcode:1995Sci...269..371S. doi:10.1126/science.269.5222.371. PMID 17841257. S2CID 2239813. Retrieved 30 May 2020.

추가 정보

C.W.J.Beenakker and H. van Houten (1991). "Quantum Transport in Semiconductor Nanostructures". Solid State Physics. 44: 1–228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. doi:10.1016/s0081-1947(08)60091-0. ISBN 9780126077445. S2CID 119082619.
K. J. Thomas; et al. (1996). "Possible spin polarization in a one-dimensional electron gas". Physical Review Letters. 77 (1): 135–138. arXiv:cond-mat/9606004. Bibcode:1996PhRvL..77..135T. doi:10.1103/PhysRevLett.77.135. PMID 10061790. S2CID 8903637.
Nicolás Agraït; Alfredo Levy Yeyati; Jan M. van Ruitenbeek (2003). "Quantum properties of atomic-sized conductors". Physics Reports. 377 (2–3): 81. arXiv:cond-mat/0208239. Bibcode:2003PhR...377...81A. doi:10.1016/S0370-1573(02)00633-6. S2CID 119409385.
Timp, G. (1992). "Chapter 3: When Does a Wire Become an Electron Waveguide". Semiconductors and Semimetals Volume 35. Semiconductors and Semimetals. Vol. 35. pp. 113–190. doi:10.1016/S0080-8784(08)62393-5. ISBN 9780127521350.

[1] H. van Houten & C.W.J. Beenakker (1996). "Quantum point contacts". Physics Today. 49 (7): 22–27. arXiv:cond-mat/0512609. Bibcode:1996PhT....49g..22V. doi:10.1063/1.881503.

[2] B.J. van Wees; et al. (1988). "Quantized conductance of point contacts in a two-dimensional electron gas". Physical Review Letters. 60 (9): 848–850. Bibcode:1988PhRvL..60..848V. doi:10.1103/PhysRevLett.60.848. hdl:1887/3316. PMID 10038668.

[3] D.A. Wharam; et al. (1988). "One-dimensional transport and the quantization of the ballistic resistance". J. Phys. C. 21 (8): L209–L214. Bibcode:1988JPhC...21L.209W. doi:10.1088/0022-3719/21/8/002. S2CID 45112904.

[4] C.C.Dean and M. Pepper (1982). "The transition from two- to one-dimensional electronic transport in narrow silicon accumulation layers". J. Phys. C. 15 (36): L1287–L1297. Bibcode:1982JPhC...15.1287D. doi:10.1088/0022-3719/15/36/005.

[5] T. J. Thornton; et al. (1986). "One-Dimensional Conduction in the 2D Electron Gas of a GaAs-AlGaAs Heterojunction". Physical Review Letters. 56 (11): 1198–1201. Bibcode:1986PhRvL..56.1198T. doi:10.1103/PhysRevLett.56.1198. PMID 10032595.

[6] K-F. Berggren; et al. (1986). "Magnetic Depopulation of 1D Subbands in a Narrow 2D Electron Gas in a GaAs:AlGaAs Heterojunction". Physical Review Letters. 57 (14): 1769–1772. Bibcode:1986PhRvL..57.1769B. doi:10.1103/PhysRevLett.57.1769. PMID 10033540.

[pears2-7] Pearsall, Thomas (2020). Quantum Photonics, 2nd edition. Graduate Texts in Physics. Springer. doi:10.1007/978-3-030-47325-9. ISBN 978-3-030-47324-2.

[8] C.W.J.Beenakker and H. van Houten (1991). "Quantum Transport in Semiconductor Nanostructures". Solid State Physics. 44: 1–228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. doi:10.1016/s0081-1947(08)60091-0. ISBN 9780126077445. S2CID 119082619.

[9] C.W.J.Beenakker and H. van Houten (1991). "Quantum Transport in Semiconductor Nanostructures". Solid State Physics. 44: 1–228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. doi:10.1016/s0081-1947(08)60091-0. ISBN 9780126077445. S2CID 119082619.

[10] J.M. Elzerman; et al. (2003). "Few-electron quantum dot circuit with integrated charge read out". Physical Review B. 67 (16): 161308. arXiv:cond-mat/0212489. Bibcode:2003PhRvB..67p1308E. doi:10.1103/PhysRevB.67.161308. S2CID 16278460.

[11] M. Field; et al. (1993). "Measurements of Coulomb blockade with a noninvasive voltage probe". Physical Review Letters. 70 (9): 1311–1314. Bibcode:1993PhRvL..70.1311F. doi:10.1103/PhysRevLett.70.1311. PMID 10054344.

[12] J. M. Elzerman; et al. (2004). "Single-shot read-out of an individual electron spin in a quantum dot". Nature. 430 (6998): 431–435. arXiv:cond-mat/0411232. Bibcode:2004Natur.430..431E. doi:10.1038/nature02693. PMID 15269762. S2CID 4374126.

[13] J. R. Petta; et al. (2005). "Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots". Science. 309 (5744): 2180–2184. Bibcode:2005Sci...309.2180P. doi:10.1126/science.1116955. PMID 16141370. S2CID 9107033.

[14] E. Gremion; D. Niepce; A. Cavanna; U. Gennser & Y. Jin (2010). "Evidence of a fully ballistic one-dimensional field-effect transistor: Experiment and simulation". Applied Physics Letters. 97 (23): 233505. Bibcode:2010ApPhL..97w3505G. doi:10.1063/1.3521466.

[switches-15] Smith, D. P. E. (1995). "Quantum Point Contact Switches". Science. 269 (5222): 371–3. Bibcode:1995Sci...269..371S. doi:10.1126/science.269.5222.371. PMID 17841257. S2CID 2239813. Retrieved 30 May 2020.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Search

양자점 접점

네임스페이스

더

목차

제조

특성.

적용들

레퍼런스

추가 정보