단사정계

결정학에서 단사정계는 7개의 결정계 중 하나입니다.결정계는 3개의 벡터로 설명됩니다.단사정계에서 결정은 사방정계에서처럼 길이가 동일하지 않은 벡터로 설명됩니다.그들은 평행사변 프리즘을 형성합니다.따라서 두 쌍의 벡터는 수직이고(직각에서 만나다), 세 번째 쌍은 90°가 아닌 다른 각도를 만듭니다.

브라베 격자

두 개의 단사정계 브라베 격자가 존재합니다: 원시 단사정계와 염기 중심 단사정계.

브라베 격자	원시적인 단사정계의	베이스 중심의 단사정계의
피어슨 기호	mP	씨
단위전지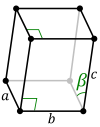

베이스 중심 단사정계 격자의 경우, 원시 셀은 비스듬한 마름모 프리즘 형상을 가지며,^[1] 2차원 중심 사각형 베이스 층은 원시 마름모 축으로도 설명할 수 있기 때문에 제작이 가능함.아래 프리미티브 셀의 $a$ a $a$ 는 ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ 2 ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ + ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ ${\$ }}{2}}와 같습니다. $}}}}$ 위의 통상적인 $셀$ 의 ${\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}$ .

비스듬한 마름모 프리즘 원시 세포

기저중심 단사정계 격자의 원시 세포

원시 세포와 기존 세포의 기저층간의 관계

크리스탈 클래스

아래 표는 단사정계 결정계의 공간군을 결정급별로 정리한 것입니다.이 표에는 결정학 공간군 번호 다음으로 결정학 공간군 번호, ^[2]쇤플라이 표기법의 점군, 헤르만-마우귄 표기법, 오비폴드 표기법, 콕서터 표기법, 활자 기술자, 광물 예시 및 공간군 표기법이 나열되어 있습니다.

#	점군					유형	예	스페이스 그룹
#	이름^[3]	쇤.	인터내셔널	오브.	콕스.	유형	예	원시적인	베이스 중심의
3–5	구불구불한	다₂	2	22	[2]⁺	반동형의 북극의	할로트리카이트	P2, P2₁	C2
6–9	도마틱	C_s(C_1h)	m	*11	[ ]	북극의	고지식한	Pm, Pc	Cm, Cc
10–12	각기둥	다_2h	2/m	2*	[2,2⁺]	중심대칭의	석고	P2/m, P2₁/m	C2/m
13–15	각기둥	다_2h	2/m	2*	[2,2⁺]	중심대칭의	석고	P2/c, P2₁/c	C2/c

스페노이드는 단사정계 헤미모픽, 도마틱은 단사정계 헤미모픽, 각형은 단사정계 노멀, 각형은 단사정계는 단사정계 노멀이라고도 합니다.

세 개의 단사정계 헤미모픽 공간군은 다음과 같습니다.

벽지 그룹 p2 단면의 프리즘
축 대신 나사 축을 사용하여 dito
나사 축과 축 사이에 병렬로 있는 ditto; 이 경우 추가 변환 벡터는 기본 평면에 있는 변환 벡터의 반과 기본 평면 사이에 있는 수직 벡터의 반입니다.

네 개의 단사정계 반면체 공간군은 다음을 포함합니다.

그 프리즘의 밑부분과 중간부분에 순수한 반사를 하는 사람들.
순수 반사면 대신 활공면을 갖는 것들; 활공면은 기본면에서 병진 벡터의 반이다.
서로 사이에 있는 것들; 이 경우에 추가적인 병진 벡터는 이 활공에 기본 평면 사이에 있는 수직 벡터의 반을 더한 것입니다.

2차원으로

2차원에서 유일한 단사정계 브라베 격자는 비스듬한 격자입니다.

브라베 격자	비스듬히
피어슨 기호	mp
단위전지

참고 항목

참고문헌

^ Hahn (2002), p. 746, 행 mC, 열 프리미티브 참조. 여기서 셀 파라미터는 a1 = a2, α = β로 주어집니다.
^ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. S2CID 146060934.
^ "The 32 crystal classes". Retrieved 2018-06-19.

추가열람

Hurlbut, Cornelius S.; Klein, Cornels (1985). Manual of Mineralogy (20th ed.). pp. 69–73. ISBN 0-471-80580-7.
Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. Vol. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.

[1] Hahn (2002), p. 746, 행 mC, 열 프리미티브 참조. 여기서 셀 파라미터는 a1 = a2, α = β로 주어집니다.

[ITC-2] Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. S2CID 146060934.

[3] "The 32 crystal classes". Retrieved 2018-06-19.

[1]

[2]

[3]

v t 크리스털 시스템
브라베 격자 결정형 점군
7개의 3D 시스템	삼사정통의 단사정계의 오르소 옴의 정방정계의 삼각형 & 육각형 입방체 (등각)
4개의 2D 시스템	비스듬한 직사각형의 광장 육각형의

Search