최대 동력 전달 정리

전기 공학에서, 최대 동력 전달 정리는 유한한 내부 저항을 가진 선원에서 최대 외부 전력을 얻으려면, 하중의 저항은 출력 단자에서 본 선원의 저항과 같아야 한다고 기술하고 있다. 모리츠 폰 자코비는 1840년경 최대 권력(이양) 정리를 발표했는데, 이를 '자코비의 법칙'^[1]이라고도 한다.

그 정리는 회로에 걸친 최대 전력 전달을 초래하며, 최대 효율은 아니다. 부하 저항이 선원의 저항보다 커지면 효율은 더 높아지는데, 이는 선원의 높은 비율이 부하로 전달되기 때문이다. 그러나 총 회로 저항이 증가하기 때문에 부하 출력의 크기는 더 낮다.^[2]

부하 저항이 소스 저항보다 작으면, 대부분의 전력은 결국 소스에서 소진되고, 총 소산된 전력은 더 높지만, 총 저항이 더 낮기 때문에 부하에서 소산된 양이 감소하는 것으로 나타났다.

정리는 일단 소스 저항이 주어지면 부하 저항을 선택하는 방법(전력 전달을 최대화하도록)을 명시한다. 정리를 반대 시나리오에 적용하는 것은 일반적인 오해다. 주어진 부하 저항의 소스 저항을 선택하는 방법은 명시되어 있지 않다. 실제로 전압원으로부터의 전력 전달을 최대화하는 소스 저항은 부하 저항의 값에 관계없이 항상 0이다.

정리는 리액턴스를 포함하는 교류회로까지 확장할 수 있으며, 부하 임피던스가 소스 임피던스의 복잡한 결합과 같을 때 최대 전력 전달이 발생한다고 기술하고 있다.

최근의 서술문은^[2][3] 최대 권력 정리의 기초 수학이 다음과 같은 다른 물리적 상황에도 어떻게 적용되는지를 보여준다.

• mechanical collisions between two objects,
• the sharing of charge between two capacitors,
• liquid flow between two cylinders
• the transmission and reflection of light at the boundary between two media

Maximizing power transfer versus power efficiency

The theorem was originally misunderstood (notably by Joule^{[citation needed]}) to imply that a system consisting of an electric motor driven by a battery could not be more than 50% efficient since, when the impedances were matched, the power lost as heat in the battery would always be equal to the power delivered to the motor.

In 1880 this assumption was shown to be false by either Edison or his colleague Francis Robbins Upton, who realized that maximum efficiency was not the same as maximum power transfer.

To achieve maximum efficiency, the resistance of the source (whether a battery or a dynamo) could be (or should be) made as close to zero as possible. Using this new understanding, they obtained an efficiency of about 90%, and proved that the electric motor was a practical alternative to the heat engine.

The condition of maximum power transfer does not result in maximum efficiency.

If we define the efficiency η as the ratio of power dissipated by the load, R_L, to power developed by the source, V_S, then it is straightforward to calculate from the above circuit diagram that

${\displaystyle \eta ={\frac {R_{\mathrm {L} }}{R_{\mathrm {L} }+R_{\mathrm {S} }}}={\frac {1}{1+R_{\mathrm {S} }/R_{\mathrm {L} }}}.}$

Consider three particular cases:

• If ${\displaystyle R_{\mathrm {L} }=R_{\mathrm {S} }}$, then ${\displaystyle \eta =0.5,}$
• If ${\displaystyle R_{\mathrm {L} }\to \infty }$ or ${\displaystyle R_{\mathrm {S} }=0,}$ then ${\displaystyle \eta =1,}$
• If ${\displaystyle R_{\mathrm {L} }=0}$, then ${\displaystyle \eta =0.}$

The efficiency is only 50% when maximum power transfer is achieved, but approaches 100% as the load resistance approaches infinity, though the total power level tends towards zero.

Efficiency also approaches 100% if the source resistance approaches zero, and 0% if the load resistance approaches zero. In the latter case, all the power is consumed inside the source (unless the source also has no resistance), so the power dissipated in a short circuit is zero.

Impedance matching

A related concept is reflectionless impedance matching.

In radio frequency transmission lines, and other electronics, there is often a requirement to match the source impedance (at the transmitter) to the load impedance (such as an antenna) to avoid reflections in the transmission line that could overload or damage the transmitter.

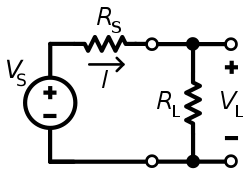
Calculus-based proof for purely resistive circuits

In the diagram opposite, power is being transferred from the source, with voltage V and fixed source resistance R_S, to a load with resistance R_L, resulting in a current I. By Ohm's law, I is simply the source voltage divided by the total circuit resistance:

${\displaystyle I={\frac {V}{R_{\mathrm {S} }+R_{\mathrm {L} }}}.}$

The power P_L dissipated in the load is the square of the current multiplied by the resistance:

${\displaystyle P_{\mathrm {L} }=I^{2}R_{\mathrm {L} }=\left({\frac {V}{R_{\mathrm {S} }+R_{\mathrm {L} }}}\right)^{2}R_{\mathrm {L} }={\frac {V^{2}}{R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}}.}$

The value of R_L for which this expression is a maximum could be calculated by differentiating it, but it is easier to calculate the value of R_L for which the denominator

${\displaystyle R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}$

is a minimum. The result will be the same in either case. Differentiating the denominator with respect to R_L:

${\displaystyle {\frac {d}{dR_{\mathrm {L} }}}\left(R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }\right)=-R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}+1.}$

For a maximum or minimum, the first derivative is zero, so

${\displaystyle R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}=1}$

or

${\displaystyle R_{\mathrm {L} }=\pm R_{\mathrm {S} }.}$

In practical resistive circuits, R_S and R_L are both positive, so the positive sign in the above is the correct solution.

To find out whether this solution is a minimum or a maximum, the denominator expression is differentiated again:

${\displaystyle {{d^{2}} \over {dR_{\mathrm {L} }^{2}}}\left({R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}\right)={2R_{\mathrm {S} }^{2}}/{R_{\mathrm {L} }^{3}}.\,\!}$

This is always positive for positive values of ${\displaystyle R_{\mathrm {S} }\,\!}$ and ${\displaystyle R_{\mathrm {L} }\,\!}$, showing that the denominator is a minimum, and the power is therefore a maximum, when

${\displaystyle R_{\mathrm {S}}}=R_{\mathrm {L}.\,\!}$

The above proof assumes fixed source resistance ${\displaystyle R_{\mathrm {S} }\,\!}$. When the source resistance can be varied, power transferred to the load can be increased by reducing ${\displaystyle R_{\textrm {S}}\,\!}$. For example, a 100 Volt source with an ${\displaystyle R_{\textrm {$$S}}\,\!}$ of ${\displaystyle 10~\Omega }$ will deliver 250 watts of power to a ${\displaystyle 10~\Omega }$ load; reducing ${\displaystyle R_{\textrm {S}}\,\!}$ to ${\displaystyle 0~\Omega }$ increases the power delivered to 1000 watts.

이는 최대 전력 전달이 부하 전압이 소스와 동등한 테베닌 전압의 1/2과 동일하다고 해석할 수 있음을 보여준다.^[4]

반응성 회로 내

동력 전달 정리는 소스 및/또는 부하가 순수하게 저항성이 없는 경우에도 적용된다.

최대 전력 정리의 개선은 소스와 하중의 모든 반응성 구성요소는 크기가 동일해야 하지만 반대 기호여야 한다고 말한다. (도출은 아래를 참조하십시오.)

• 즉, 선원과 부하 임피던스는 서로 복잡한 결합체여야 한다.
• 순전히 저항성 회로의 경우, 두 개념은 동일하다.

물리적으로 실현 가능한 선원과 부하는 일반적으로 순전히 저항성이 있는 것이 아니며, 유도성 또는 용량성 구성요소를 가지고 있으므로, 복잡한 결합 임피던스 매칭이라는 이름으로 이 정리의 실용적인 적용이 실제로 존재한다.

선원이 완전히 귀납적(용량적)인 경우, 저항성 손실이 없는 경우, 완전 용량성(유도적) 부하는 선원에서 100% 에너지를 공급받지만 1/4 사이클 후에 다시 보낸다.

결과 회로는 에너지가 계속해서 왕복으로 진동하는 공명 LC 회로에 지나지 않는다. 이 진동은 반응력이라고 불린다.

역률 보정(유도 리액턴스를 사용하여 용량성 리액턴스를 "균형화"하는 경우)은 완전히 다른 이유로 수행되지만 본질적으로 복잡한 결합 임피던스 매칭과 동일한 생각이다.

고정 반응성 선원의 경우, 최대 전력 정리는 하중을 선원에 일치시키는 복잡한 결합에 의해 하중에 전달되는 실제 전력(P)을 최대화한다.

고정된 반응 부하에 대해 동력 계수 보정은 송신선에 의해 수행되는 겉보기 전력(S) (및 불필요한 전류)을 최소화하는 동시에 동일한 양의 실제 동력 전달을 유지한다.

이것은 부하에 리액턴스를 추가하여 부하 자체의 리액턴스를 밸런싱하고, 반응 부하 임피던스를 저항 부하 임피던스로 변경함으로써 이루어진다.

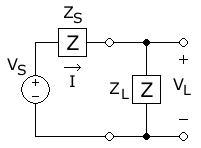
증명

이 다이어그램에서 AC 전원은 전압 ${\displaystyle V{}_{}}$ ${\displaystyle S_{}}$ $displaystyle V_{\text{$의 페이소르 진폭과 함께 소스로부터 전송되고 있다.$S}}}($양극 피크 전압) 및 고정 소스 임피던스 Z ${\displaystyle S_{}}$ ${\$$S}}($소스의 경우 S)을 $임피던스{\displaystyle {}_{}}$ ${\displaystyle Z_{}}$ L$${\$displaystyle Z_{\text}$이(가) 있는 로드까지$L}}($부하의 경우 L)을 생성하여 현재 Phasor $I{\displaystyle }$ ${\displaystyle I}$의 (양) 크기 ${\displaystyle I}$ $displaystyle$ I}을$($를) 발생$.$ 이 크기 ${\displaystyle I}$ $displaystyle I}$은 소스 전압의 크기를 총 회로 임피던스의 크기로 나눈 결과$$:

${\displaystyle I ={ V_{\text{S}} \over Z_{\text{S}}+Z_{\text{L}} }.}$

The average power ${\displaystyle P_{\text{L}}}$ dissipated in the load is the square of the current multiplied by the resistive portion (the real part) ${\displaystyle R_{\text{L}}}$ of the load impedance ${\displaystyle Z_{\text{L}}}$:

${\displaystyle {\begin{aligned}P_{\text{L}}&=I_{\text{rms}}^{2}R_{\text{L}}={1 \over 2} I ^{2}R_{\text{L}}\\&={1 \over 2}\left({ V_{\text{S}} \over Z_{\text{S}}+Z_{\text{L}} }\right)^{2}R_{\text{L}}={1 \over 2}{ V_{\text{S}} ^{2}R_{\text{L}} \over (R_{\text{S}}+R_{\text{L}})^{2}+(X_{\text{S}}+X_{\text{L}})^{2}},\end{aligned}}}$

where ${\displaystyle R_{\text{S}}}$ and ${\displaystyle R_{\text{L}}}$ denote the resistances, that is the real parts, and ${\displaystyle X_{\text{S}}}$ and ${\displaystyle X_{\text{L}}}$ denote the reactances, that is the imaginary parts, of respectively the source and load impedances ${\displaystyle Z_{\text{S}}}$ and ${\displaystyle Z_{\text{L}}}$.

To determine, for a given source voltage ${\displaystyle V_{\text{S}}}$ and impedance ${\displaystyle Z_{\text{S}},}$ the value of the load impedance ${\displaystyle Z_{\text{L}},}$ for which this expression for the power yields a maximum, one first finds, for each fixed positive value of ${\displaystyle R_{\text{L}}}$, the value of the reactive term ${\displaystyle X_{\text{L}}}$ for which the denominator

${\displaystyle(R_{\text{S}+R_{\text{L}}^{2}+(X_{\text{S}+X_{\text{L}}^{2}\,}$

최소값이다. 리액턴스는 음수일 수 있으므로, 부하 리액턴스를 에 적응시킴으로써 달성된다.

${\displaystyle X_{\text{L}}=-X_{\text{S}}.}$

이는 위의 방정식을 다음과 같이 감소시킨다.

${\displaystyle P_{\text{L}}={\frac {1}{1}:{2}}: {\frac {V_{\text}{S} ^{2}R_{\text{L}}{(R_{\text{S}+R_{\text{L}}^{2}}:}$

${\displaystyle R_{}}$L ${\${$이$ 표현을 극대화하는 L$}}.$ 이 문제는 순전히 저항성 사례에서와 같은 형태를 가지며, 따라서 최대화 $조건$은 ${\displaystyle R_{}}$L = ${\displaystyle R_{}}$S .$${\$displaystyle R_{\$text{\$text}$이다.$L}}=R_{\text{$$S}}.}$

두 가지 최대화 조건

• ${\displaystyle R_{\text{L}}=R_{\text{S}}$
• ${\displaystyle X_{\text{L}}=-X_{\text{S}}$

impedance${\displaystyle {}^{}}$, {\$displaystyle ^{*}}$로 표시된 소스 임피던스의 복잡한 결합을 설명하여$$ 다음과 같이 간결하게 결합할 수 있다.

${\displaystyle Z_{\text{L}}=Z_{\text{S}}^{*}.}$

메모들

참조

• H.W. 잭슨(1959) 전자회로 소개, 프렌티스 홀.

외부 링크

• 전자파 및 안테나에서 추출한 공극 매칭 대 반사 없는 매칭(PDF)
• 스파크 송신기 2. 최대 전력, 파트 1